Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


178
Chapter
5.
Boundary
value
problems
in
statics
just below (5.38), using integration
by
parts. Indeed,
the
simplest
way of
deriving
the
weak
form
is to
start
with
the
differential
equation
multiply
by an
arbitrary "test function"
v
e
V to get
and
then integrate both sides
from
0 to
i:
Integrating
by
parts
on the
left
and
applying
the
boundary conditions yield
the
weak
form.
Now
suppose
u
satisfies (5.40),
the
weak
form
of the
BVP. Then,
by
definition
of
V,
w(0)
=
u(i]
= 0. We now use
integration
by
parts
to
show
that
u
satisfies
the
strong
form
of the
differential
equation.
We
have
The
boundary terms vanish because
of the
boundary conditions
v(Qi)
=
v(i]
= 0.
We
have
This condition
can
only
be
true
if
on the
interval
[0,
i].
The
proof
is
simple, given
the
following
fact:
If 0 < c < d <
I,
then
there
exists
a
function
V[
c
^]
£
V
such
that
v^
c
^(x)
> 0 for all x €
(c,d)
and
v
[c,d](
x
)
=
0 for all x in
[0,c]
or
[d,i\.
(Exercise
3
asks
the
reader
to
construct such
a
function
v\
c
&.}
If
178
Chapter
5.
Boundary value problems
in
statics
just
below (5.38), using integration by parts. Indeed,
the
simplest way of deriving
the
weak form
is
to
start
with the differential equation
d (
du
)
-
dx
k(x)
dx
(x) =
f(x),
0 < x < f,
multiply by
an
arbitrary
"test function" v E V
to
get
d (
du
)
-
dx
k(x)
dx
(x) v(x) = f(x)v(x), 0 < x < f,
and
then
integrate
both
sides from 0 to f:
{l d (
dU)
(l
-
10
dx
k(x)
dx
(x) v(x)
dx
=
10
f(x)v(x)
dx.
Integrating by
parts
on the left
and
applying the boundary conditions yield the
weak form.
Now suppose
U satisfies (5.40),
the
weak form of the BVP. Then, by definition
of
V,
u(O)
= u(f) =
O.
We
now use integration by
parts
to
show
that
u satisfies the
strong form of
the
differential equation.
We
have
{i
du
dv
(l
10
k(x)
dx
(x)
dx
(x)
dx
-
10
f(x)v(x)
dx
= 0 for all v E V
[
dU
] i
(-
d (
du
)
=>
k(x)dx(x)v(x) 0 -
10
dx
k(x)
dx
(x) v(x)dx
-
foi
f(x)v(x)
dx
= 0 for all v E V
=>-
foi
{d~
(k(X)~~(x))
+f(X)}V(X)dx=oforallvEv.
The boundary terms vanish because of the boundary conditions
v(O)
= v(f) =
O.
We
have
fol
{d~
(k(X)
~~
(X)) +
f(X)}
v(x)
dx
= 0 for all v E
V.
(5.41)
This condition can only be
true
if
d (
du
)
dx
k(x)
dx
(x) +
f(x)
= 0
(5.42)
on the interval
[0,
fl. The proof
is
simple, given the following fact:
If
0 < e < d <
f,
then
there exists a function
V[c,dj
E V such
that
V[c,dj(X)
> 0 for all x E
(e,d)
and
V[c,dj(x)
= 0 for all x in
[O,e]
or
[d,f]. (Exercise 3 asks the reader
to
construct such
a function
V[c,dj.)
If
d (
du
)
dx
k(x)dx(x)
+f(x)

cannot
be
positive
on any
small interval.
By the
same reasoning,
it
cannot
be
negative
on any
small interval.
It
follows
that
(5.42)
must hold.
Thus,
to
solve (5.39),
it
suffices
to
solve
the
weak
form
(5.40).
The
weak
form
consists
of
infinitely
many equations, since there
are
infinitely
many
"test
functions"
v £
V.
The
original
PDE
also implies
an
infinite number
of
equations, since
the
equation must hold
for
each
of the
infinitely many values
of x £ [0,
i\.
In
either case,
we
cannot
find the
solution directly, since
any
practical computational procedure
must reduce
to a finite
number
of
steps.
The
weak
form
admits
the use of the
Galerkin
method, which reduces
the
infinitely
many equations
to a finite
collection
of
equations whose solution provides
an
approximate solution
to the
BVP.
Exercises
1.
Show
that
the
differential
operator
defined
by
is
symmetric:
2.
Suppose
that
k(x)
> 0 for all x £
[0,1].
Show
that
if the
operator
K,
defined
in
the
previous exercise,
has an
eigenvalue, then
it
must
be
positive. (Hint:
Let
A
be an
eigenvalue
and
u
a
corresponding
eigenfunction.
Compute
(Ku,u)
two
ways, once using
the
fact
that
u is an
eigenfunction
and
again using
integration
by
parts
once.)
3. Let 0 < c < d < t
hold. Find
a
function
V[
CJ(
Q
that
is
twice-continuously
differentiate
on [0,
i]
and
satisfies
the
conditions
that
5.4.
Finite
element methods
for
BVPs
179
were
positive
on a
small interval
[c, d] C
[0,£],
then
would
be
positive
on [c,
d\
and
zero
on the
rest
of [0,
^],
and
hence
would
be
positive. Since this integral
is
zero
for all v £
V,
this shows
that
5.4.
Finite element methods for BVPs 179
were positive
on
a small interval
[c,
d]
C
[0,
£],
then
would
be
positive
on
[c,
d]
and
zero on
the
rest
of
[0,
£],
and
hence
would
be
positive. Since this integral is zero for all v E
V,
this
shows
that
d (
du
)
dx
k(x)dx(x) +f(x)
cannot
be
positive
on
any
small interval.
By
the
same
reasoning,
it
cannot
be
negative
on
any
small interval.
It
follows
that
(5.42)
must
hold.
Thus,
to
solve (5.39),
it
suffices
to
solve
the
weak form (5.40).
The
weak form
consists of infinitely
many
equations, since
there
are
infinitely
many
"test
functions"
v E V.
The
original
PDE
also implies
an
infinite
number
of
equations, since
the
equation
must
hold for each of
the
infinitely
many
values
of
x E
[0,
fl.
In
either case,
we
cannot
find
the
solution directly, since
any
practical
computational
procedure
must
reduce
to
a finite
number
of steps.
The
weak form
admits
the
use of
the
Galerkin
method,
which reduces
the
infinitely
many
equations
to
a finite collection
of equations whose solution provides
an
approximate
solution
to
the
BVP.
Exercises
1. Show
that
the
differential
operator
K :
c1
[0,
£]
-+
C[O,
f]
defined by
Ku
=
--
k(x)-
d (
dU)
dx
dx
is
symmetric:
(Ku,v) = (u,Kv) for all
U,V
E
C1[0,£].
2.
Suppose
that
k(x) > ° for all x E
[0,
fl.
Show
that
if
the
operator
K,
defined in
the
previous exercise, has
an
eigenvalue,
then
it
must
be positive. (Hint: Let
A
be
an
eigenvalue
and
u a corresponding eigenfunction.
Compute
(K
u, u)
two ways, once using
the
fact
that
u
is
an
eigenfunction
and
again using
integration
by
parts
once.)
3. Let
° < c < d < £ hold.
Find
a function V[c,d]
that
is
twice-continuously
differentiable on
[0,
£]
and
satisfies
the
conditions
that
V[c,dJ(X) > ° for all x E
(c,
d)

180
Chapter
5.
Boundary value problems
in
statics
The
function
is
called bilinear because, holding
one
argument
fixed, the
function
is
linear
in the
other:
and
Hint:
Let
p(x]
be a
polynomial such
that
Then
define
4.
Show
that
both
of the
integrals
have units
of
energy
(force
times distance).
5.
Consider
the
damped wave equation
where
c > 0 is a
constant.
By
modifying
the
calculation beginning
on
page
173, show
that
the
total
energy (kinetic energy plus elastic potential energy)
is
decreasing
with time.
5.5 The
Galerkin
method
As
we
stated
earlier,
the
Galerkin method
defines
an
approximate solution
to the
weak
form
of the BVP by
restricting
the
problem
to a finite-dimensional
subspace.
This
has the
effect
of
reducing
the
infinitely
many equations contained
in
(5.40)
to
a finite
system
of
equations.
To
describe
the
Galerkin method,
it is
convenient
to
introduce
the
following
notation.
We
define
the
symmetric
bilinear
form
a(-,
•) by
180
Chapter
5.
Boundary value problems
in
statics
and
V[c,d](X) = ° for all x E
[0,
c]
U
[d,
fl.
Hint: Let p(x) be a polynomial such
that
dp
d
2
p
dp
~p
p(c)
=
dx
(c)
=
dx
2
(c)
= 0, p(d) =
dx
(d)
=
dx
2
(d)
=
o.
Then
define
()
{P(X),
c<x<d,
V[c,d] x =
0,
0
~
x
~
c or d
~
x
~
£.
4. Show
that
both
of
the
integrals
1 r
f
(a
) 2 1 r
f
(a
) 2
"210
Ap(x)
a~
dX'"2
10
Ak(x)
a:
dx
have units of energy (force times distance).
5.
Consider
the
damped wave equation
a
2
u au a (
au)
Ap(x)
at
2
+ c at - A ax k(x) ax =
0,
0 < x < f,
t>
0,
u(O,
t) =
0,
t >
0,
u(f,t)
=
0,
t >
0,
where c > 0 is a constant. By modifying
the
calculation beginning on page
173, show
that
the
total
energy (kinetic energy plus elastic potential energy)
is decreasing with time.
5.5 The Galerkin method
As
we
stated
earlier,
the
Galerkin method defines
an
approximate solution
to
the
weak form of
the
BVP
by restricting
the
problem
to
a finite-dimensional subspace.
This has
the
effect of reducing the infinitely many equations contained in (5.40)
to
a finite system of equations. To describe the Galerkin method,
it
is convenient
to
introduce
the
following notation. We define
the
symmetric bilinear form
a(·,·)
by
r
f
du
dv
a(u,v) =
10
k(x)dx(x)dx(x)dx.
The
function is called bilinear because, holding one argument fixed,
the
function is
linear in
the
other:
a(alul
+a2U2,V) = ala(Ul,V) +a2a(u2,V) for all
al,a2
E
R,
Ul,U2,V,
a(u,
al
Vl
+
a2v2)
= ala(u,
Vl)
+ a2a(u,
V2)
for all
al,
a2 E
R,
U,
Vl,
V2.

Below
we
show
that
(5.44)
has a
unique solution
that
can be
found
by
solving
a
matrix-vector
equation
(that
is, a
system
of
linear algebraic equations).
First
we
show
that
solving
(5.44)
is
useful:
the
Galerkin
approximation
is the
best
approxi-
mation, from
V
n
,
to the
true solution.
5.5.
The
Galerkin
method
181
The
bilinear
form
is
called symmetric because
Bilinearity
and
symmetry
are two of the
properties
of an
inner product (see Section
3.4).
The
third property also holds
if we
restrict
a(-,
•) to
vectors
in V =
Cf^O,^]:
and
From
the
definition
of
a(-,
•), we
have
The
Galerkin idea
is
simple. Choose
a finite-dimensional
subspace
V
n
of V, and
reduce (5.43)
to the
subspace:
where
(-,
•) is the
L
2
inner product. Thus,
the
weak
form
(5.40)
of the
model
BVP
(5.39)
can be
written
as
where
C is a
constant.
But we
already know
that
w(0)
= 0 and u is
continuous
on
[0,1].
Therefore,
C
must
be
zero, which
is
what
we
wanted
to
prove. Thus
o(-,
•)
defines
an
inner product
on
V.
We
recall
that
Since
the
integrand
is
nonnegative,
we
clearly have
a(u,
u)
>
0 for all
u.
Moreover,
the
integral
of a
nonnegative
function
can
only
be
zero when
the
function
(the
integrand)
is the
zero function. Thus,
5.5.
The
Galerkin
method
181
The
bilinear form is called symmetric because
a(u,v) = a(v,u) for all u,V.
Bilinearity
and
symmetry are two
of
the
properties
of
an
inner
product
(see Section
3.4).
The
third
property
also holds if
we
restrict a(·,·)
to
vectors in V = Cb[O,f]:
a(
u,
u)
~
0 for all u E V
and
a(u,u) > 0 for all u E
V,U
i-
O.
From
the
definition of a(·, .),
we
have
a(u,u) =
1£
k(x)
(~~(X)r
dx.
Since
the
integrand is nonnegative,
we
clearly have
a(
u,
u)
~
0 for all
u.
Moreover,
the
integral of a nonnegative function can only
be
zero when
the
function (the
integrand) is
the
zero function. Thus,
a(u,U)=0=?k(X)(~~(X))2
=0,
O<x<f,
=?
~~
(x) = 0, 0 < x < f (since
k(x)
> 0),
=? u(x) =
C,
0 < x < f,
where C is a constant.
But
we
already know
that
u(O)
= 0
and
u
is
continuous
on
[O,f].
Therefore, C must
be
zero, which
is
what
we
wanted
to
prove.
Thus
a(·,·)
defines
an
inner product
on
V.
We
recall
that
11
f(x)v(x)
dx =
(f,v),
where (.,.) is
the
L2
inner product. Thus,
the
weak form (5.40) of
the
model
BVP
(5.39) can
be
written as
find u E V satisfying a(u,
v)
=
(f,
v)
for all v E
V.
(5.43)
The
Galerkin idea is simple. Choose a finite-dimensional subspace
Vn
of V,
and
reduce (5.43)
to
the
subspace:
find
Vn
E
Vn
satisfying a(vn,V) =
(f,v)
for all v E V
n
.
(5.44)
Below
we
show
that
(5.44) has a unique solution
that
can
be
found by solving a
matrix-vector equation
(that
is, a system
of
linear algebraic equations).
First
we
show
that
solving (5.44) is useful: the Galerkin approximation is the best approxi-
mation, from V
n
, to the true solution.

182
Chapter
5.
Boundary
value
problems
in
statics
Suppose
u 6 V is the
solution
to
(5.43),
V
n
is a finite-dimensional
subspace
of
V,
and
v
n
e
V
n
is the
solution
to
(5.44). Then
we
have
Subtracting
the
second equation
from
the first, we see
that
or,
using
the
bilinearity
of
a(-,-),
Since
o(-,
•)
defines
an
inner product
on V, the
projection theorem (see Theorem
3.36
in
Section 3.4) shows
that
v
n
is the
best approximation
to u
from
V
n
,
when
"best"
is
defined
by the
norm induced
by
o(-,
•):
where
We
usually
refer
to || • \\E as the
energy
norm
and to
«(-,-)
as the
energy
inner
product.
To
compute
v
n
,
suppose
{</>i,02,
• • •
,^n}
is a
basis
for
V
n
.
Then (5.44)
is
equivalent
to
Since
v
n
belongs
to
V
n
,
it can be
written
as a
linear combination
of the
basis vectors:
(We
now
have
two
meanings
for the
symbol "u."
The
function
u is the
exact
solution
to the
BVP, while
the
components
of the
vector
u are the
weights
in the
representation
of the
approximation
v
n
in
terms
of the
basis
0i,
02,
• •
•,
(f>
n
-
We
will
live
with this ambiguity
in
order
to
adhere
to
standard
notation.)
Finding
v
n
is now
equivalent
to
determining
HI,
1*2,...,
u
n
.
Substituting (5.46)
into
(5.45)
yields
or,
using
the
bilinearity
of
o(-,
•),
182
Chapter
5. Boundary value problems
in
statics
Suppose U E V
is
the
solution
to
(5.43),
Vn
is a finite-dimensional subspace of
V,
and
Vn
E
Vn
is
the
solution
to
(5.44).
Then
we
have
UEV,
a(u,v) =
(f,v)
forallvEV,
vnEV
n
, a(vn,v)
=
(f,v)
forallvEV
n
·
Subtracting
the
second equation from
the
first,
we
see
that
a(u,v) - a(vn,v) = 0 for all v E
Vn
or, using
the
bilinearity of a(·, .),
a(u - vn,v) = 0 for all v E V
n
.
Since a(·,·) defines
an
inner product on V,
the
projection theorem (see Theorem
3.36 in Section 3.4) shows
that
Vn
is
the
best approximation
to
u from V
n
, when
"best"
is
defined by
the
norm induced by a(·,
.):
Ilu
-
vnllE
:::;
Ilu
-
wilE
for all w E V
n
,
where
IlvIIE=va(v,v)=
1\(X)(~~(X))2
dx
forallvEV.
We usually refer
to
II
.
liE
as the energy norm
and
to
a(·,·) as
the
energy inner
product.
To compute V
n
, suppose
{(/>1,
¢2,
...
, ¢n} is a basis for V
n
. Then (5.44) is
equivalent
to
find
Vn
E
Vn
satisfying a(vn,¢i) =
(f,¢i),i
= 1,2,
...
,n.
(5.45)
Since
Vn
belongs
to
V
n
,
it
can be written as a linear combination of
the
basis vectors:
n
Vn
=
I:
Uj¢j'
j=l
(5.46)
(We
now have two meanings for
the
symbol "u."
The
function u is
the
exact
solution
to
the
BVP, while
the
components of
the
vector u are
the
weights in
the
representation of
the
approximation
Vn
in terms
of
the
basis
¢l,
¢2,
...
, ¢n'
We
will
live with this ambiguity in order
to
adhere
to
standard
notation.)
Finding
Vn
is
now equivalent
to
determining
Ul,
U2,
.
..
,
Un.
Substituting (5.46)
into (5.45) yields
or, using
the
bilinearity of a(·, .),
n
I:a(¢j,¢i)Uj
=
(f,¢i),
i = 1,2,
...
,n.
j=l

5.5.
The
Galerkin
method
183
This
is a
system
of n
linear
equations
for the
unknowns
wi,
U2,
• •
•,
u
n
.
We
define
a
matrix
K €
R
nxn
and a
vector
f
e
R
n
by
(We
now
also have
two
meanings
for the
symbol
"f":
the
function
/ is the
right-hand
side
of the
differential
equation, while
the
vector
f has
components
fi —
(/,&).}
Finding
v
n
is now
equivalent
to
solving
the
linear system
The
matrix
K is
usually called
the
stiffness
matrix, since, when applied
to
problems
in
mechanics,
the
entries
in K
depend
on the
stiffness
k(x)
of the
material.
For
analogous reasons,
the
vector
f is
usually called
the
load
vector.
31
The
reader will recall
that,
in
computing
a
best approximation,
it is
advan-
tageous
to
have
an
orthogonal basis, since then
the
stiffness
(or
Gram) matrix
is
diagonal,
and the
projection
is
computed
by n
inner products. However,
the
basis
for
V
n
must
be
orthogonal with respect
to the
energy inner product,
and
with
a
nonconstant
coefficient
k(x),
it is
usually
difficult
32
to find an
orthogonal
basis.
Therefore,
in the finite
element method,
we
will
use a
nonorthogonal basis.
We
now
illustrate
the
Galerkin method
by
applying
it to two
BVPs,
one
with
constant
coefficients
and the
other with nonconstant
coefficients.
Example
5.18.
Let FN be the
subspace
ofV
spanned
by the
basis
This
basis
is
orthogonal with
respect
to the
ordinary
L
2
inner product
on the
interval
[0,1].
Consider
the BVP
(this
is
(5.39)
with
k(x)
=
I).
The
exact solution
is
31
The
stiffness
matrix
is
precisely
the
Gram matrix appearing
in the
projection theorem;
see
page
62. If we
apply
the
projection theorem directly
to
compute
v
n
,
we
need
to
compute
the
right-hand-side vector
f
whose components
are
a(u,
</>i);
the
weak
form
allows
us to
compute
these
components
without
knowing
u,
since
a(it,(fo)
=
(/,
</>i).
32
That
is, in the
sense
that
it is
computationally expensive
to
compute
an
orthogonal basis.
Given
any
basis,
it is
simple
in
principle
to
apply
the
Gram-Schmidt procedure
to
obtain
an or-
thogonal basis.
The
reader
can
consult
any
introductory book
on
linear algebra
for an
explanation
of
the
Gram-Schmidt procedure.
5.5.
The
Galerkin method
183
This
is a system
of
n linear equations for
the
unknowns
Ul,
U2,
...
,
Un.
We define a
matrix
K E
Rnxn
and
a vector
fERn
by
(We now also have two meanings for
the
symbol "f":
the
function f
is
the
right-hand
side
of
the
differential equation, while
the
vector f has components Ii = (I,
<l>i).)
Finding
Vn
is now equivalent
to
solving
the
linear system
Ku=f.
The
matrix
K is usually called
the
stiffness matrix, since, when applied
to
problems
in mechanics,
the
entries in K
depend
on
the
stiffness k(x) of
the
material. For
analogous reasons,
the
vector f is usually called
the
load vector.31
The
reader will recall
that,
in computing a best approximation,
it
is
advan-
tageous
to
have
an
orthogonal basis, since
then
the
stiffness (or Gram)
matrix
is
diagonal,
and
the
projection is computed
by
n inner products. However,
the
basis
for
Vn
must be orthogonal with respect
to
the
energy inner
product,
and
with a
nonconstant coefficient k(x),
it
is usually difficult
32
to
find
an
orthogonal basis.
Therefore, in
the
finite element method,
we
will use a nonorthogonal basis.
We now illustrate
the
Galerkin
method
by applying
it
to
two BVPs, one with
constant
coefficients
and
the
other
with nonconstant coefficients.
Example
5.18.
Let
FN
be
the subspace
of
V spanned by the basis
{sin
(7fx)
, sin
(27fx)
,
...
,sin
(N
7fx)} ;
This basis is orthogonal with respect to the ordinary
L2
inner
product
on
the interval
[0,1].
Consider the
BVP
d
2
u
-
dx
2
=
X,
0 < x < 1,
u(O)
= 0,
u(l)
= 0
(this is (5.39) with k(x) = I}. The exact solution is
X x
3
u(x) = 6 -
6'
(5.47)
31The stiffness
matrix
is precisely
the
Gram
matrix
appearing
in
the
projection theorem; see
page 62.
If
we
apply
the
projection
theorem
directly
to
compute
Vn,
we
need
to
compute
the
right-hand-side vector f whose
components
are a(u, ¢i)j
the
weak form allows
us
to
compute
these
components
without
knowing u, since a(u,
¢i)
=
(j,
¢;).
3
2
That
is, in
the
sense
that
it
is
computationally
expensive
to
compute
an
orthogonal basis.
Given
any
basis,
it
is simple
in
principle
to
apply
the
Gram-Schmidt
procedure
to
obtain
an
or-
thogonal basis.
The
reader
can
consult any
introductory
book
on
linear algebra for
an
explanation
of
the
Gram-Schmidt
procedure.

and
Therefore,
and
the
basis
turns
out to be
orthogonal with
respect
to the
energy
inner product
as
well.
We
also
have
These
form
the
entries
of
the
matrix
K and the
vector
f.
Since
K is
diagonal,
we
can
solve
the
system
Ku = f
immediately
to
obtain
The
exact solution
is
We
will
apply
the
Galerkin method with
the
same approximating
subspace
and
basis
as
in the
previous exercise.
The
calculations
are
similar,
but the
bilinear form
changes
to
and
the
basis
functions
are no
longer orthogonal
in the
energy
inner product.
184
Chapter
5.
Boundary value problems
in
statics
Since
k(x)
=
I,
we see
that
The
resulting
approximation,
for N =
20,
is
displayed
in
Figure
5.10.
The
energy
inner product,
for a
constant function
k(x),
is
just
the L
2
inner product
applied
to
the
derivatives,
and so the
calculations
are
intimately related
to
those
we
perform
in
computing
a
Fourier series solution; indeed,
the final
result
is the
same!
Example
5.19.
Consider
the BVP
184
Chapter
5.
Boundary value problems
in
statics
Since
k(x)
= 1, we see
that
(1
du
dv
a(u,v)
=
10
dx(x)dx(x)dx
and
Therefore,
and
the basis
turns
out
to
be
orthogonal with respect
to
the energy
inner
product as
well.
We
also have
1
1 (_1)i+1
(x,
¢i)
= x sin (i1fx)
dx
=
-'----,..:-.
-
o ) Z1f
These
form
the entries
of
the
matrix
K
and
the vector
f.
Since K is diagonal, we
can solve the
system
K u = f
immediately
to obtain
2(-1)i+1
Ui
= ·3 3
2
1f
The resulting approximation, for N = 20, is displayed
in
Figure 5.10. The energy
inner
product, for a constant
function
k(x),
is
just
the £2
inner
product applied to
the derivatives, and so the calculations are
intimately
related to those we
perform
in
computing a Fourier series solution; indeed, the final result is the
same!
Example
5.19.
Consider the
BVP
The exact solution is
--
(l+x)-
=x,
d (
dU)
dx
dx
u(o) = 0,
u(l)
=
0.
° < x < 1,
( )
_
~
_ x
2
_
In
(1
+
x)
u x - 2 4
4In2'
(5.48)
We
will apply the Galerkin
method
with the
same
approximating subspace
and
basis
as
in
the previous exercise. The calculations are similar, but the bilinear
form
changes to
(1
du
dv
a(u,v)
=
10
(1
+
x)dx(x)dx(x)
dx,
and
the basis functions are no longer orthogonal
in
the energy
inner
product.
5.5.
The
Galerkin
method
185
We
have
These
form
the
entries
of
the
matrix
K and the
vector
f.
We
cannot solve
Ku
= f
explicitly;
that
is, we
cannot derive
a
useful
formula
for the
coefficients
Ui,i
=
1,2,...,
N,
in the
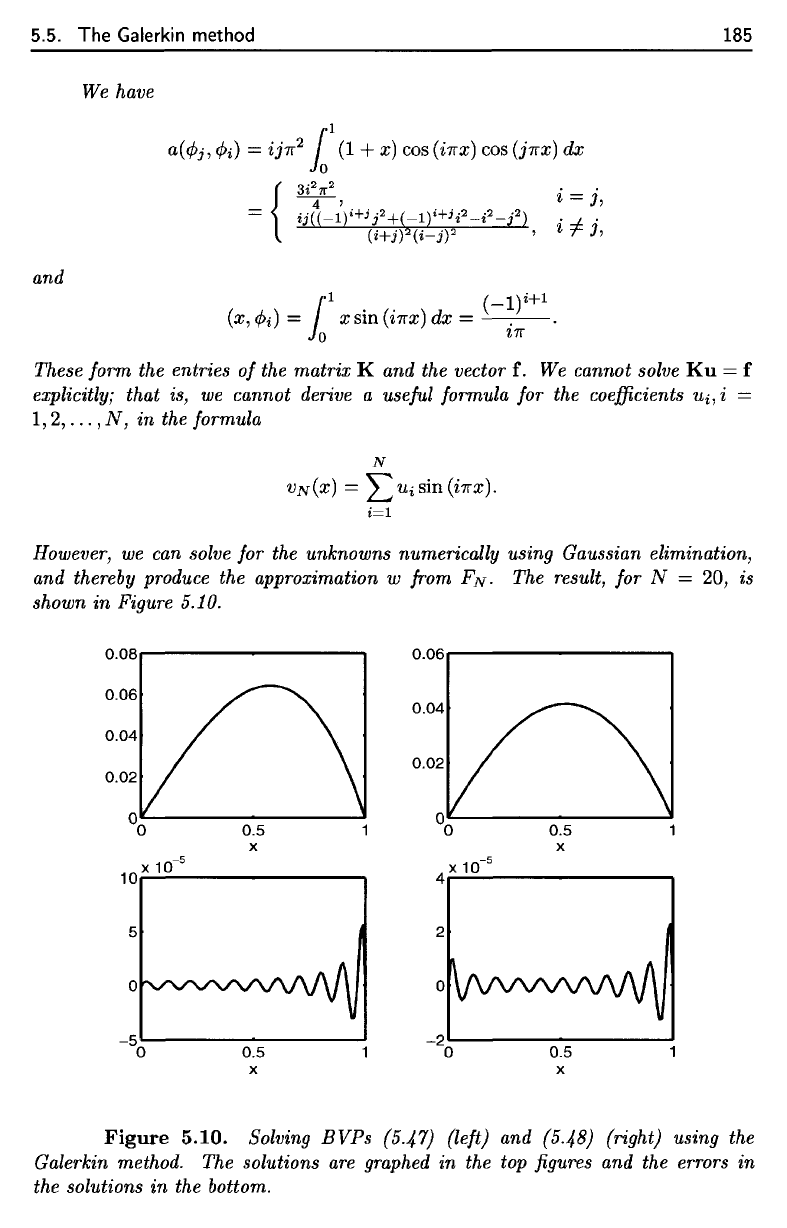
formula
However,
we can
solve
for the
unknowns numerically using Gaussian
elimination,
and
thereby produce
the
approximation
w
from
FN.
The
result,
for N =
20,
is
shown
in
Figure
5.10.
Figure
5.10. Solving BVPs (5.47)
(left)
and
(6.48)
(right) using
the
Galerkin method.
The
solutions
are
graphed
in the top
figures
and the
errors
in
the
solutions
in the
bottom.
and
5.5.
The
Galerkin
method
185
We have
a(¢>j,
¢>i)
= ij7r
2
11
(1
+ x) cos
(i7rx)
cos
(j7rX)
dx
={
and
1
1
(_I)i+l
(x,
¢>i)
= x sin
(i7rx)
dx =
-'---:-.
-
o
Z7r
These form the entries
of
the matrix K and the vector
f.
We cannot solve
Ku
= f
explicitly; that is,
we
cannot derive a useful formula for the coefficients
Ui,
i =
1,2,
...
,
N,
in
the formula
N
VN(X)
=
LUi
sin (i7rx).
i=1
However,
we
can solve for the unknowns numerically using Gaussian elimination,
and thereby produce the approximation w from F
N
.
The result, for N = 20, is
shown
in
Figure 5.10.
0.08.-----------.
-5
10
x
10
5
-5~---~----j
o
0.5
x
0.06.------------.
2
0.5
x
Figure
5.10. Solving
BVPs
{5.47}
{left} and
{5.48}
{right} using the
Galerkin method. The solutions
are
graphed
in
the top figures and the errors in
the solutions
in
the bottom.

186
Chapter
5.
Boundary value problems
in
statics
The
results
in
these
two
examples
are of
roughly
the
same quality, showing
that
the
Galerkin
method
can be as
effective
as the
Fourier method.
The
most
significant
difference
in
these
two
methods
is the
need
to
form
the
matrix
K in the
second
example
and
solve
the N x N
system
Ku =
f.
This
is
very time-consuming
compared
to the
computations required
in the first
example
(where
the
system
of
linear equations
is
diagonal).
This question
of
efficiency
is
particularly important
when
we
have
two or
three spatial dimensions;
in a
problem
of
realistic size,
it may
take impossibly long
to
solve
the
resulting linear system
if the
coefficient
matrix
is
dense.
A
dense matrix
is a
matrix
in
which
most
or all of the
entries
are
nonzero.
A
sparse
matrix,
on the
other hand,
has
mostly zero entries.
The finite
element method
is
simply
the
Galerkin method with
a
special choice
for
the
subspace
and its
basis;
the
basis
leads
to a
sparse
coefficient
matrix.
The
ultimate sparse,
nonsingular
matrix
is a
diagonal matrix. Obtaining
a
diagonal
matrix requires
that
the
basis
for the
approximating subspace
be
chosen
to be
orthogonal with respect
to the
energy inner product.
As
mentioned earlier,
it is too
difficult,
for a
problem with variable
coefficients,
to find an
orthogonal basis.
The
finite
element
method uses
a
basis
in
which most pairs
of
functions
are
orthogonal;
the
resulting matrix
is not
diagonal,
but it is
quite sparse.
Exercises
1.
Determine whether
the
bilinear
form
defines
an
inner product
on
each
of the
following
subspaces
of
(7
2
[0,^].
If it
does
not, show why.
2.
Show
that
if
FN
is the
subspace
defined
in
Example 5.18,
and the
Galerkin
method
is
applied
to the
weak
form
of
with
FJV
as the
approximating subspace,
the
result
will
always
be the
partial
Fourier sine series (with
N
terms)
of the
exact
solution
u.
3.
Define
5 to be the set of all
polynomials
of the
form
ax +
bx
2
,
considered
as
functions
defined
on the
interval
[0,1].
(a)
Explain
why 5 is a
subspace
of
C
2
[0,1].
186 Chapter
5.
Boundary value problems
in
statics
The
results in these two examples are of roughly the same quality, showing
that
the Galerkin method can be as effective as the Fourier method.
The
most
significant difference in these two methods
is
the need to form the matrix K in
the
second example and solve the N x N system
Ku
= f. This
is
very time-consuming
compared
to
the
computations required in the first example (where the system of
linear equations is diagonal). This question of efficiency
is
particularly important
when
we
have two or three spatial dimensions; in a problem of realistic size,
it
may
take impossibly long
to
solve the resulting linear system if the coefficient matrix
is
dense. A dense matrix
is
a matrix in which most or all of
the
entries are nonzero.
A sparse matrix, on the other hand, has mostly zero entries.
The finite element method
is
simply
the
Galerkin method with a special choice
for
the
subspace
and
its basis; the basis leads
to
a sparse coefficient matrix.
The
ultimate sparse, nonsingular matrix is a diagonal matrix. Obtaining a diagonal
matrix requires
that
the basis for the approximating subspace be chosen
to
be
orthogonal with respect to
the
energy inner product.
As
mentioned earlier,
it
is
too
difficult, for a problem with variable coefficients,
to
find an orthogonal basis.
The
finite element method uses a basis in which most pairs of functions are orthogonal;
the
resulting matrix is not diagonal,
but
it
is
quite sparse.
Exercises
1. Determine whether the bilinear form
defines
an
inner product on each of the following subspaces of C
2
[0,
fl.
If
it
does not, show
why.
(a)
{v
E C
2
[0,f] : v(f) =
O}
(b)
{v
E C
2
[0,f] :
v(O)
=
v(f)}
(c)
C
2
[0,f] (the entire space)
2.
Show
that
if FN
is
the subspace defined in Example 5.18, and the Galerkin
method
is
applied
to
the weak form of
d
2
u
-k
dx
2
=
f(x),
0 < x <
f,
u(O)
= 0,
u(f) = 0,
with FN as
the
approximating subspace,
the
result will always be the partial
Fourier sine series (with N terms) of
the
exact solution u.
3. Define S
to
be
the
set of all polynomials of the form
ax
+ bx
2
,
considered as
functions defined on the interval [0,1].
(a) Explain why
S
is
a subspace of C
2
[0,
1].

5.5.
The
Galerkin
method
187
(b)
Explain
why the
bilinear
form
defines
an
inner product
on
S.
(c)
Compute
the
best approximation
from
S,
in the
energy norm,
to
f(x]
=
e
x
.
(d)
Explain
why the
best approximation
from
P-2,
in the
energy norm,
to
f(x)
=
e
x
is not
unique. (The subspace
PI
is
defined
in
Exercise 3.1.3d.)
4.
Repeat Exercise
3
with
5.
Define
and
regard
¥2
as a
subspace
of
C|j[0,1].
Apply
the
Galerkin method, using
¥2
as the
approximating subspace,
to
estimate
the
solution
of
Find
the
exact solution
and
graph
the
exact
and
approximate solutions
to-
gether.
6.
Repeat Exercise
5
using
the
subspace
7.
The
standard Gaussian elimination algorithm
for
solving
Ax = b
requires
arithmetic operations when
A
e
R
nxn
.
(The exact number
is a
cubic poly-
nomial
in
n,
and
2n
3
/3
is the
leading term. When
n is
large,
the
lower
degree
terms
are
negligible
in
comparison
to the
leading term.)
(a)
Suppose
that,
on a
certain computer,
it
takes
1
second
to
solve
a 100 x 100
dense linear system
by
Gaussian elimination.
How
long
will
it
take
to
solve
a
1000
x
1000 system?
A
10000
x
10000 system?
5.5.
The Galerkin method
187
(b) Explain why
the
bilinear form
r
l
du dv
a(u,v)
=
10
dx
(x)
dx
(x) dx
defines
an
inner product on S.
(c) Compute the best approximation from
S,
in
the
energy norm,
to
f(x)
=
eX.
(d) Explain why
the
best approximation from
P2,
in
the
energy norm,
to
f(x) =
eX
is not unique. (The subspace
P2
is defined in Exercise 3.l.3d.)
4.
Repeat Exercise 3 with
s =
{v
E C
2
[0,
1]
v(x)
=
ax+
bx
2
+ cx
3
for some
a,b,c
E R}.
5.
Define
V
2
= span {
x(l
- x), x
(~
-
x)
(1
-
x)
}
and
regard V
2
as a subspace of C1[0,
1].
Apply
the
Galerkin method, using
V
2
as
the
approximating subspace,
to
estimate
the
solution of
d (
dU)
- dx
(1
+ x)
dx
=
x,
0 < x <
1,
u(O)
= 0,
u(l)
=
O.
Find
the
exact solution
and
graph
the
exact
and
approximate solutions to-
gether.
6.
Repeat Exercise 5 using
the
subspace
V3
= span
{X(l-
x),x
(~-
x)
(1-
x),x
(~-
x)
(~-
x)
(1-
x)}.
7.
The
standard
Gaussian elimination algorithm for solving
Ax
= b requires
arithmetic operations when A
E
Rnxn.
(The exact number is a cubic poly-
nomial in
n,
and
2n
3
/3 is
the
leading term. When n
is
large,
the
lower degree
terms are negligible in comparison
to
the leading term.)
(a) Suppose
that,
on a certain computer,
it
takes 1 second
to
solve a 100 x 100
dense linear system by Gaussian elimination. How long will
it
take
to
solve a 1000 x 1000 system? A 10000 x 10000 system?
