Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.

148
Chapter
5.
Boundary value problems
in
statics
to
indicate
this
fact.
As we saw in
Example
5.8,
this
does
not
necessarily imply
the
/N(X)
->•
f(x)
for all x
e
[0,^].
It
does imply, however,
that
/N
gets
arbitrarily
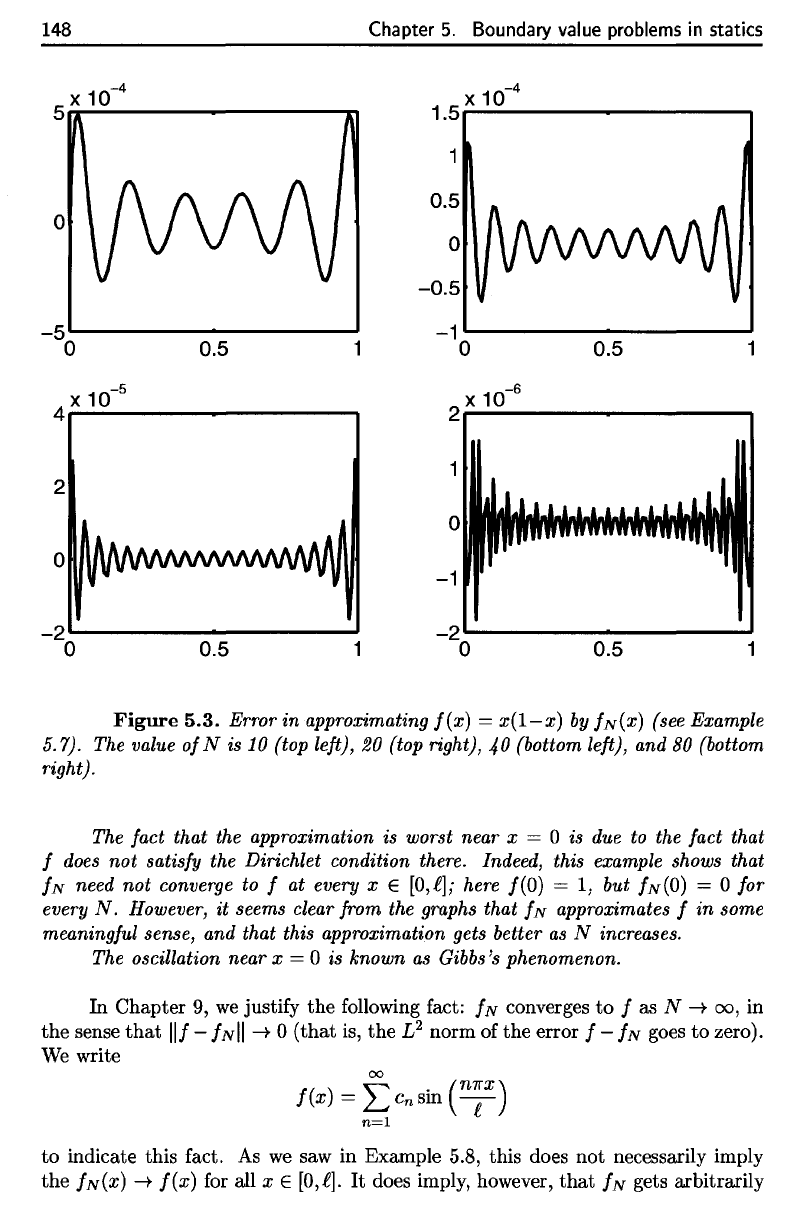
Figure
5.3. Error
in
approximating
f(x}
=
x(l—x)
by
/N(X)
(see Example
5.7).
The
value
of
N is 10
(top
left),
20
(top right),
40
(bottom
left),
and 80
(bottom
right).
The
fact that
the
approximation
is
worst near
x = 0 is due to the
fact that
f
does
not
satisfy
the
Dirichlet condition there. Indeed, this example shows that
/AT
need
not
converge
to f at
every
x
e
[0,€j;
here /(O)
= 1, but
/Ar(0)
= 0 for
every
N.
However,
it
seems clear from
the
graphs that
fw
approximates
f in
some
meaningful
sense,
and
that this approximation gets better
as N
increases.
The
oscillation near
x = 0 is
known
as
Gibbs's
phenomenon.
In
Chapter
9, we
justify
the
following fact:
/jv
converges
to / as N
—>
oo,
in
the
sense
that
||/
—
/AT||
—>
0
(that
is, the
L
2
norm
of the
error
/
—
/AT
goes
to
zero).
We
write
148
Chapter
5.
Boundary value problems
in
statics
1.5 x 10
-4
1
0.5
o
0
-0.5
-5~------------------~
-1
o 0.5
1
0 0.5
1
2
X1O
-6
1
2
-2~------------------~
-2~------------------~
o
0.5 1 o 0.5 1
Figure
5.3.
Error
in
approximating
f(x)
=
xCI-x)
by
fN(X) (see Example
5.7). The value
of
N is 10 (top left), 20 (top right),
40
(bottom left), and 80 (bottom
right).
The fact that the approximation
is worst near x = 0 is due to the fact that
f does
not
satisfy the Dirichlet condition there. Indeed, this example shows that
fN
need
not
converge to f at every x E
[0,£];
here f(O) =
1,
but fN(O) = 0 for
every
N.
However,
it
seems clear from the graphs
that
fN
approximates f
in
some
meaningful sense, and that this approximation gets better
as
N increases.
The oscillation near x = 0 is known
as
Gibbs's phenomenon.
In
Chapter
9,
we
justify
the
following fact:
fN
converges
to
f as N -+
00,
in
the
sense
that
Ilf - fNIl -+ 0
(that
is,
the
L2
norm of
the
error f -
fN
goes
to
zero).
We
write
00
f(x)
=
Lcnsin
(n;x)
n=l
to
indicate this fact.
As
we
saw in Example 5.8, this does
not
necessarily imply
the
fN(X) -+
f(x)
for all x E
[0,£].
It
does imply, however,
that
fN
gets arbitrarily
5.2.
Introduction
to the
spectral
method;
eigenfunctions
149
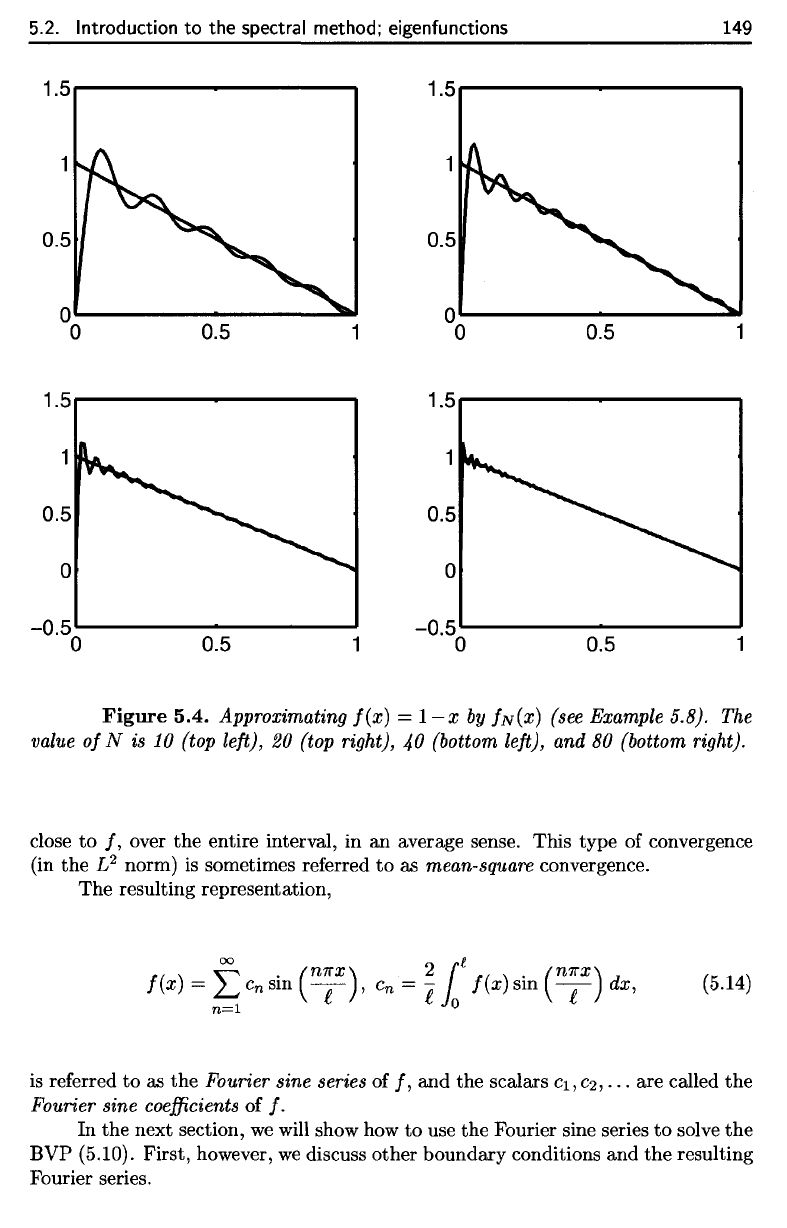
Figure
5.4. Approximating
/(#)
= 1
—
x by
/N(X)
(see Example 5.8).
The
value
of
N is 10
(top
left),
20
(top right),
40
(bottom
left),
and 80
(bottom
right).
close
to /,
over
the
entire interval,
in an
average sense. This type
of
convergence
(in
the
L
2
norm)
is
sometimes
referred
to as
mean-square convergence.
The
resulting representation,
is
referred
to as the
Fourier sine series
of /, and the
scalars
ci,C2,...
are
called
the
Fourier
sine
coefficients
of /.
In
the
next section,
we
will
show
how to use the
Fourier sine series
to
solve
the
BVP
(5.10).
First,
however,
we
discuss other boundary conditions
and the
resulting
Fourier series.
5.2. Introduction
to
the spectral method; eigenfunctions
149
1.5r----------...,
1.5r----------...,
1 1
0.5 0.5 1
1.5r----------..., 1.5r----------...,
1
1
-0.5'-------------'
o
0.5
1
-0.5'----------~
o 0.5 1
Figure
5.4. Approximating
f(x)
=
I-x
by
fN(X) (see Example 5.8). The
value
of
N is 10 (top left), 20 (top right),
40
(bottom left), and 80 (bottom right).
close
to
f,
over
the
entire interval, in
an
average sense. This
type
of convergence
(in
the
L2
norm) is sometimes referred
to
as mean-square convergence.
The
resulting representation,
= l
f(x)
= L C
n
sin
(n;x),
C
n
=
~
1
f(x)
sin
(n;x)
dx,
n=l
0
(5.14)
is referred
to
as
the
Fourier sine series
of
f,
and
the
scalars
Cl,
C2,
••.
are called
the
Fourier sine coefficients
of
f.
In
the
next section,
we
will show how
to
use
the
Fourier sine series
to
solve
the
BVP
(5.10). First, however,
we
discuss other
boundary
conditions
and
the
resulting
Fourier series.

The
operator
L
m
is
symmetric with positive eigenvalues,
it has a
trivial null space,
and the
range
of
L
m
is all of
C[0,^]
(see Exercise 5.1.6). Therefore,
L
m
u
= f has
a
unique solution
for
every
/
e
C[0,^],
and we
will
show,
in the
next section,
how
to
compute
the
solution
by the
spectral method.
First,
however,
we
must
find the
eigenvalues
and
eigenfunctions
of
L
m
.
Since
L
m
has
only positive eigenvalues,
we
define
A =
0
2
,
where
9 > 0, and
solve
150
Chapter
5.
Boundary value problems
in
statics
5.2.3
Eigenfunctions
under
other
boundary
conditions;
other
Fourier
series
We
now
consider
the BVP
with mixed boundary conditions,
which
models,
for
example,
a
hanging
bar
with
the
bottom
end
free.
In
order
to
consider
a
spectral method,
we
define
the
subspace
The
general solution
of the
differential
equation
is
The first
boundary condition,
u(Q)
= 0,
implies
that
c\
— 0, and
hence
any
nonzero
eigenfunction
must
be a
multiple
of
The
second boundary condition.
yields
the
condition
that
and the
operator
L
m
:
C^[0,€]
—>
C[0,l],
where
150
Chapter
5.
Boundary value problems
in
statics
5.2.3 Eigenfunctions under other boundary conditions; other
Fourier
series
We
now consider the BVP with mixed boundary conditions,
d'2u
-T
dx2
=f(x),
O<x<£,
u(O)
= 0, (5.15)
~~(£)=o,
which models, for example, a hanging
bar
with
the
bottom
end free. In order
to
consider a spectral method,
we
define the subspace
c![O,£]
=
{u
E C
2
[0,£]
:
u(O)
=
~~(£)
=
O}
and the operator Lm : C;,
[0,
£]
--+
C[O,
£],
where
d'2u
Lm
u
= -
dx
2
'
The
operator Lm
is
symmetric with positive eigenvalues, it has a trivial null space,
and
the range of Lm
is
all of
C[O,
£]
(see Exercise 5.1.6). Therefore, Lmu = f has
a unique solution for every f E
C[O,£],
and
we
will show, in
the
next section, how
to compute the solution by the spectral method. First, however,
we
must find the
eigenvalues and eigenfunctions of
Lm.
Since Lm has only positive eigenvalues,
we
define A =
(J2,
where B >
0,
and
solve
d'2u
2
dx
2
+ B u = 0, ° < x <
£,
u(O)
= 0,
(5.16)
du
dx
(£)
=
0.
The
general solution of the differential equation is
u(x) =
Cl
cos
(Bx)
+ C2 sin
(Bx).
The
first boundary condition,
u(O)
=
0,
implies
that
Cl
=
0,
and hence any nonzero
eigenfunction must be a multiple of
u(x) = sin
(Bx).
The
second boundary condition,
du
dx
(£)
= 0,
yields the condition
that
B cos
(B£)
=
0.

5.2. Introduction
to the
spectral
method;
eigenfunctions
151
Since
0 > 0 by
assumption, this
is
possible only
if
Since
The
resulting representation,
is
referred
to as the
Fourier quarter-wave sine series.
It is
valid
in the
mean-square
sense.
Example
5.9.
Let
f(x)
= x
and
i =
1.
Then
or
Solving
for A, we
obtain
eigenvalues
AI,
A2,...,
with
The
corresponding eigenfunctions
are
The
eigenfunctions
are
orthogonal,
as is
guaranteed since
L
m
is
symmetric,
and as can be
verified
directly
by
computing
(0
n
,^>
TO
).
The
best approximation
to
/
G
C[0,£],
using
0i,02,...,0jv,
is
(5.17) becomes
where
5.2. Introduction
to
the
spectral method; eigenfunctions
Since 0 > 0 by assumption, this is possible only
if
or
cos
(OC)
= 0
OC
=
~,
37r
2
2'···'
(2n -
1)7r
2
Solving for
A,
we
obtain
eigenvalues
A1,
A2'
...
' with
,
....
(2n -
1)27r
2
An
=
4C2
' n =
1,2,3,
....
The
corresponding eigenfunctions are
.
((2n
- l)7rX)
cPn(x)=sm
2C
'
n=1,2,3,
....
151
The
eigenfunctions are orthogonal, as
is
guaranteed since
Lm
is
symmetric,
and as can
be
verified directly by computing
(cPn,
cPm).
The
best approximation
to
f E
e[O,
C],
using
cP1,
cP2,
.
..
,
cPN,
is
(5.17)
Since
r£.2((2n-1)7rX)
£
(cPn,
cPn)
=
10
sm
2C
dx =
2'
(5.17) becomes
N
f(
)
==
'"'
b .
((2n
- l)7rX)
x
~
n
sm
2C
'
n=l
where
b
n
=
~
1£
f(x)
sin
((2n
;c
1
)7rx) dx, n
=
1,2,3,
....
The
resulting representation,
f(
)
-~b
.
((2n-1)7rX)
x -
~
n
sm
2£
'
n=l
is referred
to
as
the
Fourier quarter-wave sine series.
It
is valid in
the
mean-square
sense.
Example
5.9.
Let
f(x)
= x and £ = 1. Then
21
1 .
((2n-1)7rx)d
_ 8(-1)n+1
xsm
x-
(2
1)22'
n=1,2,3,
...
,
o 2
n-
7r
152
Chapter
5.
Boundary
value
problems
in
statics
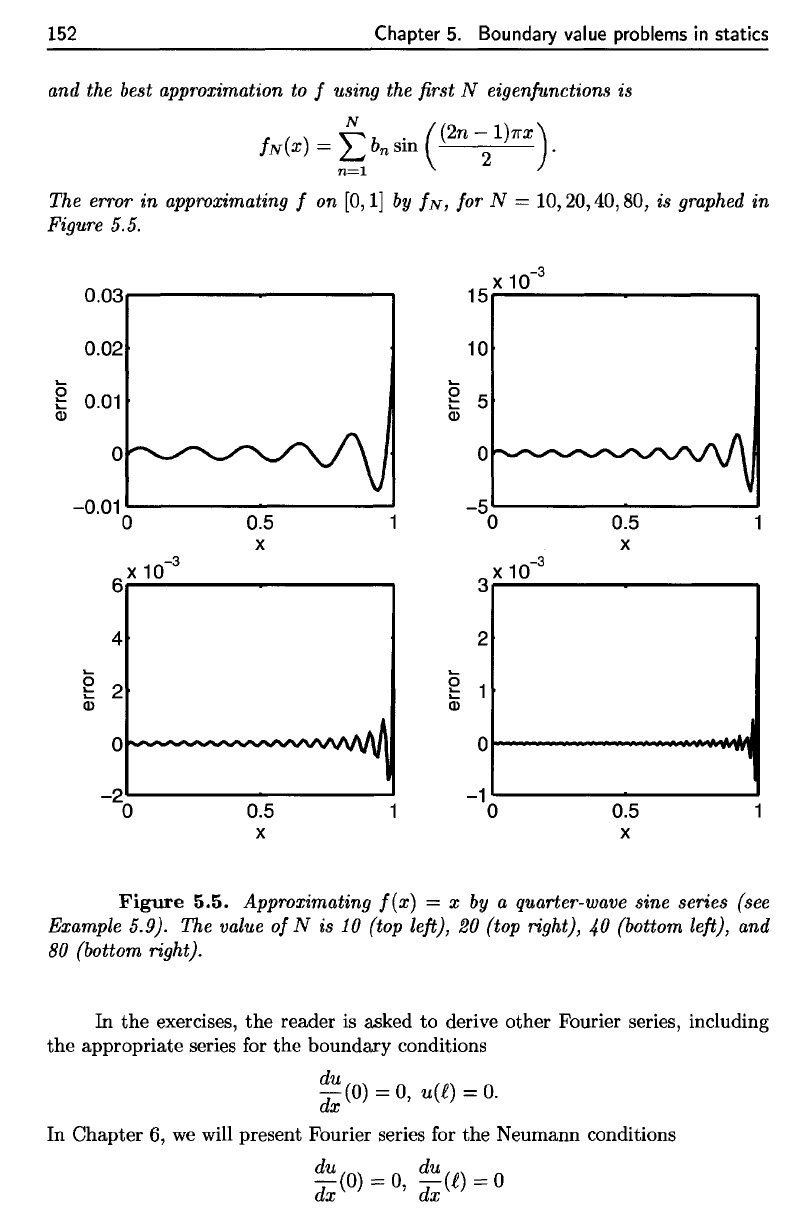
The
error
in
approximating
f on
[0,1]
by
/N,
for N =
10,20,40,80,
is
graphed
in
Figure
5.5.
Figure
5.5. Approximating
f(x)
— x by a
quarter-wave sine series (see
Example
5.9).
The
value
of
N is 10
(top
left),
20
(top right),
40
(bottom
left),
and
80
(bottom right).
In
the
exercises,
the
reader
is
asked
to
derive other Fourier series, including
the
appropriate
series
for the
boundary conditions
and
the
best
approximation
to f
using
the first N
eigenfunctions
is
In
Chapter
6, we
will
present Fourier series
for the
Neumann conditions
152
Chapter
5.
Boundary value problems
in
statics
and
the best approximation to f using the first N eigenfunctions is
N
f
(
)
-
""'
b .
((2n
-1)7fX)
N x -
~
n
sm
2 .
n=l
The error
in
approximating f on [0,1] by
fN,
for N = 10,20,40,80, is graphed
in
Figure 5.5.
0.03,....----------,
0.02
....
g
0.01
Q)
-0.01
'---------~
o
4
....
g 2
Q)
a
0.5
X
-2~------------------~
a
0.5
x
....
0
....
....
Q)
....
0
....
....
Q)
15
X 10-
3
10
5
0
-5
0
3
X1O
-3
2
1
0
-1
a
0.5
x
0.5
x
.&.
...
,
Figure
5.5.
Approximating
f(x)
= x by a quarter-wave sine series (see
Example 5.9). The value
of
N is 10 (top left), 20 (top right),
40
(bottom left),
and
80 (bottom right).
In
the
exercises,
the
reader
is asked
to
derive
other
Fourier series, including
the
appropriate
series for
the
boundary
conditions
du
dx
(0)
= 0, u(£) =
0.
In
Chapter
6, we will present Fourier series for
the
Neumann
conditions
du
(0)
=
0,
du
(£)
= °
dx dx

5.2.
Introduction
to the
spectral
method;
eigenfunctions
153
and the
periodic boundary conditions
(for
the
interval
[—i,f\).
Generally speaking, given
a
symmetric
differential
opera-
tor,
a
sequence
of
orthogonal eigenfunctions exists,
and it can be
used
to
represent
functions
in a
Fourier series. However,
it may not be
easy
to find the
eigenfunctions
in
some cases (see Exercise
4).
Exercises
1.
Use the
trigonometric identity
to
verify
that,
if n
/
m,
then
(V>n?
V'm)
— 0,
where
^1,^25^3?
• • •
are
given
in
(5.13).
2.
Define
K as in
Exercise
5.1.8.
We
know
(from
the
earlier exercise)
that
K has
only
real, positive eigenvalues. Find
all of the
eigenvalues
and
eigenvectors
of
K
3-.
Repeat Exercise
2 for the
differential
operator
Lfh
defined
in
Exercise
5.1.7.
The
resulting eigenfunctions
are the
quarter-wave
cosine functions.
4.
(Hard)
Define
LR
as in
Exercise
5.1.11.
(a)
Show
that
LR
has
only positive eigenvalues.
(b)
Show
that
LR
has an
infinite
sequence
of
positive eigenvalues. Note:
The
equation
that
determines
the
positive eigenvalues cannot
be
solved
analytically,
but a
simple graphical analysis
can be
used
to
show
that
they exist
and to
estimate their values.
(c)
For
o:
= K = 1, find the first two
eigenpairs
by finding
accurate
estimates
of
the two
smallest eigenvalues.
5.
(Hard)
Consider
the
differential
operator
M
:
C^[0,1]
->•
C[0,1]
defined
by
(recall
that
C£[0,1]
=
{u
e
C
2
[0,1]
:
u(0)
=
g(l)
=
0}).
Analyze
the
eigen-
pairs
of M as
follows:
(a)
Write down
the
characteristic polynomial
of the ODE
Using
the
quadratic formula,
find the
characteristic roots.
5.2. Introduction
to
the
spectral method; eigenfunctions 153
and
the
periodic boundary conditions
du du
u(
-P)
= u(P), dx
(-P)
= dx
(P)
(for
the
interval [-P,
P]).
Generally speaking, given a symmetric differential opera-
tor, a sequence of orthogonal eigenfunctions exists,
and
it
can
be
used
to
represent
functions in a Fourier series. However,
it
may
not
be easy
to
find
the
eigenfunctions
in some cases (see Exercise 4).
Exercises
1.
Use
the
trigonometric identity
1
sin a sin,8 = 2 (cos
(a
-
,8)
- cos
(a
+
,8))
to
verify
that,
if n
¥-
m,
then
('¢n,
'¢m)
=
0,
where
'¢l,
'1/J2,
'¢3,
...
are given in
(5.13).
2.
Define K as in Exercise 5.1.8.
We
know (from
the
earlier exercise)
that
K has
only real, positive eigenvalues. Find all of
the
eigenvalues and eigenvectors of
K.
3·.
Repeat Exercise 2 for
the
differential operator
Lin
defined in Exercise 5.1.7.
The
resulting eigenfunctions are
the
quarter-wave cosine functions.
4.
(Hard)
Define
LR
as in Exercise 5.1.11.
(a) Show
that
LR
has only positive eigenvalues.
(b) Show
that
LR
has
an
infinite sequence of positive eigenvalues. Note:
The
equation
that
determines
the
positive eigenvalues cannot be solved
analytically,
but
a simple graphical analysis can be used
to
show
that
they exist
and
to
estimate their values.
(c) For a
=
1£
=
1,
find
the
first two eigenpairs by finding accurate estimates
of
the
two smallest eigenvalues.
5.
(Hard)
Consider
the
differential operator M :
C~[O,
1]
-+
C[O,
1]
defined by
cFu
du
Mu=--+~+5u
dx
2
dx
(recall
that
C~[O,
1]
=
{u
E C
2
[0,
1]
:
u(O)
=
~~(1)
=
o}).
Analyzetheeigen-
pairs of M as follows:
(a) Write down
the
characteristic polynomial of
the
ODE
d
2
u du
dx
2
-
dx
+
(A
- 5)u =
O.
(5.18)
Using
the
quadratic formula, find
the
characteristic roots.

154
Chapter
5.
Boundary value problems
in
statics
(b)
There
are
three cases
to
consider, depending
on
whether
the
discriminant
in
the
quadratic formula
is
negative, zero,
or
positive
(that
is,
depending
on
whether
the
characteristic
roots
are
complex conjugate,
or
real
and
repeated,
or
real
and
distinct).
In
each case, write down
the
general
solution
of
(5.18).
(c)
Show
that
in the
case
of
real roots (either repeated
or
distinct),
there
is
no
nonzero
solution.
(d)
Show
that
there
is an
infinite sequence
of
values
of A,
leading
to
complex
conjugate
roots,
each yielding
a
nonzero solution
of
(5.18).
Note:
The
equation
that
determines
the
eigenvalues cannot
be
solved analytically.
However,
a
simple graphical analysis
is
sufficient
to
show
the
existence
of
the
sequence
of
eigenvalues.
(e)
Find
the first two
eigenpairs
(that
is,
those
corresponding
to the two
smallest eigenvalues), using some numerical method
to
compute
the first
two
eigenvalues accurately.
(f)
Show
that
the first two
eigenfunctions
are not
orthogonal.
6.
Define
Find necessary
and
sufficient
conditions
on the
coefficients
an,012,021?
#22
for
the
operator
L^
to be
symmetric.
7.
Compute
the
Fourier sine series,
on the
interval
[0,1],
for
each
of the
following
functions:
29
29
The use of
Mathematica
or
some other program
to
compute
the
necessary integrals
is
recom-
mended.
Graph
the
error
in
approximating each function
by 10
terms
of the
Fourier
sine series.
154 Chapter
5.
Boundary
value
problems
in
statics
(b) There are three cases to consider, depending on whether the discriminant
in the quadratic formula
is
negative, zero, or positive
(that
is, depending
on whether the characteristic roots are complex conjugate, or real and
repeated, or real and distinct). In each case, write down the general
solution of (5.18).
(c) Show
that
in
the
case
of real roots (either repeated or distinct), there
is
no nonzero solution.
(d) Show
that
there
is
an infinite sequence of values of
A,
leading
to
complex
conjugate roots, each yielding a nonzero solution of (5.18). Note: The
equation
that
determines
the
eigenvalues cannot be solved analytically.
However, a simple graphical analysis is sufficient to show the existence
of the sequence of eigenvalues.
(e)
Find
the
first two eigenpairs
(that
is, those corresponding
to
the
two
smallest eigenvalues), using some numerical method
to
compute the first
two eigenvalues accurately.
(f) Show
that
the first two eigenfunctions are not orthogonal.
6.
Define
and define
Lb
:
GUO,
£]
-+
G[O,
f] by
Find necessary and sufficient conditions on the coefficients
au,
a12, a21,
a22
for
the operator
Lb
to
be symmetric.
7.
Compute the Fourier sine series, on the interval
[0,
1],
for each of the following
functions:
29
(a)
g(x) = x
(b)
hex)
=!
-Ix-!I
(c)
m(x)=x-x
3
(d)
k(x) = 7x - 10x
3
+ 3x
5
Graph the error in approximating each function by
10
terms of
the
Fourier
sine series.
29The use
of
Mathematica
or
some
other
program
to
compute
the
necessary integrals is recom-
mended.

5.3.
Solving
the BVP
using Fourier
series
155
8.
Explain
why a
Fourier sine series,
if it
converges
to a
function
on [0,
£],
defines
an odd
function
of x € R. (A
function
/ : R
->•
R is
odd
if
f(—x)
=
—f(x)
for
all x
e
R.)
9.
What
is the
Fourier sine series
of
/(#)
= sin
(3-rrx)
on the
interval
[0,1]?
10.
Repeat Exercise
7
using
the
quarter-wave
sine series (see Section
5.2.S).
29
11.
Repeat
Exercise
7
using
the
quarter-wave
cosine series (see
Exercise
3).
29
5.3
Solving
the BVP
using Fourier
series
We
now
return
to the
problem
of
solving
the BVP
which
can be
expressed simply
as LDU =
f.
5.3.1
A
special case
We
begin with
a
special case
that
is
easy
to
solve. Suppose
/ is of the
form
where
the
coefficients
ci,
C2,...,
CN
are
known.
We
then look
for the
solution
in the
form
By
construction,
u G
C|j[0,£],
and so
u
satisfies
the
boundary conditions (regardless
of the
values
of
bi,
62,
• •
•,
&w)-
We
therefore choose
the
coefficients
&i,
62,...,
&AT
so
that
the
differential
equation
is
satisfied.
Since
u is
expressed
in
terms
of the
eigenfunctions,
the
expression
for LDU is
very
simple:
The
equation
LDU = f
then becomes
5.3. Solving
the
BVP using Fourier series 155
8. Explain why a Fourier sine series,
if
it
converges
to
a function
on
[0,
e],
defines
an
odd
function of x E
R.
(A function f : R
-+
R is
odd
if
f(
-x)
= -
f(x)
for all x E R.)
9.
What
is
the
Fourier sine series of
f(x)
= sin
(37fx)
on
the
interval
[0,
I]?
10. Repeat Exercise 7 using
the
quarter-wave sine series (see Section 5.2.3).29
11.
Repeat
Exercise 7 using
the
quarter-wave cosine series (see Exercise
3).29
5.3
Solving
the
BVP
using
Fourier
series
We
now
return
to
the
problem of solving
the
BVP
cPu
-T
dx
2
=
f(x),
° < x <
e,
u(o) = 0,
(5.19)
u(e)
= 0,
which can
be
expressed simply as
LDU
= f.
5.3.1 A special case
We
begin with a special case
that
is easy
to
solve. Suppose f is
of
the
form
N
f(x) = L C
n
sin
(n;x),
n=l
(5.20)
where
the
coefficients
Cl,
C2,
•••
,
CN
are known.
We
then
look for
the
solution in
the
form
N
u(x) = L b
n
sin
(n;x).
n=l
By construction, U E C1[0,
e],
and
so U satisfies
the
boundary
conditions (regardless
of
the
values of b
l
,
b
2
,
..•
, b N
).
We
therefore choose
the
coefficients b
l
,
b
2
,
.••
, b N so
that
the
differential equation
is
satisfied.
Since u is expressed in terms of
the
eigenfunctions,
the
expression for
LDu
is
very simple:
The
equation
LDu
= f
then
becomes
N 2 N
""
Tn
7f2
.
(n7fx)
""
. (n7fx)
~~bnsm
-e- =
~cnsm
-e- .
n=l
n=l
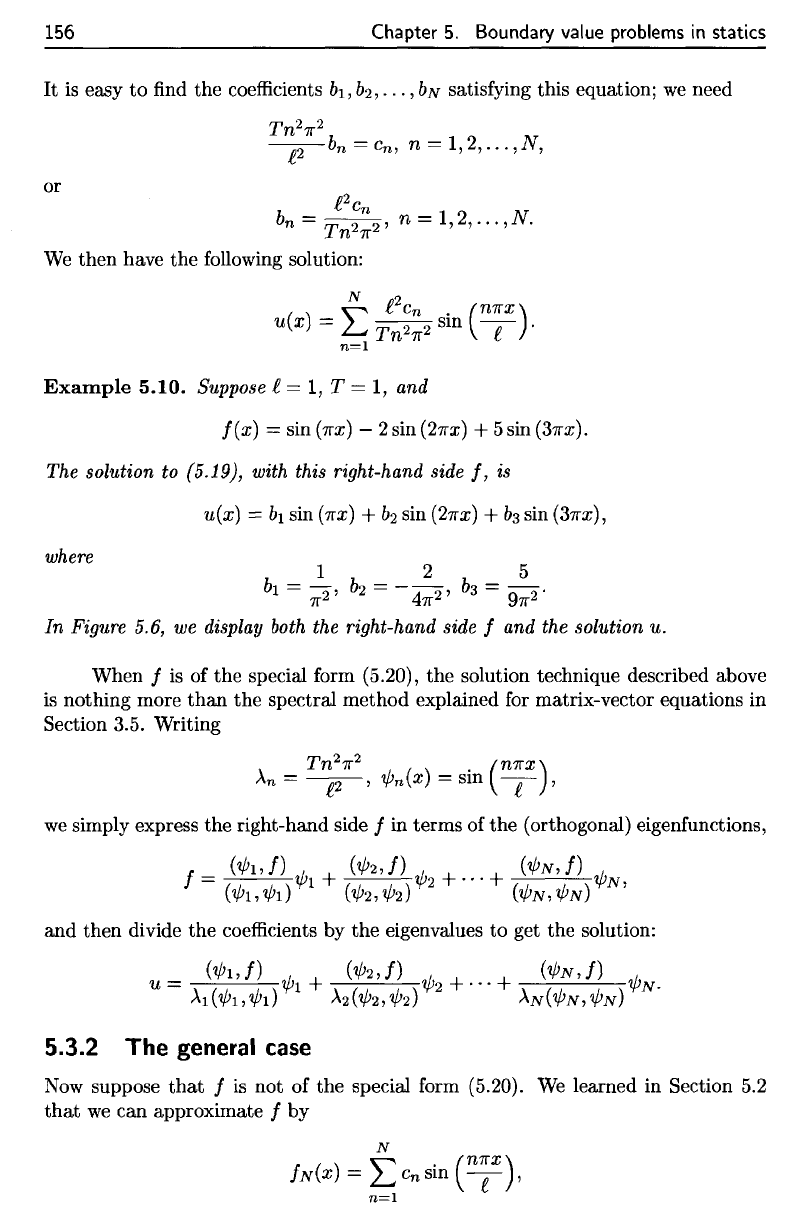
156
Chapter
5.
Boundary
value
problems
in
statics
It is
easy
to find the
coefficients
&i,
62,
• • •
?
&AT
satisfying
this equation;
we
need
or
We
then have
the
following
solution:
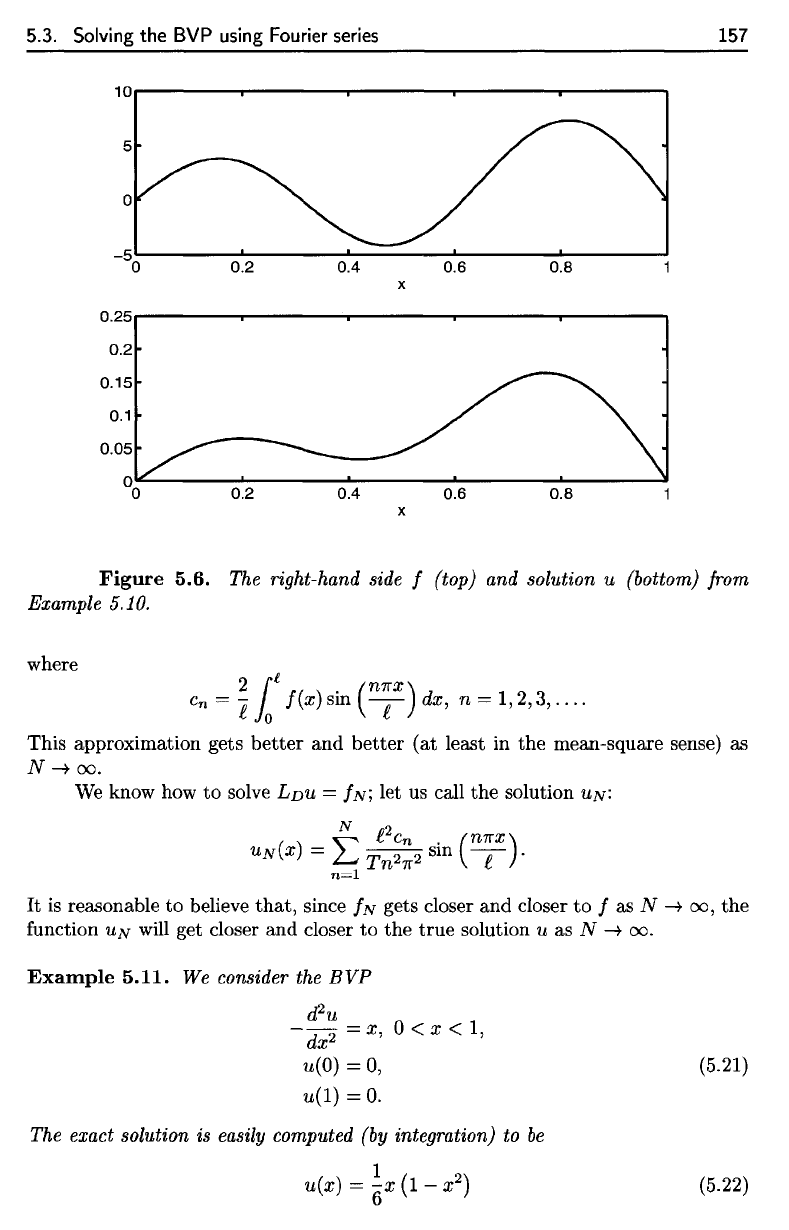
Example
5.10.
Suppose
t
—
I,
T =
I,
and
The
solution
to
(5.19),
with this right-hand
side
f,
is
where
In
Figure
5.6,
we
display
both
the
right-hand
side
f and the
solution
u.
When
/ is of the
special
form
(5.20),
the
solution technique described above
is
nothing more
than
the
spectral method explained
for
matrix-vector
equations
in
Section
3.5. Writing
we
simply express
the
right-hand side
/ in
terms
of the
(orthogonal) eigenfunctions,
and
then divide
the
coefficients
by the
eigenvalues
to get the
solution:
5.3.2
The
general
case
Now
suppose
that
/ is not of the
special
form
(5.20).
We
learned
in
Section
5.2
that
we can
approximate
/ by
156
Chapter
5.
Boundary value problems
in
statics
It
is easy
to
find the coefficients b
1
,
b
2
,
...
,
bN
satisfying this equation;
we
need
Tn
2
7r
2
~bn
= c
n
, n = 1,2,
...
,N,
or
C
2
C
n
b
n
=
-T
2
2'
n = 1,2,
...
,N.
n7r
We
then
have
the
following solution:
N
02
()
'"'
<-
C
n
.
(n7rX)
u x
=
~
Tn
2
7r
2
8m
-C-
.
n=l
Example
5.10.
Suppose C = 1, T = 1, and
I(x)
= sin
(7rx)
- 2 sin
(27rx)
+ 5 sin (37rx).
The solution to
(5.19), with this right-hand side
I,
is
where
u(x)
==
b
1
sin
(7rx)
+ b
2
sin
(27rx)
+ b
3
sin (37rx),
125
b
1
=
7r2'
b
2
= - 47r2'
b3
=
97r
2
'
In
Figure 5.6,
we
display
both
the right-hand side I and the solution u.
When
I is of
the
special form (5.20),
the
solution technique described above
is nothing more
than
the
spectral
method
explained for matrix-vector equations in
Section 3.5. Writing
Tn
2
7r
2
(n7rx)
An
=~,
'¢n(X)
= sin
-C-
,
we
simply express
the
right-hand side I in
terms
of
the
(orthogonal) eigenfunctions,
and
then
divide
the
coefficients by
the
eigenvalues
to
get the solution:
5.3.2 The general case
Now suppose
that
I is
not
of
the
special form (5.20). We learned in Section 5.2
that
we
can approximate I by
5.3.
Solving
the BVP
using Fourier
series
157
Figure
5.6.
The
right-hand side
f
(top)
and
solution
u
(bottom) from
Example
5.10.
where
This
approximation gets
better
and
better
(at
least
in the
mean-square sense)
as
TV
-»•
oo.
We
know
how to
solve
Lpu
—
/AT;
let us
call
the
solution
UN-
It is
reasonable
to
believe
that,
since
/N
gets
closer
and
closer
to / as N
—>
oo,
the
function
UN
will
get
closer
and
closer
to the
true solution
u as N
—>
oo.
Example
5.11.
We
consider
the BVP
The
exact solution
is
easily
computed
(by
integration)
to be
5.3. Solving
the
BVP using Fourier series 157
10r--------T--------~------~--------~------_,
x
0.25
0.2
0.15
0.1
0.05
0.2 0.4 0.6
O.B
x
Figure
5.6.
The right-hand side f (top) and solution u (bottom) from
Example 5.10.
where
C
n
=
~
1£
f(x)
sin
(n;x)
dx, n =
1,2,3,
....
This approximation gets
better
and
better
(at
least in the mean-square sense) as
N
--+
00.
We
know how
to
solve
LDu
= fN; let us call
the
solution
UN:
~
f
2
C
n
.
(n'JTx)
UN(X) =
~
Tn
2
'JT2
sm
-g-
.
n=l
It
is
reasonable
to
believe
that,
since
fN
gets closer
and
closer
to
f as N
--+
00,
the
function
UN
will get closer and closer
to
the
true
solution U as N
--+
00.
Example
5.11.
We consider the
BVP
d
2
u
- dx
2
=
X,
0 < x <
1,
u(O)
= 0,
u(l)
=
O.
The exact solution is easily computed (by integration) to
be
1
u(x) =
6x
(1
- x
2
)
(5.21)
(5.22)
