Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


where
k =
In
(2)/2.
Here
m(t)
is the
mass
of the
isotope
at
time
t
(seconds),
and the
differential
equation indicates
that
a
constant
fraction
of the
atoms
are
disintegrating
at
each point
in
time.
The
above
differential
equation holds,
of
course,
when none
of the
isotope
is
being added
or
taken away
by
other means.
Suppose
that
initially
10
g of the
isotope
are
present,
and
mass
is
added
from
an
external source
at the
constant
rate
of 0.1
g/s. Solve
the
IVP
modeling this
situation, using
the
Green's
function,
and
determine
the
long-time behavior
of
m(t).
4.
Find
the
Green's
function
for the IVP
128
Chapter
4.
Essential ordinary differential equations
what
will
the
population
be at the
beginning
of
2000
(t =
10)?
Use the
Green's
function
to find
P(t)
and
then
P(10).
3. A
certain radioactive isotope decays exponentially according
to the law
5.
Use the
Green's
function
from
the
previous exercise
to
solve
6.
Use the
property
and a
change
of
variables
to
justify
(4.45),
4.7
Suggestions
for
further reading
There
are
many introductory textbooks
on
ODEs, such
as the
text
by
Goldberg
and
Potter
[18].
An
introductory
text
with
a
particularly strong emphasis
on
applied
mathematics
is
Boyce
and
DiPrima
[5].
A
more advanced book
that
focuses
on
the
theory
of
ODEs (and
the
necessary linear algebra)
is
Hirsch
and
Smale
[26].
The
reader
is
referred
to
Hirsch
and
Smale
for a
complete description
of the
theory
of
linear, constant-coefficient systems.
(We
covered only
a
special case,
albeit
an
important one,
in
Section 4.3.)
128
Chapter
4.
Essential ordinary differential equations
what will the population be
at
the beginning of
2000
(t = 10)? Use the
Green's function to find
P(t)
and then P(10).
3.
A certain radioactive isotope decays exponentially according
to
the law
dm
-=-km
dt '
where k =
In
(2)/2. Here
m(t)
is
the
mass of the isotope
at
time t (seconds),
and
the differential equation indicates
that
a constant fraction of the atoms are
disintegrating
at
each point in time. The above differential equation holds, of
course, when none of the isotope
is
being added or taken away by other means.
Suppose
that
initially 10 g of
the
isotope are present, and mass is added from
an
external source
at
the constant
rate
of
0.1
g/s. Solve the IVP modeling this
situation, using the Green's function, and determine the long-time behavior
of
m(t).
4.
Find the Green's function for the IVP
rf2u
dt
2
+
4u
=
f(t),
u(O)
= 0,
~~(O)
=
O.
5.
Use
the
Green's function from the previous exercise to solve
d
2
u
dt
2
+
4u
=
cos
(t),
u(O)
= 0,
~~
(0)
=
O.
6.
Use the property
o E
[a,
b]:::}
lab
8(t)g(t) dt =
g(O)
and
a change of variables
to
justify (4.45).
4.7 Suggestions for further reading
There are many introductory textbooks on ODEs, such as the text by Goldberg and
Potter
[18].
An introductory
text
with a particularly strong emphasis on applied
mathematics
is
Boyce
and
DiPrima
[5].
A more advanced book
that
focuses on
the
theory of ODEs (and the necessary linear algebra)
is
Hirsch and Smale
[26].
The reader
is
referred to Hirsch
and
Smale for a complete description of the theory
of linear, constant-coefficient systems. (We covered only a special case, albeit an
important one, in Section 4.3.)

4.7. Suggestions
for
further
reading
129
For
more information
on
numerical methods
for
ODEs,
the
reader
is
referred
to
Shampine
[43]
or
Lambert
[33].
Most books
on
numerical analysis, such
as
Atkinson
[2]
and
Kincaid
and
Cheney [30], also cover numerical methods
for
ODEs,
as
well
as the
background material
on
quadrature
and
interpolation.
The
text
by
Mattheij
and
Molenaar [38] gives
an
integrated presentation
of the
theory
and
numerical analysis
of
ODEs,
as
well
as
their
use for
modeling physical
systems.
4.7. Suggestions for further reading
129
For more information on numerical methods for ODEs, the reader is referred
to
Shampine
[43]
or Lambert
[33].
Most books on numerical analysis, such as Atkinson
[2]
and
Kincaid and Cheney
[30],
also cover numerical methods for ODEs, as
well
as
the
background material on quadrature and interpolation.
The
text
by Mattheij and Molenaar
[38]
gives
an
integrated presentation of the
theory and numerical analysis of ODEs, as well as their use for modeling physical
systems.
This page intentionally left blank
This page intentionally left blank

Our
first
examples
of
partial
differential
equations (PDEs)
will
arise
in the
study
of
static
(equilibrium) phenomena
in
mechanics
and
heat
flow. To
make
our
introduc-
tion
to the
subject
as
simple
as
possible,
we
begin with one-dimensional examples;
that
is, all of the
variation
is
assumed
to
occur
in one
spatial
direction. Since
the
phenomena
are
static,
time
is not
involved,
and the
single
spatial
variable
is the
only
independent variable. Therefore,
the
"PDEs"
are
actually ODEs! Nevertheless,
the
techniques
we
develop
for the
one-dimensional problems generalize
to
real PDEs.
Chapter
5
5.1 The
analogy between BVPs
and
linear algebraic
systems
As
mentioned
in
Chapter
3, the
solution methods presented
in
this book bear strong
resemblance,
at
least
in
spirit,
to
methods
useful
for
solving
a
linear system
of the
form
Ax = b. In the
exercises
and
examples
of
Chapter
3, we
showed some
of
the
similarities between linear systems
and
linear BVPs.
We now
review
these
similarities,
and
explain
the
analogy
further.
We
will
use the
equilibrium displacement
u
of a
sagging string
as our first
example.
In
Section 2.3,
we
showed
that
u
satisfies
the BVP
where
T is the
tension
in the
string
and / is an
external
force
density
(in
units
of
force
per
length).
If
A
e
R
mxn
,
then
A
defines
an
operator mapping
R
n
into
R
m
,
and
given
b
e
R
m
,
we can ask the
following
questions:
Is
there
an x
e
R
n
which
is
mapped
to b by A?
131
Boundary
In statice
Chapter 5
dary value problems
Our
first examples
of
partial
differential equations
(PDEs)
will arise in
the
study
of
static
(equilibrium)
phenomena
in mechanics
and
heat
flow. To make
our
introduc-
tion
to
the
subject
as simple as possible, we begin
with
one-dimensional examples;
that
is, all
of
the
variation
is
assumed
to
occur in one
spatial
direction. Since
the
phenomena
are
static,
time
is
not
involved,
and
the
single
spatial
variable is
the
only
independent variable. Therefore,
the
"PDEs"
are
actually ODEs! Nevertheless,
the
techniques we develop for
the
one-dimensional problems generalize
to
real
PDEs.
5.1 The analogy between BVPs and linear algebraic
systems
As mentioned in
Chapter
3,
the
solution methods presented
in
this
book
bear
strong
resemblance,
at
least in spirit,
to
methods
useful for solving a linear system of
the
form
Ax
=
b.
In
the
exercises
and
examples of
Chapter
3, we showed some of
the
similarities between linear systems
and
linear
BVPs.
We now review these
similarities,
and
explain
the
analogy further.
We will use
the
equilibrium displacement. u of a sagging
string
as
our
first
example.
In
Section 2.3, we showed
that
u satisfies
the
BVP
d2u
-T
dx
2
=
f(x),
0 < x <
£,
u(O)
= 0,
(5.1)
u(£)
= 0,
where T is
the
tension in
the
string
and
f
is
an
external
force density (in units of
force
per
length).
If
A E RIDxn,
then
A defines
an
operator
mapping
Rn
into
RID,
and
given
bE
RID,
we
can
ask
the
following questions:
• Is
there
an
x
ERn
which is
mapped
to
b by
A?
131

132
Chapter
5.
Boundary value problems
in
statics
If
so, is x
unique?
How
can
such
an x be
computed?
In
much
the
same way,
defines
an
operator—usually
referred
to as a
differential
operator.
For
convenience,
we
will
refer
to
this operator
as L. It
maps
one
function
to
another,
and the
differential
ermation
can
be
interpreted
as the
following question: Given
a
function
/
defined
on the
interval
[0,^],
does there exist
a
function
u
which
is
mapped
to / by L?
That
is,
does there exist
a
function
u
satisfying
Lu = /?
The
analogy between
Ax
=
b and Lu = f is
strengthened
by the
fact
that
the
differential
operator
L is
linear, just
as is the
operator
defined
by the
matrix
A.
Indeed,
if u and v are two
functions
and a and
{3
are
scalars, then
Underlying
this
calculation
is the
fact
that
a
space
of
functions
can be
viewed
as
a
vector
space—with
functions
as the
vectors.
The
operator
L is
naturally
defined
on
the
space
(7
2
[0,£|
introduced
in
Section 3.1. Thus
L
takes
as
input
a
twice-
continuously
differentiable
function
u and
produces
as
output
a
continuous
function
Tjii..
Example
5.1. Consider
the
function
u
:
[0,1]
—>
R
defined
by
The
function
u is
continuous
on
[0,1]
(we
need
only
check
that
the two
cubic
pieces
have
the
same
value
at x —
1/2, which they do).
We
have
and
it is
easy
to see
that
both
quadratic
pieces
defining
du/dx
have value
1/8 at
x —
1/2.
Therefore,
du/dx
is
continuous
on
[0,1].
Finally,
132
Chapter
5.
Boundary value problems
in
statics
•
If
so, is x unique?
• How can such
an
x
be
computed?
In
much
the
same way,
d
2
-T-
dx
2
defines
an
operator-usually
referred
to
as a differential operator. For convenience,
we
will refer
to
this
operator
as
L.
It
maps one function
to
another,
and
the
differential equation
d
2
u
- T dx
2
= f (x), ° < x < £
(5.2)
can
be
interpreted as
the
following question: Given a function f defined
on
the
interval [0,£], does there exist a function u which is mapped
to
f by L?
That
is,
does
there
exist a function u satisfying
Lu
=
f?
The
analogy between
Ax
= b
and
Lu
= f is strengthened by
the
fact
that
the
differential
operator
L is linear,
just
as
is
the
operator
defined by
the
matrix
A.
Indeed, if u
and
v are two functions
and
a
and
(3
are
scalars,
then
~
L(au
+
(3v)
=
-T
dx
2
[au +
(3v]
~u
~v
=-aT--(3T-
dx
2
dx
2
=
aLu
+
(3Lv.
Underlying
this
calculation is
the
fact
that
a space of functions can be viewed as
a vector
space-with
functions as
the
vectors.
The
operator
L is
naturally
defined
on
the
space C
2
[0,£]
introduced in Section 3.1.
Thus
L takes as
input
a twice-
continuously differentiable function u
and
produces as
output
a continuous function
Lu.
Example
5.1.
Consider the function u : [0,1]
---+
R defined
by
° < x <
~,
~<x<1.
The function u is continuous on [0,1]
(we
need only check that the two cubic pieces
have the same value at x
= 1/2, which they do). We have
du {
~
(x - x
2
) ,
dx(x)=
~(x2_X+~),
° < x <
~,
~
< x < 1,
and
it
is easy to
see
that both quadratic pieces defining
du/dx
have value
1/8
at
x = 1/2. Therefore,
du/dx
is continuous on
[0,1].
Finally,
~u
{
dx
2
(x) =
l-x
2 '
1
x-
2'
° < x <
~,
~
< x < 1,
5.1.
The
analogy
between
BVPs
and
linear
algebraic
systems
133
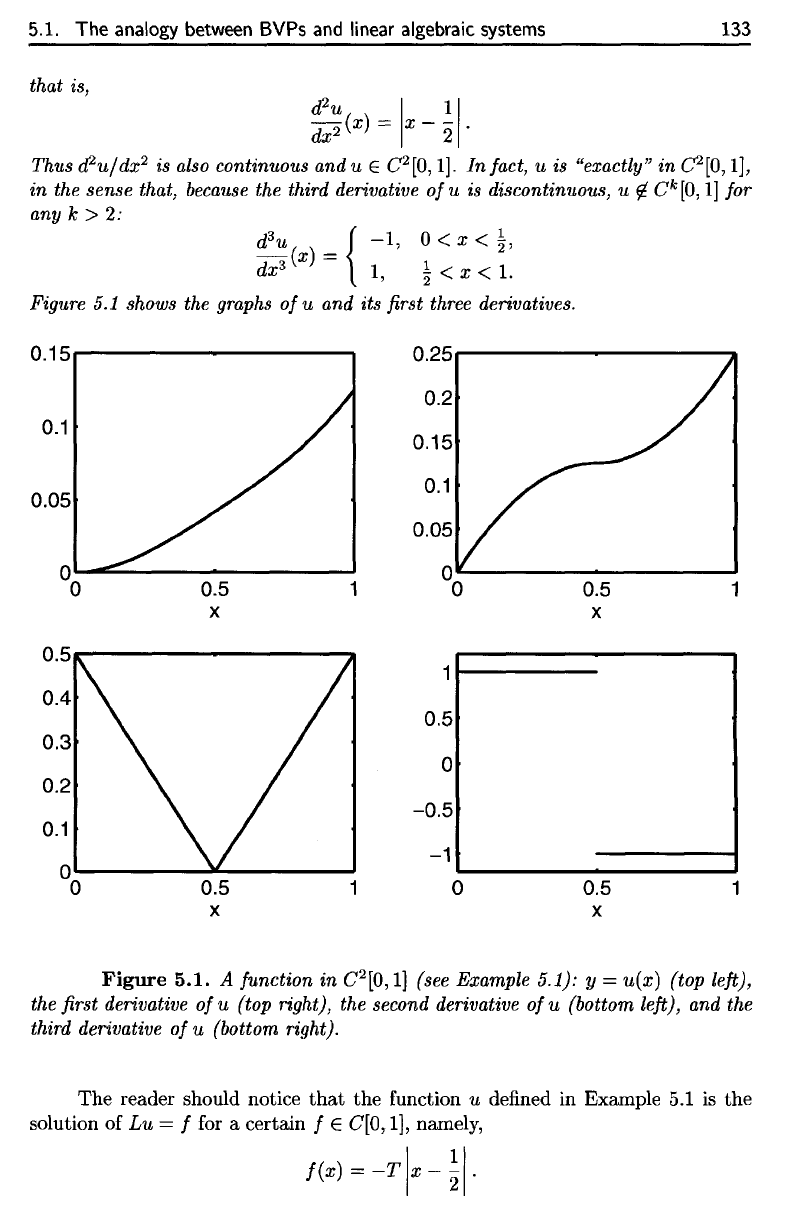
Figure
5.1
shows
the
graphs
of
u and its first
three
derivatives.
Figure
5.1.
A
function
in
(7
2
[0,1]
(see Example 5.1):
y
=
u(x)
(top
left),
the first
derivative
of
u
(top right),
the
second derivative
of
u
(bottom
left),
and the
third derivative
of
u
(bottom right).
The
reader
should
notice
that
the
function
u
defined
in
Example
5.1
is the
solution
of Lu = f for a
certain
/ 6
C[0,1],
namely,
that
is,
Thus
d?u/dx
2
is
also
continuous
andu
E
C
2
[0,1].
In
fact,
u is
"exactly"
in
C
2
[0,1],
in the
sense
that,
because
the
third derivative
of
u is
discontinuous,
u
$.
C
k
[Q,
1] for
any
k > 2:
5.1. The analogy between BVPs
and
linear algebraic systems
133
that
is,
::~(x)
=
Ix
-
~I·
Thus
cPu/dx
2
is also continuous
and
u E C
2
[0,
1].
Infact,
u is "exactly"
in
C
2
[0,
1],
in
the sense that, because the third derivative
of
u is discontinuous, u
f/.
Ck
[0,
1]
for
any
k > 2:
d
3
u X _
{-I,
0< x <
~,
dx
3
( ) -
1,
~
< x <
1.
Figure 5.1 shows the graphs
of
u
and
its first three derivatives.
0.15
0.1
0.05
0.1
0
0
0.5 1
X
0.5
0
-0.5
0.1
-1
0.5
1 0
X
0.5 1
X
0.5 1
X
Figure
5.1.
A
function
in
C
2
[0,
1]
(see Example 5.1): y =
u(x)
(top left),
the first derivative
of
u (top right), the second derivative
of
u (bottom left),
and
the
third derivative
of
u (bottom right).
The reader should notice
that
the function u defined in Example
5.1
is
the
solution of
Lu
= f for a certain f E
C[O,
1],
namely,
f(x)
=
-Tlx
-
~I·

and
/
must
be
equal
at
each
x
e
[0,£J.
Here, though,
we see a
major
difference:
Lu
= f
represents
an
infinite
number
of
equations, since there
is an
infinite
number
of
points
x
e
[0,£j.
Also,
there
are
infinitely
many unknowns, namely,
the
values
u(x),xe
[0,4
The
role
of the
boundary conditions
is not
difficult
to
explain
in
this context.
Just
as a
matrix
A 6
R
mxn
can
have
a
nontrivial null space,
in
which case
Ax =
b
cannot have
a
unique solution,
so a
differential
operator
can
have
a
nontrivial
null
space.
It is
easy
to
verify
that
the
null space
of L
consists
of all first-degree
polynomial
functions:
Therefore,
Lu = /
cannot have
a
unique solution, since
if
u
is one
solution
and
w(x]
= ax + b,
then
u +
w
is
another solution.
On the
other hand,
Lu = f
does
have solutions
for
every
/
e
C^O,^];
for
example,
solves
Lu =
f.
This
is
equivalent
to
saying
that
the
range
of L is all of
C[0,4
Example
5.2.
Let f
G
C[0,1]
be
defined
by
f(x)
— x.
Then,
for
every
a, b
e
R,
is a
solution
of Lu =
f.
That
is, the
general
solution
of Lu — f
consists
of
u(x)
=
—x
3
/(6T)
plus
any
function from
the
null
space
of
L.
(See
page
43.)
The
fact
that
the
null space
of L is
two-dimensional suggests
that
the
operator
equation
Lu = f is
closely analogous
to a
linear algebraic equation
Ax = b,
where
A is an (n
—
2) x n
matrix
and
H(A)
=
R
n
~
2
(that
is, the
columns
of A
span
R
n
~
2
).
In the
same way,
Lu
—
j
represents
a
collection
of
equations, namely,
the
conditions
that,
the
functions
It is
possible
to
take
the
analogy
of Lu = f
with
Ax = b
even further.
If
A
G
R
mxn
,
then
Ax
=
b
represents
m
equations
in n
unknowns, each equation
having
the
form
On
the
other hand,
if we
define
v =
du/dx,
then
v is not the
solution
of Lu = f
for
any / £
C[0,1]
(because
d?v/dx
2
is
discontinuous).
Indeed,
Lv is not
defined,
strictly speaking, since dv/dx
is not
differentiable
on the
entire interval
[0,1].
Thus
it
makes sense
to
regard
the
domain
of L as
(7
2
[0,1]:
134
Chapter
5.
Boundary
value
problems
in
statics
134
Chapter
5.
Boundary value problems
in
statics
On
the
other hand, if
we
define v =
du/dx,
then
v is not
the
solution of
Lu
= J
for any J E
C[O,
1]
(because
rPv/dx
2
is
discontinuous). Indeed,
Lv
is
not defined,
strictly speaking, since
dv/dx
is
not
differentiable on
the
entire interval [0,1]. Thus
it
makes sense
to
regard
the
domain of
Las
C
2
[0,
1]:
L:
C
2
[0,
1]-t
C[O,
1].
It
is possible
to
take
the
analogy of
Lu
= f with
Ax
= b even further.
If
A E Rffixn,
then
Ax
= b represents m equations in n unknowns, each equation
having
the
form
In
the
same way,
Lu
= J represents a collection of equations, namely,
the
conditions
that
the
functions
_T
rPu
dx
2
and
J must be equal
at
each x E
[0,
fl.
Here, though,
we
see a
major
difference:
Lu
= f represents
an
infinite number of equations, since there is
an
infinite number
of points
x E
[0,
fl.
Also, there are infinitely many unknowns, namely,
the
values
u(x),
x E
[O,f].
The
role of
the
boundary conditions
is
not
difficult
to
explain in this context.
Just
as a
matrix
A E Rffixn can have a nontrivial null space, in which case
Ax
==
b cannot have a unique solution, so a differential operator can have a nontrivial
null space.
It
is easy
to
verify
that
the
null space of L consists of all first-degree
polynomial functions:
N(L)=={u:
u(x)=ax+b,
a,bER}.
Therefore,
Lu
= J cannot have a unique solution, since if u
is
one solution
and
w(x)
==
ax
+
b,
then
u + w
is
another solution.
On
the
other
hand,
Lu
= f does
have solutions for every
f E C[O,f]; for example,
1rr
u(x)
=
-Iji
10 10
J(z)dzds
solves
Lu
= f. This is equivalent
to
saying
that
the
range of L is all of
C[O,£].
Example
5.2.
Let
f E
C[O,
1]
be
defined
by
f(x)
==
x.
Then, for every a,
bE
R,
1
u(x)
==
-
6Tx3
+
ax
+ b
is a solution
of
Lu
=
f.
That is, the general solution
of
Lu
==
f consists
of
u(x)
=
-x
3
/(6T)
plus any function from the null space
of
L.
(See page 43.)
The
fact
that
the
null space of L is two-dimensional suggests
that
the
operator
equation
Lu
==
f is closely analogous
to
a linear algebraic equation
Ax
==
b,
where
A is
an
(n-2)
x n
matrix
and
R(A)
==
Rn-2
(that
is, the columns of A span
Rn-2).

5.1.
The
analogy between BVPs
and
linear algebraic systems
135
Such
a
matrix
A has the
property
that
Ax = b has a
solution
for
every
b €
R
n
2
,
but the
solution
cannot
be
unique.
Indeed,
in
this
case,
M(A)
is
two-dimensional,
and
therefore
so is the
solution
set of Ax = b for
every
b
e
R
n
.
In
order
to
obtain
a
unique solution,
we
must
restrict
the
allowable vectors
x by
adding
two
equations.
Example
5.3.
Let A
e
R
2x4
be
defined
by
Then
it is
easy
to
show that
N
(A)
=
span{vi,v<2},
where
(It
is
also
easy
to see
that
"^-(A)
=
R
2
;
since
the first two
columns
of
A are
linearly
independent.) Thus,
«/x
e
R
4
satisfies
Ax =
0,
then there exist
s,t € R
such that
In
order
to
narrow down
a
unique
solution,
we
must
impose additional conditions
that
force
s and t to
both
be
zero.
If we are to
preserve
the
linear nature
of the
problem, these conditions will simply
be two
more linear equations,
of the
form
where
w,z
are two
vectors
in
R
4
.
There
are
many vectors
w and z
that will work;
indeed,
as
long
as
w
;
z, and the two
rows
of A
form
a
linearly independent
set,
then
these additional equations will result
in a
unique solution.
For
example,
let w
=
ei
=
(1,0,0,0)
and z =
64
=
(0,0,0,1).
Then (5.3)
and
(5-4)
together imply
and
the
only
solution
to
this system
is s = t = 0.
Therefore,
the
only
vector
x
G
R
satisfying
(5.3)
and
(5.4)
is x = 0.
The
matrix
A
e
R
2x4
defines
an
operator mapping
(Kx.
—
Ax).
One way to
understand
the
role
of the
additional equations
ei
• x = 0
and
64
-x
= 0 is
that they allow
us to
define
a
matrix
B
e
R
4x4
and a
vector
c 6
R
4
5.1. The analogy between BVPs and linear algebraic systems
135
Such a
matrix
A has
the
property
that
Ax
= b has a solution for every b E
Rn-2,
but
the
solution
cannot
be
unique. Indeed,
in
this
case,
N(A)
is two-dimensional,
and
therefore so is
the
solution set of
Ax
= b for every b
ERn.
In
order
to
obtain
a unique solution,
we
must
restrict
the
allowable vectors x by adding two equations.
Example
5.3.
Let
A E R
2x4
be
defined
by
_
[-1
2
-1
° ]
A - °
-1
2
-1
.
Then
it
is easy to show that
N(A)
=
span{vl'
V2},
where
(It is also easy to see that
R(A)
=
R2,
since the first two columns
of
A are linearly
independent.) Thus,
if
x E
R4
satisfies
Ax
=
0,
then there exist s, t E R such that
x =
SVl
+
tV2.
(5.3)
In
order to narrow down a unique solution,
we
must
impose additional conditions
that force
sand
t to both
be
zero.
If
we
are
to preserve the linear nature
of
the
problem, these conditions will simply
be
two more linear equations,
of
the form
w·x=o,
z·x
= 0,
(5.4)
where
W,
z are two vectors in R
4
•
There are
many
vectors
wand
z that will work;
indeed,
as
long
as
w,
z, and the two rows
of
A form a linearly independent set,
then these additional equations will result in a unique solution.
For example, let w =
el
=
(1,0,0,0)
and z = e4 =
(0,0,0,1).
Then (5.3) and
(5.4) together imply
s = 0,
s +
3t
= 0,
and the only solution to this system is s
= t =
0.
Therefore, the only vector x E R4
satisfying
(5.3) and (5.4) is x =
o.
The
matrix
A E R
2
x4
defines an operator mapping
(Kx
=
Ax).
One way to understand the role
of
the additional equations
el
. x = °
and e4·X = 0 is that they allow us to define a
matrix
BE
R
4X4
and a vector c E R4

136
Chapter
5.
Boundary value problems
in
statics
such that
By
=
c has a
unique solution
related
in a
simple
way to a
solution
of
Ax
=
b. The
matrix
B
would
be
However,
this
way
of
looking
at the
situation
does
not
generalize
in a
natural
way to
differential
equations.
Therefore,
we
interpret
the two
side equations
as
restricting
the
domain
of the
operator.
The
equations
are
satisfied
by
vectors
of the
form
(and
only
by
vectors
of
this form), where
62
=
(0,1,0,0)
and
63
=
(0,0,1,0).
Therefore,
by
imposing
the
equations
(5.5),
we are
allowing
only
solutions
to Ax =
b
that
belong
to the
subspace
We
define
a new
operator
KS : S
—>
R
2
by
restriction:
KS*.
= Kx (so KS is
the
same
as
K,
except
that
we
restrict
the set of
allowable
inputs).
We
have
then
shown that
the
operator
KS has a
trivial null
space—the
only
solution
to KSX = 0 is
x = 0. By the
same token,
for any b €
R
2
,
there
is a
unique solution
to
KS~X.
= b.
The
final
step
in
this example
is to
interpret
the
operator equation
K§x
= b
as
a
matrix-vector equation. After all,
KS is a
linear operator
defined
on finite-
dimensional vector spaces,
and it
therefore
must
be
representable
by a
matrix.
We
write vectors
x
e
5 in
terms
of
their coordinates with
respect
to the
basis
{62,
e
3
}:
We
can
thus
identify
S
with
R
2
:
The
matrix
revresentinq
K$
is
therefore
2x2,
and the
reader
can
show
26
that this
matrix
is
26
The
reader should recall
from
Exercise 3.1.8
that
there
is a
canonical method
for
computing
the
matrix representing
a
linear operator
on finite-dimensional
spaces:
The
columns
of the
matrix
are
the
images under
the
operator
of the
standard basis vectors.
If u =
(1,0),
then
K$u
= (2,
—1),
and so the first
column
of C
must
be
The
second column
of C is
determined
by
computing
the
image
of
(0,1)
under
KS-
136
Chapter
5.
Boundary value problems
in
statics
such that
By
= c has a unique solution related
in
a simple way to a solution
of
Ax
=
b.
The matrix B would
be
B=
l
-~
°
°
° °
2
-1
-1
2
° °
However, this way
of
looking at the situation does
not
generalize
in
a natural way to
differential equations. Therefore,
we
interpret the two side equations
as
restricting
the domain
of
the operator.
The equations
are satisfied by vectors
of
the form
el
. x = 0,
e4·
x = °
(5.5)
(and only
by
vectors
of
this form), where
e2
= (0,1,0,0) and
e3
= (0,0,1,0).
Therefore, by imposing the equations (5.5), we
are
allowing only solutions to
Ax
=
b that belong to the subspace
S = span{e2,e3}.
We define a new operator
Ks
: S
-t
R2 by restriction:
Ksx
=
Kx
(so
Ks
is
the same
as
K,
except that
we
restrict the set
of
allowable inputs). We have then
shown that the operator
Ks
has a trivial null
space-the
only solution to
Ksx
= 0 is
x =
o.
By
the same token, for any
bE
R2, there is a unique solution to
Ksx
=
b.
The final step
in
this example is to interpret the operator equation
Ksx
= b
as
a matrix-vector equation.
After
all,
Ks
is a linear operator defined on finite-
dimensional vector spaces, and
it
therefore
must
be
representable
by
a matrix. We
write vectors
xES
in
terms
of
their coordinates with respect to the basis {e2, e3}:
xES:::}
x = Ule2 +
U2e3.
We can thus identify S with R2:
x =
Ul
e2
+
U2e3
E S B u E R
2
.
The
matrix
representing
Ks
is therefore 2 x
2,
and the reader can
show2
6
that this
matrix
is
[
2
-1]
c =
-1
2 .
26The
reader
should recall from Exercise 3.1.8
that
there
is a canonical
method
for
computing
the
matrix
representing a linear
operator
on finite-dimensional spaces:
The
columns
of
the
matrix
are
the
images
under
the
operator
of
the
standard
basis vectors.
If
u = (1,0),
then
Ksu
=
(2,
-1),
and
so
the
first column
of
C
must
be
[
-i
] .
The
second column
of
C is
determined
by
computing
the
image
of
(0,1)
under
Ks.

5.1.
The
analogy between BVPs
and
linear algebraic systems
137
By
inspection,
we can see
that
C is
nonsingular,
as
expected,
and,
as an
added
bonus,
C is a
symmetric matrix, whereas
the
matrix
B
;
obtained from
the
other
point
of
view
described
above,
is not
symmetric.
We
now
show
that
the
role
of the
boundary
conditions
in
(5.1)
is
exactly
analogous
to the
role
of the
extra equations
ei
• x
=
0,
62
• x = 0 in the
above
example.
We
view
the
boundary conditions
as
restricting
the
domain
of the
operator
I/,
and
define
where
by
This
new
operator
LD has a
trivial null space. Indeed,
if u
e
C
2
[0,l]
satisfies
then
u(x)
= ax + b for
some
a, b
e
R. If u
also satisfies
w(0)
=
u(t]
= 0,
then
a
= b = 0, and u is the
zero function.
The
operator
LD,
like
L,
has the
property
that
LDU
= f has a
solution
for
each
/ €
(7[0,1]
(that
is, the
range
of LD is
C[0,
£]),
and
this solution
is
unique because
the
null space
of LD is
trivial.
We
next
show
that
LD is a
symmetric
operator,
and,
as
such,
it has
many
of
the
properties
of a
symmetric matrix.
Before
we can
demonstrate this,
of
course,
we
must explain what symmetry means
for a
differential
operator.
In
Section 3.5,
we
saw
that
a
matrix
A €
R
nxn
is
symmetric
if and
only
if
We
can
make
the
analogous definition
for a
differential
operator, using
the
L
2
inner
product
in
place
of the dot
product.
Definition
5.4.
Let S be a
subspace
of
C
k
[a,
b], and let K
:
S
—>•
C[a,
b]
be a
linear
operator.
We say
that
K is
symmetric
if
where
(-,-)
represents
the
L
2
inner product
on the
interval
[a,b].
That
is, K is
symmetric
if,
whenever
u,v
€ S, and
w
= Ku, z = Kv,
then
5.1.
The
analogy between BVPs and linear algebraic systems
137
By
inspection,
we
can see
that
C is nonsingular,
as
expected, and, as an added
bonus,
C is a
symmetric
matrix,
whereas the
matrix
B,
obtained from the other
point
of
view described above, is
not
symmetric.
We
now show
that
the
role of
the
boundary
conditions in (5.1)
is
exactly
analogous
to
the
role
of
the
extra
equations
el
. x = 0,
e2
. x = ° in
the
above
example.
We
view
the
boundary
conditions
u(o)
= u(£) = °
as restricting
the
domain of
the
operator
L,
and
define
where
by
LD
:
C1[0,£]-+
C[O,£],
c1[0,£]
=
{u
E C
2
[0,£]
: u(O) = u(£) =
O},
d
2
u
LDu
=
Lu
=
-T
dx
2
'
This new
operator
LD has a trivial null space. Indeed, if u E C
2
[0,
£]
satisfies
~u
-T
dx2
=0,
then
u(x)
=
ax
+ b for some a, b E
R.
If
u also satisfies u(O) = u(£) = 0,
then
a = b = 0,
and
u is
the
zero function.
The
operator L
D
,
like
L,
has
the
property
that
LDu
= f has a solution for each f E
C[O,
£]
(that
is,
the
range
of
LD
is
C[O,
£]),
and
this solution
is
unique because
the
null space
of
LD
is trivial.
We
next
show
that
LD
is a
symmetric
operator, and, as such,
it
has many of
the
properties
of
a symmetric matrix. Before
we
can demonstrate this,
of
course,
we must explain
what
symmetry means for a differential operator. In Section 3.5,
we
saw
that
a
matrix
A E
Rnxn
is symmetric if
and
only if
(Ax)·
y =
X·
(Ay) for all
x,y
ERn.
We
can make
the
analogous definition for a differential operator, using
the
L2 inner
product
in place
of
the
dot product.
Definition
5.4.
Let
5
be
a subspace
of
Ck[a,
bj,
and let K : 5
-+
C[a,
bj
be
a linear
operator.
We
say
that
K is symmetric
if
(Ku,
v) =
(u,Kv)
for
all
u,v
E 5, (5.6)
where
(.,.)
represents the L2
inner
product
on
the interval
[a,
b].
That is, K is
symmetric
if, whenever
u,v
E 5, and w =
Ku,
Z =
Kv,
then
lb
w(x)v(x)
dx
=
lb
u(x)z(x)
dx.
