Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


108
Chapter
4.
Essential
ordinary
differential
equations
10
steps
of RK4 use 40
evaluations
of
f(t,u).
In
problems
of
realistic
complexity,
the
evaluation
of
f(t,u]
is the
most expensive
part
of the
calculation
(often
/ is
defined
by a
computer
simulation
rather
than
a
simple
algebraic
formula),
and so
a
more
reasonable
comparison
of
these
results would conclude
that
RK4 is 4
times
as
efficient
as
Euler's
method
for
this
particular
example
and
level
of
error.
Higher-
order
methods
tend
to use
enough fewer
steps
than
lower-order methods
that
they
are
more
efficient
even though
they
require more work
per
step.
4.4.3
Numerical
methods
for
systems
of
ODEs
The
numerical
methods
presented
above
can be
applied
directly
to a
system
of
ordinary differential
equations.
Indeed,
when
the
system
is
written
in
vector form,
the
notation
is
virtually
identical.
We now
present
an
example.
Example
4.10. Consider
two
species
of
animals
that
share
a
habitat,
and
suppose
one
species
is
prey
to the
other.
Let
x\
(t) be the
population
of
the
predator species
at
time
t,
and let
X2(t)
be the
population
of the
prey
at the
same
time.
The
Lotka-
Volterra
predator-prey model
for
these
two
populations
is
where
ei,
62,
#,
r are
positive constants.
The
parameters have
the
following interpre-
tations:
BI
describes
the
attack rate
of the
predators (the rate
at
which
the
prey
are
killed
bv
the
vredators
is
e^
x-\
x?
);
62
describes
the
growth rate
of
the
predator population
based
on the
number
of
prey killed (the
efficiency
of
predators
at
converting predators
to
prey);
q
is the
rate
at
which
the
predators die;
r is the
intrinsic
growth rate
of
the
prey population.
The
equations describe
the
rate
of
population growth
(or
decline)
of
each species.
The
rate
of
change
of the
predator population
is the
difference
between
the
rate
of
growth
due to
feeding
on the
prey
and the
rate
of
death.
The
rate
of
change
of
the
prey population
is the
difference
between
the
natural growth rate (which would
govern
in the
absence
of
predators)
and the
death rate
due to
predation.
Define
f : R x
R
2
-»
R
2
by
(f
is
actually independent
of t;
however,
we
include
t as an
independent variable
so
that this example
fits
into
the
general form discussed above). Then, given initial
108
Chapter
4. Essential ordinary differential
equations
10
steps
of
RK4 use 40 evaluations of
f(t,
u).
In
problems of realistic complexity,
the
evaluation
of
f(t,u)
is
the
most expensive
part
of
the
calculation (often f is
defined by a computer simulation
rather
than
a simple algebraic formula),
and
so
a more reasonable comparison of these results would conclude
that
RK4
is
4 times
as efficient as Euler's method for this particular example
and
level of error. Higher-
order methods
tend
to
use enough fewer steps
than
lower-order methods
that
they
are more efficient even though
they
require more work
per
step.
4.4.3 Numerical methods
for
systems
of ODEs
The
numerical methods presented above can
be
applied directly
to
a system
of
ordinary differential equations. Indeed, when
the
system is written in vector form,
the
notation
is virtually identical. We now present
an
example.
Example
4.10.
Consider two species
of
animals that share a habitat, and suppose
one species is prey to the other.
Let
Xl
(t)
be
the population
of
the predator species
at
time
t,
and
let X2(t)
be
the population
of
the prey at the same time. The Lotka-
Volterra predator-prey model for these two populations is
dXl
dt
=
e2
e
l
X
I
X
2 - qXI,
dX2
dt
=
rX2
-
elXIX2,
where
el,
e2, q, r are positive constants. The parameters have the following interpre-
tations:
•
el
describes the attack rate
of
the predators (the rate at which the prey are
killed
by
the predators is
elxlx2);
•
e2
describes the growth rate
of
the predator population based on the number
of
prey killed (the efficiency
of
predators at converting predators to prey);
• q is the rate at which the predators die;
• r
is the intrinsic growth rate
of
the prey population.
The equations describe the rate
of
population growth (or decline)
of
each species.
The rate
of
change
of
the predator population is the difference between the rate
of
growth due to feeding on the prey
and
the rate
of
death. The rate
of
change
of
the prey population is the difference between the natural growth rate (which would
govern
in
the absence
of
predators) and the death rate due to predation.
Define
f : R x R
2
-+
R
2
by
f(t,x)
= [
e2
e
l
X
l
X
2 - qXl ]
rX2
-
elXIX2
(f
is actually independent
of
t;
however, we include t
as
an independent variable
so that this example fits into the general form discussed above). Then, given initial
4.4. Numerical methods
for
initial value problems
109
values
#1,0
and
#2,0
of the
predator
and
prey populations, respectively,
the
IVP
of
interest
is
where
usmg
the RK4
method
described
above,
we
estimated
the
solution
of
(4-31)
on the
time
interval
[0,50].
The
implementation
is
exactly
as
described
in
(4-30),
except
that
now the
various quantities
(lcj,Uj,f(tj,Ui)J
are
vectors.
The
time
step used
was
At =
0.05 (for
a
total
of
1000 steps).
In
Figure
4-4>
w
&
plot
the two
populations
versus
time;
this
graph
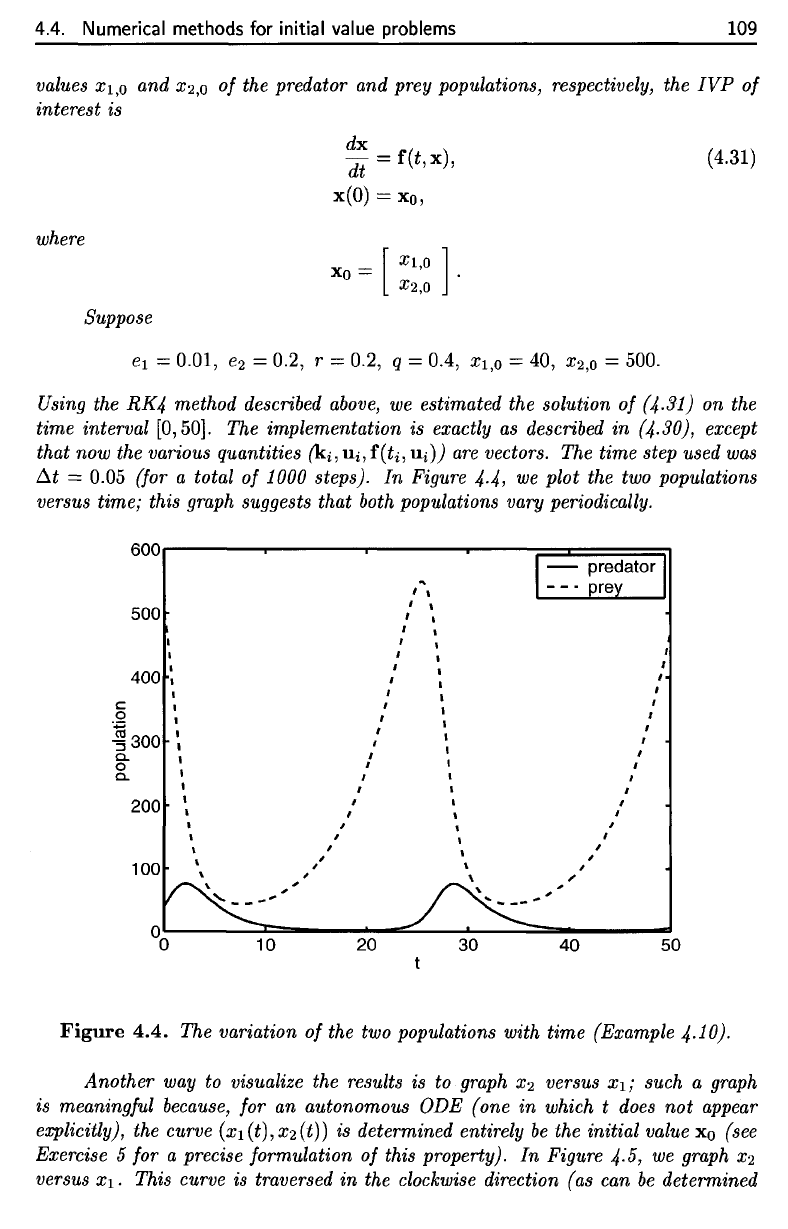
suggests that both populations vary periodically.
Figure
4.4.
The
variation
of
the two
populations with
time
(Example
4-10).
Another
way to
visualize
the
results
is to
graph
x^
versus
x\;
such
a
graph
is
meaningful because,
for an
autonomous
ODE
(one
in
which
t
does
not
appear
explicitly),
the
curve
(xi(t)jX^(t}}
is
determined entirely
be the
initial
value
XQ
(see
Exercise
5 for a
precise formulation
of
this
property).
In
Figure
4-5,
we
graph
x%
versus
x\.
This curve
is
traversed
in the
clockwise direction
(as can be
determined
Suppose
e
l
=
0.01,
e
2
=
0.2,
r =
0.2,
q =
0.4,
XI,
Q
= 40,
x
2
,o
=
500.
4.4. Numerical methods for initial value problems 109
values
Xl,O
and
X2,O
of
the predator and prey populations, respectively, the
IVP
of
interest is
dx
dt
=
f(t,x),
(4.31)
x(O) = xo,
where
xo = [
Xl,O
] .
X2,O
Suppose
el
= 0.01,
e2
= 0.2, r = 0.2, q = 0.4,
Xl,O
= 40,
X2,O
= 500.
Using the
RK4
method described above, we estimated the solution
of
(4.31) on the
time
interval [0,50]. The implementation is exactly as described
in
(4.30), except
that now the various quantities
(ki,
Ui,
f(ti'
Ui))
are
vectors. The
time
step used was
Llt = 0.05 (for a total
of
1000 steps).
In
Figure
4.4,
we
plot the two populations
versus time; this graph suggests that both populations vary periodically.
600
500
I
400 :
c
0
~300
c..
0
c..
200
I
I
,
,
,
100
,
,
..
..
10
I
I
I
I
20
I
I
"'
I ,
I
I
,
,
/
..
I
,
,
I
I
I
I
I
I
I
I
40 50
Figure
4.4.
The variation
of
the two populations with
time
(Example 4.10).
Another
way to visualize the results is to graph
X2
versus
Xl;
such a graph
is meaningful because, for an autonomous
ODE
(one
in
which t does
not
appear
explicitly), the curve
(Xl
(t),
X2
(t)) is determined entirely
be
the initial value xo (see
Exercise
5 for a precise formulation
of
this property).
In
Figure 4.5, we graph
X2
versus
Xl.
This curve is traversed
in
the clockwise direction (as can
be
determined
110
Chapter
4.
Essential ordinary differential equations
by
comparing
with
Figure
4-4)-
F°
r
example, when
the
prey population
is
large
and
the
predator population
is
small (the
upper
left
part
of the
curve),
the
predator
population
will
begin
to
grow.
As it
does,
the
prey population
begins
to
decrease
(since
more prey
are
eaten).
Eventually,
the
prey population gets small enough that
it
cannot
support
a
large
number
of
predators
(far
right part
of the
curve),
and the
predator
population
decreases
rapidly.
When
the
predator population gets small,
the
prey
population
begins
to
grow,
and the
whole
cycle
begins
again.
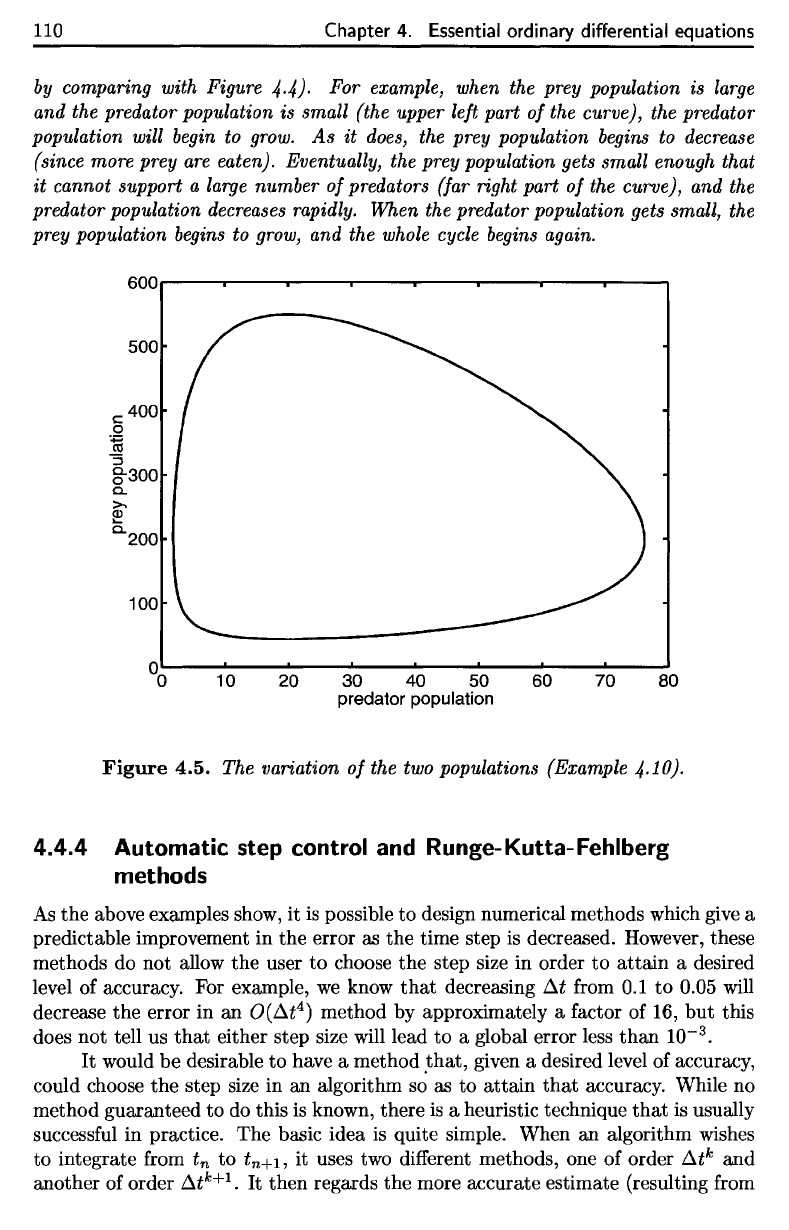
Figure
4.5.
The
variation
of
the two
populations
(Example
4-10).
4.4.4
Automatic
step
control
and
Runge-Kutta-Fehlberg
methods
As
the
above examples show,
it is
possible
to
design numerical methods which give
a
predictable improvement
in the
error
as the
time step
is
decreased. However, these
methods
do not
allow
the
user
to
choose
the
step size
in
order
to
attain
a
desired
level
of
accuracy.
For
example,
we
know
that
decreasing
At
from
0.1 to
0.05
will
decrease
the
error
in an
0(At
4
)
method
by
approximately
a
factor
of 16, but
this
does
not
tell
us
that
either step size
will
lead
to a
global error less
than
10~
3
.
It
would
be
desirable
to
have
a
method
that,
given
a
desired level
of
accuracy,
could
choose
the
step
size
in an
algorithm
so as to
attain
that
accuracy. While
no
method guaranteed
to do
this
is
known, there
is a
heuristic technique
that
is
usually
successful
in
practice.
The
basic idea
is
quite simple. When
an
algorithm wishes
to
integrate
from
t
n
to
t
n+
i,
it
uses
two
different
methods,
one of
order
Ai
fe
and
another
of
order
A£
fc+1
.
It
then regards
the
more accurate estimate (resulting
from
110 Chapter
4.
Essential ordinary differential equations
by comparing with Figure
4.4}.
For example, when the prey population is large
and the predator population is small (the upper left part
of
the curve), the predator
population will begin to grow.
As
it
does, the prey population begins to decrease
(since more prey
are
eaten). Eventually, the prey population gets small enough that
it
cannot support a large number
of
predators (far right part
of
the curve), and the
predator population decreases rapidly. 'When the predator population gets small, the
prey population begins to grow, and the whole cycle begins again.
600r---~----'---~~---r----~--~----~--~
10
20
30 40 50
predator population
60
70
80
Figure
4.5.
The variation
of
the two populations (Example 4.10).
4.4.4 Automatic step control and Runge-Kutta-Fehlberg
methods
As
the above examples show, it
is
possible
to
design numerical methods which give a
predictable improvement in the error as
the
time step
is
decreased. However, these
methods do not allow the user
to
choose
the
step size in order
to
attain
a desired
level of accuracy. For example,
we
know
that
decreasing
D..t
from
0.1
to
0.05 will
decrease
the
error in an
O(D..t4)
method by approximately a factor of 16,
but
this
does
not
tell us
that
either step size will lead to a global error less
than
10-
3
.
It
would be desirable to have a method .that, given a desired level of accuracy,
could choose the step size in an algorithm so as
to
attain
that
accuracy. While no
method guaranteed to do this
is
known, there
is
a heuristic technique
that
is usually
successful in practice. The basic idea
is
quite simple. When an algorithm wishes
to
integrate from tn
to
tn+!, it uses two different methods, one of order
D..t
k
and
another of order
D..t
k
+!.
It
then regards the more accurate estimate (resulting from

4.4. Numerical methods
for
initial
value problems
111
the
O(At
fe+1
)
method)
as the
exact
value,
and
compares
it
with
the
estimate
from
the
lower-order method.
If the
difference
is
sufficiently
small, then
it is
assumed
that
the
step size
is
sufficiently
small,
and the
step
is
accepted. (Moreover,
if the
difference
is too
small, then
it is
assumed
that
the
step size
is
smaller than
it
needs
to be, and it may be
increased
on the
next step.)
On the
other hand,
if the
difference
is
too
large, then
it is
assumed
that
the
step
is
inaccurate.
The
step
is
rejected,
and
At,
the
step
size,
is
reduced. This
is
called automatic
step
control,
and it
leads
to
an
approximate solution computed
on an
irregular grid, since
At can
vary
from
one
step
to the
next. This technique
is not
guaranteed
to
produce
a
global error below
the
desired level, since
the
method only controls
the
local
error
(the error resulting
from
a
single
step
of the
method). However,
the
relationship between
the
local
and
global error
is
understood
in
principle,
and
this understanding leads
to
methods
that
usually achieve
the
desired accuracy.
A
popular class
of
methods
for
automatic step control consists
of the
Runge-
Kutta-Fehlberg
(RKF) methods, which
use two RK
methods together
to
control
the
local error
as
described
in the
previous
paragraph.
The
general
form
of RK
methods,
given
in
(4.29),
shows
that
there
are
many possible
RK
formulas;
indeed,
for
a
given order
At
fc
,
there
are
many
different
RK
methods
that
can be
derived.
This
fact
is
used
in the RKF
methodology
to
choose pairs
of
formulas
that
evaluate
/, the
function
defining
the
ODE,
as few
times
as
possible.
For
example,
it can be
proved
that
every
RK
method
of
order
At
5
requires
at
least
six
evaluations
of /.
It is
possible
to
choose
six
points (i.e.
the
values
ti,ti
+
72/1,...
,tj
+
^h
in
(4.29))
so
that
five of the
points
can be
used
in an
O(At
4
)
formula, and the six
points
together
define
an
O(At
5
)
formula.
(One such pair
of
formulas
is the
basis
of the
popular RKF45 method.) This allows
a
very
efficient
implementation
of
automatic
step
control.
Exercises
1. The
purpose
of
this exercise
is to
estimate
the
value
of
u(0.5),
where
u(t)
is
the
solution
of the
IVP
The
solution
is
w(t)
= te*, and so
w(0.5)
=
e
1
/
2
/2
=
0.82436.
(a)
Estimate
w(0.5)
by
taking
4
steps
of
Euler's
method.
(b)
Estimate
w(0.5)
by
taking
2
steps
of the
improved Euler's method.
(c)
Estimate
w(0.5)
by
taking
1
step
of the
classical fourth-order
RK
method.
Which
estimate
is
more accurate?
How
many times
did
each evaluate
f(t,
u)
=
u
+
e
te
?
2.
Reproduce
the
results
of
Example 4.10.
4.4. Numerical methods for initial value problems
111
the
O(~tk+l)
method) as the exact value, and compares
it
with the estimate from
the lower-order method.
If
the difference
is
sufficiently small,
then
it
is
assumed
that
the step size
is
sufficiently small, and the step
is
accepted. (Moreover, if the
difference
is
too small, then
it
is
assumed
that
the step size
is
smaller
than
it
needs
to
be, and it may be increased on the next step.) On the other hand, if the difference
is
too large,
then
it
is
assumed
that
the step
is
inaccurate. The step
is
rejected, and
~t,
the step size,
is
reduced. This
is
called automatic step control, and
it
leads to
an
approximate solution computed on
an
irregular grid, since
~t
can vary from one
step
to
the
next. This technique
is
not guaranteed
to
produce a global error below
the desired level, since the method only controls the
local error (the error resulting
from a single step of the method). However, the relationship between the local and
global error
is
understood in principle, and this understanding leads to methods
that
usually achieve the desired accuracy.
A popular class of methods for automatic step control consists of the
Runge-
Kutta-Fehlberg (RKF) methods, which use two RK methods together
to
control
the local error as described in the previous paragraph. The general form of RK
methods, given in (4.29), shows
that
there are many possible RK formulas; indeed,
for a given order
!ltk,
there are many different RK methods
that
can be derived.
This fact
is
used in the
RKF
methodology to choose pairs of formulas
that
evaluate
f,
the
function defining the ODE, as
few
times as possible. For example, it can be
proved
that
every RK method of order
!lt
5
requires
at
least six evaluations of f.
It
is
possible to choose six points
(Le.
the values
ti,
ti
+ 12h,
...
,
ti
+ 16h in (4.29))
so
that
five
of
the
points can be used in
an
O(
!lt
4
)
formula, and
the
six points
together define
an
O(!lt
5
)
formula. (One such pair of formulas
is
the basis of the
popular RKF45 method.) This allows a very efficient implementation of automatic
step control.
Exercises
1.
The purpose of this exercise
is
to estimate
the
value of u(0.5), where
u(t)
is
the solution of the
IVP
du t
dt = u + e ,
u(O)
=
O.
(4.32)
The
solution
is
u(t)
= te
t
,
and
so
u(0.5) = e
1
/
2
/2
==
0.82436.
(a) Estimate
u(0.5) by taking 4 steps of Euler's method.
(b) Estimate
u(0.5) by taking 2 steps of the improved Euler's method.
(c)
Estimate u(0.5) by taking 1 step of the classical fourth-order RK method.
Which estimate
is
more accurate?
How
many times did each evaluate f(t,
u)
=
u+
e
t
?
2.
Reproduce
the
results of Example 4.10.

112
Chapter
4.
Essential ordinary
differential
equations
3.
17
The
system
of
ODEs
models
the
orbit
of a
satellite about
two
heavenly bodies,
which
we
will
assume
to be the
earth
and the
moon.
In
these equations,
(x(t),y(t))
are the
coordinates
of the
satellite
at
time
t.
The
origin
of the
coordinate system
is the
center
of
mass
of the
earth-moon
system,
and the
ar-axis
is the
line through
the
centers
of the
earth
and the
moon.
The
center
of the
moon
is at the
point
(1
—
/^i,0)
and the
center
of
the
earth
is at
(—//i,
0),
where
IJL\
=
1/82.45
is the
ratio
of
mass
of the
moon
to the
mass
of the
earth.
The
unit
of
length
is the
distance
from
the
center
of
the
earth
to the
center
of the
moon.
We
write
^2
= 1
—
A*i
•
If
the
satellite satisfies
the
following
initial conditions, then
its
orbit
is
known
to be
periodic with period
T =
6.19216933:
17
Adapted
from
[16],
pages 153-154.
18
Both
MATLAB
and
Mathematica
provide such routines,
ode45
and
NDSolve,
respectively.
19
It
is
easy
to
determine
the
number
of
steps used
by
MATLAB's
ode45
routine.
It is
possible
but
tricky
to
determine
the
number
of
steps used
by
Mathematica's
NDSolve
routine.
where
(a)
Convert
the
system (4.33)
of
second-order ODEs
to a first-order
system.
(b)
Use a
program
that
implements
an
adaptive (automatic step control)
method
18
(such
as
RKF45)
to
follow
the
orbit
for one
period.
Plot
the
orbit
in the
plane,
and
make sure
that
the
tolerance used
by the
adaptive
algorithm
is
small enough
that
the
orbit really appears
in the
plot
to be
periodic.
Explain
the
variation
in
time steps with
reference
to the
motion
of
the
satellite.
(c)
Assume
that,
in
order
to
obtain comparable accuracy with
a fixed
step
size,
it is
necessary
to use the
minimum step chosen
by the
adaptive
algorithm.
How
many steps would
be
required
by an
algorithm with
fixed
step
size?
How
many steps were used
by the
adaptive
algorithm?
19
112
Chapter
4.
Essential ordinary differential equations
3.
17 The system of ODEs
where
/-LI(X
-
/-L2)
T2(X,y)3
/-LlY
T2(X,y)3'
TI
(X,y) =
V(X
+
/-LI)2
+ y2,
T2(X,y)
=
V(X
-
/-L2)2
+ y2,
(4.33)
models
the
orbit of a satellite about two heavenly bodies, which
we
will assume
to
be
the
earth
and
the moon.
In these equations,
(x(t),y(t)) are
the
coordinates of the satellite
at
time t.
The origin of
the
coordinate system
is
the
center of mass of
the
earth-moon
system, and
the
x-axis is
the
line through
the
centers of the earth
and
the
moon. The center of the moon
is
at
the
point
(1
-
/-LI,O)
and
the
center of
the
earth
is
at
(-
/-LI,
0), where
/-LI
= 1/82.45 is
the
ratio of mass of the moon
to
the
mass of the earth. The unit of length
is
the
distance from
the
center
of the
earth
to
the center of the moon.
We
write
/-L2
= 1 -
/-L1.
If
the
satellite satisfies the following initial conditions, then its orbit
is
known
to
be periodic with period T = 6.19216933:
dx
x(O)
= 1.2, dt (0) = 0,
y(O)
= 0,
~~
(0) = -1.04935751.
(a) Convert the system (4.33) of second-order ODEs to a first-order system.
(b) Use a program
that
implements an adaptive (automatic step control)
method
18
(such as RKF45)
to
follow
the
orbit for one period.
Plot
the
orbit in the plane,
and
make sure
that
the tolerance used by the adaptive
algorithm
is
small enough
that
the orbit really appears in the plot
to
be
periodic. Explain the variation in time steps with reference to
the
motion
of the satellite.
(c)
Assume
that,
in order to obtain comparable accuracy with a fixed step
size, it
is
necessary
to
use the minimum step chosen by the adaptive
algorithm.
How
many steps would be required by an algorithm with
fixed step size?
How
many steps were used by the adaptive algorithm?19
17
Adapted
from [16], pages 153-154.
18Both MATLAB
and
Mathematica provide such routines,
ode45
and
NDSolve,
respectively.
19It is easy
to
determine
the
number
of
steps used
by
MATLAB's
ode45
routine.
It
is possible
but
tricky
to
determine
the
number
of
steps
used by Mathematica's
NDSolve
routine.

4.4. Numerical methods
for
initial
value problems
113
4.
Let
The
problem
is to
produce
a
graph,
on the
interval
[0,20],
of the two
compo-
nents
of the
solution
to
where
(a)
Use the RK4
method with
a
step
size
of
At
=
0.1
to
compute
the
solution.
Graph both components
on the
interval
[0,20].
(b)
Use the
techniques
of the
previous section
to
compute
the
exact solution.
Graph
both
components
on the
interval
[0,20].
(c)
Explain
the
difference.
5. (a)
Suppose
t
0
G
[a,
&]
and f :
R
n
->•
R
n
,
u
: [a, 6]
->•
R
n
satisfy
satisfies
Moreover,
show
that
the
curves
and
are the
same.
(b)
Show,
by
producing
an
explicit example
(a
scalar
IVP
will
do),
that
the
above property does
not
hold
for a
differential
equation
that
depends
explicitly
on t
(that
is, for a
nonautonomous
ODE).
4.4. Numerical methods for initial value problems
113
4.
Let
A=![ll
48]
5
48
39
.
The problem
is
to
produce a graph, on
the
interval [0,20], of
the
two compo-
nents of
the
solution to
du
dt =
Au,
(4.34)
u(O)
=
110,
where
(a) Use the RK4 method with a step size of
Llt = 0.1 to compute
the
solution.
Graph
both
components on the interval [0,20].
(b) Use the techniques of the previous section
to
compute the exact solution.
Graph
both
components on
the
interval [0,20].
(c)
Explain the difference.
5.
(a) Suppose
to
E
[a,
b]
and
f:
Rll
-t
Rll,
u :
[a,
b]-t
Rll
satisfy
du
dt =
f(u),
u(t
o
)
=
Uo·
Show
that
v :
[a
+ (it - to), b +
(h
-
to)]
-t
Rll
defined by
v(t) =
u(t
- (tl -
to))
satisfies
dv
dt =
f(v),
v(td
=
110·
Moreover, show
that
the curves
{u(t) tE[a,b]}
and
{v(t) t E
[a
+ (tl -
to),
b + (tl - to)]}
are
the
same.
(b) Show, by producing
an
explicit example (a scalar IVP will do),
that
the
above property does not hold for a differential equation
that
depends
explicitly on
t (that is, for a nonautonomous ODE).

114
Chapter
4.
Essential ordinary differential equations
(a)
Use the RK4
method with step sizes
1/4,1/8,1/16,1/32,1/64,
and
1/128
to
estimate
x(l/2)
and
verify
that
the
error
is
O(Af
4
).
(b)
Use the RK4
method with
step
sizes
1/4,1/8,1/16,1/32,1/64,
and
1/128
to
estimate
x(2).
Is the
error
O(A£
4
)
in
this case
as
well?
If
not, speculate
as to why it is
not.
8. Let
(a)
Solve
the
problem using
the RK4
method
(in floating
point arithmetic)
and
graph
the
results.
(b)
What
is the
exact solution?
(c)
Why is
there
a
discrepancy between
the
computed solution
and the
exact
solution?
(d)
Can
this discrepancy
be
eliminated
by
decreasing
the
step size
in the
RK4
method?
7.
Consider
the
IVP
6.
Consider
the IVP
Use
both Euler's method
and the
improved
Euler
method
to
estimate
#(10),
using step sizes
1,1/2,1/4,1/8,
and
1/16.
Verify
that
the
error
in
Euler's
method
is
O(A£),
while
the
error
in the
improved Euler method
is
O(Ai
2
).
The
matrix
A has an
eigenvalue
A
=
—0.187;
let x be a
corresponding eigen-
vector.
The
problem
is to
produce
a
graph
on the
interval
[0,20]
of the five
components
of the
solution
to
114
Chapter
4.
Essential ordinary differential equations
6. Consider the IVP
dx
dt
= cos
(t)x,
x(O)
=
1.
Use
both
Euler's method and
the
improved Euler method to estimate x(lO),
using step sizes
1,1/2,1/4,1/8,
and 1/16. Verify
that
the error in Euler's
method
is
O(~t),
while
the
error in the improved Euler method
is
O(~t2).
7.
Consider the IVP
dx
- =
1+
lx-II
dt '
x(O)
=
O.
(a) Use the RK4 method with step sizes
1/4,1/8,1/16,1/32,1/64,
and 1/128
to
estimate
x(1/2)
and
verify
that
the error
is
O(~t4).
(b) Use the RK4 method with step sizes
1/4,1/8,1/16,1/32,1/64,
and 1/128
to
estimate
x(2).
Is the error
O(~t4)
in this case as well?
If
not, speculate
as
to
why
it
is
not.
8.
Let
[
-2
1
o 1
-31
A~
l
0
o
-1
2
0
-1
1
-1
.
-1
1 0 0
-3
2
-1
0-2
The
matrix A has
an
eigenvalue A
==
-0.187; let x
be
a corresponding eigen-
vector.
The
problem
is
to produce a graph on the interval [0,20] of the
five
components of
the
solution
to
du
dt
=
Au,
u(O)
= x.
(a) Solve the problem using the RK4 method (in floating point arithmetic)
and graph the results.
(b)
What
is
the exact solution?
(c) Why
is
there a discrepancy between
the
computed solution and
the
exact
solution?
(d) Can this discrepancy be eliminated by decreasing
the
step size in the
RK4 method?
4.5.
Stiff
systems
of
ODEs
115
4.5
Stiff
systems
of
ODEs
The
numerical methods described
in the
last
section, while
adequate
for
many
IVPs,
can be
unnecessarily
inefficient
for
some problems.
We
begin with
a
comparison
of
two
IVPs,
and the
performance
of a
state-of-the-art
automatic
step-control algo-
rithm
on
them.
Example
4.11.
We
consider
the
following
two
IVPs:
We
will
describe
the
matrices
AI
and
A
2
by
their
spectral
decompositions.
The two
matrices
are
symmetric, with
the
same eigenvectors
but
different
eigenvalues.
The
eigenvectors
are
We
solved
both
systems using
the
MATLAB command
ode45,
which implements
a
state-of-the-art
automatic step-control algorithm
based
on a
fourth-fifth-order
scheme.
20
The
results
are
graphed
in
Figure
4-6,
where,
as
expected,
we see
that
the two
com-
puted solutions
are the
same
(or at
least very
similar).
However,
examining
the
results
of the
computations
performed
by
ode45
re-
veals
a
surprise:
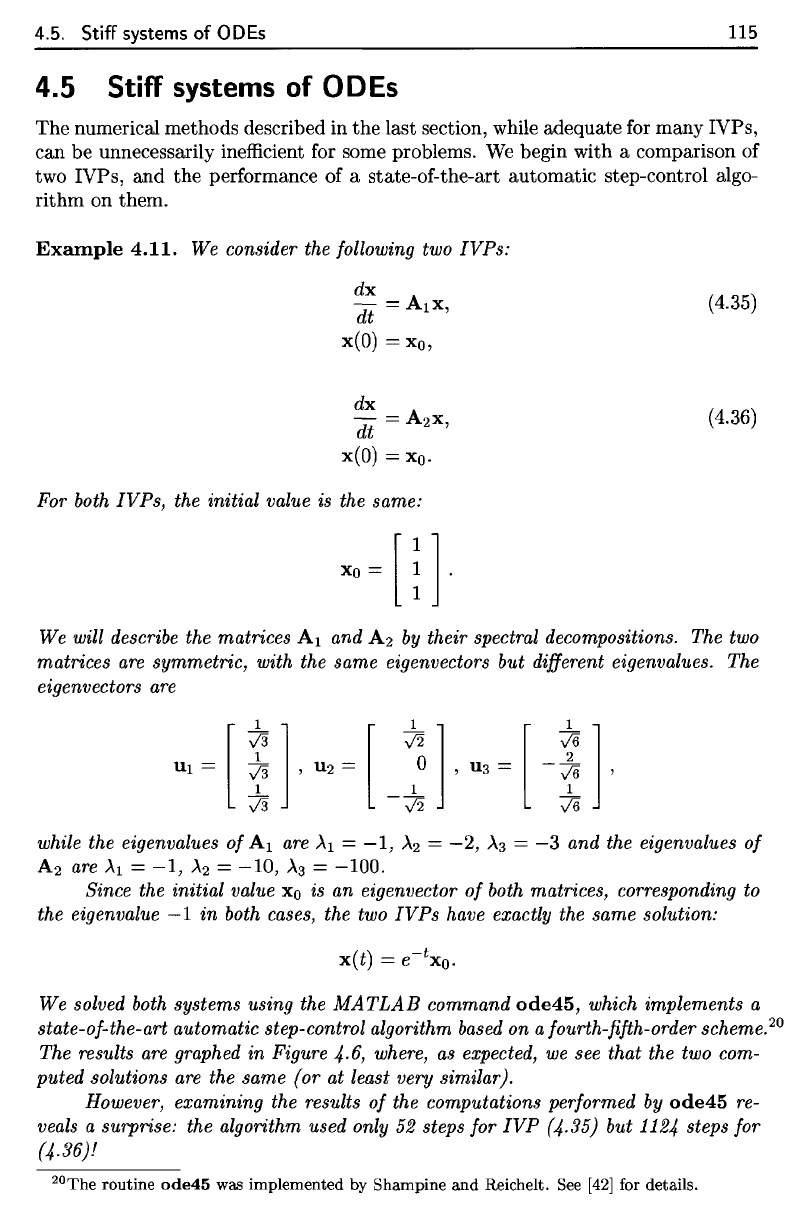
the
algorithm
used
only
52
steps
for
IVP
(4-35)
but
1124
steps
for
(4-36)1
20
The
routine
ode45
was
implemented
by
Shampine
and
Reichelt.
See
[42]
for
details.
For
both
IVPs,
the
initial value
is the
same:
while
the
eigenvalues
of
AI
are
AI
=
—I,
A
2
=
—1,
X
3
=
—3
and the
eigenvalues
of
A
2
are
AI
=
-I,
A
2
=
-10,
A
3
=
-100.
Since
the
initial value
x
0
is an
eigenvector
of
both
matrices,
corresponding
to
the
eigenvalue
—I
in
both
cases,
the two
IVPs have
exactly
the
same solution:
4.5. Stiff systems
of
ODEs
115
4.5 Stiff systems
of
ODEs
The
numerical
methods
described in
the
last section, while
adequate
for
many
IVPs,
can
be
unnecessarily inefficient for some problems. We begin
with
a comparison of
two IVPs,
and
the
performance
of
a state-of-the-art
automatic
step-control algo-
rithm
on
them.
Example
4.11.
We consider the following two IVPs:
dx
dt =
Alx,
x(O)
=
Xo,
dx
dt = A
2
x,
x(O)
=
Xo.
For both IVPs, the initial value is the same:
(4.35)
(4.36)
We will describe the matrices
Al
and A2
by
their spectral decompositions. The two
matrices
are
symmetric, with the same eigenvectors but different eigenvalues. The
eigenvectors
are
while the eigenvalues
of
Al
are
Al
=
-1,
A2
=
-2,
A3
=
-3
and the eigenvalues
of
A2
are
Al
=
-1,
A2
=
-10,
A3
=
-100.
Since the initial value
Xo
is an eigenvector
of
both matrices, corresponding to
the eigenvalue
-1
in
both cases, the two
IVPs
have exactly the same solution:
We solved both systems using the
MATLAB
command
ode45,
which implements a
state-of-the-art automatic step-control algorithm based on a fourth-fifth-order scheme.
2o
The results
are
graphed in Figure 4.6, where,
as
expected,
we
see that the two com-
puted solutions
are
the same (or at least very similar).
However, examining the results
of
the computations performed by
ode45
re-
veals a surprise: the algorithm used only 52 steps for
IVP
(4.35) but 1124 steps for
(4·36)!
20The
routine
ode45
was
implemented
by
Shampine
and
Reichelt. See
[42]
for details.
116
Chapter
4.
Essential ordinary differential equations
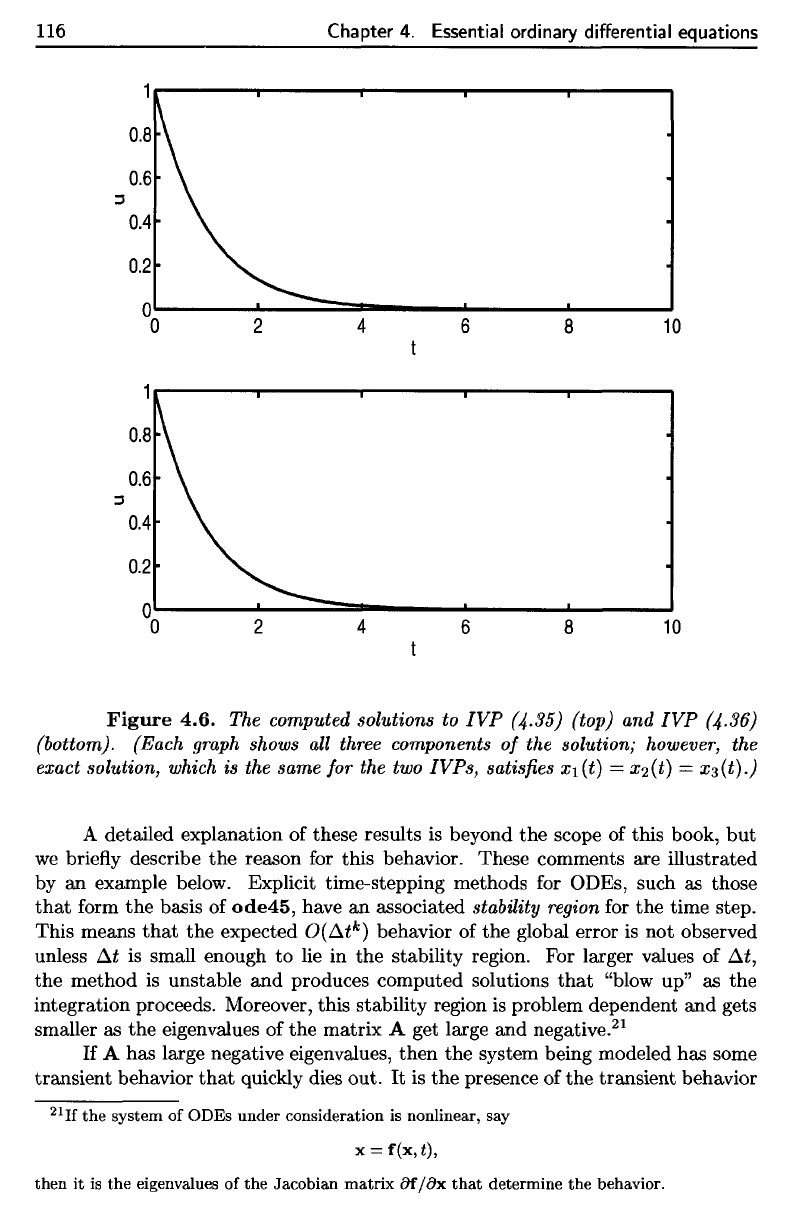
Figure
4.6.
The
computed
solutions
to
IVP
(4.35)
(top)
and
IVP
(4-36)
(bottom).
(Each
graph
shows
all
three
components
of the
solution; however,
the
exact
solution,
which
is the
same
for the two
IVPs,
satisfies
xi(t]
=
£
2
(£)
=
xs(t)•)
A
detailed
explanation
of
these results
is
beyond
the
scope
of
this
book,
but
we
briefly
describe
the
reason
for
this behavior. These comments
are
illustrated
by
an
example below. Explicit time-stepping methods
for
ODEs, such
as
those
that
form
the
basis
of
ode45,
have
an
associated stability
region
for the
time step.
This means
that
the
expected
O(At
fc
)
behavior
of the
global error
is not
observed
unless
A£
is
small enough
to lie in the
stability region.
For
larger values
of
At,
the
method
is
unstable
and
produces computed solutions
that
"blow
up" as the
integration proceeds. Moreover, this stability region
is
problem dependent
and
gets
smaller
as the
eigenvalues
of the
matrix
A get
large
and
negative.
21
If
A has
large negative eigenvalues, then
the
system being modeled
has
some
transient
behavior
that
quickly dies out.
It is the
presence
of the
transient
behavior
then
it is the
eigenvalues
of the
Jacobian matrix
df/dx
that determine
the
behavior.
21
If the
system
of
ODEs under consideration
is
nonlinear,
say
116
Chapter
4. Essential ordinary differential equations
2 4
6 8
10
2 4
6
8
10
Figure
4.6.
The computed solutions to
IVP
(4.35) (top) and
IVP
(4.36)
(bottom). (Each graph shows all three components
of
the solution; however, the
exact solution, which is the same for the two IVPs, satisfies Xl(t) = X2(t) = X3(t).)
A detailed explanation of these results
is
beyond
the
scope of this book,
but
we
briefly describe
the
reason for this behavior. These comments are illustrated
by an example below. Explicit time-stepping methods for ODEs, such as those
that
form
the
basis of
ode45,
have
an
associated stability region for
the
time step.
This means
that
the
expected
O(~tk)
behavior of the global error
is
not observed
unless
~t
is
small enough to lie in
the
stability region. For larger values of
~t,
the method
is
unstable
and
produces computed solutions
that
"blow up" as the
integration proceeds. Moreover, this stability region
is
problem dependent and gets
smaller as the eigenvalues of the matrix A get large and negative.
21
If
A has large negative eigenvalues, then the system being modeled has some
transient behavior
that
quickly dies out.
It
is
the
presence of
the
transient behavior
21
If
the
system
of
ODEs
under
consideration is nonlinear, say
x =
f(x,t),
then
it
is
the
eigenvalues
of
the
Jacobian
matrix
8f
/
ax
that
determine
the
behavior.

4.5.
Stiff
systems
of
ODEs
117
that
requires
a
small time
step—initially,
the
solution
is
changing over
a
very small
time scale,
and the
time step must
be
small
to
model this behavior accurately.
If,
at the
same time, there
are
small negative eigenvalues, then
the
system also
models components
that
die out
more slowly. Once
the
transients have died out,
one
ought
to be
able
to
increase
the
time
step
to
model
the
more slowly varying
components
of the
solution. However, this
is the
weakness
of
explicit methods like
Euler's method, RK4,
and
others:
the
transient behavior inherent
in the
system
haunts
the
numerical method even when
the
transient
components
of the
solution
have died out.
A
time step
that
ought
to be
small enough
to
accurately
follow
the
slowly
varying components produces instability
in the
numerical method
and
ruins
the
computed solution.
A
system with negative eigenvalues
of
widely
different
magnitudes (that
is, a
system
that
models components
that
decay
at
greatly
different
rates)
is
sometimes
called
stiff.
22
Stiff
problems require special numerical methods;
we
give examples
below
in
Section 4.5.2. First, however,
we
discuss
a
simple example
for
which
the
ideas presented above
can be
easily understood.
4.5.1
A
simple
example
of a
stiff
system
The
IVP
has
solution
and the
system
qualifies
as
stiff
according
to the
description given above.
We
will
apply Euler's method, since
it is
simple enough
that
we can
completely understand
its
behavior. However, similar results would
be
obtained with
RK4 or
another
explicit
method.
To
understand
the
behavior
of
Euler's method
on
(4.37),
we
write
it out ex-
plicitly.
We
have
with
that
is,
22
Stiffness
is a
surprisingly
subtle
concept.
The
definition
we
follow
here
does
not
capture
all of
this
subtlety;
moreover,
there
is not a
single,
well-accepted
definition
of a
stiff
system.
See
[33],
Section
6.2,
for a
discussion
of the
various
definitions
of
stiffness.
4.5. Stiff systems of ODEs
117
that
requires a small time
step-initially,
the solution is changing over a very small
time scale,
and
the
time step must
be
small
to
model this behavior accurately.
If,
at
the
same time, there are small negative eigenvalues,
then
the system also
models components
that
die
out
more slowly. Once
the
transients have died out,
one ought
to
be able
to
increase
the
time step
to
model
the
more slowly varying
components of
the
solution. However, this is
the
weakness of explicit methods like
Euler's method, RK4,
and
others:
the
transient behavior inherent in
the
system
haunts
the
numerical method even when
the
transient components of
the
solution
have died out. A time step
that
ought
to
be small enough
to
accurately follow
the
slowly varying components produces instability in
the
numerical method and ruins
the
computed solution.
A system with negative eigenvalues of widely different magnitudes
(that
is, a
system
that
models components
that
decay
at
greatly different rates) is sometimes
called
stiJJ.22
Stiff problems require special numerical methods;
we
give examples
below in Section 4.5.2. First, however,
we
discuss a simple example for which
the
ideas presented above can be easily understood.
4.5.1 A simple example
of
a stiff system
The
IVP
has solution
d~l
=
-10
7
Ul,
Ul(O)
=
1,
dU2
dt
=
-U2,
U2(0) = 1
(t) = [
ul(0)e-
107t
]
u
u2(0)e-
t
'
(4.37)
and
the system qualifies as stiff according
to
the
description given above.
We
will
apply Euler's method, since
it
is simple enough
that
we
can completely understand
its behavior. However, similar results would be obtained with RK4 or another
explicit method.
To understand
the
behavior of Euler's method on (4.37),
we
write
it
out
ex-
plicitly.
We
have
with
that
is,
U~n+1)
=
u~n)
_
10
7
~tu~n)
=
(1
- 10
7
~t)
u~n),
u~n+1)
=
u~n)
_
~tu~n)
=
(1
-
~t)
u~n).
22Stiffness is a surprisingly subtle concept.
The
definition we follow here does
not
capture
all of
this subtlety; moreover,
there
is not a single, well-accepted definition
of
a stiff system. See
[33],
Section 6.2, for a discussion
of
the
various definitions of stiffness.
