Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


98
Chapter
4.
Essential ordinary
differential
equations
where
The
matrix
A is
symmetric,
and an
orthonormal
basis
for R
2
consists
of
the
vectors
The
solution
is
where
We
obtain
and
Finally,
The
technique
for
solving
(4.20)
presented
in
this section,
which
we
have
described
as a
spectral method,
is
usually
referred
to as the
method
of
variation
of
parameters.
The
corresponding
eigenvalues
are
\i
= 0,
X%
= 2.
We
now
express
f(t)
in
terms
of the
eigenvectors:
98
Chapter
4.
Essential ordinary differential equations
where
A =
[1
1]
f(t)
= [
C?S
(t) ] .
1
l'
sm
(t)
The
matrix A
is
symmetric, and
an
orthonormal
basis
for R2 consists
of
the vectors
U1
= [
_;,
l'
U2
= [
;,
l·
The
corresponding eigenvalues
are
A1
= 0,
A2
=
2.
We
now express
f(t)
in terms
of
the eigenvectors:
The
solution
is
where
We
obtain
and
Finally,
f(t)
= Cl(t)Ul + C2(t)U2,
1 .
Cl(t) =
f(t)
.
U1
=
J2(cos
(t) -
sm
(t)),
1 .
C2(t)
=
f(t)
.
U2
=
J2(cos
(t) +
sm
(t)).
dal 1 .
dt
=
J2
(cos
(t) -
sm
(t)),
a1(0)
= 0,
da2
1 .
dt
=
2a2
+
J2
(cos
(t) +
sm
(t)) ,
a2(0)
=
O.
1
it
aI(t) =
J2
0
{CDS(S)
-sines)}
ds
=
~
(sin (t) + cos (t) -
1)
1
it
a2(t) =
J2
0 e
2
(t-s) {cos
(s)
+ sin (s)}
ds
1 .
=
In
(3e
2t
- 3cos(t) -
sm(t)).
5y2
[
/0
(2cos(t)
+4sin(t)
+3e
2t
-5)
1
x(t)
=
a1
(t)U1 + a2(t)u2 =
110
(-8 cos (t) _ 6 sin (t) +
3e
2t
+
5)
.
The
technique for solving (4.20) presented in
this
section, which we have
described
as
a
spectral
method,
is usually referred
to
as
the
method
of variation of
parameters.

4.3. Linear systems
with
constant coefficients
99
2.
Consider
the
IVP
(4.18),
where
A is the
matrix
in
Example 4.5.
(a)
Explain why,
no
matter what
the
value
of
x
0
,
the
solution
x(£)
converges
to a
constant vector
as t
—>
oo.
(b)
Find
all
values
of
x
0
such
that
the
solution
x is
equal
to a
constant
vector
for
all
values
of t.
3.
Find
the
general solution
to
where
4.
Find
the
general solution
to
where
5.
Let A be the
matrix
in
Exercise
3.
Find
all
values
of
XQ
such
that
the
solution
to
(4.18) decays exponentially
to
zero.
6.
Let A be the
matrix
in
Exercise
4.
Find
all
values
of
XQ
such
that
the
solution
to
(4.18) decays exponentially
to
zero.
7.
Let A be the
matrix
of
Example
4.5.
Solve
the IVP
where
Exercises
1.
Consider
the IVP
(4.18), where
A is the
matrix
in
Example 4.5. Find
the
solution
for
4.3. Linear systems with constant coefficients
99
Exercises
1.
Consider
the
IVP
(4.18), where A
is
the
matrix
in Example 4.5. Find
the
solution for
2.
Consider the
IVP
(4.18), where A
is
the
matrix in Example 4.5.
(a) Explain why, no
matter
what
the
value of xo,
the
solution x(t) converges
to
a constant vector as t
-+
00.
(b) Find all values of
Xo
such
that
the
solution x is equal to a constant vector
for all values of
t.
3. Find
the
general solution
to
dx
dt =
Ax,
where
A=[~
~].
4. Find
the
general solution
to
dx
dt =
Ax,
where
5.
Let A be
the
matrix
in Exercise 3. Find all values of
Xo
such
that
the
solution
to
(4.18) decays exponentially
to
zero.
6.
Let A be
the
matrix
in Exercise 4.
Find
all values of
Xo
such
that
the
solution
to
(4.18) decays exponentially
to
zero.
7.
Let A
be
the
matrix
of Example 4.5. Solve
the
IVP
dx
dt
=
Ax
+
ret),
x(O)
=
0,
where
ret)
= [
~
l.
sin (t)

100
Chapter
4.
Essential ordinary differential equations
Solve
the
IVP
where
Here
o,
6, c, d are
positive constants,
x(t]
is the
population
of the first
species
at
time
£,
and
y(t]
is the
corresponding population
of the
second species
(x
and y are
measured
in
some convenient units,
say
thousands
or
millions
of
animals).
The
equations
are
easy
to
understand: either species increases
(exponentially)
if the
other
is not
present, but, since
the two
species compete
for
the
same resources,
the
presence
of one
species contributes negatively
to
the
growth
rate
of the
other.
(a)
Solve
the IVP
with
6 = c = 2,
o
=
d=l,
x(0)
= 2, and
j/(0)
= 1, and
explain
(in
words)
what happens
to the
populations
of the two
species
in
the
long term.
(b)
With
the
values
of a, 6, c, d
given
in
part
9a, is
there
an
initial condition
which
will
lead
to a
different
(qualitative) outcome?
10.
The
purpose
of
this
exercise
is to
derive
the
solution
(4.11)
of the IVP
The
solution
can be
found
using
the
techniques
of
this
section, although
the
computations
are
more
difficult
than
any of the
examples
we
have presented.
8. Let
9.
The
following
system
has
been proposed
as a
model
of the
population dynam-
ics of two
species
of
animals
that
compete
for the
same resource:
100
Chapter
4.
Essential ordinary differential equations
8. Let
Solve
the
IVP
where
-4
2
2
-4
-4 -4
-4]
-4
.
2
dx
dt =
Ax
+ f(t),
x(o)
= xo,
[
COS
(t) ] [ 1 ]
f(t)
= 1 , Xo = 1 .
sin (t) 1
9.
The
following system has been proposed as a model of the population dynam-
ics of two species of animals
that
compete for
the
same resource:
dx
dt =
ax
-
by,
x(O)
=
Xo,
~~
=
-ex
+ dy,
y(O)
=
yo.
Here
a,
b,
e,
d are positive constants, x(t)
is
the population of the first species
at
time t,
and
yet)
is
the corresponding population
of
the second species
(x
and
y are measured in some convenient units, say thousands or millions
of animals).
The
equations are easy
to
understand: either species increases
(exponentially) if the other
is
not present,
but,
since
the
two species compete
for the same resources,
the
presence of one species contributes negatively
to
the
growth
rate
of the other.
(a) Solve
the
IVP
with b = e =
2,
a = d =
1,
x(O)
=
2,
and
yeO)
=
1,
and
explain (in words) what happens
to
the populations of the two species
in
the
long term.
(b)
With
the
values of
a,
b,
e,
d given in
part
9a,
is
there
an
initial condition
which will lead
to
a different (qualitative) outcome?
10.
The
purpose of this exercise
is
to
derive
the
solution (4.11) of
the
IVP
J2u
2
dt
2
+ B u = J(t),
The
solution
u(to) = 0,
du
dt (to) =
o.
u(t) =
~
rt
sin
(B(t
- 8»J(8)
d8
ito
(4.23)
can
be
found using the techniques of this section, although the computations
are more difficult
than
any of the examples
we
have presented.

4.4
Numerical
methods
for
initial
value problems
So
far in
this
chapter,
we
have discussed simple
classes
of
ODEs,
for
which
it is
possible
to
produce
an
explicit formula
for the
solution. However, most
differential
equations cannot
be
solved
in
this sense. Moreover, sometimes
the
only formula
that
can be
found
is
difficult
to
evaluate, involving integrals
that
cannot
be
computed
in
terms
of
elementary functions, eigenvalues
and
eigenvectors
that
cannot
be
found
exactly,
and so
forth.
In
cases like these,
it may be
that
the
only
way to
investigate
the
solution
is to
approximate
it
using
a
numerical method, which
is
simply
an
algorithm producing
an
approximate solution.
We
emphasize
that
the use of a
numerical method always
implies
that
the
computed solution will
be in
error.
It is
essential
to
know something
about
the
magnitude
of
this error; otherwise,
one
cannot
use the
solution with
any
confidence.
Most numerical methods
for
IVPs
in
ODEs
are
designed
for first-order
scalar
equations. These
can be
applied, almost without change,
to first-order
systems,
and
hence
to
higher-order ODEs (after they have been converted
to first-order
systems).
Therefore,
we
begin
by
discussing
the
general
first-order
scalar
IVP,
which
is of the
form
We
shall discuss time-stepping methods, which seek
to find
approximations
to
n(ti),^(£2),
• • •
,u(t
n
},
where
to <
ti
<
t^
< • • • <
t
n
define
the
grid.
The
quantities
ti
—
to,t2
—
ti,...,
t
n
—
t
n
-i
are
called
the
time steps.
The
basic idea
of
time-stepping methods
is
based
on the
fundamental theorem
of
calculus, which implies
that
if
4.4. Numerical methods
for
initial
value problems
101
(a)
Rewrite (4.23)
in the
form
Notice
that
the
matrix
A is not
symmetric.
(b)
Find
the
eigenvalues
AI,
A2
and
eigenvectors
Ui,u
2
of A.
(c)
Write
the
vector-valued
function
F(t)
in the
form
Since
the
eigenvectors
ui
and
u
2
are not
orthogonal, this
will
require
solving
a (2 x 2)
system
of
equations
to find
c\
(t}
and
c
2
(t).
(d)
Write
the
solution
in the
form
and
solve
the
scalar IVPs
to get
ai
(t},
a
2
(t}.
(e)
The
desired solution
is
u(t]
=
xi(t).
Show
that
the
result
is
(4.11).
4.4. Numerical methods
for
initial value problems
(a) Rewrite (4.23) in the form
dx
dt
=
Ax
+ F(t), x(to) =
O.
Notice
that
the
matrix A
is
not symmetric.
(b) Find the eigenvalues
Al,
A2 and eigenvectors
Ul,
U2
of
A.
(c)
Write
the
vector-valued function F(t) in the form
F(t) =
Cl(t)Ul
+C2(t)U2.
101
Since
the
eigenvectors
Ul
and
U2
are not orthogonal, this will require
solving a
(2
x
2)
system of equations
to
find
Cl(t)
and
C2(t).
(d) Write
the
solution in the form
x(t) =
al(t)ul
+ a2(t)u2,
and
solve the scalar IVPs
to
get al(t), a2(t).
(e)
The desired solution
is
u(t) = Xl(t). Show
that
the
result
is
(4.11).
4.4
Numerical methods for initial value problems
So
far in this chapter,
we
have discussed simple classes of ODEs, for which it
is
possible
to
produce an explicit formula for the solution. However, most differential
equations cannot be solved in this sense. Moreover, sometimes the only formula
that
can be found
is
difficult to evaluate, involving integrals
that
cannot be computed in
terms of elementary functions, eigenvalues and eigenvectors
that
cannot be found
exactly,
and
so forth.
In cases like these, it may be
that
the
only way
to
investigate
the
solution
is
to
approximate it using a
numerical method, which
is
simply an algorithm producing
an approximate solution.
We
emphasize
that
the use of a numerical method always
implies
that
the computed solution will be in error.
It
is essential
to
know something
about
the
magnitude of this error; otherwise, one cannot use the solution with any
confidence.
Most numerical methods for IVPs in ODEs are designed for first-order scalar
equations. These can be applied, almost without change,
to
first-order systems, and
hence
to
higher-order ODEs (after they have been converted to first-order systems).
Therefore,
we
begin by discussing the general first-order scalar IVP, which
is
of the
form
du
dt
=
!(t,
u),
u(t
o
)
=
Uo·
(4.24)
We
shall discuss time-stepping methods, which seek
to
find approximations
to
U(tl),
U(t2),".,
u(t
n
),
where
to
<
tl
<
t2
< ... < tn define
the
grid.
The quantities
it
-
to,
t2
-
tl,···,
tn -
tn-l
are called the time steps.
The basic idea of time-stepping methods
is
based on
the
fundamental theorem
of calculus, which implies
that
if
du
dt (t) =
!(t,u(t)),

Now,
we
cannot
(in
general) hope
to
evaluate
the
integral
in
(4.25) analytically;
however,
any
numerical method
for
approximating
the
value
of a
definite
integral
(such
methods
are
often
referred
to as
quadrature
rules)
can be
adapted
to
form
the
basis
of a
numerical method
of
IVPs.
By the
way, equation
(4.25)
explains
why the
process
of
solving
an
IVP
numerically
is
often referred
to as
integrating
the
ODE.
4.4.1 Euler's method
The
simplest method
of
integrating
an ODE is
based
on the
left-endpoint
rule:
The
reader should notice
that
(except
for i = 0)
there
are two
sources
of
error
in
the
estimate
MJ+I.
First
of
all, there
is the
error inherent
in
using
formula
(4.26)
to
advance
the
integration
by one
time step. Second, there
is the
accumulated error
due to the
fact
that
we do not
know
u(ti]
in
(4.26),
but
rather only
an
approximation
to
it.
The
method
(4.27)
is
referred
to as
Euler's method.
102
Chapter
4.
Essential ordinary differential equations
then
Applying
this
to
(4.25),
we
obtain
Of
course, this
is not a
computable
formula,
because, except possibly
on the first
step
(i = 0), we do not
know
u(ti)
exactly. Instead,
we
have
an
approximation,
Ui
=
u(ti).
Formula
(4.26)
suggests
how to
obtain
an
approximation
m
+
\
to
u(ti
+
i):
Example
4.9. Consider
the IVP
The
exact
solution
is
and
we can use
this formula
to
determine
the
errors
in the
computed
approximation
to
u(t).
Applying
Euler's method with
the
regular
grid
t{
=
iAt,
Ai
=
10/n,
we
have
102
Chapter
4.
Essential ordinary differential equations
then
(4.25)
Now,
we
cannot (in general) hope
to
evaluate the integral in (4.25) analytically;
however, any numerical method for approximating the value of a definite integral
(such methods are often referred
to
as quadrature rules) can be adapted
to
form
the
basis of a numerical method of IVPs. By
the
way,
equation (4.25) explains why the
process of solving an IVP numerically is often referred to as
integrating
the
ODE.
4.4.1 Euler's method
The simplest method of integrating an ODE is based on the left-endpoint rule:
lb
f(x)
dx
==
f(a)(b -
a).
Applying this
to
(4.25),
we
obtain
(4.26)
Of course, this
is
not a computable formula, because, except possibly on the first
step
(i = 0),
we
do not know U(ti) exactly. Instead,
we
have an approximation,
Ui
==
U(ti)' Formula (4.26) suggests how
to
obtain an approximation
Ui+1
to
U(ti+1):
(4.27)
The reader should notice
that
(except for i =
0)
there are two sources of error in
the estimate
UHl.
First of all, there
is
the error inherent in using formula (4.26)
to
advance the integration by one time step. Second, there
is
the accumulated error
due to
the
fact
that
we
do not know
u(
ti) in (4.26),
but
rather only an approximation
to
it.
The method (4.27)
is
referred to as Euler's method.
Example
4.9.
Consider the
IVP
du u
dt I +
t2'
u(O)
= 1.
(4.28)
The exact solution is
u(t)
= e
tan
-
1
t,
and we can use this formula to determine the errors
in
the computed approximation
to
u(t).
Applying Euler's method with the regular grid
ti
= iLlt, Llt =
lOin,
we
have
4.4. Numerical methods
for
initial
value
problems
103
For
example, with
UQ
= 1 and
n
=
100,
we
obtain
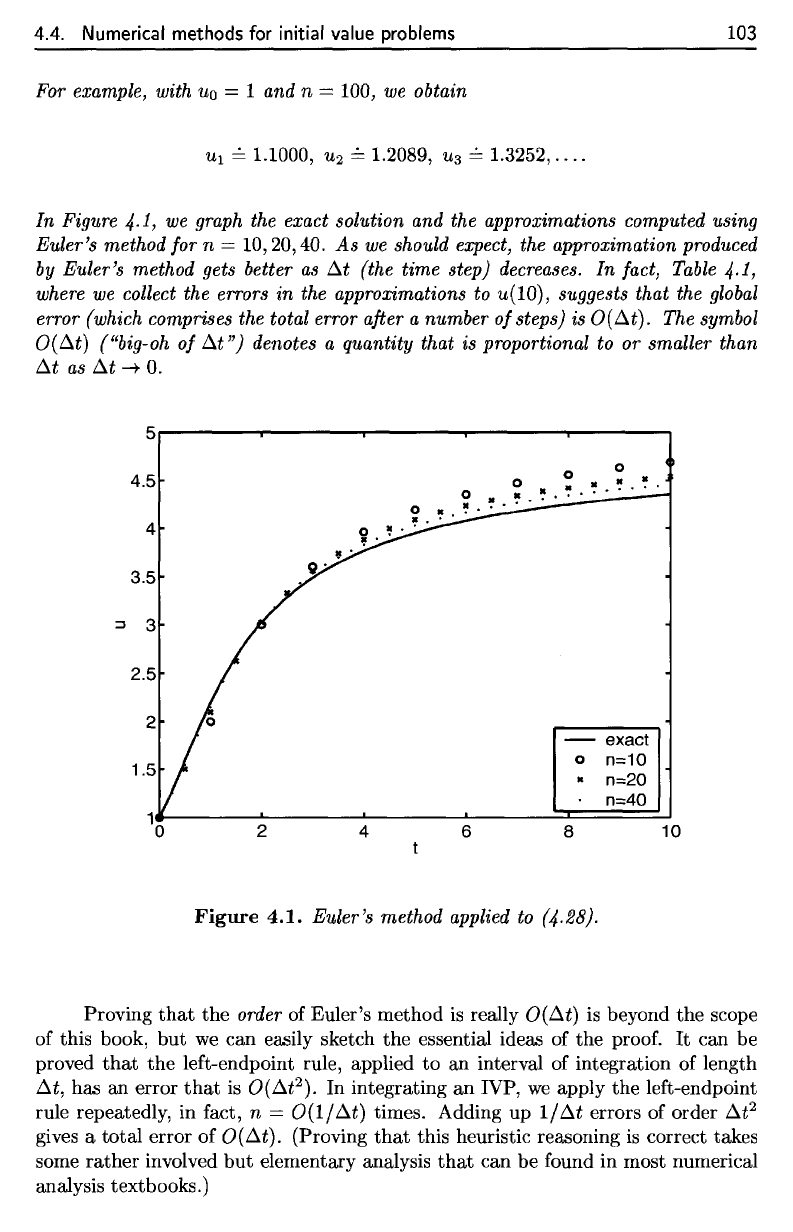
In
Figure
4-1,
we
graph
the
exact solution
and the
approximations
computed
using
Euler's
method
for n
=
10,20,40.
As we
should
expect,
the
approximation
produced
by
Euler's method
gets
better
as At
(the time
step)
decreases.
In
fact,
Table
4-1,
where
we
collect
the
errors
in the
approximations
to
w(10),
suggests
that
the
global
error
(which
comprises
the
total
error
after
a
number
of
steps)
is
O(At).
The
symbol
0(At)
("big-oh
of
At")
denotes
a
quantity that
is
proportional
to or
smaller than
At as
At
->•
0.
Figure
4.1. Euler's method
applied
to
(4-28).
Proving
that
the
order
of
Euler's method
is
really
O(At)
is
beyond
the
scope
of
this
book,
but we can
easily sketch
the
essential
ideas
of the
proof.
It can be
proved
that
the
left-endpoint
rule, applied
to an
interval
of
integration
of
length
At, has an
error
that
is
O(At
2
).
In
integrating
an
IVP,
we
apply
the
left-endpoint
rule
repeatedly,
in
fact,
n =
0(l/At)
times. Adding
up
I/At
errors
of
order
At
2
gives
a
total
error
of
0(At).
(Proving
that
this heuristic reasoning
is
correct takes
some
rather involved
but
elementary analysis
that
can be
found
in
most numerical
analysis textbooks.)
4.4. Numerical methods for initial value problems
103
For example, with
Uo
= 1
and
n = 100,
we
obtain
Ul
~ 1.1000,
U2
~ 1.2089,
U3
~
1.3252,
....
In
Figure
4.1,
we graph the exact solution and the approximations computed using
Euler's method for n
= 10,20,40.
As
we
should expect, the approximation produced
by Euler's method gets better
as
IJ..t
(the
time
step) decreases.
In
fact, Table 4.1,
where
we
collect the errors
in
the approximations to u(10), suggests that the global
error (which comprises the total error after a number
of
steps) is O(lJ..t). The symbol
O(lJ..t) ("big-oh
of
IJ..t")
denotes a quantity that is proportional to or smaller than
IJ..t
as
IJ..t
~
O.
5~------~-------r------~--------~------,
4.5
4
3.5
:::J
3
2.5
2
2 4
o
o
~.
I!.
~
.
~
".!,.
'!
.....
~.
I!
....
,
..
6
- exact
o n=10
It
n=20
n=40
8
Figure
4.1.
Euler's method applied to (4.28).
10
Proving
that
the
order of Euler's
method
is
really O(lJ..t) is beyond
the
scope
of
this book,
but
we
can easily sketch
the
essential ideas
of
the
proof.
It
can be
proved
that
the
left-endpoint rule, applied
to
an
interval
of
integration of length
IJ..t,
has
an
error
that
is 0(lJ..t
2
).
In integrating
an
IVP,
we
apply
the
left-endpoint
rule repeatedly, in fact, n =
0(1/
IJ..t)
times. Adding
up
1/
IJ..t
errors
of
order
IJ..t
2
gives a
total
error
of
O(lJ..t). (Proving
that
this heuristic reasoning
is
correct takes
some
rather
involved
but
elementary analysis
that
can
be
found
in
most numerical
analysis textbooks.)

104
Chapter
4.
Essential ordinary differential equations
n
10
20
40
80
160
320
640
Error
in
w(10)
-3.3384
•
1Q-
1
-1.8507
-KT
1
-1.0054
-HT
1
-5.2790
•
1Q-
2
-2.7111
-1Q-
2
-1.3748
-HT
2
-6.9235
•
10~
3
Error
in
w(io)
At
-3.3384
•
1Q-
1
-3.7014
-10-
1
-4.0218
-HT
1
-4.2232
-
HT
1
-4.3378
•
lO"
1
-4.3992
•
1Q-
1
-4.4310
•
1Q-
1
Table
4.1.
Global
error
in
Euler's
method
for
(4-28).
4.4.2
Improving
on
Euler's
method:
Runge-Kutta
methods
If
the
results suggested
in the
previous section
are
correct, Euler's method
can
be
used
to
approximate
the
solution
to an
IVP
to any
desired accuracy
by
simply
making
At
small enough. Although this
is
true (with certain restrictions),
we
might
hope
for a
more
efficient
method—one
that
would
not
require
as
many time
steps
to
achieve
a
given accuracy.
To
improve Euler's method,
we
choose
a
numerical integration technique
that
is
more accurate
than
the
left-endpoint
rule.
The
simplest
is the
midpoint
rule:
If
At
= b
—
a
(and
the
integrand
/ is
sufficiently
smooth), then
the
error
in the
midpoint rule
is
O(A£
3
).
Following
the
reasoning
in the
previous section,
we
expect
that
the
corresponding method
for
integrating
an IVP
would
have
O(A£
2
)
global
error.
It is not
immediately clear
how to use the
midpoint rule
for
quadrature
to
integrate
an
IVP.
The
obvious equation
is
Putting this approximation together with
the
midpoint rule,
and
using
the
approx-
imation
Ui
=
u(ti),
we
obtain
the
improved
Euler
method:
However,
after
reaching time
ti in the
integration,
we
have
an
approximation
for
u(ti),
but
none
for
u(ti
+
A£/2).
To use the
midpoint rule requires
that
we first
generate
an
approximation
for
u(ti
+
Ai/2);
the
simplest
way to do
this
is
with
an
Euler step:
104
Chapter
4. Essential ordinary differential equations
n
Error
in u(10)
Error
in
u(10)
At
10
-3.3384.10-
1
-3.3384.
10-
1
20
-1.8507.10-
1
-3.7014.10-
1
40
-1.0054.10-
1
-4.0218.
10-
1
80
-5.2790·
10-
2
-4.2232 .
10-
1
160
-2.7111.10-
2
-4.3378.
10-
1
320
-1.3748.10-
2
-4.3992.
10-
1
640
-6.9235 .
10-
3
-4.4310 .
10-
1
Table
4.1.
Global error
in
Euler's method for (4.28).
4.4.2 Improving
on
Euler's method: Runge-Kutta methods
If
the
results suggested in
the
previous section
are
correct, Euler's method can
be
used
to
approximate
the
solution
to
an
IVP
to
any desired accuracy by simply
making
tlt
small enough. Although this is
true
(with certain restrictions),
we
might
hope for a more efficient
method-one
that
would
not
require as many time steps
to
achieve a given accuracy.
To improve Euler's method, we choose a numerical integration technique
that
is more accurate
than
the
left-endpoint rule.
The
simplest is
the
midpoint rule:
r
b
(a+b)
la
f(x)
dx
==
(b
-
a)f
-2-
.
If
tlt
= b - a (and
the
integrand f is sufficiently smooth),
then
the
error in
the
midpoint rule
is
O(tlt
3
).
Following
the
reasoning in
the
previous section,
we
expect
that
the
corresponding
method
for integrating
an
IVP
would have
O(tlt
2
)
global
error.
It
is
not
immediately clear how
to
use
the
midpoint rule for
quadrature
to
integrate
an
IVP.
The
obvious equation is
However, after reaching time
ti
in
the
integration,
we
have
an
approximation for
U(ti),
but
none for U(ti +
tlt/2).
To use
the
midpoint rule requires
that
we
first
generate
an
approximation for U(ti +
tlt/2);
the
simplest way
to
do this is with
an
Euler
step:
U
(ti
+
~t)
==
u (ti) +
~t
f (ti,U
(ti)).
Putting
this approximation together with
the
midpoint rule,
and
using
the
approx-
imation
Ui
==
U(ti),
we
obtain
the
improved Euler method:
4.4. Numerical methods
for
initial value problems
105
n
10
20
40
80
160
320
640
Error
in
it
(10)
-2.1629
•
10~
2
-1.2535
-Mr
2
-4.7603
•
1Q-
3
-1.4746
-nr
3
-4.1061
•
10~
4
-1.0835
•
10-
4
-2.7828
•
10~
5
Error
in
«(io)
At
2
-2.1629-1Q-
2
-5.0140
-1Q-
2
-7.6165
-1Q-
2
-9.4376
•
10~
2
-10.512
-1Q-
2
-11.095
-i(r
2
-11.398
-10-
2
Table
4.2.
Global
error
in the
improved
Euler
method
for
(4-28).
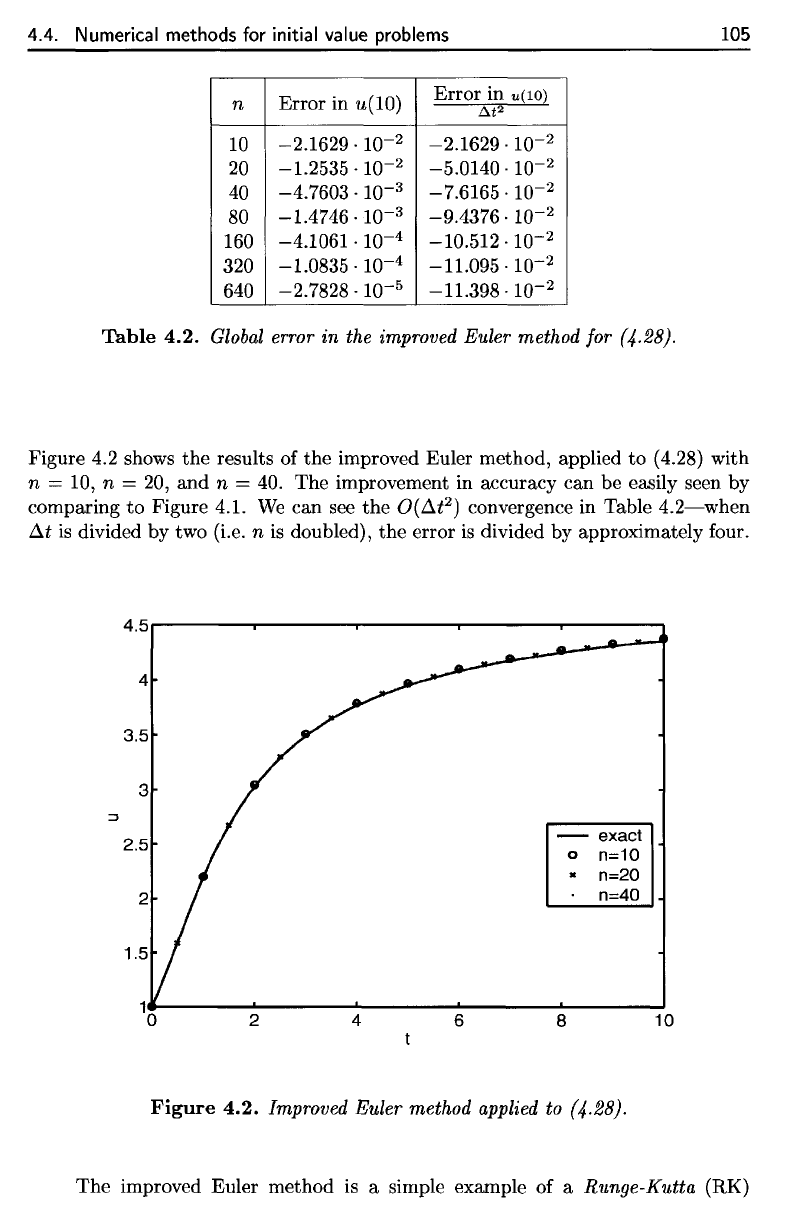
Figure
4.2
shows
the
results
of the
improved Euler method, applied
to
(4.28) with
n — 10, n = 20, and n = 40. The
improvement
in
accuracy
can be
easily seen
by
comparing
to
Figure
4.1.
We can see the
O(At
2
)
convergence
in
Table
4.2—when
At
is
divided
by two
(i.e.
n is
doubled),
the
error
is
divided
by
approximately
four.
Figure
4.2.
Improved Euler method
applied
to
(4-28).
The
improved Euler method
is a
simple example
of a
Runge-Kutta
(RK)
4.4. Numerical methods for initial value problems 105
n
Error
in u(10)
Error
in
u(lO)
lJ.t
2
10
-2.1629.10-
2
-2.1629.10-
2
20
-1.2535
.
10-
2
-5.0140.10-
2
40
-4.7603
.
10-
3
-7.6165.10-
2
80
-1.4746.10-
3
-9.4376.
10-
2
160
-4.1061
. 10-4
-10.512.10-
2
320
-1.0835
. 10-4
-11.095.10-
2
640
-2.7828.10-
5
-11.398.10-
2
Table
4.2.
Global error in the improved Euler method for (4.28).
Figure 4.2 shows
the
results of
the
improved Euler method, applied
to
(4.28) with
n = 10, n = 20,
and
n = 40.
The
improvement in accuracy can
be
easily seen by
comparing
to
Figure 4.1.
We
can see
the
O(~t2)
convergence in Table
4.2-when
~t
is
divided by two
(Le.
n is doubled),
the
error is divided by approximately four.
4.5~------~-------r------~--------r-----~
- exact
o n=10
8
• n=20
n=40
Figure
4.2.
Improved Euler method applied to (4.28).
10
The
improved Euler method is a simple example of a Runge-Kutta (RK)

106
Chapter
4.
Essential
ordinary
differential
equations
method.
An
(explicit)
RK
method takes
the
following
form:
with
certain restrictions
on the
values
of the
parameters
ctj,
PM,
and
7^
(e.g.
a\
+
h
a
m
—
!)•
Although
(4.29)
looks complicated,
it is not
hard
to
understand
the
idea.
A
general
form
for a
quadrature rule
is
where
wi,W2,.--,
w
m
are the
quadrature weights
and
xi,
x%,...,
x
m
G
[a,
b]
axe the
quadrature nodes.
In the
formula
for
Ui+i
in
(4.29),
the
weights
are
Simpson's
rule
has an
error
of
O(A£
5
)
(At = b — a), and the
following
related
method
for
integrating
an
IVP
has
global error
of
O(A£
4
):
and
values
fci,
£2,
• • •
,k
m
are
estimates
of
f(t,u(t))
at ra
nodes
in the
interval
[ti,ti
+
i].
We
will
not use the
general
formula
(4.29),
but the
reader should
ap-
preciate
the
following
point: there
are
many
RK
methods, obtained
by
choosing
various values
for the
parameters
in
(4.29).
This
fact
is
used
in
designing algo-
rithms
that
attempt
to
automatically
control
the
error.
We
discuss
this
further
in
Section
4.4.4
below.
The
most popular
RK
method
is
analogous
to
Simpson's
rule
for
quadrature:
106
Chapter
4.
Essential ordinary differential equations
method. An (explicit) RK method takes
the
following form:
m
ui+1
=
Ui
+
D.t
L
(}:jk
j,
j=l
kl = 1 (ti'
Ui)
,
k2
= 1 (ti +
'Y2D.t,
Ui
+
f321D.tkl)
'
k3
= 1 (ti +
'Y3D.t,
Ui
+
f331D.tk
l
+
f332D.tk2)
,
(4.29)
k
m
= 1
(ti
+'YmD.t,ui +
~
f3mlD.tkl)
,
with certain restrictions on
the
values of the parameters
(}:j,
f3kl,
and
"0
(e.g. (}:l +
... +
(}:m
= 1). Although (4.29) looks complicated,
it
is
not hard
to
understand the
idea. A general form for a quadrature rule
is
where
WI,
W2,
...
,W
m
are the quadrature weights and
Xl,
X2,
...
,X
m
E
[a,
b)
are the
quadrature nodes. In the formula for
Ui+l
in (4.29), the weights are
and
values
kl'
k
2
,
...
, k
m
are estimates of
I(t,
u(t))
at
m nodes in
the
interval
[ti'
ti+1)'
We
will not use the general formula (4.29),
but
the reader should ap-
preciate the following point: there are many RK methods, obtained by choosing
various values for the parameters in (4.29). This fact
is
used in designing algo-
rithms
that
attempt
to
automatically control
the
error.
We
discuss this further in
Section 4.4.4 below.
The most popular RK method
is
analogous
to
Simpson's rule for quadrature:
i
b
I(x)
dx
==
b
~
a
(f(a)
+ 41
(a;
b)
+
f(b))
.
Simpson's rule has an error of
O(D.t
5
)
(D.t
= b - a),
and
the following related
method for integrating an IVP has global error of
O(D.t4):
D.t
Ui+l
=
Ui
+ 6 (k
l
+
2k2
+
2k3
+ k
4
) ,
kl = f (ti'
Ui)
,
(
D.t
D.t)
k2
= 1 ti +
2'
Ui
+ 2 kl ,
(4.30)
(
D.t
D.t)
k3
= 1 ti +
2'
Ui
+ 2
k2
,
k4
= 1 (ti+l,Ui +
D.
tk
3).
4.4. Numerical methods
for
initial
value problems
107
n
10
20
40
80
160
320
640
Error
in
w(10)
1.9941
•
10~
2
1.0614
-Hr
3
6.5959
•
10~
5
4.0108
•
10~
6
2.4500
•
1Q-
7
1.5100
-l(r
8
9.3654
•
10-
10
Error
in
u(io)
At
4
1.9941
•
10~
2
1.6982
•
10~
2
1.6885
•
10~
2
1.6428
•
10~
2
1.6057
-10-
2
1.5833
-10-
2
1.5712
-ID"
2
Table 4.3.
for
(4.28).
Global
error
in the
fourth-order
Runge-Kutta
method
(RK4)
We
call
this
the RK4
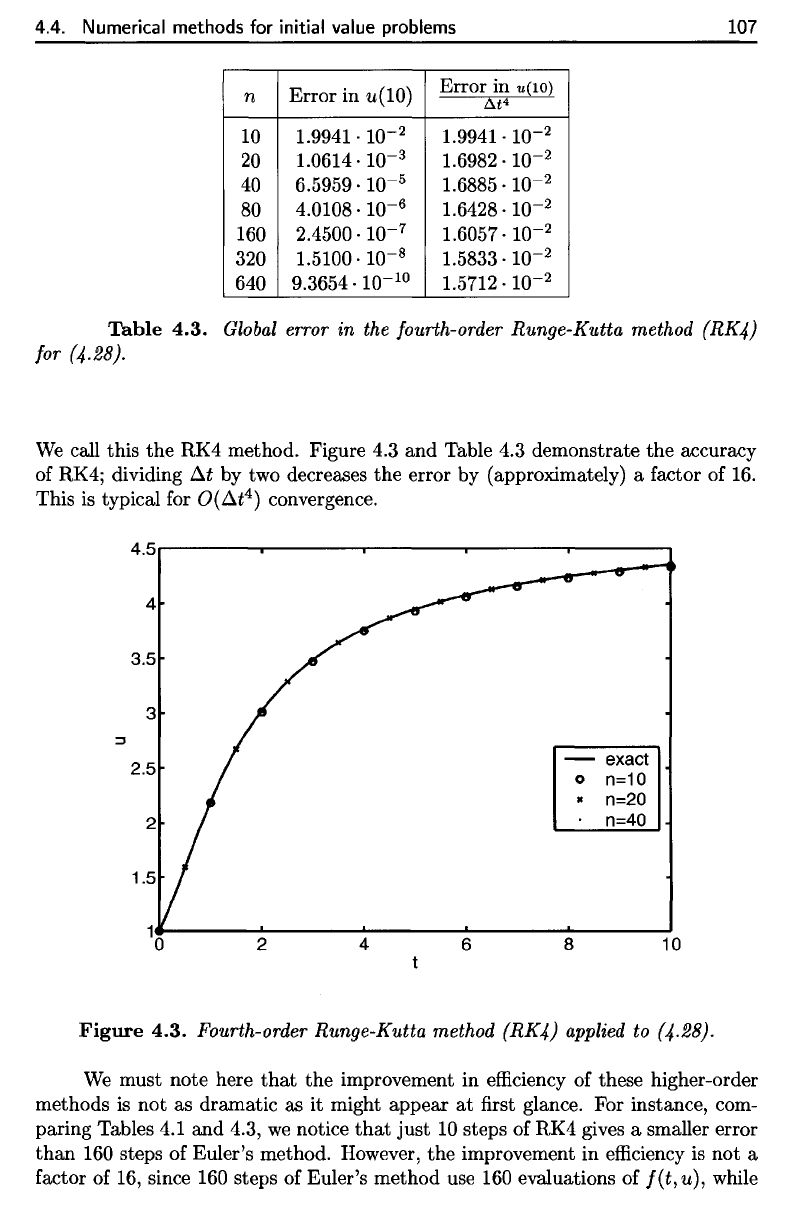
method. Figure
4.3 and
Table
4.3
demonstrate
the
accuracy
of
RK4; dividing
A£
by two
decreases
the
error
by
(approximately)
a
factor
of 16.
This
is
typical
for
O(At
4
)
convergence.
Figure
4.3.
Fourth-order Runge-Kutta method
(RK4)
applied
to
(4-28).
We
must note here
that
the
improvement
in
efficiency
of
these higher-order
methods
is not as
dramatic
as it
might appear
at first
glance.
For
instance,
com-
paring Tables
4.1
and
4.3,
we
notice
that
just
10
steps
of RK4
gives
a
smaller error
than
160
steps
of
Euler's method. However,
the
improvement
in
efficiency
is not a
factor
of 16,
since
160
steps
of
Euler's method
use 160
evaluations
of
f(t,u),
while
4.4. Numerical methods for initial value problems 107
n
Error in
u(10)
Error in
u(10)
.6.t
4
10
1.9941 .
10-
2
1.9941 .
10-
2
20
1.0614.
10-
3
1.6982 .
10-
2
40
6.5959 .
10-
5
1.6885.
10-
2
80
4.0108 .
10-
6
1.6428 .
10-
2
160
2.4500.
10-
7
1.6057.
10-
2
320
1.5100.
10-
8
1.5833 .
10-
2
640
9.3654.
10-
10
1.5712 .
10-
2
Table
4.3.
Global
error in the fourth-order Runge-Kutta method (RK4)
for (4.28).
We
call this
the
RK4 method. Figure 4.3 and Table 4.3 demonstrate the accuracy
of RK4; dividing
D..t
by two decreases
the
error by (approximately) a factor of
16.
This
is
typical for
O(D..t4)
convergence.
4.5r-------~-------r------~--------r_----__,
- exact
o n=10
..
n=20
n=40
8 10
Figure
4.3.
Fourth-order Runge-Kutta method (RK4) applied to (4.28).
We
must note here
that
the improvement in efficiency of these higher-order
methods
is
not as dramatic as
it
might appear
at
first glance. For instance, com-
paring Tables 4.1 and 4.3,
we
notice
that
just
10
steps of RK4 gives a smaller error
than
160 steps of Euler's method. However, the improvement in efficiency
is
not a
factor of
16,
since 160 steps of Euler's method use
160
evaluations of
f(t,
u), while
