Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


68
Chapter
3.
Essential
linear
algebra
Find
the
relationship
y =
mx
+ c
that
best
fits
these
data.
Plot
the
data
and
the
best
fit
line.
8.
Consider
the
following
data:
X
1.0000
1.2500
1.4000
1.5000
1.9000
2.1000
2.2500
2.6000
2.9000
y
1.2475
1.6366
1.9823
2.2243
3.4766
4.2301
4.8478
6.5129
8.2331
Find
the
relationship
y =
c^x
2
+C\X
+
CQ
that
best
fits
these
data.
If
possible,
plot
the
data
and the
best
fit
parabola.
9.
Using
the
orthonormal basis
{^1,^2,^3}
for
P%
given
in
Example 3.39,
find
the
quadratic polynomial
p(x]
that
best approximates g(x)
— sin
(TTX),
in the
mean-square sense, over
the
interval
[0,1].
Produce
a
graph
of g and the
quadratic
approximation.
10. (a)
Verify
that
(<7i,
#2)
#3},
defined
in
Example 3.39,
is an
orthonormal basis
for
P
2
on the
interval
[0,1].
(b)
Using this orthonormal basis,
find the
best approximation
to
f(x)
=
e
x
(on
the
interval
[0,1])
in the
mean-square sense,
and
verify
that
the
same
result
is
obtained
as in
Example 3.38.
3.5
Eigenvalues
and
eigenvectors
of a
symmetric
matrix
The
eigenvectors
of a
matrix operator
are
special vectors
for
which
the
action
of
the
matrix
is
particularly simple.
In
this section,
we
discuss
the
properties
of
eigenvalues
and
eigenvectors
of
symmetric matrices. Understanding this topic
will
set the
stage
for the
Fourier series method
for
solving
differential
equations,
which
takes advantage
of the
simple action
of a
differential
operator
on its
eigenfunctions.
Definition
3.40.
Let A 6
R
nxn
.
We say
that
the
scalar
A is an
eigenvalue
of
A
if
there exists
a
nonzero
vector
x
such that
As we
discuss
below,
the
scalar
A may be
complex
even
if A has
only
real
entries;
if
A is
complex,
then
x
must
have
complex
entries.
68
Chapter
3.
Essential
linear
algebra
Find the relationship y =
mx
+ C
that
best fits these data.
Plot
the
data
and
the best fit line.
8.
Consider the following data:
x
Y
1.0000 1.2475
1.2500 1.6366
1.4000 1.9823
1.5000 2.2243
1.9000
3.4766
2.1000
4.2301
2.2500 4.8478
2.6000 6.5129
2.9000 8.2331
Find
the
relationship y =
C2X
2
+
C1X
+
Co
that
best fits these data.
If
possible,
plot the
data
and the best fit parabola.
9.
Using the orthonormal basis {Ql,Q2,q3} for P2 given in Example 3.39, find
the quadratic polynomial
p(x)
that
best approximates g(x) = sin (nx), in the
mean-square sense, over the interval [0,1]. Produce a graph of
9 and the
quadratic approximation.
10.
(a) Verify
that
{Ql,
Q2,
Q3},
defined in Example 3.39,
is
an orthonormal basis
for
P
2
on the interval [0,1].
(b) Using this orthonormal basis, find
the
best approximation to
f(x)
=
eX
(on
the
interval [0,1]) in the mean-square sense,
and
verify
that
the same
result
is
obtained
as
in Example 3.38.
3.5 Eigenvalues and eigenvectors of a symmetric
matrix
The eigenvectors of a matrix operator are special vectors for which the action of
the
matrix
is
particularly simple. In this section,
we
discuss
the
properties of
eigenvalues and eigenvectors of symmetric matrices. Understanding this topic will
set the stage for the Fourier series method for solving differential equations, which
takes advantage of the simple action of a
differential operator on its eigenfunctions.
Definition
3.40.
Let A E Rnxn. We say that the scalar A is an eigenvalue
of
A
if
there exists a nonzero vector x such that
Ax
=
AX.
As
we discuss
below,
the scalar A
may
be
complex even
if
A has only real entries;
if
A is complex, then x
must
have complex entries.

3.5. Eigenvalues
and
eigenvectors
of a
symmetric matrix
69
As
we are
about
to
demonstrate, eigenvalues
are
naturally expressed
as the
roots
of a
polynomial, with
the
coefficients
of the
polynomial computed
from
the
entries
in the
matrix.
A
polynomial with real
coefficients
can
have complex roots.
For
this reason,
it is
natural
to
allow complex eigenvalues
and
eigenvectors
in the
above definition. However,
we
will show below
that
a
symmetric
matrix
can
have
only
real eigenvalues, which
will
simplify
matters. Moreover,
the
eigenvalues
and
eigenvectors
of a
symmetric matrix have other
useful
properties, which
we
also
explore below.
The
following
calculation
is
essential
for
understanding eigenvalues
and
eigen-
vectors:
Then
12
We
assume
that
the
reader
is
familiar with
the
elementary properties
of
determinants (such
as
the
computation
of
determinants
of
small
matrices).
The
most important
of
these
is
that
a
matrix
is
singular
if and
only
if its
determinant
is
zero.
Any
introductory
text
on
linear algebra, such
as
[34],
can be
consulted
for
details.
where
det(B)
is the
determinant
12
of the
square matrix
B.
In
principle, then,
we
can find the
eigenvalues
of A by
solving
the
equation
det (AI
—
A) = 0.
It is not
hard
to
show
that
PA
(A)
= det (AI
—
A) is a
polynomial
of
degree
n
(the characteristic polynomial
of
A),
and so A has n
eigenvalues (counted according
to
multiplicity
as
roots
of PA
(A)).
Any or all of the
eigenvalues
can be
complex,
even
if A has
real entries, since
a
polynomial with real
coefficients
can
have complex
roots.
This
last
condition
is
possible
if and
only
if AI
—
A is a
singular matrix;
that
is, if
and
only
if
Therefore,
the
eigenvalues
are
3.5. Eigenvalues and eigenvectors
of
a symmetric matrix
69
As
we
are
about
to
demonstrate, eigenvalues are naturally expressed as
the
roots of a polynomial, with
the
coefficients of the polynomial computed from
the
entries in the matrix. A polynomial with real coefficients can have complex roots.
For this reason, it
is
natural
to
allow complex eigenvalues
and
eigenvectors in
the
above definition. However,
we
will show below
that
a symmetric
matrix
can have
only real eigenvalues, which will simplify matters. Moreover, the eigenvalues
and
eigenvectors of a symmetric matrix have other useful properties, which
we
also
explore below.
The
following calculation is essential for understanding eigenvalues
and
eigen-
vectors:
Ax=
.>.x,
x:f:.O
{:}
.>.x
-
Ax
=
0,
x
:f:.
0
{:}
(.>.1
-
A)x
=
0,
x:f:.
o.
This last condition is possible if
and
only
if
'>'1
- A
is
a singular matrix;
that
is, if
and
only if
det
(.>.1
- A) = 0,
where
det(B)
is
the
determinant
12
of
the
square
matrix
B.
In principle, then,
we
can find
the
eigenvalues of A by solving
the
equation det
(.>.1
- A) =
O.
It
is not
hard
to
show
that
PA('>')
= det
(.>.1
- A)
is
a polynomial of degree n
(the characteristic polynomial of
A),
and
so A has n eigenvalues (counted according
to
multiplicity as roots of
PA('>')).
Any or all of
the
eigenvalues can be complex,
even if A has real entries, since a polynomial with real coefficients can have complex
roots.
Example
3.41.
Let
Then
PA('>')
= det
(.>.1
- A)
Therefore, the eigenvalues
are
-1
1
'>'-1
-
-1
.>.
- 2
=
(.>.
-
1)('>'
-
2)
-1
=.>.2
_
3'>'
+
1.
3±
v'5
2
12We assume
that
the
reader
is familiar
with
the
elementary properties of
determinants
(such as
the
computation
of
determinants
of small matrices).
The
most
important
of these is
that
a
matrix
is singular if
and
only if
its
determinant
is zero. Any
introductory
text
on
linear algebra, such as
[34],
can
be
consulted for details.
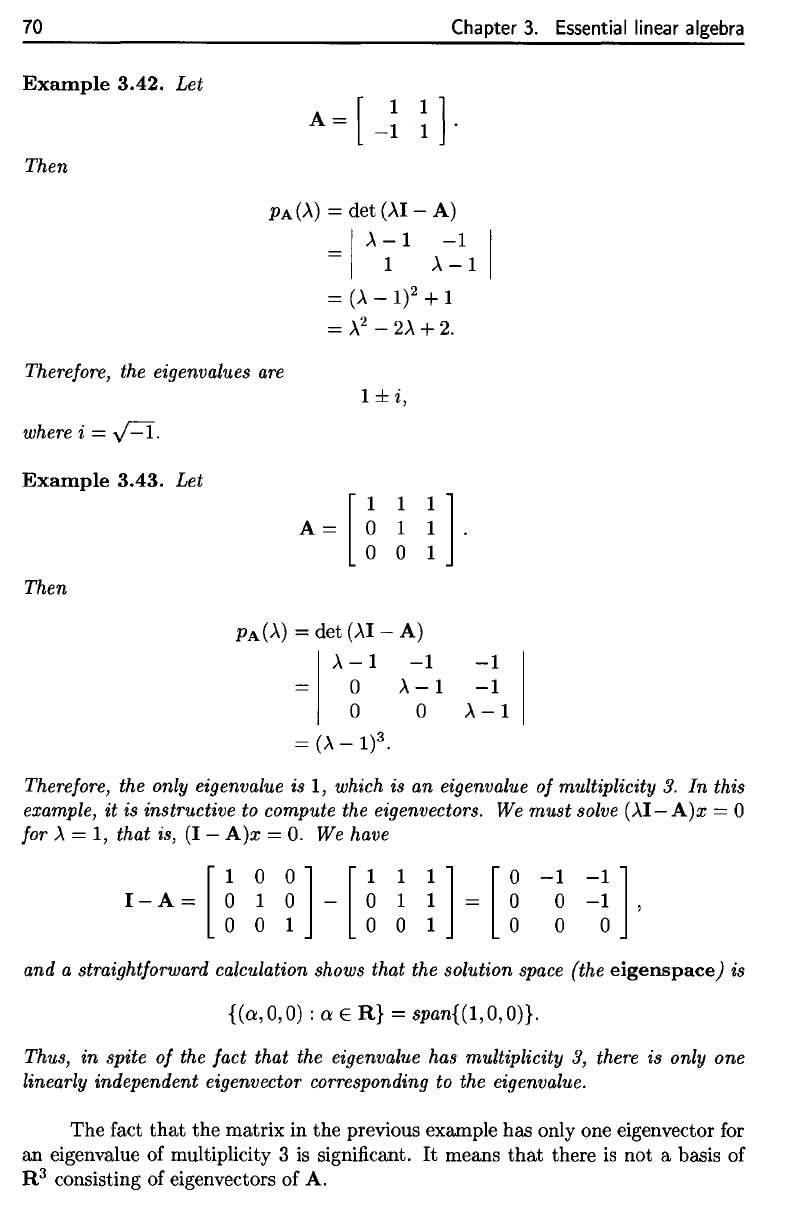
70
Chapter
3.
Essential linear algebra
Example
3.42.
Let
Then
Therefore,
the
eigenvalues
are
where
i =
^f—^..
Example
3.43.
Let
Then
Therefore,
the
only
eigenvalue
is
I,
which
is an
eigenvalue
of
multiplicity
3. In
this
example,
it is
instructive
to
compute
the
eigenvectors.
We
must
solve
(XI
—
A.)x
= 0
for
A = 1,
that
is, (I
—
A)x = 0. We
have
Thus,
in
spite
of the
fact that
the
eigenvalue
has
multiplicity
3,
there
is
only
one
linearly
independent eigenvector corresponding
to the
eigenvalue.
The
fact
that
the
matrix
in the
previous example
has
only
one
eigenvector
for
an
eigenvalue
of
multiplicity
3 is
significant.
It
means
that
there
is not a
basis
of
R
3
consisting
of
eigenvectors
of A.
and
a
straightforward
calculation shows that
the
solution
space
(the
eigenspace)
is
70
Example
3.42.
Let
Then
Chapter
3.
Essential linear algebra
PA
(A)
= det
(AI
-
A)
=1
A-I
-1
1
A-I
=
(A
- 1)2 + 1
=
A2
-
2A
+ 2.
Therefore, the eigenvalues
are
wherei=A·
Example
3.43.
Let
Then
1 ± i,
PA(A)
= det
(AI
-
A)
-1
A-I
o
-1
-1
A-I
Therefore, the only eigenvalue is 1, which is an eigenvalue
of
multiplicity
3.
In
this
example,
it
is instructive to compute the eigenvectors. We
must
solve
(AI
-
A)x
= 0
for A = 1, that
is,
(I -
A)x
=
O.
We have
[
1 0 0
1
[1
III
[0
-1 -1
1
I - A = 0 1 0 - 0 1 1 = 0 0
-1
,
001 001
000
and a straightforward calculation shows that the solution
space
(the
eigenspace)
is
{(a,O,O) : a E R} = span{(I,O,O)}.
Thus, in spite
of
the fact that the eigenvalue has multiplicity 3, there is only one
linearly independent eigenvector corresponding to the eigenvalue.
The
fact
that
the
matrix
in
the
previous example has only one eigenvector for
an
eigenvalue of multiplicity 3
is
significant.
It
means
that
there
is
not a basis of
R3
consisting of eigenvectors of
A.

3.5. Eigenvalues
and
eigenvectors
of a
symmetric
matrix
71
3.5.1
The
transpose
of a
matrix
and the dot
product
The
theory
of
eigenvalues
and
eigenvectors
is
greatly
simplified
when
a
matrix
A
e
R
nxn
is
symmetric,
that
is,
when
A
T
= A. In
order
to
appreciate this,
we
need
to
understand
the
relationship
of the
transpose
of a
matrix
to the
Euclidean inner
product
(or dot
product).
We
consider
a
linear operator
defined
by A
e
R
mxn
,
and
perform
the
following
calculation:
(The above manipulations
are
just applications
of the
elementary properties
of
arithmetic—basically
that
numbers
can be
added
in any
order,
and
multiplication
distributes over addition.) Thus
the
transpose
A
T
of A €
R
mxn
satisfies
the
following
fundamental property:
For
a
symmetric matrix
A
e
R
nxn
,
this
simplifies
to
When
we
allow
for
complex scalars
and
vectors with complex entries,
we
must
modify
the dot
product.
If x, y 6
C
n
,
then
we
define
The
second vector
in a dot
product must thus
be
conjugated; this
is
necessary
so
that
x-x
will
be
real, allowing
the
norm
to be
defined.
We
will
use the
same notation
for
the dot
product whether
the
vectors
are in
R
n
or
C
n
.
The
complex
dot
product
has the
following
properties, which
form
the
definition
of an
inner product
on a
complex
vector space:
1.
x • x
>
0 for all x
6
C
n
,
and x • x
=
0 if and
only
if x = 0.
2.
x • y = y •
x
for all x, y 6
C
n
.
3.5. Eigenvalues and eigenvectors
of
a symmetric matrix
71
3.5.1 The
transpose
of a matrix
and
the dot product
The theory of eigenvalues and eigenvectors
is
greatly simplified when a matrix A E
Rnxn
is symmetric,
that
is, when
AT
= A.
In
order
to
appreciate this,
we
need
to understand the relationship
of
the
transpose of a matrix
to
the
Euclidean inner
product (or dot product).
We
consider a linear operator defined by A E R m x
n,
and perform the following
calculation:
n m
=
LLAijViUj
j=l
i=l
n
j=l
(The above manipulations are
just
applications of the elementary properties of
arithmetic-basically
that
numbers can be added in any order, and multiplication
distributes over addition.) Thus the transpose
AT
of A E
Rmxn
satisfies
the
following fundamental property:
(3.25)
For a symmetric matrix A E R
nxn
, this simplifies to
(Au)
. v =
u·
(Av) for all
u,
vERn.
When
we
allow for complex scalars
and
vectors with complex entries,
we
must
modify the dot product.
If
x,
y E
en,
then
we
define
n
x·y
=
LXiYi.
i=l
The second vector in a dot product must thus be conjugated; this
is
necessary so
that
X·X
will be real, allowing
the
norm
to
be defined.
We
will use the same notation
for
the
dot product whether the vectors are in R
n
or
en.
The
complex dot product
has the following properties, which form the definition of
an
inner product on a
complex vector space:
1.
X·
x
~
0 for all x E
en,
and x . x = 0 if and only if x =
o.
2.
X·
Y = Y . x for all
x,
y E
en.

72
Chapter
3.
Essential
linear
algebra
3. (ax +
/3y)
• z = ax • z +
0y
• z for all
x,y,
z 6
C
n
,
a, ft £ C.
Together with
the
second property, this implies
that
for
all
x,y,z
£
C
n
,
a,/3
£ C.
Complex
vector spaces
and
inner products
are
discussed
in
more
detail
in
Section
9.1.
3.5.2 Special properties
of
symmetric matrices
We
can now
derive
the
special properties
of the
eigenvalues
and
eigenvectors
of a
symmetric
matrix.
Theorem
3.44.
//A
e
R
nxn
is
symmetric, then
every
eigenvalue
of
A is
real.
Moreover,
each
eigenvalue
corresponds
to a
real
eigenvector.
Proof. Suppose
Ax = Ax, x
/
0,
where
for the
moment
we do not
exclude
the
possibility
that
A and x
might
be
complex. Then
and
But
(Ax)
• x = x •
(Ax) when
A is
symmetric,
so
Since
x • x
/
0,
this yields
which implies
that
A is
real.
Let
x =
u
+
iv,
where
u, v £
R
n
.
Then
Since
x
7^
0, we
must have either
u
/
0 or v
^
0 (or
both),
so one of u, v (or
both)
must
be a
real eigenvector
of A
corresponding
to A.
Prom this point
on, we
will
only discuss eigenvalues
and
eigenvectors
for
real
symmetric
matrices.
According
to the
last
theorem,
then,
we
will
not
need
to use
complex numbers
or
vectors.
Theorem
3.45.
Let A £
R
nxn
be
symmetric,
and let
xi,
x
2
be
eigenvectors
of
A
corresponding
to
distinct eigenvalues
\i,
\2-
Then
xi
and
X2
are
orthogonal.
72 Chapter
3.
Essential linear algebra
3.
(ax
+
f3y)
. z =
ax·
z +
f3y
. z for all
x,
y,
z E
en,
a,
f3
E
e.
Together with
the
second property, this implies
that
z .
(ax
+
f3y)
=
az
. x +
f3z
. y
for all
x,y,z
E
en,
a,f3 E
e.
Complex vector spaces
and
inner products are discussed in more detail in Section
9.1.
3.5.2 Special properties
of
symmetric matrices
We
can now derive
the
special properties of
the
eigenvalues
and
eigenvectors of a
symmetric matrix.
Theorem
3.44.
If
A E Rnxn is symmetric, then every eigenvalue
of
A is real.
Moreover, each eigenvalue corresponds to a real eigenvector.
Proof.
Suppose
Ax
=
AX,
x
=P
0, where for
the
moment
we
do not exclude
the
possibility
that
A and x might be complex.
Then
(Ax)
. x =
(AX)
. x =
A(X
. x)
and
x·
(Ax)
= x .
(AX)
= X(x . x).
But
(Ax)
. x = x .
(Ax)
when A is symmetric, so
A(X
. x) = X(x . x).
Since x . x
i:-
0, this yields
A =
A,
which implies
that
A is real.
Let x
= U +
iv,
where
u,
vERn.
Then
Ax
=
AX
<=>
A(u
+
iv)
=
A(U
+
iv)
<=>
Au
+
iAv
=
AU
+
iAV
<=>
{
Au
=
AU,
Av
=
AV.
Since x
i:-
0,
we
must have either U
=P
0 or v
f:-
0 (or both), so one of
u,
v (or both)
must
be
a real eigenvector of A corresponding
to
A.
0
From this point on,
we
will only discuss eigenvalues
and
eigenvectors for real
symmetric matrices. According
to
the
last
theorem, then,
we
will
not
need
to
use
complex numbers or vectors.
Theorem
3.45.
Let
A E Rnxn
be
symmetric, and let Xl,
X2
be
eigenvectors
of
A
corresponding to distinct eigenvalues
AI,
A2.
Then
Xl
and
X2
are
orthogonal.

3.5. Eigenvalues
and
eigenvectors
of a
symmetric
matrix
73
Example 3.46.
Consider
so
the
eigenvalues
of
A are
0,0,1.
Another
straightforward
calculation shows that
there
are two
linearly independent eigenvectors corresponding
to X —
0,
namely,
We
can
verify
by
observation that
the
eigenvectors
for X = 0 are
orthogonal
to the
eigenvector
for A =
1.
Here
is
another
special property
of
symmetric matrices.
Example
3.43
shows
that
this
result
is not
true
for
nonsymmetric matrices.
Theorem 3.47.
Let A 6
R
nxn
be
symmetric,
and
suppose
A has an
eigenvalue
IJL
of
(algebraic)
multiplicity
k
(meaning that
fj,
is a
root
of
multiplicity
k of the
characteristic polynomial
of
A).
Then
A has k
linearly independent eigenvectors
corresponding
to
[L.
Proof.
We
have
But
and
Therefore
and
since
AI
^
A
2
,
this
implies
that
(xi,x
2
)
= 0.
A
straightforward
calculation shows that
and
a
single (independent) eigenvector
for A =
1,
3.5. Eigenvalues
and
eigenvectors
of
a symmetric matrix
Proof.
We
have
But
and
Therefore
Al(XI
.
X2)
=
A2(Xl
.
X2),
and since
Al
i-
A2,
this implies
that
(Xl,X2) =
0.
D
Example
3.46.
Consider
[
1/3
1/3
A =
1/3 1/3
1/3 1/3
A straightforward calculation shows that
1/3]
1/3
.
1/3
73
so the eigenvalues
of
A are 0,0, 1.
Another
straightforward calculation shows that
there are two linearly independent eigenvectors corresponding to ,\ = 0, namely,
and a single (independent) eigenvector for ,\
= 1,
We can verify
by
observation that the eigenvectors for A = °
are
orthogonal to the
eigenvector for
A =
1.
Here
is
another special property of symmetric matrices. Example 3.43 shows
that
this result
is
not true for nonsymmetric matrices.
Theorem
3.47.
Let
A E R
nxn
be
symmetric, and suppose A has an eigenvalue
J1-
of
(algebraic) multiplicity k (meaning that
J1-
is a root
of
multiplicity k
of
the
characteristic polynomial
of
A). Then A has k linearly independent eigenvectors
corresponding to
J1-.
.

74
Chapter
3.
Essential linear algebra
The
proof
of
this theorem
is
rather
involved
and
does
not
generalize
to
differ-
ential operators
(as do the
proofs
given
above).
We
therefore relegate
it to
Appendix
A.
If
n
is an
eigenvalue
of
multiplicity
k,
as in the
previous theorem,
then
we can
choose
the k
linearly independent eigenvectors corresponding
to
//
to be
orthonor-
mal.
13
We
thus
obtain
the
following
corollary.
Corollary
3.48. (The
spectral
theorem
for
symmetric
matrices)
Let A
G
R
nxn
be
symmetric. Then
there
is an
orthonormal
basis
{ui,u
2
,...
,u
n
)
of
R
n
consisting
of
eigenvectors
of
A.
3.5.3
The
spectral method
for
solving
Ax = b
When
A
e
R
nxn
is
symmetric
and the
eigenvalues
and
eigenvectors
of A are
known,
there
is a
simple
method
14
for
solving
Ax = b.
Let
A be
symmetric with eigenvalues
AI
,
\
2
,...,
A
n
and
orthonormal eigen-
vectors
ui,
U2,...,
u
n
.
For any b
e
R
n
,
we can
write
that
is,
13
It is
always possible
to
replace
any
linearly independent
set
with
an
orthonormal
set
spanning
the
same subspace.
The
technique
for
doing
this
is
called
the
Gram-Schmidt procedure;
it is
explained
in
elementary linear algebra
texts
such
as
[34].
14
This
method
is not
normally taught
in
elementary linear algebra courses
or
books, because
it
is
more
difficult
to find the
eigenvalues
and
eigenvectors
of A
than
to
just solve
Ax
=
b by
other
means.
Thus
we
obtain
the
solution
Since
b can
have only
one
expansion
in
terms
of the
basis
{ui,...
,u
n
},
we
must
have
We
can
also write
(Of
course,
o,i
=
Uj
• x,
but,
as we are
thinking
of x as the
unknown,
we
cannot
compute
o>i
from
this
formula.)
We
then have
74
Chapter
3. Essential linear algebra
The proof of this theorem
is
rather involved and does not generalize to differ-
ential operators (as do the proofs given above).
We
therefore relegate it to Appendix
A.
If
/L
is
an eigenvalue of multiplicity k, as in the previous theorem, then
we
can
choose the
k linearly independent eigenvectors corresponding to
/L
to
be orthonor-
mal.
13
We
thus obtain the following corollary.
Corollary
3.48.
(The
spectral
theorem
for
symmetric
matrices)
Let A E
Rnxn
be
symmetric. Then there is an orthonormal basis
{Ul'
U2,
...
,un}
of
Rn
consisting
of
eigenvectors
of
A.
3.5.3
The
spectral method for solving
Ax
= b
When A E
Rnxn
is
symmetric and
the
eigenvalues and eigenvectors of A are known,
there
is
a simple method
14
for solving
Ax
=
b.
Let A be symmetric with eigenvalues
AI,
A2,
...
,An
and orthonormal eigen-
vectors
Ul,
U2,
...
,Un'
For any b
ERn,
we
can write
We
can also write
(Of course,
ai
=
Ui
.
x,
but, as
we
are thinking of x as the unknown,
we
cannot
compute
ai
from this formula.)
We
then have
Ax
=
b::::}
A
(alul
+ ... +
anu
n
) = (Ul .
b)Ul
+ ... +
(un'
b)u
n
::::}
alAul
+ ... +
anAu
n
= (Ul . b)UI + ... +
(un'
b)u
n
::::}
alAlUl
+ ... + anAnUn = (Ul .
b)Ul
+ ... +
(un'
b)u
n
.
Since b can have only one expansion in terms of
the
basis {Ul,
...
,
un},
we
must
have
aiAi
=
(Ui'
b),
i =
1,2,
..
.
,n,
that
is,
Thus
we
obtain the solution
(3.26)
13It is always possible
to
replace
any
linearly independent
set
with
an
orthonormal
set
spanning
the
same
subspace.
The
technique for doing
this
is called
the
Gram-Schmidt
procedure; it is
explained in elementary linear algebra
texts
such as
[34].
14This
method
is
not
normally
taught
in elementary linear algebra courses
or
books, because
it
is more difficult
to
find
the
eigenvalues
and
eigenvectors of A
than
to
just
solve
Ax
= b
by
other
means.

3.5.
Eigenvalues
and
eigenvectors
of a
symmetric matrix
75
We
see
that
all of the
eigenvalues
of A
must
be
nonzero
in
order
to
apply this
method, which
is
only sensible:
if 0 is an
eigenvalue
of A,
then
A is
singular
and
Ax
=
b
either
has no
solution
or has
infinitely many solutions.
If
we
already have
the
eigenvalues
and
eigenvectors
of A,
then this method
for
solving
Ax
=
b is
simpler
and
less expensive
than
the
usual method
of
Gaussian
elimination.
Example
3.49.
Let
A
direct
calculation shows that
the
eigenvalues
of
A are
and
the
corresponding
(orthonormal)
eigenvectors
are
Compute,
by
hand,
the
eigenvalues
and
eigenvectors
of A, and use
them
to
solve
Ax
—
b for x
(use
the
"spectral
method").
2.
Repeat Exercise
1 for
(According
to
Theorem 3.45,
the
eigenvectors
are
automatically orthogonal
in
this
case;
however,
we had to
ensure that
each
eigenvector
was
normalized.)
The
solution
to
Ax = b is
Exercises
1. Let
3.5. Eigenvalues and eigenvectors
of
a symmetric matrix
75
We
see
that
all of the eigenvalues of A must be nonzero in order
to
apply this
method, which
is
only sensible: if 0
is
an eigenvalue of
A,
then A
is
singular and
Ax
= b either has no solution or has infinitely many solutions.
If
we
already have the eigenvalues
and
eigenvectors of
A,
then this method for
solving
Ax
= b
is
simpler and less expensive
than
the usual method of Gaussian
elimination.
Example
3.49.
Let
[
11
-4
-1
1 [ 1 1
A =
-4
14
-4
,b
= 2
-1
-4
11
1
A direct calculation shows that the eigenvalues
of
A
are
A1
=
6,
A2
= 12,
A3
= 18,
and the corresponding (orthonormal) eigenvectors
are
(According to Theorem 3.45, the eigenvectors
are
automatically orthogonal in this
case; however,
we
had to ensure that each eigenvector was normalized.) The solution
to
Ax
= b is
Exercises
1.
Let
[
164
-48]
[
116
]
A =
-48
136
,b
= 88 .
Compute, by hand, the eigenvalues and eigenvectors of
A,
and
use them
to
solve
Ax
= b for x (use the "spectral method").
2.
Repeat Exercise 1 for
A=
3
-1
-1
] [
11
]
3
,b
=
-9
.

76
Chapter
3.
Essential linear algebra
3.
Repeat Exercise
1 for
4.
Repeat Exercise
1 for
where
h =
l/(n
+
1).
For
example, with
n = 5,
(b)
What
is the
relationship between
the
frequency
j and the
magnitude
of
A,-?
Show
that
s(
J
)
is an
eigenvector
of L, and find the
corresponding eigen-
value
Xj.
(Hint: Compute
Ls(
J
)
and
apply
the
addition formula
for the
sine
function.)
(a)
For
each
j =
1,2,...,
n,
define
the
discrete sine wave
s^
of
frequency
j
by
7.
Let L be the n x n
matrix
defined
by the
condition
that
5.
Let A €
R
nxn
be
symmetric,
and
suppose
the
eigenvalues
and
(orthonormal)
eigenvectors
of A are
already known.
How
many arithmetic operations
are
required
to
solve
Ax = b
using
the
spectral method?
6.
A
symmetric matrix
A
e
R
nxn
is
called positive
definite
if
Use
the
spectral theorem
to
show
that
A is
positive definite
if and
only
if all
of
the
eigenvalues
of A are
positive.
76
Chapter
3.
Essential linear algebra
3.
Repeat
Exercise 1 for
4.
Repeat
Exercise 1 for
[
7
-2
1]
[
6]
A =
-2
10
-2
,b
=
12
.
1
-2
7
18
5. Let A E R
nxn
be symmetric,
and
suppose
the
eigenvalues
and
(orthonormal)
eigenvectors of A
are
already known. How
many
arithmetic operations are
required
to
solve
Ax
= b using
the
spectral method?
6. A symmetric
matrix
A E
Rnxn
is called positive definite if
x
=I
0
~
(Ax)
. x >
O.
Use
the
spectral theorem
to
show
that
A is positive definite if
and
only if all
of
the
eigenvalues of A are positive.
7. Let L
be
the
n x n
matrix
defined by
the
condition
that
p,
i =
j,
{
2
Lij
=
-b,
0,
li-jl=1,
otherwise,
where h =
1j(n
+ 1). For example, with n = 5,
[
72
-36
° 0
-36
72
-36
0
L = 0
-36
72
-36
o 0
-36
72
o 0 0
-36
01
o
o .
-36
72
(a) For each j =
1,2,
...
,n,
define
the
discrete sine wave s(j) of frequency j
by
s~)
= sin (jk7rh).
Show
that
s(j) is
an
eigenvector
of
L,
and
find
the
corresponding eigen-
value Aj. (Hint: Compute Ls(j)
and
apply
the
addition formula for
the
sine function.)
(b)
What
is
the
relationship between
the
frequency j
and
the
magnitude
of
Aj?

3.6. Preview
of
methods
for
solving ODEs
and
PDEs
77
(c)
The
discrete sine waves
are
orthogonal (since they
are the
eigenvectors
of
a
symmetric matrix corresponding
to
distinct eigenvalues)
and
thus
form
an
orthogonal basis
for
R
n
.
Moreover,
it can be
shown
that
every
s(^
has the
same norm:
Therefore,
I
V2hs^
l
\
^/2hs^
2
\
...,
\/2hs^
>
is an
orthonormal
basis
for
R
n
.
We
will
call
a
vector
x
e
R
n
smooth
or
rough depending
on
whether
its
components
in the
discrete sine wave basis
are
heavily weighted toward
the low or
high frequencies, respectively. Show
that
the
solution
x of
Lx
= b is
smoother
than
b.
3.6
Preview
of
methods
for
solving ODEs
and
PDEs
The
close formal relation between
the
concepts
of
linear
differential
equation
and
linear algebraic system suggests
that
ideas about linear operators might play
a
role
in
solving
the
former,
as is the
case
for the
latter.
In
order
to
make this parallel
explicit,
we
will
apply
the
machinery
of
linear algebra
in the
context
of
differential
equations: view solutions
as
vectors
in a
vector space,
identify
the
linear operators
which
define
linear
differential
equations,
and
understand
how
facts such
as the
Fredholm alternative appear
in the
context
of
differential
equations.
In the
chapters
to
follow
we
will
accomplish
all of
this.
In the
process,
we
will
develop
three general classes
of
methods
for
solving linear ODEs
and
PDEs, each
one
closely analogous
to a
method
for
solving linear algebraic systems:
1.
The
method
of
Fourier
series:
Differential
operators, like
d?/dx
2
,
can
have
eigenvalues
and
eigenfunctions;
for
example
The
method
of
Fourier series
is a
spectral method, using
the
eigenfunctions
of
the
differential operator.
2.
The
method
of
Green's
functions:
A
Green's function
for a
differential
equation
is the
solution
to a
special
form
of the
equation
(just
as
A"
1
is the
solution
to AB = /)
that
allows
one to
immediately write down
the
solution
to the
equation (just
as we
could write down
x =
A
-1
b).
3.
The
method
of finite
elements:
This
is a
direct numerical method
that
can be
used when
(1) or (2)
fails
(or is
intractable).
It can be
compared
with
Gaussian elimination,
the
standard
direct numerical method
for
solving
Ax
=
b.
Like Gaussian elimination,
finite
element methods
do not
produce
a
formula
for the
solution; however, again like Gaussian elimination, they
are
broadly applicable.
3.6. Preview
of
methods for solving
ODEs
and
PDEs
77
(c)
The
discrete sine waves are orthogonal (since they are the eigenvectors
of a symmetric matrix corresponding to distinct eigenvalues)
and
thus
form
an
orthogonal basis for Rn. Moreover,
it
can
be
shown
that
every
s(j)
has the same norm:
II
(j)
11-
1 . - 1 2
s - V2h' J - , ,
..
. ,n.
Therefore, {
V2hs(1)
,
V2hS(2),
... ,V2hs(n)} is
an
orthonormal basis for
Rn.
We
will call a vector x E Rn smooth or rough depending on whether
its components in the discrete sine wave basis are heavily weighted toward
the low or high frequencies, respectively. Show
that
the solution x of
Lx
= b
is
smoother
than
b.
3.6 Preview of methods
for
solving
ODEs
and
PDEs
The close formal relation between the concepts of linear differential equation and
linear algebraic system suggests
that
ideas about linear operators might
playa
role
in solving the former, as
is
the case for the latter. In order
to
make this parallel
explicit,
we
will apply the machinery of linear algebra in the context of differential
equations: view solutions as vectors in a vector space, identify
the
linear operators
which define linear differential equations, and understand how facts such as the
Fredholm alternative appear in
the
context of differential equations.
In
the
chapters
to
follow
we
will accomplish all of this.
In
the process,
we
will
develop three general classes of methods for solving linear ODEs and PDEs, each
one closely analogous
to
a method for solving linear algebraic systems:
1.
The
method
of
Fourier
series:
Differential operators, like d
2
/
dx
2
,
can have
eigenvalues and eigenfunctions; for example
;:2
[sin(wx)] =
_w
2
sin(wx).
The
method of Fourier series
is
a spectral method, using the eigenfunctions
of
the
differential operator.
2.
The
method
of
Green's
functions:
A Green's function for a differential
equation
is
the solution
to
a special form of
the
equation (just as
A-I
is
the
solution
to
AB
=
J)
that
allows one
to
immediately write down the solution
to
the equation (just as
we
could write down x = A
-lb).
3.
The
method
of
finite
elements:
This
is
a direct numerical method
that
can be used when (1) or (2) fails (or
is
intractable).
It
can be compared
with Gaussian elimination,
the
standard
direct numerical method for solving
Ax
=
h.
Like Gaussian elimination, finite element methods do not produce
a formula for the solution; however, again like Gaussian elimination, they are
broadly applicable.
