Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


t
In
this
book,
we
concentrate
on
Fourier series
and finite
element methods.
We
will
also
explain
the
idea
of a
Green's function
and
derive
a few
specific Green's
functions
that
we
will
find
useful.
3.7
Suggestions
for
further reading
A
good introductory
text,
which assumes
no
prior knowledge
of
linear algebra
and
is
written
at a
very accessible level,
is Lay
[34].
An
alternative
is
Strang
[44];
this
book also assumes
no
background
in
linear algebra,
but it is
written
at a
somewhat
more demanding level.
It is
noteworthy
for its
many insights
to the
applications
of
linear algebra
and for its
conversational tone.
A
more advanced
text
is
Meyer
[40].
Anyone
seriously interested
in
applied mathematics must become familiar with
the
computational aspects
of
linear algebra.
The
text
by
Strang mentioned above
includes material
on the
numerical aspects
of the
subject. There
are
also more
specialized references.
A
good introductory
text
is
Hager [23], while more advanced
treatments include Demmel [13]
and
Trefethen
and Bau
[49].
An
encyclopedic
reference
is
Golub
and Van
Loan
[19].
78
Chapter
3.
Essential linear algebra
In this book,
we
concentrate on Fourier series and finite element methods.
We
will also explain
the
idea of a Green's function and derive a
few
specific Green's
functions
that
we
will find useful.
3.7 Suggestions for further reading
A good introductory text, which assumes no prior knowledge of linear algebra and
is
written
at
a very accessible level,
is
Lay
[34].
An alternative
is
Strang
[44];
this
book also assumes no background in linear algebra,
but
it
is
written
at
a somewhat
more demanding level.
It
is
noteworthy for its many insights
to
the applications of
linear algebra
and
for its conversational tone. A more advanced text
is
Meyer
[40].
Anyone seriously interested in applied mathematics must become familiar with
the computational aspects of linear algebra. The
text
by Strang mentioned above
includes material on the numerical aspects of the subject. There are also more
specialized references. A good introductory
text
is
Hager
[23],
while more advanced
treatments include Demmel
[13]
and
Trefethen
and
Bau
[49].
An encyclopedic
reference
is
Golub and Van Loan
[19].

In an
ordinary
differential
equation
(ODE),
there
is a
single independent variable.
Commonly
ODEs model change over time,
so the
independent variable
is t
(time).
Our
interest
in
ODEs derives
from
the
following
fact:
both
the
Fourier series method
and the
finite
element method reduce time-dependent
PDEs
into
systems
of
ODEs.
In the
case
of the
Fourier series method,
the
system
is
completely decoupled,
so the
"system"
is
really just
a
sequence
of
scalar ODEs.
In
Section 4.2,
we
learn
how to
solve
the
scalar
ODEs
that
arise
in the
Fourier series method.
The
finite
element method,
on the
other hand, results
in
coupled systems
of
ODEs.
In
Section 4.3,
we
discuss
the
solution
of
linear, coupled systems
of first-
order ODEs. Although
we
present
an
explicit solution technique
in
that
section,
the
emphasis
is
really
on the
properties
of the
solutions,
as the
systems
that
arise
in
practice
are
destined
to be
solved
by
numerical
rather
than
analytical means.
In
Sections
4.4 and
4.5,
we
introduce some simple numerical methods
that
are
adequate
for
our
purposes.
We
close this chapter
by
interpreting
our
simple solutions
in
terms
of
Green's
functions.
Although
we do not
emphasize
the
method
of
Green's
function
in
this
book,
we do
explain
the
basic idea
in
Section 4.6.
Chapter
4
Jsseiitial
ordinary
equations
4.1
Converting
a
higher-order
equation
to a
first-order system
We
begin
our
discussion
of
ODEs with
a
simple observation:
It is
always possible
to
convert
a
single
ODE of
order
two or
more
to a
system
of first-order
ODEs.
We
illustrate this
on the
following
second-order equation:
We
define
79
differential
Chapter 4
tial ordinary
eal
equations
In an ordinary differential equation (ODE), there is a single independent variable.
Commonly ODEs model change over time,
so
the independent variable
is
t (time).
Our interest in ODEs derives from the following fact: both
the
Fourier series method
and the finite element method reduce time-dependent PDEs into systems of ODEs.
In the case of the Fourier series method,
the
system
is
completely decoupled,
so
the
"system"
is
really just a sequence of scalar ODEs.
In
Section 4.2,
we
learn
how
to
solve the scalar ODEs
that
arise in the Fourier series method.
The finite element method, on the other hand, results in coupled systems of
ODEs. In Section 4.3,
we
discuss the solution of linear, coupled systems of first-
order ODEs. Although
we
present an explicit solution technique in
that
section,
the emphasis
is
really on the properties of the solutions, as
the
systems
that
arise
in practice are destined
to
be solved by numerical rather
than
analytical means. In
Sections 4.4 and 4.5,
we
introduce some simple numerical methods
that
are adequate
for our purposes.
We
close this chapter by interpreting our simple solutions in terms of Green's
functions. Although
we
do not emphasize the method of Green's function in this
book,
we
do explain the basic idea in Section 4.6.
4.1 Converting a higher-order equation
to
a
first-order system
We
begin our discussion of ODEs with a simple observation:
It
is always possible
to convert a single ODE of order two or more
to
a system of first-order ODEs.
We
illustrate this on the following second-order equation:
cPu
du
a
dt
2
+ b
dt
+ cu = f(t).
(
4.1)
We
define
Xl
(t) = u(t),
79

80
Chapter
4.
Essential ordinary differential equations
Then
we
have
We
can
write this
as a first-order
system using matrix-vector notation:
In
(4.2),
x is the
vector-valued
function
The
same technique
will
convert
any
scalar equation
to a first-order
system.
If
the
unknown
is u and the
equation
is
order
m, we
define
The first m
—
1
equations
will
be
and the
last
equation
will
be the
original
ODE
(expressed
in the new
variables).
If
the
original scalar equation
is
linear, then
the
resulting system
will
also
be
linear,
and it can be
written
in
matrix-vector
form
if
desired.
An
mth-order
ODE
typically
has
infinitely
many solutions;
in
fact,
an
mth-
order linear
ODE has an
m-dimensional
subspace
of
solutions.
To
narrow
down
a
unique solution,
m
auxiliary conditions
are
required. When
the
independent
variable
is
time,
the
auxiliary conditions
are
initial
conditions:
These initial conditions
translate
immediately into initial conditions
for the new
unknowns
x\,
x%,...,
x
m
:
We
can
apply
a
similar technique
to
convert
an
mth-order system
of
ODEs
to a first-order
system.
For
example, suppose
x(i)
is a
vector-valued
function,
say
x(£)
6
R
n
.
Consider
a
second-order system:
80
Chapter
4.
Essential ordinary differential equations
Then
we
have
dXl
dt
=X2,
dX2
~u
C b du 1 c b 1
dt =
dt2
= --;;,u -
-;;,
dt + -;;,f(t) =
--;;,Xl
-
-;;,X2
+ -;;,f(t).
We
can write this as a first-order system using matrix-vector notation:
dx
[ 0
-d
=Ax+f(t),
A=
c
t
--
a
In (4.2), x
is
the
vector-valued function
(4.2)
The
same technique will convert any scalar equation
to
a first-order system.
If
the
unknown
is
u
and
the
equation
is
order m,
we
define
du
dm-lu
Xl
=
U,
X2
=
-d
'
...
,
Xm
=
-d
1 .
t t
m
-
The
first m - 1 equations will be
dx
l
dX2
dXm-l
dt
=
X2,
dt
=
X3,
... ,
---
=X
m
,
dt
and
the
last equation will be
the
original ODE (expressed in the new variables).
If
the
original scalar equation is linear,
then
the
resulting system will also be linear,
and
it
can be written in matrix-vector form if desired.
An mth-order ODE typically has infinitely many solutions; in fact,
an
mth-
order linear ODE has
an
m-dimensional subspace of solutions. To narrow down
a unique solution, m auxiliary conditions are required. When
the
independent
variable is time,
the
auxiliary conditions are initial conditions:
du
~-lU
u(to) = ao, dt
(to)
=
al,···,
dt
m
-
l
(to) =
am-l·
These initial conditions
translate
immediately into initial conditions for
the
new
unknowns
Xl,
X2,
...
,
Xm:
We
can apply a similar technique
to
convert an mth-order system of ODEs
to
a first-order system. For example, suppose
x(t)
is a vector-valued function, say
x(t)
ERn.
Consider a second-order system:
~x
(
dX)
dt
2
= f t, x, dt .
(4.3)

l.l.
Converting
a
higher-order equation
to a
first-order
system
81
We
define
We
then have
The
original
system
(4.3)
consists
of
n
second-order
ODEs
in
n
unknowns (the
components
of
x(i)).
We
have rewritten this original system
as
In
first-order
ODEs
in
In
unknowns (the
n
components
of
y(t)
and the n
components
of
z(t)).
The
fact
that
any ODE can be
written
as a first-order
system
has the
follow-
ing
benefit:
Any
theory
or
algorithm developed
for first-order
systems
of
ODEs
is
automatically
applicable
to any
ODE. This leads
to a
considerable simplification
in
the
study
of
this subject.
Exercises
1.
Write
the ODE
as a
system
of first-order
ODEs.
2.
Write
the ODE
as a
system
of first-order
ODEs.
3.
Write
the ODE
4.
Write
the ODE
as a
system
of first-order
ODEs.
as a
system
of first-order
ODEs.
5.
Write
the
following
system
of
second-order ODEs
as a
system
of first-order
ODEs:
4.1. Converting a higher-order equation
to
a first-order system
We
define
We
then have
yet) = x(t),
dx
z(t) = dt (t).
dy
dt = z,
dz
dt =
f(t,y,z).
81
The original system (4.3) consists of n second-order ODEs in n unknowns (the
components of
x(
t)).
We
have rewritten this original system as
2n
first-order ODEs
in
2n
unknowns (the n components of yet)
and
the
n components of z(t)).
The fact
that
any ODE can be written as a first-order system has the
follow-
ing benefit: Any theory or algorithm developed for first-order systems of ODEs
is
automatically applicable
to
any ODE. This leads to a considerable simplification in
the
study of this subject.
Exercises
1. Write the ODE
rPu
2 dx
2
+ u = 0
as a system of first-order ODEs.
2.
Write the ODE
rPu
dx
2
+ csin (u) = 0
as a system of first-order ODEs.
3.
Write the ODE
d
4
u d
2
u
dt
4
-
2 dt
2
+ u = sin (t)
as a system of first-order ODEs.
4.
Write the ODE
d
2
u du 2
-
-2u-
+t
u=O
dt
2
dt
as a system of first-order ODEs.
5.
Write the following system of second-order ODEs as a system of first-order
ODEs:

so
we
will
present
a
simple method
for
computing
its
general solution.
The
method
is
based
on the
following
idea: When
faced
with
a
differential
equation,
one can
sometimes guess
the
general
form
of the
solution and,
by
substituting this general
form
into
the
equation, determine
the
specific
form.
In
this case,
we
assume
that
the
solution
of
(4.4)
is of the
form
We
distinguish three cases.
1.
The
characteristic
roots
are
real
and
unequal
(i.e.
6
2
—
4ac > 0). In
this case, since
the
equation
is
linear,
any
linear combination
of
e
rit
and
e
r2t
is
also
a
solution
of
(4.4).
In
fact,
as we now
show, every solution
of
(4.4)
can
be
written
as
4.2.1
The
general solution
of a
second-order homogeneous
ODE
with
constant coefficients
In the
ensuing chapters,
we
will
often
encounter
the
second-order linear homoge-
neous
ODE
with constant
coefficients,
4.2
Solutions
to
some simple
ODEs
In
this section,
we
show
how to
solve some simple
first- and
second-order ODEs
that
will
arise
later
in the
text.
Here
mi
and
m^
are
constants,
and
j\
and
/2
are
real-valued
functions
of
four
variables.
82
Chapter
4.
Essential ordinary
differential
equations
Substituting into (4.4) yields
since
the
exponential
is
never zero, this equation holds
if and
only
if
This quadratic
is
called
the
characteristic polynomial
of the ODE
(4.4),
and its
roots
are
called
the
characteristic
roots
of the
ODE.
The
characteristic roots
are
given
by the
quadratic formula:
82
Chapter
4.
Essential ordinary differential equations
Here
ml
and
m2
are constants, and
II
and
fz
are real-valued functions of four
variables.
4.2 Solutions
to
some simple ODEs
In this section,
we
show how to solve some simple first- and second-order ODEs
that
will arise later in
the
text.
4.2.1 The general solution
of
a second-order homogeneous
ODE
with constant coefficients
In
the
ensuing chapters,
we
will often encounter the second-order linear homoge-
neous ODE with constant coefficients,
d2u du
a dt
2
+ b dt +
cu
= 0,
(4.4)
so
we
will present a simple method for computing its general solution. The method
is
based on
the
following idea: When faced with a differential equation, one can
sometimes guess the general form of
the
solution and, by substituting this general
form into
the
equation, determine
the
specific form.
In this case,
we
assume
that
the
solution of (4.4)
is
of
the
form
Substituting into (4.4) yields
since the exponential
is
never zero, this equation holds if and only if
ar2
+
br
+ c =
O.
This quadratic
is
called the characteristic polynomial of
the
ODE (4.4), and its roots
are called
the
characteristic roots of
the
ODE.
The characteristic roots are given by
the
quadratic formula:
-b
- Vb
2
-
4ac
-b
+ v'b
2
-
4ac
rl
= ,
r2
=
2a
2a
We
distinguish three cases.
1.
The
characteristic
roots
are
real
and
unequal
(Le. b
2
-
4ac
>
0).
In
this case, since
the
equation
is
linear, any linear combination of e
r1t
and e
r2t
is
also a solution of (4.4). In fact, as
we
now show, every solution of (4.4) can
be written as
(4.5)

4.2.
Solutions
to
some
simple
ODEs
83
for
some choice
of
ci,
C2-
In
fact,
we
will
show
that,
for any
&i,
£2,
the
initial
value problem
(IVP)
has a
unique solution
of the
form
(4.5).
With
u
given
by
(4.5),
we
have
and we
wish
to
choose
c\,
c^
to
satisfy
that
is,
The
coefficient
matrix
in
this equation
is
obviously nonsingular (since
r\
/
r-2),
and so
there
is a
unique solution
c\,C2
for
each
fci, fo •
Since
every solution
of
(4.4)
can be
written
in the
form
(4.5),
we
call (4.5)
the
qeneral
solution
of
(4.4).
2.
The
characteristics
roots
are
complex
(i.e.
b
2
— 4ac < 0). In
this
case,
the
characteristics
roots
are
also unequal;
in
fact, they
form
a
complex
conjugate
pair.
The
analysis
of the
previous case applies,
and we
could write
the
general solution
in the
form
(4.5)
in
this case
as
well. However, with
7*1,
r<2
complex,
e
ri
*,e
r2
*
are
complex-valued functions,
and
this
is
undesirable.
and so
This shows (because
the
equation
is
linear)
that
4.2. Solutions
to
some simple ODEs 83
for some choice of
Cl,
C2.
In
fact,
we
will show
that,
for any
kl'
k2,
the
initial
value problem (IVP)
d
2
u
du
a
dt
2
+ b
dt
+ cu = 0,
u(O)
=
kl'
du(O)
= k
dt 2
has a unique solution of the form (4.5).
With
u given by (4.5),
we
have
u(O)
=
CI
+
C2,
du
dt (0) =
rlCI
+
r2
C
2,
and
we
wish to choose
CI,
C2
to satisfy
that
is,
CI
+
C2
=
kl'
rlCI
+
r2C2
= k2'
[
ll]C_k
rl
r2
(4.6)
The
coefficient matrix in this equation
is
obviously nonsingular (since
rl
:j:.
r2),
and
so
there
is
a unique solution
CI,
C2
for each
kl'
k
2
.
Since every solution of
(4.4)
can be written in the form (4.5),
we
call
(4.5)
the
general solution of (4.4).
2.
The
characteristics
roots
are
complex
(Le. b
2
-
4ac
< 0).
In
this
case, the characteristics roots are also unequal; in fact, they form a complex
conjugate pair. The analysis of the previous case applies, and
we
could write
the general solution in the form
(4.5) in this case as well. However, with
rl,
r2
complex, e
T1
t
,e
T2t
are complex-valued functions, and this
is
undesirable.
With
rl
=
f.L
-
Ai,
r2
=
f.L
+
Ai,
we
have (by Euler's formula)
and so
e
T1t
= el-'t (cos
(At)
- i sin (At)),
e
T2t
= el-'t (cos
(At)
+ i sin (At)),
1
2"
(eTlt+eT2t)
=
el-'t
cos (At),
~
(e
T1t
_ e
T2t
)
= el-'t sin (At).
This shows (because
the
equation
is
linear)
that
el-'t
cos (At),
el-'t
sin
(At)

Therefore
this
example
falls
in
case
2
above,
and the
general
solution
of
the ODE is
Example
4.2.
The ODE
84
Chapter
4.
Essential
ordinary
differential
equations
are
also solutions
of
(4.4)
in
this
case.
We
will
write
the
general solution
in
the
form
As
in the
previous
case,
we can
show
that
every
solution
of
(4.4)
can be
written
in
this
form
(see
Exercise
2).
3.
The
characteristic polynomial
has a
single (repeated) real root
(i.e.
b
2
— 4ac = 0). In
this case
the
root
is r —
—b/(2a).
We
cannot write
the
general solution with
the
single solution
e
rt
;
by an
inspired guess,
we try
te
rt
as the
second solution. Indeed, with
u(t)
—
te
rt
,
we
have
and so
Example
4.1.
The
characteristic polynomial
of
This shows
that
te
rt
is
also
a
solution
of
(4.4),
and we
write
the
general
solution
in
this case
as
where
r =
—b/(2a).
Once again,
it is not
hard
to
show
that
every solution
of
(4.4)
can be
written
in
this
form
(see
Exercise
3).
is
r
2
—
r +
I,
which
has
roots
84
Chapter
4.
Essential ordinary differential equations
are also solutions of (4.4) in this case.
We
will write the general solution in
the
form
Cle
Pt
cos (At) +
C2ept
sin (At).
As
in the previous case,
we
can show
that
every solution of (4.4) can be written
in this form (see Exercise 2).
3.
The
characteristic
polynomial
has
a
single
(repeated)
real
root
(Le.
b
2
-
4ac
=
0).
In this case
the
root
is
r =
-b/(2a).
We
cannot write the
general solution with the single solution
e
Tt
; by an inspired guess,
we
try
teTt
as the second solution. Indeed, with
u(t)
= teTt,
we
have
du
~u
dt (t) =
(1
+
rt)e
Tt
, dt
2
(t) =
(2
+
rt)re
Tt
,
and
so
~u
du
a dt
2
(t) + b dt (t) + cu(t)
= a(2 +
rt)re
Tt
+
b(1
+
rt)e
Tt
+ cte
Tt
= (ar2 +
br
+
c)
teTt
+ (2ar +
b)
e
Tt
= 0 (since ar2 +
br
+ c = 0
and
2ar + b = 2a(
-b/(2a))
+ b = 0).
This shows
that
teTt
is
also a solution of (4.4),
and
we
write the general
solution in this case as
where r
=
-b/(2a).
Once again, it
is
not hard to show
that
every solution of
(4.4) can be written in this form (see Exercise 3).
Example
4.1.
The characteristic polynomial
of
~u
du
---+u=O
dt
2
dt
is
r2
- r + 1, which has roots
1
v'3.
1
v'3.
rl
= - +
-z
r2
= - -
-z.
2
2'
2 2
Therefore this example falls
in
case 2 above, and the general solution
of
the
ODE
is
( (
v'3
t
) .
(v'3
t
) )
u(t)
=
Cl
cos 2 + C2
sm
-2-
e
t
/
2
•
Example
4.2.
The
ODE
~u
du
--2-+u=0
dt
2
dt

The
coefficient
0
2
is a
positive real number.
In
this
section,
we
will present
a
surprisingly
simple formula
for the
solution.
By
the
principle
of
superposition,
we can
solve
the two
IVPs
4.2.
Solutions
to
some simple ODEs
85
has
characteristic polynomial
r
2
—
2r +
1.
The
characteristic
roots
are
so
case
3
above
applies.
The
general solution
is
4.2.2
A
special inhomogeneous second-order linear
ODE
In
Chapter
7, we
will
encounter
the
following
inhomogeneous
IVP:
ri
=
r
2
= 1,
and
and add the
solutions
to get the
solution
to
(4.7).
It is
straightforward
to
apply
the
techniques
of
Section 4.2.1
to
derive
the
solution
of
(4.8):
(see
Exercise
12).
The
solution
of
(4.9)
is
more
difficult
to
derive, although
the final
answer
has
a
pleasingly simple
form:
4.2. Solutions
to
some simple ODEs
has
characteristic polynomial r2 -
2r
+ 1.
The
characteristic
roots
are
so
case
3
above
applies.
The
general solution is
4.2.2 A special inhomogeneous second-order linear
ODE
In
Chapter
7,
we
will encounter
the
following inhomogeneous IVP:
d
2
u
dt
2
+
()2U
= f(t),
u(t
o
)
=
a,
du
dt
(to)
=
{3.
85
(4.7)
The
coefficient
()2
is
a positive real number.
In
this
section, we will present a
surprisingly simple formula for
the
solution.
and
By
the
principle of superposition, we
can
solve
the
two
IVPs
~u
2
dt
2
+
()
u = 0,
u(to) =
a,
du
dt (to)
=
{3
d
2
u
dt
2
+
(Pu
= f(t),
u(to)
= 0,
du
dt
(to)
= 0
(4.8)
(4.9)
and add
the
solutions
to
get
the
solution
to
(4.7).
It
is straightforward
to
apply
the
techniques of Section 4.2.1
to
derive
the
solution
of
(4.8):
Ul
(t) = a cos
(()(
t - to)) +
~
sin
(()(
t - to))
(4.10)
(see Exercise 12).
The
solution of (4.9)
is
more difficult
to
derive,
although
the
final answer has
a pleasingly simple form:
llt
U2(t)
=
(j
sin
(()(t
-
s))f(s)
ds.
to
(4.11)
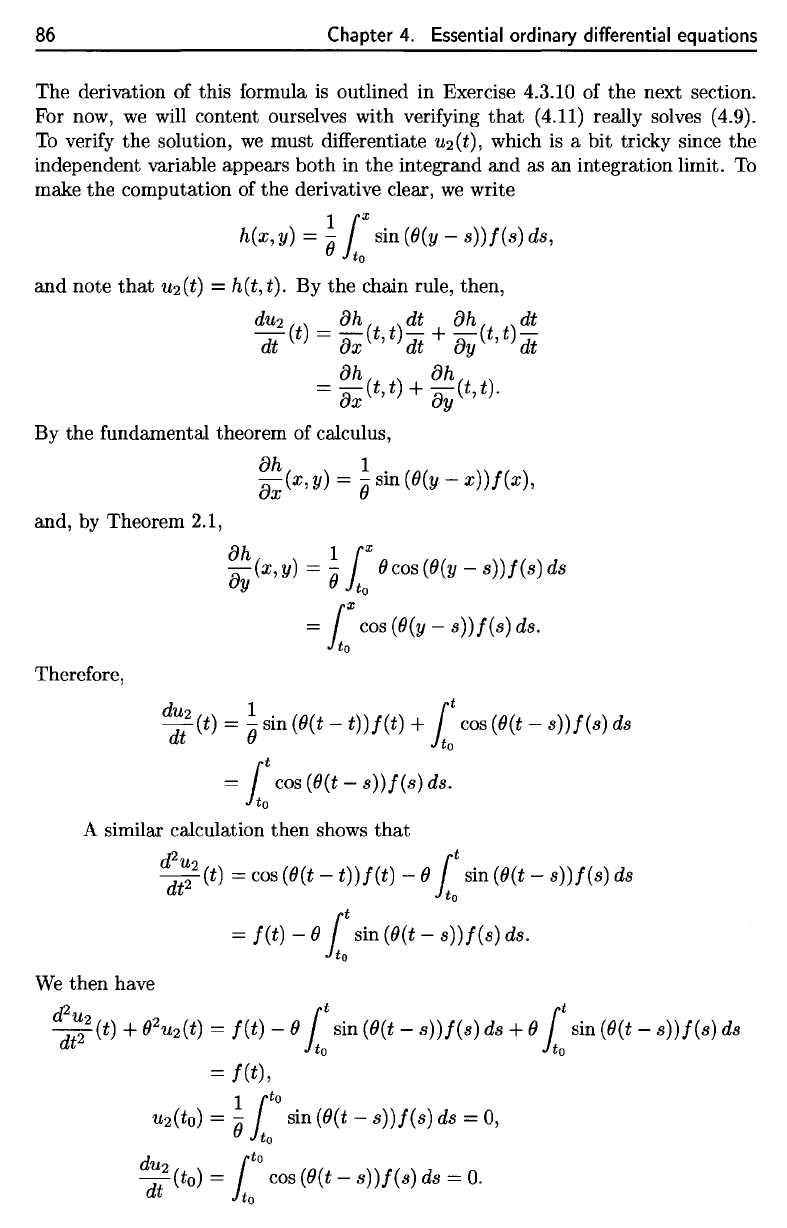
86
Chapter
4.
Essential ordinary differential equations
The
derivation
of
this formula
is
outlined
in
Exercise 4.3.10
of the
next section.
For
now,
we
will
content ourselves with
verifying
that
(4.11) really solves (4.9).
To
verify
the
solution,
we
must differentiate
W2(i),
which
is a bit
tricky since
the
independent variable
appears
both
in the
integrand
and as an
integration limit.
To
make
the
computation
of the
derivative clear,
we
write
and
note
that
u^t)
=
h(t,t).
By the
chain rule, then,
By
the
fundamental theorem
of
calculus,
and,
by
Theorem
2.1,
Therefore,
A
similar calculation then shows
that
We
then have
86
Chapter
4.
Essential
ordinary
differential
equations
The derivation of this formula
is
outlined in Exercise 4.3.10 of the next section.
For now,
we
will content ourselves with verifying
that
(4.11) really solves (4.9).
To verify the solution,
we
must differentiate
U2(t),
which
is
a bit tricky since the
independent variable appears
both
in the integrand
and
as
an
integration limit. To
make the computation of the derivative clear,
we
write
11
X
h(x,y) = (j sin
(O(y
-
s))f(s)ds,
to
and
note
that
U2(t)
= h(t, t). By the chain rule, then,
dU2
ah dt ah
dt
di(t)
=
ax
(t, t) dt + ay
(t,
t) dt
ah ah
=
ax
(t, t) + ay (t, t).
By the fundamental theorem
of
calculus,
~~
(x,
y)
=
~
sin
(O(y
-
x))f(x),
and, by Theorem 2.1,
ah
11
x
a(x,y)
= (j o cos
(O(y
-
s))f(s)ds
y to
= l
x
cos
(O(y
-
s))f(s)
ds.
to
Therefore,
dU2
1.
rt
dt (t) = (j sm
(O(t
-
t))f(t)
+
lto
cos
(O(t
-
s))f(s)
ds
=
it
cos
(O(t
-
s))f(s)
ds.
to
A similar calculation then shows
that
We
then
have
~u
it
d
22
(t)
= cos
(O(t
-
t))f(t)
- 0 sin
(O(t
-
s))f(s)
ds
t to
= f(t) - 0 t sin
(O(t
-
s))f(s)
ds.
lto
~~2
(t) +
02
U2
(t)
=
f(t)
- 0
rt
sin
(O(t
-
s))f(s)
ds
+ 0
rt
sin
(O(t
-
s))f(s)
ds
t
lto
lto
= f(t),
lito
U2(tO)
= (j sin
(O(t
-
s))f(s)
ds
= 0,
to
du ito
d
2
(to)
= cos
(O(t
-
s))f(s)
ds
=
O.
t to

4.2.
Solutions
to
some
simple
ODEs
87
Thus
U2
solves (4.9), which
is
what
we
wanted
to
show.
We
have
now
shown
that
the
solution
to
(4.7)
is
(the
integral
can be
computed
using
the
subtraction formula
for
sine
and
simplified
using
other trigonometric
identities).
Example
4.3.
The
solution
to
i<t
to
4.2.3 First-order linear ODEs
Another type
of ODE for
which
we can find the
general solution
is the first-order
linear
ODE:
(We
could
treat
the
case
of a
nonconstant
coefficient
similarly; however,
we
have
n
need
to.)
The
solution
is
based
on the
idea
of an
integrating factor:
we
multiply
th
equation
by a
special function
that
allows
us to
solve
by
direct integration.
We not
that
Therefore,
we
have
This
immediately gives
us the
solution
to the
IVP
4.2. Solutions
to
some
simple ODEs
Thus
U2
solves (4.9), which
is
what
we
wanted
to
show.
We
have now shown
that
the solution to (4.7)
is
(3
lit
u(t) = a cos
(O(t
- to)) +
7i
sin
(O(t
- to)) +
(j
sin
(O(t
-
s))f(s)
ds.
to
EXaJIlple
4.3.
The solution to
is
~u
dt
2
+ u = cos (t),
u(O)
= 0,
du(O)
= 0
dt
u(t)
= lot sin (t -
s)
cos
(s)
ds
=
~
sin
(t)
87
( 4.12)
(the integml can
be
computed using the subtmction formula for sine and simplified
using other trigonometric identities).
4.2.3 First-order
linear
ODEs
Another type of ODE for which
we
can find the general solution is the first-order
linear ODE:
du
dt - au =
f(t).
( 4.13)
(We could
treat
the
case of a nonconstant coefficient similarly; however,
we
have no
need to.)
The solution is based on the idea of an integmting factor:
we
multiply the
equation by a special function
that
allows us to solve by direct integration.
We
note
that
Therefore,
we
have
du du
- - au = f(t)
=}
e-
at
_ - ae-atu =
e-atf(t)
dt dt
d
=}
- [e-atu(t)] =
e-
at
f(t)
dt
=}
e-atu(t) = e-atOu(to) +
it
e-
as
f(s)
ds
to
=}
u(t) = ea(t-to)u(to) +
it
ea(t-s) f(s) ds.
to
This immediately gives us the solution to the IVP
du
dt - au = f(t),
u(to)
=
Uo.
(4.14)
