Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


88
Chapter
4.
Essential ordinary
differential
equations
Example
4.4.
The
IVP
(the
integral
can be
computed
by two
applications
of
integration
by
parts).
It
should
be
appreciated
that,
although
we
have
an
explicit formula
for the
solution
of
(4.13),
it
will
be
impossible
in
many cases
to
explicitly evaluate
the
integrals involved
in
terms
of
elementary functions.
Exercises
1.
Let 5 be the
solution
set of
(4.4).
(a)
Show
that
S is a
subspace
of C
2
(R),
the set of
twice-continuously
differ-
entiable
function
defined
on R.
(b)
Use the
results
of
this section
to
show
S is
two-dimensional
for any
values
of
a, 6, and c,
provided only
that
a
^
0.
has
solution
2.
Suppose
(4.4)
has
characteristic roots
/z±
\i,
where
/i,
A
e
R and A
/
0.
Show
that,
for any
ki,
£2,
there
is a
unique choice
of
ci,
C2
such
that
the
solution
oi
(4.6)
is
3.
Suppose
(4.4)
has the
single characteristic root
r =
-b/(2a).
Show
that,
for
any fei, fo,
there
is a
unique choice
of
ci,C2
such
that
the
solution
of
(4.6)
is
4.
For
each
of the
following
IVPs,
find the
general solution
of the ODE and use
it
to
solve
the
IVP:
88
Chapter
4.
Essential ordinary differential equations
Example
4.4.
The
IVP
has solution
du .
()
dt
+u
= sm
t,
u(O)
= 2
u(t)
=
2e-
t
+
lot
e-(t-s)
sin
(s)
ds
1
=
2e-
t
+
'2
(sin (t) - cos (t) +
e-
t
)
=
~e-t
+
~
(sin (t) - cos(t))
(the integral can
be
computed by two applications
of
integration
by
parts).
It
should
be
appreciated
that,
although
we
have
an
explicit formula for
the
solution of (4.13),
it
will
be
impossible in
many
cases
to
explicitly evaluate
the
integrals involved
in
terms of elementary functions.
Exercises
1. Let S
be
the
solution set
of
(4.4).
(a) Show
that
S is a subspace
of
C
2
(R),
the
set of twice-continuously differ-
entiable function defined
on
R.
(b) Use
the
results of this section
to
show S is two-dimensional for
any
values
of a,
b,
and
c, provided only
that
a ¥
O.
2. Suppose (4.4) has characteristic roots
/-l±>..i,
where
/-l,
>..
E
Rand>..
¥
O.
Show
that,
for any
kl'
k2, there is a unique choice of
Cl,
C2 such
that
the
solution of
(4.6) is
CleP,t
cos
(>..t)
+
C2eP,t
sin
(>..t).
3.
Suppose (4.4) has
the
single characteristic
root
r =
-bj(2a).
Show
that,
for
any
kl'
k2'
there
is a unique choice of
Cl,
C2
such
that
the
solution of (4.6) is
Clert +
C2
tert
.
4.
For each of
the
following IVPs, find
the
general solution of
the
ODE
and
use
it
to
solve
the
IVP:
(a)
d
2
u du
dt
2
+ 2 dt + u = 0,
u(O)
= 1,
du(O)
= 0
dt

4.2. Solutions
to
some simple
ODEs
89
5.
The
following
differential
equations
are
accompanied
by
boundary
conditions—
auxiliary conditions
that
refer
to the
boundary
of a
spatial
domain
rather
than
to an
initial time.
By
using
the
general solution
of the
ODE, determine
whether
a
nonzero solution
to the
boundary value
problem (BVP) exists,
and
if
so,
whether
the
solution
is
unique.
4.2. Solutions
to
some simple ODEs
(b)
dlu
du
3 dt
2
+ 2 dt + u = 0,
(c)
(d)
u(o) =
-1,
du(O)
= 3
dt
dlu
du
2 dt
2
+ 2 dt + u = 0,
u(O)
= 0,
du
(0)
= 1
dt
d
2
u
du
dt
2
+ 3 dt + u = 0,
u(O)
= 1,
du
(0)
= 2
dt
89
5.
The
following differential equations are accompanied by boundary
conditions-
auxiliary conditions
that
refer
to
the boundary of a spatial domain
rather
than
to
an
initial time. By using
the
general solution of
the
ODE, determine
whether a nonzero solution
to
the
boundary value problem (BVP) exists, and
if so, whether
the
solution
is
unique.
(a)
(b)
(c)
d
2
u
dx
2
-
2u = 0,
u(O)
= 0,
u(l)
= 0
d
2
u
dx
2
+ 2u = 0,
u(O)
= 0,
u(l)
= 0
dlu
2
dx
2
+ 7r U = 0,
u(O)
= 0,
u(l)
= 0

90
Chapter
4.
Essential
ordinary
differential
equations
6.
Determine
the
values
of A
e
R
such
that
the BVP
has a
nonzero solution.
7.
Prove directly
(that
is, by
substituting
u
into
the
differential
equation
and
initial condition)
that
solves
8.
Solve
the
following
IVPs:
9.
Find
the
solution
to the
IVP
90
Chapter
4.
Essential ordinary differential equations
6. Determine the values of A E R such
that
the
BVP
d
2
u
dx
2
+
AU
= 0,
has a nonzero solution.
u(o)
= 0,
u(l)
= °
7.
Prove directly
(that
is, by substituting u into
the
differential equation and
initial condition)
that
u(t)
= ea(t-to)uo +
it
ea(t-s)
/(s)
ds
to
solves
8. Solve the following IVPs:
(a)
(b)
(c)
9.
Find the solution
to
the IVP
du
dt - au =
/(t),
u(t
o
)
=
Uo·
du
dt = 2u - 0.1,
u(O)
= 1.0
du
dt =
-2u
+ O.lt,
u(O)
= 0
du
dt
+u
= t,
u(O)
= 0
~u
dt
2
+ 4u = 1,
u(o)
= 0,
du
dt
(0)
=
O.

4.3. Linear systems
with
constant
coefficients
91
10.
Find
the
solution
to the
IVP
11.
Find
the
solution
to the IVP
12.
Use the
techniques
of
Section 4.2.1
to
derive
the
solution
to
(4.8),
and
verify
that
you
obtain (4.10). (Hint:
One way to do
this
is to
write
the
general
solution
of the ODE as
u(t)
=
c\
cos
(9t]
+
02
sin
(Ot)
and
then solve
for
c\
and
C2-
If you do
this,
you
will
then have
to
apply trigonometric identities
to put the
solution
in the
form
given
in
(4.10).
It is
simpler
to
recognize
at the
beginning
that
the
general solution could just
as
well
be
written
as
u(t)
=
ci
cos
(0(t
-
t
0
})
+
c
2
sin
(0(t
-
t
0
)).)
4.3
Linear
systems
with constant coefficients
We
now
consider
a first-order
linear system
of
ODEs with constant
coefficients.
Such
a
system
can be
written
As
with
a
linear algebraic system, there
is a
great
advantage
in
using
matrix-vector
notation.
System (4.15)
can be
written
as
where
4.3. Linear systems with constant coefficients
10.
Find
the
solution to the IVP
11. Find
the
solution
to
the IVP
d
2
u
dt
2
+ 9u =
t,
d
2
u
u(O)
= 0,
du(O)
=
O.
dt
-t
dt
2
+u
= e ,
u(O)
= 1,
du(O)
=
O.
dt
91
12. Use the techniques of Section 4.2.1
to
derive
the
solution to (4.8), and verify
that
you obtain (4.10). (Hint: One way
to
do this
is
to
write the general
solution of
the
ODE as u(t) =
Cl
cos
(Ot)
+
C2
sin
(Ot)
and then solve for
Cl
and
C2.
If
you do this, you will
then
have to apply trigonometric identities
to
put
the
solution in
the
form given in (4.10).
It
is
simpler
to
recognize
at
the beginning
that
the general solution could
just
as
well
be written as
u(t) =
Cl
cos
(O(t
- to)) + C2 sin
(O(t
- to)).)
4.3
Linear
systems with constant coefficients
We
now consider a first-order linear system of ODEs with constant coefficients.
Such a system can be written
dXl
dt
=
anXl
+
a12
X
2
+
...
+ alnX
n
+
/1
(t),
dX2
dt
=
a21
X
l
+
a22
x
2
+
...
+
a2n
X
n
+
h(t),
(4.15)
dX
n
(it
= anlXl + a
n
2
X
2 +
...
+
annXn
+ fn(t).
As with a linear algebraic system, there
is
a great advantage in using matrix-vector
notation. System (4.15) can be written as
dx
(4.16) -
=Ax+f(t),
dt
where
an
a12
al
n
1 [
x,(t)
1 [
j,(t)
1
a21
a22
a2n
X2(t)
h(t)
A=
. , x(t) = . , f(t) = . .
anl
a
n
2
a~n
xn·(t)
fn·(t)
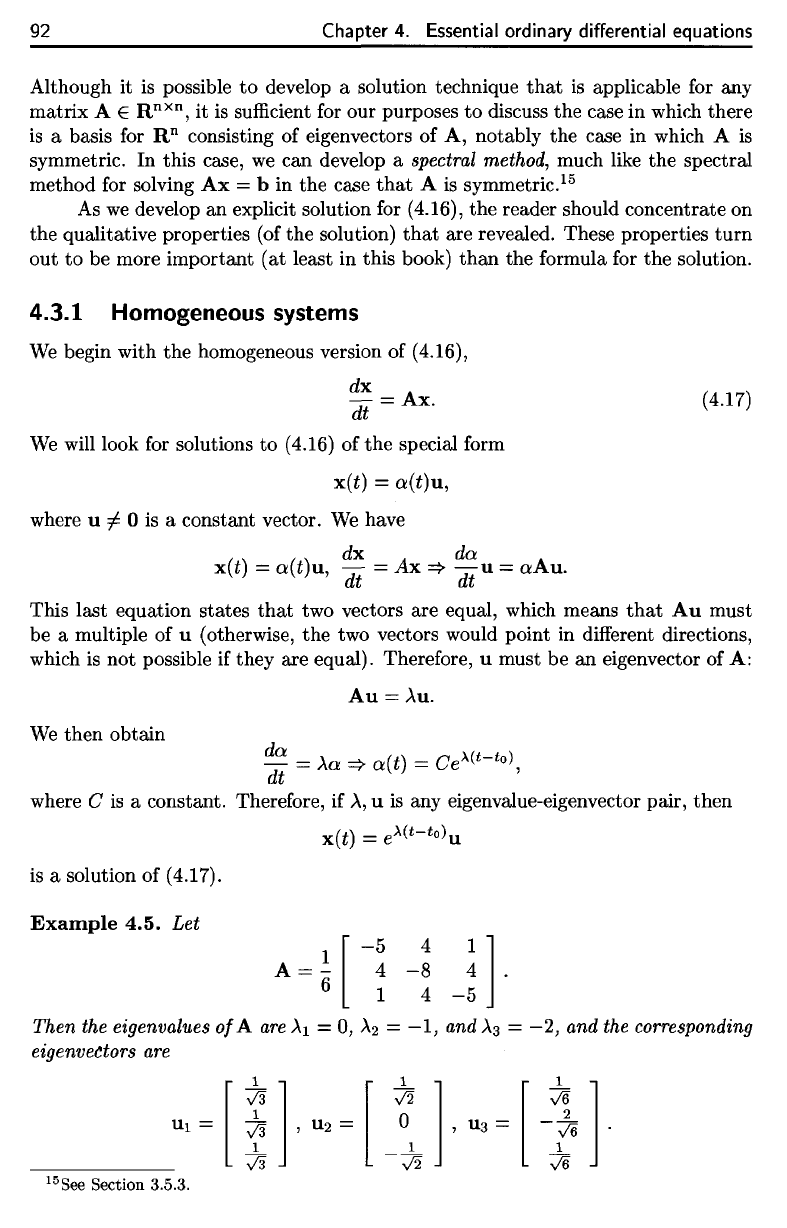
92
Chapter
4.
Essential
ordinary
differential
equations
Although
it is
possible
to
develop
a
solution technique
that
is
applicable
for any
matrix
A €
R
nxn
,
it is
sufficient
for our
purposes
to
discuss
the
case
in
which there
is
a
basis
for
R
n
consisting
of
eigenvectors
of A,
notably
the
case
in
which
A is
symmetric.
In
this case,
we can
develop
a
spectral
method,
much like
the
spectral
method
for
solving
Ax = b in the
case
that
A is
symmetric.
15
As
we
develop
an
explicit solution
for
(4.16),
the
reader should concentrate
on
the
qualitative properties
(of the
solution)
that
are
revealed. These properties turn
out to be
more important
(at
least
in
this book) than
the
formula
for the
solution.
We
then obtain
where
C is a
constant. Therefore,
if
A,
u is any
eigenvalue-eigenvector pair, then
Example
4.5.
Let
Then
the
eigenvalues
of
A are
\i
=
0,
A2
=
—1,
and
AS
=
—2,
and the
corresponding
eigenvectors
are
15
See
Section
3.5.3.
is
a
solution
of
(4.17).
This
last
equation
states
that
two
vectors
are
equal, which means
that
Au
must
be a
multiple
of u
(otherwise,
the two
vectors would point
in
different
directions,
which
is not
possible
if
they
are
equal). Therefore,
u
must
be an
eigenvector
of A:
4.3.1 Homogeneous
systems
We
begin with
the
homogeneous version
of
(4.16),
We
will
look
for
solutions
to
(4.16)
of the
special
form
where
u
^
0 is a
constant vector.
We
have
92
Chapter
4.
Essential ordinary differential equations
Although it
is
possible
to
develop a solution technique
that
is
applicable for any
matrix A
E
Rnxn,
it
is
sufficient for our purposes
to
discuss
the
case in whkl1 there
is
a basis for R
n
consisting of eigenvectors of
A,
notably the case in which A
is
symmetric. In this case,
we
can develop a
spectral
method, much like the spectral
method for solving
Ax
= b in the case
that
A
is
symmetric.
15
As
we
develop an explicit solution for (4.16), the reader should concentrate on
the qualitative properties (of
the
solution)
that
are revealed. These properties
turn
out
to
be more important (at least in this book)
than
the formula for the solution.
4.3.1 Homogeneous
systems
We
begin with the homogeneous version of (4.16),
dx
dt
=
Ax.
We
will look for solutions
to
(4.16) of
the
special form
x(t) = a(t)u,
where
uf:.O
is
a constant vector.
We
have
dx da
x(t)
= a(t)u, dt =
Ax
=>
dt
u =
aAu.
(4.17)
This last equation states
that
two vectors are equal, which means
that
Au
must
be a multiple of u (otherwise,
the
two vectors would point in different directions,
which
is
not possible if they are equal). Therefore, u must be an eigenvector of A:
Au=)"u.
We
then obtain
da = ),,0:
=>
a(t) = Ce),(t-to)
dt
'
where C
is
a constant. Therefore, if
)",
u
is
any eigenvalue-eigenvector pair, then
x(t) =
e),(t-to)u
is
a solution of (4.17).
Example
4.5.
Let
A =
~
[-:
-:
!
].
6 1
4-5
Then the eigenvalues of A
are),,1
= 0,
),,2
=
-1,
and),,3
=
-2,
and
the
corresponding
eigenvectors
are
15S
ee
Section 3.5.3.

4.3. Linear systems
with
constant
coefficients
93
We
therefore
know
three
independent solutions
of
namely,
If,
as in the
previous example,
there
is a
basis
for
R
n
consisting
of
eigenvectors
{ui,
u
2
,...,
u
n
}
of A,
with corresponding eigenvalues
AI,
A
2
,...,
A
n
,
then
we can
write
the
general solution
of
(4.17).
Indeed,
it
suffices
to
show
that
we can
solve
We
also have
by
construction.
Example
4.6.
Let A be the
matrix
in
Example
4-5,
and let
Since
{ui,
112,...,
u
n
}
is a
basis
for
R
n
,
there
exists
a
vector
c G
R
n
such
that
The
solution
to
(4.18)
is
then
4.3. Linear systems with constant coefficients
93
We therefore know three independent solutions
of
dx
dt =
Ax,
namely,
X1(t)=U1,
X2(t)
=
e-(t-t
O
)U2,
X3(t)
=
e-
2
(t-t
O
)U3.
If, as in the previous example, there
is
a basis for R n consisting of eigenvectors
{U1'
U2,
...
, un} of
A,
with corresponding eigenvalues
AI,
A2,""
An,
then
we
can
write the general solution of
(4.17). Indeed, it suffices
to
show
that
we
can solve
dx
-A
dt -
x,
x(to) =
Xo·
(4.18)
Since
{U
1,
U2,
...
,
Un}
is
a basis for R
n,
there exists a vector c
ERn
such
that
The solution to
(4.18)
is
then
(4.19)
This
is
verified by computing
dx/
dt:
~~
(t) = cIAle
A1
(t-t
o
)UI
+
c2A2eA2(t-to)U2
+ ... +
CnAneAn(t-to)un
=
cle),dt-to)
AUI +
c2e),2(t-t
O
)
AU2
+ ... +
cne),n(t-t
o
)
AU
n
= A
(C1e),1(t-to)U1
+
c2e
A2
(t-t
o
)U2
+ ... +
CneAn(t-tO)un)
=
Ax(t).
We
also have
by construction.
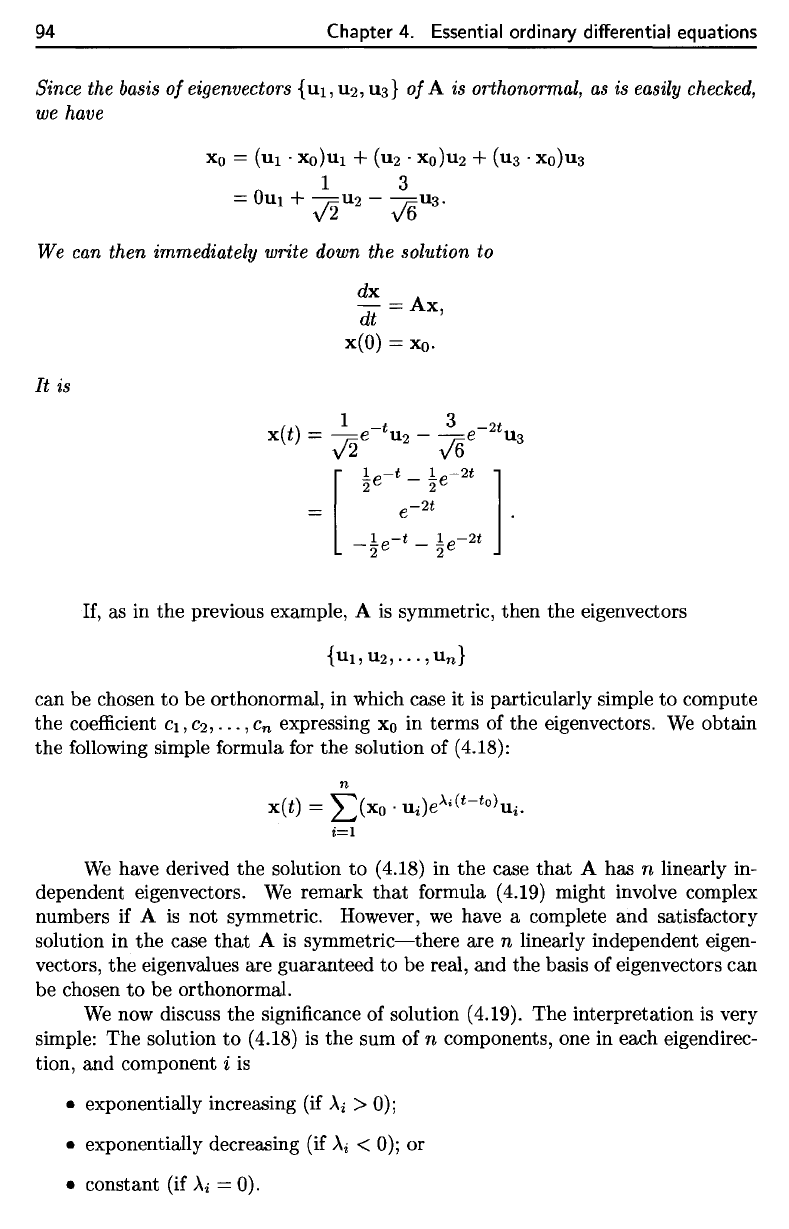
Example
4.6.
Let
A
be
the matrix in Example
4.5,
and let
94
Chapter
4.
Essential ordinary differential equations
Since
the
basis
of
eigenvectors
{111,112,113}
o/A
is
orthonormal,
as is
easily
checked,
we
have
It is
If,
as in the
previous example,
A is
symmetric,
then
the
eigenvectors
{ui,u
2
,...,u
n
}
We
have derived
the
solution
to
(4.18)
in the
case
that
A has n
linearly
in-
dependent eigenvectors.
We
remark
that
formula (4.19) might involve complex
numbers
if A is not
symmetric. However,
we
have
a
complete
and
satisfactory
solution
in the
case
that
A is
symmetric—there
are n
linearly independent eigen-
vectors,
the
eigenvalues
are
guaranteed
to be
real,
and the
basis
of
eigenvectors
can
be
chosen
to be
orthonormal.
We
now
discuss
the
significance
of
solution (4.19).
The
interpretation
is
very
simple:
The
solution
to
(4.18)
is the sum of n
components,
one in
each eigendirec-
tion,
and
component
i is
We
can
then immediately write
down
the
solution
to
can
be
chosen
to be
orthonormal,
in
which case
it is
particularly simple
to
compute
the
coefficient
ci,C2,..
-
,c
n
expressing
x
0
in
terms
of the
eigenvectors.
We
obtain
the
following
simple formula
for the
solution
of
(4.18):
exponentioally increasing (if yi > 0);
exponentioally decreasing (if yi < 0); or
constant (if yi = 0).
94
Chapter
4. Essential ordinary differential
equations
Since the basis
of
eigenvectors
{Ul,
U2,
U3}
of
A is orthonormal,
as
is easily checked,
we have
We can then immediately write down the solution to
It
is
dx
-=Ax,
dt
x(O)
=
xo.
If,
as in
the
previous example, A is symmetric,
then
the
eigenvectors
can
be
chosen
to
be
orthonormal,
in which case
it
is
particularly simple
to
compute
the
coefficient
Cl,
C2,
...
, C
n
expressing
Xo
in
terms
of
the
eigenvectors. We
obtain
the
following simple formula for
the
solution
of
(4.18):
n
x(t)
=
2)xo
.
ui)e"i(t-to)Ui.
i=l
We have derived
the
solution
to
(4.18) in
the
case
that
A
has
n linearly in-
dependent
eigenvectors. We
remark
that
formula (4.19) might involve complex
numbers
if
A
is
not
symmetric. However, we have a complete
and
satisfactory
solution in
the
case
that
A is
symmetric-there
are
n linearly independent eigen-
vectors,
the
eigenvalues are
guaranteed
to
be
real,
and
the
basis
of
eigenvectors
can
be
chosen
to
be
orthonormal.
We now discuss
the
significance
of
solution (4.19).
The
interpretation
is very
simple:
The
solution
to
(4.18) is
the
sum
of
n components, one in each eigendirec-
tion,
and
component
i
is
• exponentially increasing (if
Ai
> 0);
• exponentially decreasing (if
Ai
< 0);
or
•
constant
(if
Ai
= 0).

4.3. Linear
systems
with constant coefficients
95
Moreover,
the
rate
of
increase
or
decrease
of
each component
is
governed
by the
magnitude
of the
corresponding eigenvalue.
We
can
therefore draw
the
following conclusions:
The
only
statement
which requires justification
is the
third. Suppose
an
eigenvalue
\j of A is
positive,
and
suppose
A has k
linearly independent eigenvectors corre-
sponding
to \j.
Then, unless
XQ
lies
in the
(n
—
k)-dimensional
subspace
of
R
n
spanned
by the
other
n — k
eigenvectors,
the
solution
x of
(4.18)
will
contain
a
factor
of
e
Aj
(*~*°),
guaranteeing
the
||x(£)||
—>
oo as t
—>
oo.
Even
if k = 1, an (n — fc)-dimensional
subspace
of
R
n
is a
very small
part
of
R
n
(comparable
to a
plane
or a
line
in
R
3
). Therefore, most initial vectors
do not lie
in
this subspace.
Example 4.7.
Let
Then
the
eigenvalues
of
A are
AI
=
1,
A2
=
—1,
and
\s
=
—2,
and the
corresponding
eigenvectors
are
1. If all of the
eigenvalues
of A are
negative, then every solution
x of
(4.18)
satisfies
2.
If all of the
eigenvalues
of A are
positive, then every solution
x of
(4.18)
(except
the
zero solution) satisfies
3. If any of the
eigenvalues
of A is
positive, then,
for
most initial values
XQ,
the
solution
x of
(4.18) satisfies
where
The
solution
of
(4-18)
is
4.3. Linear systems with constant coefficients
95
Moreover,
the
rate
of increase or decrease of each component
is
governed by the
magnitude of
the
corresponding eigenvalue.
We
can therefore draw the following conclusions:
1.
If
all of the eigenvalues of A are negative, then every solution x of (4.18)
satisfies
Ilx(t)11
-t
0 as t
-t
00.
2.
If
all of the eigenvalues of A are positive, then every solution x of (4.18)
(except the zero solution) satisfies
Ilx(t)11
-t
00
as t
-t
00.
3.
If
any of the eigenvalues of A is positive, then, for most initial values xo, the
solution x of (4.18) satisfies
Ilx(t)11
-t
00
as t
-t
00.
The only statement which requires justification
is
the third. Suppose
an
eigenvalue
Aj of A is positive, and suppose A has k linearly independent eigenvectors corre-
sponding
to
Aj. Then, unless
Xo
lies in the (n - k )-dimensional subspace of R n
spanned by the other n - k eigenvectors, the solution x of (4.18) will contain a
factor of
eAj(t-t
O
),
guaranteeing the
Ilx(t)ll-t
00
as t
-t
00.
Even if k =
1,
an (n - k)-dimensional subspace of R
n
is
a very small
part
of Rn
(comparable
to
a plane or a line in R3). Therefore, most initial vectors do not lie
in this subspace.
Example
4.7.
Let
1
-1
1
Jl
Then
the eigenvalues
of
A are
Al
= 1,
A2
=
-1,
and
A3
=
-2,
and
the corresponding
eigenvectors are
The solution
of
(4.18) is
where

But S is a
plane,
which
is a
very
small part
of
Euclidean
3-space.
Thus
almost
every
initial
value
leads
to a
solution that
grows
exponentially.
Another
conclusion
that
we can
draw
is
somewhat more subtle
than
those
given
above,
but it
will
be
important
in
Chapter
6.
4. If A has
eigenvalues
of
very
different
magnitudes, then solutions
of
(4.18) have
components whose magnitudes change
at
very
different
rates.
Such solutions
can be
difficult
to
compute
efficiently
using numerical methods.
We
will
discuss this point
in
more detail
in
Section 4.5.
4.3.2
In
homogeneous
systems
and
variation
of
parameters
We
can now
explain
how to
solve
the
inhomogeneous system
96
Chapter
4.
Essential ordinary
differential
equations
The
only
initial
values
that
lead
to a
solution
x
that
does
not
grow
without
bound
are
again
only considering
the
case
in
which there
is a
basis
of
R
n
consisting
of
eigen-
vectors
of A. The
method
is a
spectral method,
and the
reader
may
wish
to
review
Section
3.5.3.
If
{ui,
u
2
,...,
u
n
}
is a
basis
for
R
n
,
then every vector
in
R
n
can be
written
uniquely
as a
linear combination
of
these vectors.
In
particular,
for
each
£,
we can
write
f(t)
as a
linear combination
of
ui,
112,...,
u
n
:
Of
course, since
the
vector
f
(t)
depends
on
£,
so do the
weights
c\
(£),
C2(t),...,
c
n
(t).
These weights
can be
computed explicitly
from
f,
which
of
course
is
considered
to
be
known.
We
can
also write
the
solution
of
(4.20)
in
terms
of the
basis vectors:
Since
x(£)
is
unknown,
so are the
weights
ai(i),«2(*),
• • •
,a,
n
(t).
However, when
these
basis
vectors
are
eigenvectors
of A, it is
easy
to
solve
for the
unknown weights.
Indeed, substituting (4.21)
in
place
of x
yields
96
Chapter
4.
Essential ordinary differential equations
The only initial values that lead to a solution x that
does
not grow without bound
are
Xo
E S = span{U2'
U3}.
But
S is a plane, which is a very small part
of
Euclidean 3-space. Thus almost
every initial value leads to a solution that grows exponentially.
Another conclusion
that
we
can draw
is
somewhat more subtle
than
those
given above,
but
it will be important in Chapter
6.
4.
If
A has eigenvalues of very different magnitudes, then solutions of (4.18) have
components whose magnitudes change
at
very different rates. Such solutions
can be difficult
to
compute efficiently using numerical methods.
We
will discuss this point in more detail in Section 4.5.
4.3.2 Inhomogeneous
systems
and
variation of parameters
We
can now explain how to solve the inhomogeneous system
dx
dt =
Ax
+ f(t),
(4.20)
again only considering the case in which there
is
a basis of Rn consisting of eigen-
vectors of
A.
The method
is
a spectral method,
and
the reader may wish
to
review
Section 3.5.3.
If
{Ul'
U2,
...
,
un}
is
a basis for R
n,
then every vector in R n can be written
uniquely as a linear combination of these vectors. In particular, for each
t,
we
can
write
f(t) as a linear combination of
Ul,
U2,
...
,
Un:
Of course, since the vector f(t) depends on t, so do
the
weights
Cl
(t), C2(t),
...
,en(t).
These weights can be computed explicitly from
f,
which of course
is
considered
to
be known.
We
can also write the solution of (4.20) in terms of
the
basis vectors:
(4.21)
Since
x(t)
is
unknown, so are
the
weights al(t),a2(t),
...
,a
n
(t). However, when
these basis vectors are eigenvectors of
A, it
is
easy
to
solve for the unknown weights.
Indeed, substituting (4.21) in place of x yields
dx
d[n
1
(n
)
--Ax=-
"'a·u-
-A
"'a-u-
dt
dt~"
~
••
i=l
i=l
n d n
= L
~Ui
-
LaiAui
i=l
dt
i=l

then implies
that
Example
4.8. Consider
the
IVP
16
This
is
just what happened
in the
spectral method
for
solving
Ax
=
b—the
system
of n
simultaneous
equations
was
reduced
to n
independent
equations.
4.3. Linear
systems
with
constant
coefficients
97
The ODE
which
can
only hold
if
When
the
basis
is
orthonormal,
the
coefficients
&i,&2j--->&n
can be
computed
in
the
usual way:
or
so
x(£
0
)
=
XQ
implies
that
We
will
concentrate
on
this case henceforth.
The
initial
condition
x(£
0
)
=
x
0
provides
initial
values
for the
unknowns
ai(t],a-2,(t},...
,a
n
(t}.
Indeed,
we can
write
Thus,
by
representing
the
solution
in
terms
of the
eigenvectors,
we
reduced
the
system
of
ODEs
to n
scalar ODEs
that
can be
solved
independently.
16
The
com-
putation
of the
functions
ci(£),
C2(t),...,
c
n
(t)
is
simplest when
A is
symmetric,
so
that
the
eigenvectors
can be
chosen
to be
orthonormal.
In
that
case,
4.3. Linear systems
with
constant coefficients
The ODE
then implies
that
which can only hold
if
dx
- -
Ax
= f(t)
dt
'"'
~
- A·a·
U·
=
'"'
c·(t)u·
n
{d
} n
L...J
dt
~
~ ~
L...J
~
~,
i=1
i=1
~i
_
Aiai
=
Ci(t),
i = 1,2,
...
,no
97
(4.22)
Thus, by representing
the
solution in terms of
the
eigenvectors,
we
reduced
the
system of ODEs
to
n scalar ODEs
that
can be solved independently.16 The com-
putation of
the
functions
C1
(t),
C2
(t),
...
, C
n
(t)
is
simplest when A is symmetric, so
that
the eigenvectors can be chosen
to
be orthonormal. In
that
case,
Ci(t)
= f(t) .
Ui,
i = 1,2,
...
,n.
We
will concentrate on this case henceforth.
The initial condition
x(to) =
Xo
provides initial values for the unknowns
a1
(t), a2(t),
...
, an(t). Indeed,
we
can write
so
x(to) =
Xo
implies
that
or
ai(to) = b
i
,
i = 1,2,
...
,no
When the basis
is
orthonormal, the coefficients b
1
,
b
2
,
.••
, b
n
can be computed in
the usual way:
b
i
=
Xo
.
Ui,
i = 1,2,
...
,n.
Example
4.8.
Consider the
IVP
dx
dt =
Ax
+ f(t),
x(O)
= 0,
16This is
just
what
happened
in
the
spectral
method
for solving
Ax
=
b-the
system
of
n
simultaneous equations was reduced
to
n
independent
equations.
