Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

158

Chapter

5.

Boundary value problems

in

statics

These

are

precisely

the

coefficients

of

UN'-

Therefore,

UN is the

best approximation

to

u

using

the first N

eigenfunctions.

The

last

example

is

typical:

By

solving

LDU

=

/N,

where

/AT

is the

best

ap-

proximation

to /

using

the first N

eigenfunctions,

we

obtain

the

best

approximation

UN

to the

solution

u of

LDU

=

/. We can

demonstrate

this

directly.

We

assume

that

u

satisfies

w(0)

=

u(C)

=

0, and we

write

ai,012,03,...

for the

Fourier (sine)

coefficients

of u:

(see

Exercise

5). We

begin

by

computing

the

Fourier sine

coefficients

of

f(x]

= x.

We

have

The

solution

to

L&U

—

/N,

with

is

then

We

can now

compare

UN

with

the

exact solution

u. In

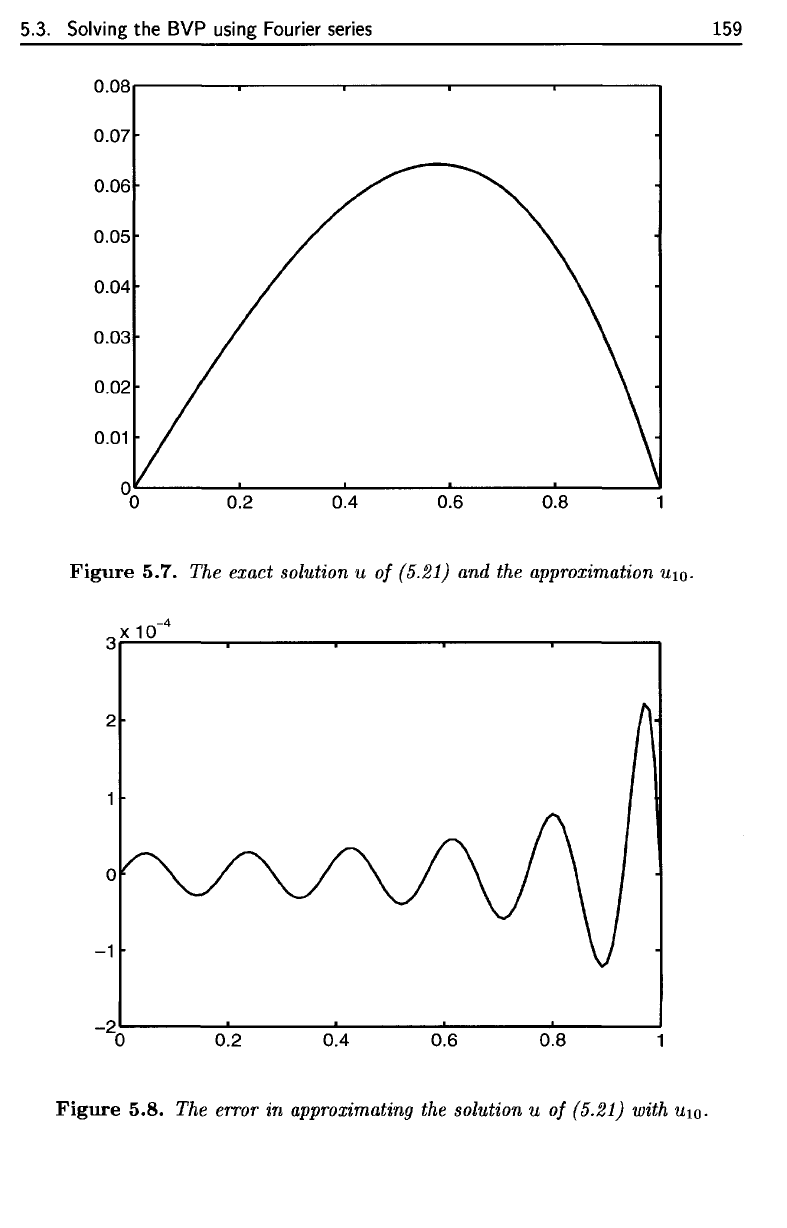
Figure 5.7,

we

show

the

graphs

of

u

anduw;

on

this scale,

the two

curves

are

indistinguishable. Figure

5.8

shows

the

approximation error

u(x)

—

UIQ(X).

The

fact that

UN

approximates

u so

closely

is no

accident.

If we

compute

the

Fourier sine

coefficients

ai,

02,

as,...

of

u

directly,

we find

that

We

can

then

compute

the

Fourier sine coefficients

of

by

using

integration

by

parts:

158 Chapter

5.

Boundary value problems

in

statics

(see Exercise 5). We

begin

by computing the Fourier sine coefficients

of

f(x)

=

x.

We have

1

1 . 2(_1)n+1

c

n

=2

xsm(n7fx)dx=

,

n=1,2,

....

o n7f

The solution to

LDu

=

fN,

with

N

fN(X) = L C

n

sin (mrx),

n=1

is then

N N 2(_1)n+1

UN(X) = L

~n

2 sin (n7fx) = L 3 3 sin (n7fx).

n=1

n

7f

n=1

n

7f

We can now compare

UN

with the exact solution

u.

In Figure 5.7,

we

show

the graphs

of

U and

UlOi

on this scale, the two curves

are

indistinguishable. Figure

5.8 shows the approximation error

u(x)

-

UlO(X).

The fact that

UN

approximates U

so

closely is no accident.

If

we compute the

Fourier sine coefficients

a1, a2, a3,

...

of

u directly, we find that

1

1 1

2.

2( _1)n+1

an = 2

-6x

(1-

x )

sm

(n7fx)

dx

= 3 3 ' n = 1,2,3,

....

o n

7f

These are precisely the coefficients

of

UN! Therefore,

UN

is the best approximation

to u using the first N eigenfunctions.

The

last

example is typical:

By

solving

LDU

=

fN,

where

fN

is

the

best

ap-

proximation

to

f using

the

first N eigenfunctions,

we

obtain

the

best

approximation

UN

to

the

solution u

of

LDU

=

f.

We

can demonstrate this directly.

We

assume

that

U satisfies

u(O)

=

u(f)

= 0,

and

we write

al,

a2, a3,

...

for

the

Fourier (sine)

coefficients

of

u:

an =

~

foi

u(x)

sin

(n;x)

dx, n = 1,2,3,

....

We

can

then

compute

the

Fourier sine coefficients of

by using integration by parts:

_T~U

dx

2

21£

d

2

u

(n7fx)

-

-T-(x)

sin -

dx

£ 0 dx

2

£

-2T{[dU

.

(n7fx)]l

n7f1ldU

(n7fx)}

=

--

-(x)sm

- - -

-(x)cos

-

dx

£

dx

£

",=0

£ 0

dx

£

-2T

{dU.

du.

n7f

t·

du

(n7fx)}

=

-£-

dx

(£)

sm (n7f) -

dx

(0)

sm

(0) - f

10

dx (x) cos

-£-

dx

5.3. Solving

the BVP

using Fourier

series

159

Figure 5.7.

The

exact

solution

u of

(5.21)

and the

approximation

UIQ.

Figure

5.8.

The

error

in

approximating

the

solution

u of

(5.21) with

UIQ.

5.3.

Solving

the

BVP

using

Fourier

series

159

O.OB.------r-----r------r-------r------..

0.07

Figure

5.7.

The exact solution u

of

{5.21} and the approximation

U10.

2

-2~---~----~---~----~---~

o 0.2 0.4 0.6

O.B

1

Figure

5.8.

The error in approximating the solution U

of

{5.21} with

U10'

160

Chapter

5.

Boundary value problems

in

statics

Example

5.12.

Consider

an

elastic

string that, when

stretched

by a

tension

of10

N,

has a

length

50 cm.

Suppose

that

the

density

of

the

(stretched)

string

is p = 0.2

g/

cm.

If

the

string

is fixed

horizontally

and

sags

under gravity,

what

shape

does

it

assume*

We

let

u(x),

0 < x < 50, be the

vertical

displacement

(in cm)

of

the

string.

To

use

consistent

units,

we

convert

10

Newtons

to

10

6

dynes

(gcm/s

2

).

Then

u

satisfies

the BVP

or

This

is

exactly what

we

obtained

by the

reasoning presented earlier.

or

Since

—Td?u/dx

2

= f by

assumption,

the

Fourier sine series

of the two

functions

must

be the

same,

and so we

obtain

is

We

thus

see

that

the

Fourier sine series

of

160

Chapter

5. Boundary value problems

in

statics

2Tmr r

i

du

(nnx)

. .

=

~

10

dx (x) cos

-e-

dx

(smce sm

(0)

= sin (nn) =

0)

(5.23)

=

2~~n

{ [u(x)

cos

(n;x)]

:=0

+

ne

n

fo£

u(x) sin

(n;x)

dX}

Tn

2

n

2

2 (

(nnx)

=

-e-

2

-g

10

u(x)

sin

-e-

dx

(since

u(O)

= u(e) =

0)

Tn

2

n

2

=~an'

We thus see

that

the

Fourier sine series of

is

_T~u

dx

2

Since

-Td

2

u/dx

2

= f by assumption,

the

Fourier sine series of

the

two functions

must be

the

same,

and

so

we

obtain

or

Tn

2

n

2

~an

= en, n =

1,2,3,

...

,

e

2

c

n

an =

-T

2

2'

n=

1,2,3,

....

nn

This is exactly

what

we

obtained by

the

reasoning presented earlier.

Example

5.12.

Consider an elastic string that, when stretched

by

a tension

of

10

N,

has a length

50

cm. Suppose that the density

of

the (stretched) string is p = 0.2

g/

cm.

If

the string is fixed horizontally and sags under gravity, what shape

does

it

assume?

We let

u(x),

0 < x < 50,

be

the vertical displacement (in cm)

of

the string.

To

use consistent units,

we

convert 10 Newtons

to

10

6

dynes

(g

cm/?).

Then u

satisfies the

BVP

~u

-T

dx

2

=

-pg,

0 < x <

e,

u(O)

= 0,

u(e) = 0,

or

6~U

-10

dx

2

=

-196,

0 < x < 50,

u(O)

= 0,

u(50) = 0

5.3. Solving

the BVP

using Fourier series

161

(using

980

cm/s

2

for

the

gravitational

constant).

To

solve

this,

we first

compute

the

Fourier

sine

coefficients

of the

right-hand side:

We

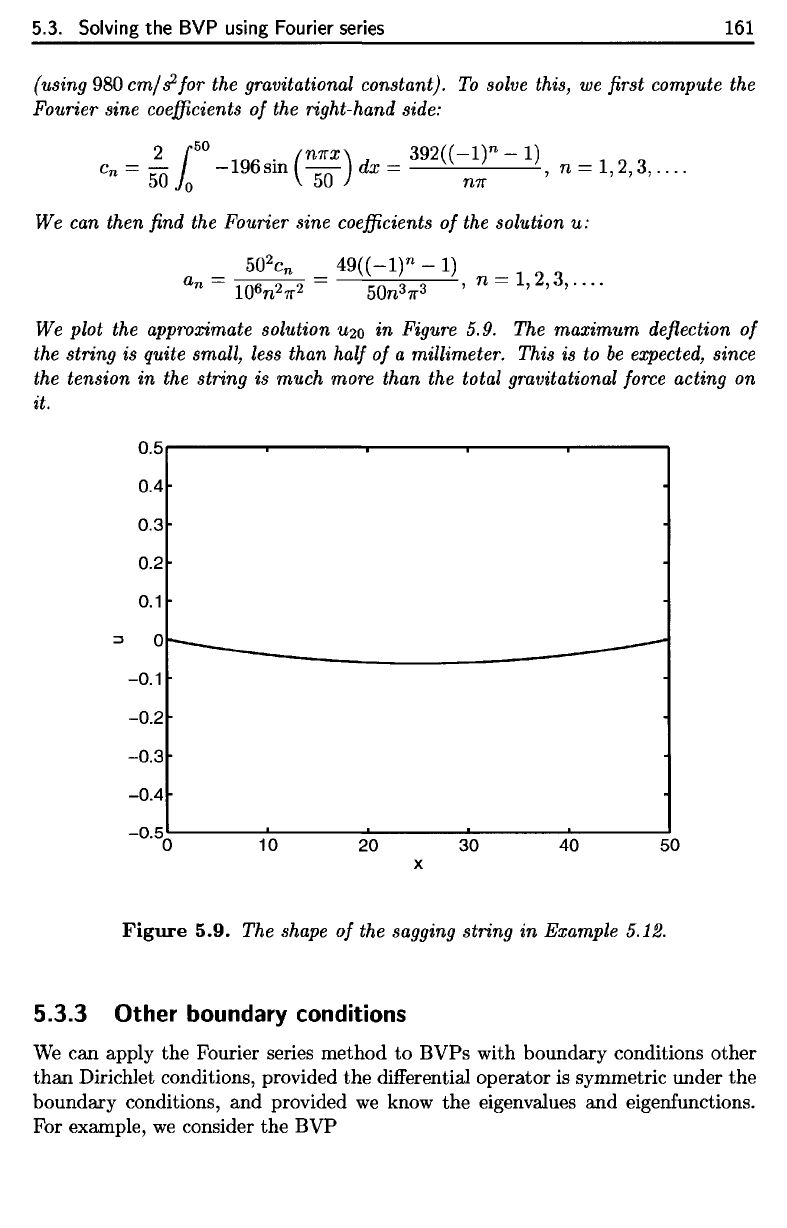
plot

the

approximate

solution

u^o

in

Figure 5.9.

The

maximum

deflection

of

the

string

is

quite small,

less

than

half

of a

millimeter. This

is to be

expected,

since

the

tension

in the

string

is

much more than

the

total gravitational

force

acting

on

it.

Figure

5.9.

The

shape

of the

sagging

string

in

Example 5.12.

5.3.3 Other boundary conditions

We

can

apply

the

Fourier series method

to

BVPs with boundary conditions other

than

Dirichlet

conditions,

provided

the

differential

operator

is

symmetric under

the

boundary conditions,

and

provided

we

know

the

eigenvalues

and

eigenfunctions.

For

example,

we

consider

the BVP

We

can

then

find the

Fourier sine

coefficients

of the

solution

u:

5.3. Solving the BVP using Fourier

series

161

(using 980

cm/

82

for the gravitational constant).

To

solve this, we first compute the

Fourier sine coefficients

of

the right-hand side:

21

50

.

(n1rx)

392((-1)n

-1)

C

n

= -

-196sm

--

dx

= , n =

1,2,3,

....

50 0 50

n1r

We can then find the Fourier sine coefficients

of

the solution

u:

50

2

c

n

49((

-l)n

-

1)

an = 10

6

2 2

= 3 3 ' n =

1,2,3,

....

n

1r

50n

1r

We plot the approximate solution

U20

in Figure

5.

g.

The

maximum

deflection

of

the string is quite small, less than half

of

a millimeter. This is to

be

expected, since

the tension in the string is much more than the total gravitational force acting on

it.

0.5

0.4

0.3

0.2

0.1

:::J

0

___

---

-0.1

-0.2

-0.3

-0.4

-0.5

0

10

20

30

40

50

x

Figure

5.9.

The shape

of

the sagging string in Example 5.12.

5.3.3 Other boundary

conditions

We

can apply

the

Fourier series method

to

BVPs with boundary conditions other

than

Dirichlet conditions, provided

the

differential operator is symmetric under

the

boundary conditions, and provided

we

know the eigenvalues and eigenfunctions.

For example,

we

consider the BVP

162

Chapter

5.

Boundary

value

problems

in

statics

The

fact

that

these

are the

correct Fourier

coefficients

can be

verified

by a

calculation

exactly like (5.23) (see Exercise

7) and is

also

justified

below

in

Section 5.3.5 (see

(5.29)).

The BVP

(5.24)

can now be

written

as

Written

as a

differential

operator equation, this takes

the

form

L

m

u

= /,

where

L

m

is

defined

as in

Section 5.2.3,

but

including

the

factor

of

T:

We

saw,

in

that

section,

that

the

eigenvalues

and

eigenfunctions

of

L

m

are

Therefore,

we

write

where

the

coefficients

01,02,03,...

are to be

determined.

The

Fourier series

of

L

m

u

=

—Td?u/dx

2

is

then

We

represent

the

solution

as

From

this

equation,

we see

that

162 Chapter

5.

Boundary value problems

in

statics

cPu

-T

dx2

=

I(x),

0 < x <

C,

u(O)

= 0,

(5.24)

du

(C)

=

O.

dx

Written as a differential operator equation, this takes the form Lmu =

I,

where

Lm

is

defined as in Section 5.2.3,

but

including

the

factor of T:

Lm

:

C;.

[0,

C]

-+

C[O,

CJ,

cPu

Lm

u

=

-T

dx

2

•

We

saw, in

that

section,

that

the eigenvalues

and

eigenfunctions of

Lm

are

T(2n-1)27r

2

.

((2n-1)7rx)

An

=

4C2

' ¢n(X) = sm

2f.

' n =

1,2,3,

....

Therefore,

we

write

I(

)

-

~

.

((2n

-

1)7rX)

x -

~cnsm

2f.

'

n=l

where

2 ( .

((2n-1)7rX)

Cn =

flo

I(x)

sm

2f.

dx, n =

1,2,3,

....

We

represent the solution as

~

.

((2n

-

1)7rX)

u(x)=~ansm

2£

'

where the coefficients

aI,

a2, a3,

.

..

are

to

be

determined.

The

Fourier series of

Lmu =

-TcPu/dx

2

is

then

_Td

2

u(

)_~T(2n-1)27r2

.

((2n-1)7rX)

dX2

x -

~

4C2

an

sm

2C

.

n=l

The

fact

that

these are the correct Fourier coefficients can be verified by a calculation

exactly like (5.23) (see Exercise

7)

and

is

also justified below in Section 5.3.5 (see

(5.29)).

The

BVP

(5.24) can now be written as

~

T(2n -

1)27r

2

.

((2n

-l)7rX)

_

~

.

((2n

-1)7rX)

~

4C2

an

sm

2C

-

~

en

sm

2f.

.

n=l n=l

From this equation,

we

see

that

5.3.

Solving

the BVP

using

Fourier

series

163

Thus

the

solution

to

(5.24)

is

We

then

have

Therefore,

the

solution

is

and the

eigenvalues

of the

differential

operator

are

or

Example

5.13. Consider

a

circular cylindrical bar,

of

length

1

m

and

radius

1

cm,

made from

an

aluminum

alloy with

stiffness

70 GPa and

density

2.64g/cm

3

.

Suppose

the top end of the bar (x =

Oj

is fixed and the

only force acting

on the bar

is the

force

due to

gravity.

We

will

find the

displacement

u

of

the bar and

determine

the

change

in

length

of

the bar

(which

is

just

u(\}).

The

BVP

describing

u is

where

k = 7 •

10

,

p —

2640

kg/m

3

,

and g = 9.8

m/s

2

.

The

Fourier quarter-wave

sine

coefficients

of the

constant

function

pg are

5.3. Solving the BVP using Fourier series 163

or

4£2C

n

an

=

T(2n

_

1)27f2

, n =

1,2,3,

....

Thus the solution

to

(5.24)

is

~

4£2C

n .

((2n-1)7fX)

u(x)

=

~

T(2n

_

1)27f2

sm

2£

.

Example

5.13.

Consider a circular cylindrical

bar,

of

length 1 m and radius 1

cm, made from an aluminum alloy with stiffness

70

CPa and density 2.64

gj

cm

3

.

Suppose the top end

of

the

bar

(x = 0) is fixed and the only force acting on the

bar

is the force due to gravity. We will find the displacement u

of

the

bar

and determine

the change

in

length

of

the

bar

(which is

just

u(l)).

The B

VP

describing u is

~u

-k

dx

2

=

pg,

0 < x < 1,

u(O)

= 0,

(5.25)

~~(1)=0,

where k = 7 .

1010,

P = 2640 kgj m

3

,

and 9 = 9.8

mj

~

. The Fourier quarter-wave

sine coefficients

of

the constant function

pg

are

1

1 .

((2n

- l)7rX)

4pg

C

n

= 2 0

pg

sm

2

dx

= (2n _ 1)7f' n =

1,2,3,

...

,

and the eigenvalues

of

the differential operator

are

k(2n

-

1)27f2

4 ' n =

1,2,3,

....

Therefore, the solution is

()

L

oo

16pg

.

((2n

- l)7fX)

ux

=

SIn

n=1

k(2n -

1)37f3

2

.

-6

~

1 .

((2n

-l)7fX)

= (5.9136· 10 )

~

(2n _

1)37f3

sm

2 .

We then have

. (

-6)

~

1 .

((2n

- 1)7f)

u(l)

= 5.9136· 10

~

(2n _

1)37f3

sm

2

-6

00

(_l)n+I

=

(5.9136·10

)

~

(2n _

1)37r3

~

1.85 .

10-

7

.

164

Chapter

5.

Boundary

value

problems

in

statics

Thus

the bar

stretches

by

only

about

1.85

•

10~

7

m,

or

less

than

two

ten-thousandths

of

a

millimeter.

The

Fourier series method

is a

fairly

complicated technique

for

solving such

a

simple problem

as

(5.13).

As we

mentioned

in

Section

5.1.1,

we

could simply

integrate

the

differential

equation twice

and use the

boundary conditions

to

deter-

mine

the

constants

of

integration.

The

Fourier series method

will

prove

its

worth

when

we

apply

it to

PDEs,

either time-dependent problems (Chapters

6 and 7) or

problems with multiple

spatial

dimensions (Chapter

8). We

introduce

the

Fourier

series method

in

this simple context

so

that

the

reader

can

understand

its

essence

before

dealing with more complicated applications.

satisfies

the

boundary conditions

(p(0)

=

a,

p(t)

= b). If we

define

v(x)

=

u(x)

—

#(V),

then

since

the

second derivative

of a

linear

function

is

zero.

Also,

Thus v(x) solves (5.10),

so we

know

how to

compute v(x).

We

then have

u(x)

=

v(x]

+p(x).

This

technique,

of

transforming

the

problem

to one

with homogeneous bound-

ary

conditions,

is

referred

to as the

method

of

shifting

the

data.

Example

5.14.

Consider

5.3.4

In

homogeneous

boundary

conditions

We

now

consider

the

following

BVP

with inhomogeneous boundary conditions:

(T

constant).

To

apply

the

Fourier series method

to

this problem,

we

make

a

transformation

of the

dependent variable

u

to

obtain

a BVP

with homogeneous

boundary conditions.

We

notice

that

the

linear

function

164

Chapter

5.

Boundary value problems

in

statics

Thus the

bar

stretches

by

only about 1.85·

10-

7

m,

or

less

than two ten-thousandths

01

a millimeter.

The Fourier series method is a fairly complicated technique for solving such

a simple problem as (5.13). As

we

mentioned in Section 5.1.1,

we

could simply

integrate

the

differential equation twice and use the boundary conditions

to

deter-

mine

the

constants of integration. The Fourier series method will prove its worth

when

we

apply

it

to

PDEs, either time-dependent problems (Chapters 6

and

7)

or

problems with multiple spatial dimensions (Chapter 8).

We

introduce

the

Fourier

series method in this simple context so

that

the reader can understand its essence

before dealing with more complicated applications.

5.3.4 Inhomogeneous boundary conditions

We

now consider the following BVP with inhomogeneous boundary conditions:

d?u

-T

d,x2 =

I(x),

0 < x <

e,

u(O)

=

a,

(5.26)

u(e)

= b

(T

constant). To apply the Fourier series method

to

this problem,

we

make a

transformation of the dependent variable

u

to

obtain a BVP with homogeneous

boundary conditions.

We

notice

that

the

linear function

b-a

p(x) = a +

-e-x

satisfies

the

boundary conditions

(P(O)

= a,

pee)

=

b).

If

we

define

vex)

= u(x) -

p(x),

then

d?v

d?u

d

2

p

-T

dx

2

=

-T

d,x2 + T d,x2 =

I(x)

+ 0 =

I(x),

since the second derivative of a linear function

is

zero. Also,

v(O)

=

u(O)

-

p(O)

= a - a =

0,

vee)

=

u(e)

-

pee)

= b - b =

O.

Thus

vex)

solves (5.10),

so

we

know how to compute

vex).

We

then have u(x) =

vex)

+ p(x).

This technique, of transforming

the

problem

to

one with homogeneous bound-

ary conditions,

is

referred

to

as

the

method of shifting the

data.

Example

5.14.

Consider

d?u

-

dx

2

= x, 0 < x < 1,

u(O)

=

1,

(5.27)

u(l)

=

O.

5.3.

Solving

the BVP

using

Fourier

series

165

Let

p(x]

=

I

—

x, the

linear function

satisfying

the

boundary conditions,

and

define

v(x)

—

u(x]

—p(x).

Then v(x) solves (5.21),

and so

We

then

have

Example

5.15. Consider again

the bar of

Example 5.13,

and

suppose that

now a

mass

of

1000

kg is

hung from

the

bottom

end of the

bar.

Assume

that

the

mass

is

evenly

distributed over

the end of the

bar, resulting

in a

pressure

of

on the end of the

bar.

The BVP

satisfied

by the

displacement

u is now

where

k — 7 •

10

,

p =

2640

kg/m

3

,

and g = 9.8

m/s

2

.

To

solve this problem using

the

Fourier series

method,

we

shift

the

data

by finding a

linear function

satisfying

the

boundary conditions.

The

function

satisfies

so

we

define

v = u

—

q. It

then

turns

out

that,

since

d

q/dx

= 0,

that

v

satisfies

(5.25),

so

We

then

obtain

and

This

is 1.4

millimeters.

The

displacement

due to

gravity

("1.85

• 10

millimeters)

is

insignificant compared

to the

displacement

due to the

mass hanging

on the end of

the

bar.

5.3. Solving the BVP using Fourier

series

165

Let

p(x)

= 1 -

x,

the linear function satisfying the boundary conditions, and define

vex)

=

u(x)

-

p(x).

Then

v(x)

solves

{5.21},

and

so

00

2(

_l)n+l

v(x)

= L 3 3 sin (ml'x).

n7r

n=l

We then have

00

2(_1)n+l

u(x)

=

1-

x+

L 3 3 sin (n7rx).

n7r

n=l

Example

5.15.

Consider again the bar

of

Example 5.13, and suppose that now a

mass

of

1000

kg

is hung from the bottom end

of

the

bar.

Assume

that the mass is

evenly distributed over the end

of

the

bar,

resulting

in

a pressure

of

_ (1000kg)

(9.8mj

?)

_

9.8·

10

7

Pa

p -

7r

(10-

2

)2

m

2

-

7r

on the end

of

the

bar.

The

BVP

satisfied by the displacement u is now

d

2

u

- k

dx

2

= pg, 0 < x < 1,

u(O)

=

0,

(5.28)

dU(l) = E

dx

k'

where k =

7·

lO

lD

,

P = 2640 kgj m

3

,

and g = 9.8

mj?

To

solve this problem using

the Fourier series method,

we

shift the data

by

finding a linear function satisfying

the boundary conditions. The function

q(x)

=

tx

satisfies

dq

p

q(O)

= 0,

dx

(1) = 'k'

so

we

define v = u - q.

It

then turns out that, since

~qjdx2

= 0, that v satisfies

{5.25},

so

vex)

~

(5.9136.10-

6

)

f (

1)3

3 sin

((2n

-l)7rX)

2n - 1

7r

2

n=l

and

. P

-6

~

1 .

((2n

- 1)7rX)

u(x)

=

'kx

+

(5.9136·10

)

~

(2n _

1)37r

3

sm

2 .

We then obtain

u(1)

~

t + 1.8

.10-

7

~

1.4

.10-

3

•

This is 1.4 millimeters. The displacement due to gravity {1.85·

10-

4

millimeters}

is insignificant compared to the displacement due to the mass hanging on the end

of

the

bar.

166

Chapter

5.

Boundary

value

problems

in

statics

5.3.5 Summary

We

can now

summarize

the

method

of

Fourier series

for

solving

a

BVP.

We

assume

that

the BVP has

been written

in the

form

Ku

—

/,

where,

as

usual,

the

boundary

conditions

form

part

of the

definition

of the

domain

of the

differential

operator

K.

For

the

Fourier series method

to be

applicable,

it

must

be the

case

that

K is

symmetric;

K has a

sequence

of

eigenvalues

AI,

A2,

AS,

...,

with corresponding

eigenfunc-

tions

Vi?

V%

V'S)

• • •

(which

are

necessarily

orthogonal);

any

function

g in

(7[0,

f]

can be

written

in a

Fourier series

where

It

then

follows

that

the

function

Ku is

given

by the

series

where

ai,

02,03,...

are the

Fourier

coefficients

of

u.

This

follows

from

the

symmetry

of

K and the

definition

of the

Fourier

coefficients

&i,

62,63,...

of Ku:

The BVP Ku = f

then

takes

the

form

whence

we

obtain

166 Chapter 5. Boundary value problems

in

statics

5.3.5 Summary

We

can now summarize the method of Fourier series for solving a BVP.

We

assume

that

the

BVP has been written in

the

form K u = f, where, as usual, the boundary

conditions form

part

of the definition of the domain of the differential operator

K.

For the Fourier series method

to

be applicable, it must be the case

that

• K is symmetric;

• K has a sequence of eigenvalues

A1,

A2,

A3,

...

, with corresponding eigenfunc-

tions

'¢1,

1/J2, 1/J3,

...

(which are necessarily orthogonal);

• any function

9 in

e[O,

£]

can be written in a Fourier series

00

g(x) = L d

n

1/Jn(x)

,

n=l

where

It

then follows

that

the

function K u

is

given by

the

series

00

(Ku)(x) = L

An

a

n1/Jn(X)

,

n=l

where al,

a2,

a3,'" are the Fourier coefficients of

u.

This follows from the symmetry

of

K and

the

definition of the Fourier coefficients b

l

,

b

2

,

b

3

,

..•

of K

u:

b

n

=

(K

u,

1/Jn)

(1/Jn,'¢n)

(u,

K1/Jn)

=-'c--'_--'--'-'':-

(1/Jn,

1/Jn)

(u,

An1/Jn)

(1/Jn,1/Jn)

=

An

(u,

1/Jn)

(1/Jn,1/Jn)

=

Anan·

The BVP K u = f then takes

the

form

00

L

An

a

n1/Jn(X)

= L c

n

1/Jn(x),

n=l

whence

we

obtain

C

n

an

= An' n =

1,2,3,

...

,

(5.29)

5.3.

Solving

the BVP

using Fourier

series

167

when

k(x)

is

nonconstant,

it is

more

work

to find the

eigenfunctions

than

to

just

solve

the

problem using

a

different

method.

For

this reason,

we

discuss

a

more

broadly applicable method,

the finite

element method, beginning

in

Section 5.4.

and

Here

is a

summary

of the

Fourier series method

for

solving BVPs.

0.

Pose

the BVP as a

differential

operator equation.

1.

Verify

that

the

operator

is

symmetric,

and find the

eigenvalue/eigenfunction

pairs.

2.

Express

the

unknown

function

u as a

series

in

terms

of the

eigenfunctions.

The

coefficients

are the

unknowns

of the

problem.

3.

Express

the

right-hand side

/ of the

differential

equation

as a

series

in

terms

of

the

eigenfunctions.

Use the

formula

for the

projection

of /

onto

the

eigen-

functions

to

compute

the

coefficients.

4.

Express

the

left-hand side

of the

differential

equation

in a

series

in

terms

of

the

eigenfunctions. This

is

done

by

simply multiplying

the

Fourier

coefficients

of

u by the

corresponding eigenvalues.

5.

Equate

the

coefficients

in the

series

for the

left-

and

right-hand sides

of the

differential

equation,

and

solve

for the

unknowns.

As

mentioned above,

the

Fourier series method

is

analogous

to

what

we

called

(in

Section 3.5)

the

spectral method

for

solving

Ax = b.

This method

is

only

applicable

if the

matrix

A is

symmetric,

so

that

the

eigenvectors

are

orthogonal.

In

the

same way,

the

method described above

fails

at the first

step

if the

eigenfunctions

are not

orthogonal,

that

is, if the

differential

operator

is not

symmetric.

An

even more pertinent observation

is

that

one

rarely uses

the

spectral method

to

solve

Ax = 6, for the

simple reason

that

computing

the

eigenpairs

of A is

more

costly,

in

most cases, than solving

Ax = b

directly

by

other means.

It is

only

in

special cases

that

one

knows

the

eigenpairs

of a

matrix.

In the

same way,

it is

only

for

very

special

differential

operators

that

the

eigenvalues

and

eigenfunctions

can be

found.

Therefore,

the

method

of

Fourier series, which works very

well

when

it can

be

used,

is

applicable

to

only

a

small

set of

problems.

On

most problems, such

as

the BVP

5.3. Solving the BVP using Fourier

series

167

and

00

u(x) =

2:

~:

1Pn(x).

n=l

Here is a summary of

the

Fourier series method for solving BVPs.

O.

Pose

the

BVP

a.s

a differential operator equation.

1.

Verify

that

the

operator is symmetric,

and

find

the

eigenvalue/eigenfunction

pairs.

2.

Express

the

unknown function u as a series in terms of

the

eigenfunctions.

The

coefficients are

the

unknowns of

the

problem.

3. Express

the

right-hand side f of

the

differential equation

a.s

a series in terms

of

the

eigenfunctions. Use the formula for

the

projection of f onto

the

eigen-

functions

to

compute the coefficients.

4. Express

the

left-hand side of the differential equation in a series in terms of

the

eigenfunctions. This

is

done by simply multiplying

the

Fourier coefficients

of

u by

the

corresponding eigenvalues.

5.

Equate

the

coefficients in

the

series for

the

left- and right-hand sides of the

differential equation,

and

solve for

the

unknowns.

As

mentioned above,

the

Fourier series method

is

analogous

to

what

we

called

(in Section 3.5)

the

spectral method for solving

Ax

=

b.

This method is only

applicable if the matrix A is symmetric, so

that

the

eigenvectors are orthogonal. In

the

same way,

the

method described above fails

at

the

first step if

the

eigenfunctions

are not orthogonal,

that

is, if

the

differential operator is

not

symmetric.

An even more pertinent observation is

that

one rarely uses

the

spectral method

to

solve

Ax

=

b,

for

the

simple reason

that

computing

the

eigenpairs of A is more

costly, in most cases,

than

solving

Ax

= b directly by

other

means.

It

is only in

special cases

that

one knows

the

eigenpairs of a matrix. In

the

same way,

it

is only

for very special differential operators that the eigenvalues and eigenfunctions can

be

found. Therefore,

the

method of Fourier series, which works very well when

it

can

be used, is applicable

to

only a small set of problems. On most problems, such as

the

BVP

d (

dU)

-

dx

k(x)

dx

=

f(x),

0 < x <

£,

u(O)

= 0,

u(£)

= 0

when k(x) is nonconstant,

it

is

more work

to

find

the

eigenfunctions

than

to

just

solve

the

problem using a different method. For this reason,

we

discuss a more

broadly applicable method,

the

finite element method, beginning in Section 5.4.

Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

Подождите немного. Документ загружается.