Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

we

see

that

We

now

take,

for

example,

v(x)

=

I

—

x/l,

which certainly belongs

to

V.

With this

choice

of

v,

(6.47)

becomes

268

Chapter

6.

Heat flow

and

diffusion

Now,

V C

V,

where

V is

defined

as the

space

of

test

functions

used

for a

Dirichlet

problem:

Therefore,

in

particular, (6.46) holds

for all v

e

V.

Since

the

boundary term

in

(6.46)

vanishes when

v(0)

=

v(t}

= 0, we

obtain

or

Using

the

same argument

as in

Section 5.4.2,

we see

that

must hold,

or

equivalently,

that

Thus,

if u

satisfies

the

weak

form

of the

BVP,

it

must

satisfy

at

least

the

differential

equation appearing

in the

strong

form.

It is now

easy

to

show

that

the

boundary conditions also hold.

The

condition

(6.46)

is

equivalent

to

and, since

we

have already shown

that

(since

v(0)

= 1,

v(i)

= 0).

Since

fc(0) > 0 by

assumption, this

can

hold only

if

268

Chapter

6.

Heat flow

and

diffusion

Now, V C

V,

where V

is

defined as

the

space of test functions used for a Dirichlet

problem:

V =

c1[0,

R]

=

{v

E V :

v(O)

=

v(R)

=

O}

.

Therefore, in particular, (6.46) holds for all v E V. Since the boundary term in

(6.46) vanishes when

v(O)

=

v(R)

= 0,

we

obtain

i

f d [ dU]

if

- 0

dx

k(x)

dx

(x)

vex)

dx

= 0

f(x)v(x)

dx

for all v E

V,

or

fat

{!

[k(X)

:~

(x)] +

f(X)}

vex)

dx

= 0 for all v E

V.

Using the same argument as in Section 5.4.2,

we

see

that

d [

du

]

dx

k(x)dx(x)

+f(x)

=0,

O<x<R

must hold, or equivalently,

that

d [

du

]

-

dx

k(x)

dx

(x) =

f(x),

0 < x <

£.

Thus, if U satisfies the weak form

of

the

BVP,

it

must satisfy

at

least

the

differential

equation appearing in the strong form.

It

is now easy

to

show

that

the boundary conditions also hold.

The

condition

(6.46)

is

equivalent

to

[

du

] i

rt

{ d [

dU]}

_

- k(x)

dx

(x)v(x) 0 +

10

dx

k(x)

dx

(x)

+

f(x)

vex)

dx

= 0 for all v E

V,

and, since

we

have already shown

that

d [

du

]

dx

k(x)

dx

(x)

+f(x)

=0,

O<x<R,

we

see

that

[

du

] i _

k(x)

dx

(x)v(x) 0 = 0 for all v E V.

(6.47)

We

now take, for example,

vex)

=

1-

x/R,

which certainly belongs to

V.

With

this

choice of

v, (6.47) becomes

-k(O):

(0)

= 0

(since

v(O)

=

1,

v(R)

= 0). Since

k(O)

> 0 by assumption, this can hold only if

du

dx

(0)

=

O.

6.5.

Finite

elements

and

Neumann conditions

269

must hold. Thus, when

u

satisfies

the

weak

form

(6.45),

it

must necessarily

satisfy

the

Neumann boundary conditions. This completes

the

proof

that

the

strong

and

weak

forms

of BVP

(6.44)

are

equivalent.

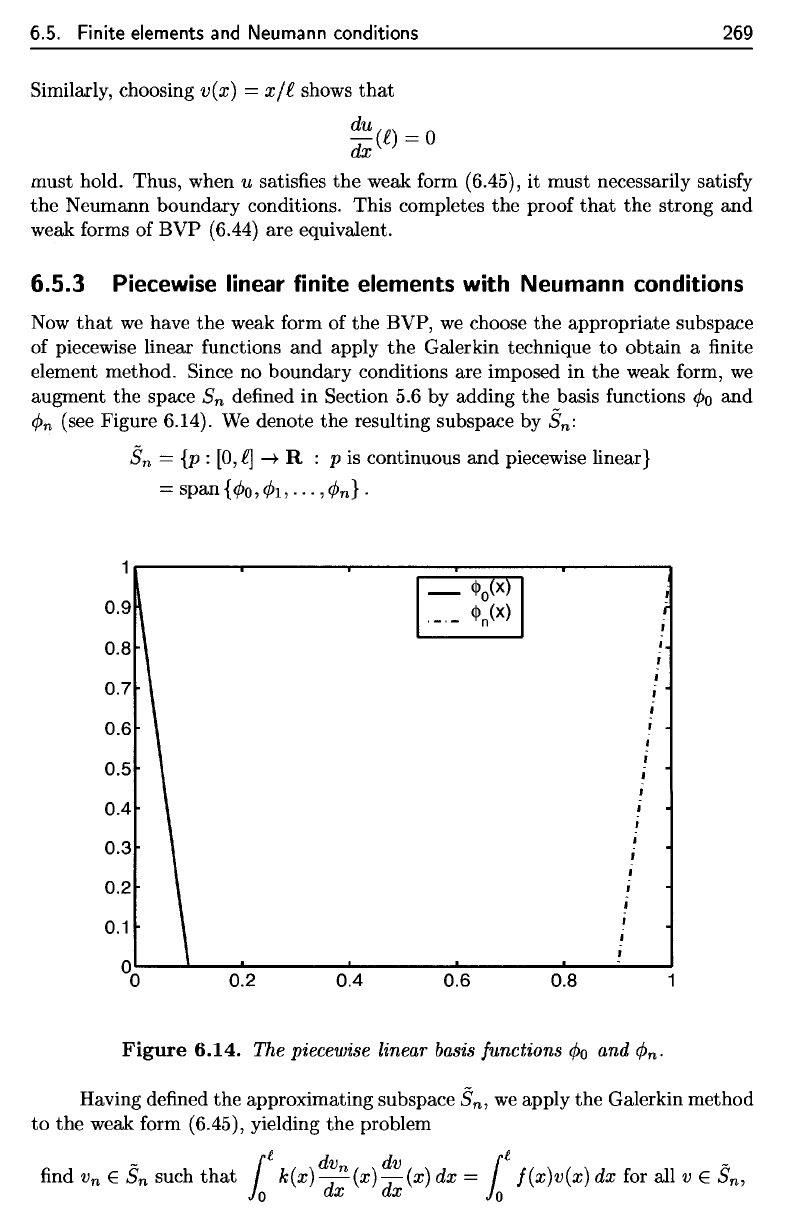
Figure

6.14.

The

piecewise

linear

basis

functions

</>o

and

(f)

n

.

Having

defined

the

approximating subspace

5

n

,

we

apply

the

Galerkin method

to the

weak

form

(6.45), yielding

the

problem

Similarly,

choosing

v(x)

=

x/i

shows

that

6.5.3

Piecewise

linear

finite

elements

with

Neumann

conditions

Now

that

we

have

the

weak

form

of the

BVP,

we

choose

the

appropriate subspace

of

piecewise linear

functions

and

apply

the

Galerkin technique

to

obtain

a finite

element

method. Since

no

boundary conditions

are

imposed

in the

weak

form,

we

augment

the

space

S

n

defined

in

Section

5.6 by

adding

the

basis

functions

</>o

and

0

n

(see Figure 6.14).

We

denote

the

resulting subspace

by

S

n

:

Sn — {p

'•

[Oj^j

—*•

R-

:

P is

continuous

and

piecewise

linear}

=

span{</>o,0i,...,0

n

}.

6.5. Finite elements

and

Neumann conditions

Similarly, choosing v(x) =

xli

shows

that

du

(i)

= 0

dx

269

must hold. Thus, when u satisfies

the

weak form (6.45),

it

must necessarily satisfy

the

Neumann boundary conditions. This completes

the

proof

that

the strong and

weak forms of

BVP

(6.44) are equivalent.

6.5.3 Piecewise linear finite elements with Neumann conditions

Now

that

we

have

the

weak form of the BVP,

we

choose

the

appropriate subspace

of piecewise linear functions and apply

the

Galerkin technique

to

obtain a finite

element method. Since no boundary conditions are imposed in

the

weak form,

we

augment the space Sn defined in Section 5.6 by adding

the

basis functions

4>0

and

4>n

(see Figure 6.14).

We

denote the resulting subspace by

Sn:

Sn = {p :

[0,

i]

-+

R : p

is

continuous and piecewise linear}

= span {

4>0,

4>1,

...

,

4>n}

.

0.9

~

._._

<pn(x)

0.8

0.7

\

0.6

0.5

,

i

0.4

,

0.3

0.2

0.1

\

,

00

0.2 0.4 0.6 0.8

,

j

!

,

Figure

6.14.

The piecewise linear

basis

functions

4>0

and

4>n.

Having defined

the

approximating subspace Sn,

we

apply the Galerkin method

to

the

weak form (6.45), yielding the problem

- r

l

dV

n

dv

r

l

-

find

Vn

E Sn such

that

10

k(x) dx (x) dx (x) dx =

10

f(x)v(x)

dx for all v E Sn,

270

Chapter

6.

Heat flow

and

diffusion

or,

equivalently,

For

simplicity

of

notation,

we

will

again write

so

that

(6.48)

can be

written

as

We

then write

the

unknown

v

n

as

and

substitute into (6.49).

The

result

is

This

is a

system

of

n

+ 1

equations

in the

n

+

I

unknowns

uo,ui,...,u

n

.

We can

write

the

system

as the

matrix-vector equation

Kii

= f by

defining

The

calculations involved

in

forming

the

matrix

K and the

vector

f are

exactly

the

same

as for a

Dirichlet problem, except

that

0

and

4>

n

are

qualitatively

different

from

0i,

02,...,

0n-i

(0o

and

0

n

are

each nonzero

on a

single subinterval, namely

[XQ,

Xi]

and

[x

n

_i,

x

n

],

respectively, while each

0j,

i =

1,2,...,

n

—

1, is

nonzero

on

[Xi-i,X

i+

i}}.

Having

now

reduced

the

problem

to the

linear system

Kii =

f,

where

now

K

6

R(n+i)x(n+i)

and

^

f

e

R

n+i

5

we

face

the

Difficulty

that

K is a

singular

matrix.

This

is not

surprising, since

we

know

that

the

original

BVP

(6.44) does

not

have

a

unique solution.

We can

show directly

that

K is

singular,

and

understand

the

nature

of the

singularity,

as

follows.

If

270

Chapter

6.

Heat flow

and

diffusion

or, equivalently,

find

Vn

E Sn such

that

lot

k(x)

~;

(x)

dx

i

(x) dx

=

10£

!(X)tPi(X) dx, i =

0,1,

...

, n.

(6.48)

For simplicity of notation,

we

will again write

(t

dv

dw

a(v,

w)

= io k(x) dx (x) dx (x) dx,

so

that

(6.48) can be written as

We

then

write

the

unknown

Vn

as

n

Vn

=

LUjtPj

j=O

and

substitute into (6.49).

The

result

is

n

La(tPj,tPi)Uj = (J,tPi), i

=O,l,

...

,n.

i=O

(6.49)

This is a system of

n + 1 equations in

the

n + 1 unknowns

uo,

UI,

...

,

Un.

We

can

write

the

system as

the

matrix-vector equation

Kii

= f by defining

Kij =

a(tPj,

tPi),

i,j

=

0,1,

...

, n,

ii

= (J,tPi)' i =

O,l,

...

,n.

The

calculations involved in forming

the

matrix

K

and

the

vector f are exactly

the

same as for a Dirichlet problem, except

that

tPo

and

tPn

are qualitatively different

from

tPI,

tP2,

...

,

tPn-1

(tPo

and

tPn

are each nonzero on a single subinterval, namely

[xo,

Xl]

and

[Xn-l,

xn],

respectively, while each

tPi,

i = 1,2,

...

, n -

1,

is nonzero on

[Xi-I,

Xi+l]).

Having now reduced

the

problem

to

the

linear system

Kii

=

f,

where now

K E

R(n+1)x

(n+1)

and

ii, f E

Rn+1,

we

face

the

difficulty

that

K is a singular

matrix. This

is

not

surprising, since

we

know

that

the original

BVP

(6.44) does not

have a unique solution.

We

can show directly

that

K is singular, and understand

the

nature

of

the

singularity, as follows.

If

6.5.

Finite

elements

and

Neumann

conditions

271

then

is

piecewise linear

and has

value

one at

each mesh node.

It

follows

that

(6.50)

is

the

constant

function

one,

and

hence

has

derivative zero. Therefore

(Ku

c

)j

= 0 for

each

ij

which shows

that

Ku

c

= 0 and

hence

that

K is

singular. Moreover,

it can

be

shown

that

u

c

spans

the

null space

of K;

that

is, if

Ku

= 0,

then

u

is a

multiple

of

u

c

(see Exercise

5].

The

fact

that

K is

singular means

that

we

must give special

attention

to the

process

of

solving

Ku = f. In

particular,

if we

ignore

the

singularity

of K and

solve

Kii = f

using computer software,

we

will

get

either

a

meaningless solution

or

an

error message.

To

solve this singular system correctly,

we

must

add

another

equation (one additional equation, correctly chosen,

will

be

sufficient,

because

the

null

space

of K is

one-dimensional).

A

simple choice

is the

equation

u

n

= 0;

this

is

equivalent

to

choosing,

out of the

infinitely

many solutions

to

(6.44),

the one

with

u(i]

— 0.

Moreover,

we can

impose this additional equation

by

simply removing

the

last

row and

column

from

K, and the

last

entry

from

f.

The

last

column

of K

consists

of the

coefficients

of the

terms

in the

equations involving

u

n

;

if we

insist

that

u

n

= 0,

then

we can

remove these terms

from

all n + 1

equations.

We

then

have

n

+

l

equations

in the n

unknowns

WQ,

Wi,...,

w

n

_i.

This

is one

more equation

than

we

need,

so we

remove

one

equation,

the

last,

to

obtain

a

square system.

It

can be

proved

that

the

resulting

n x n

system

is

nonsingular (see Exercise

11).

Of

course,

we

could have removed

a

different

row and

column.

If we

remove

the

iih

row and

column,

we are

selecting

the

approximate solution

v

n

satisfying

V

n

(Xi)

= 0.

Example

6.10. Consider

the

Neumann problem

It is

easy

to

show

(by

direct

integration) that

But

6.5. Finite elements

and

Neumann conditions 271

then

But

(6.50)

j=O

is piecewise linear and has value one

at

each mesh node.

It

follows

that

(6.50)

is

the

constant function one, and hence has derivative zero. Therefore

CKUe)i

= 0 for

each

i,

which shows

that

KU

e

= 0 and hence

that

K

is

singular. Moreover,

it

can

be shown

that

U

e

spans

the

null space of

K;

that

is, if

Kii

=

0,

then

ii

is

a multiple

of

U

e

(see Exercise

5}

The

fact

that

K

is

singular means

that

we

must give special attention to the

process of solving

Kii

=

f.

In particular, if

we

ignore the singularity of K and

solve

Kii

= f using computer software,

we

will get either a meaningless solution

or

an

error message. To solve this singular system correctly,

we

must add another

equation (one additional equation, correctly chosen, will be sufficient, because the

null space of

K

is

one-dimensional). A simple choice

is

the equation

Un

=

0;

this

is

equivalent

to

choosing, out of

the

infinitely many solutions

to

(6.44), the one with

u(C)

=

O.

Moreover,

we

can

i~pose

this additional equation by simply removing;

the last row and column from

K,

and the last entry from

f.

The last column of K

consists of

the

coefficients of the terms in

the

equations involving

un;

if

we

insist

that

Un

= 0,

then

we

can remove these terms from all n + 1 equations.

We

then

have

n + 1 equations in the n unknowns

uo,

ut,

... ,

Un-l.

This

is

one more equation

than

we

need,

so

we

remove one equation, the last,

to

obtain a square system.

It

can be proved

that

the resulting n x n system

is

nonsingular (see Exercise 11).

Of course,

we

could have removed a different row and column.

If

we

remove

the

ith

row and column,

we

are selecting the approximate solution

Vn

satisfying

Vn(Xi)

=

O.

Example

6.10.

Consider the Neumann problem

d

2

u 1

--

= x - - 0 < x < 1

dX2

2'

,

~:

(0)

=

0,

(6.51 )

~:

(1) = 0.

It

is

easy

to

show (by direct integration) that

X3 X2

u(x) =

-"6

+

4"

+ C

272

Chapter

6.

Heat flow

and

diffusion

is

a

solution

for any

constant

C,

and

that

is

the

solution

satisfying

u(l)

= 0.

We

will

use a

regular grid with

the finite

element method.

We

define

xi

= ih,

i =

0,1,...,n,

h —

l/n.

With piecewise linear

finite

elements,

as we

have seen

before,

the

stiffness

matrix

K is

tridiagonal since

Since

K is

symmetric

and

tridiagonal, this completes

the

computation

ofK.

Next,

we

have

We

compute

as

follows

(as

suggested

above,

the

computations involving

<^o

and

(f)

n

must

be

handled separately from those involving

</»i,

^2,

• •

•,

(f>n-i)-'

272

Chapter

6.

Heat flow

and

diffusion

is a solution for any constant C, and that

x

3

x

2

1

u(x)

=

--

+ -

--

6 4 12

is the solution satisfying

u(l)

= 0.

We will use a regular grid with the finite element method. We define

Xi

=

ih,

i =

0,1,

...

,

n,

h =

lin.

With piecewise linear finite elements,

as

we

have seen

before, the stiffness matrix K is tridiagonal since

Ii -

il

> 1

:::}

ixi

(x)

a:;

(x) = ° on (0,

f).

We compute

as

follows (as suggested above, the computations involving

CPo

and

CPn

must

be

handled separately from those involving

CPl,

CP2,

...

,

CPn-l):

-

..

_l(Hl)h

(dCPi

) 2

_l(Hl)h

~

_

~

K .. - d (x)

dx-

h

2dx

-

h'

i=1,2,

...

,n-1,

(i-l)h x (i-l)h

- r

h

(dCPO

) 2

tIl

Koo

=

io

dx (x) dx =

io

h2

dx =

h'

_

/1

(dCPn

) 2

/1

1 1

Knn

=

I-h

dx (x)

dx

=

I-h

h2

dx

=

h'

-

l(i+1)h

dCPi

dCPHI

l(i+1)h

(

1)

K

i

,i+l =

-(x)--(x)dx

=

-2"

dx

ih

dx

ih

h

1 .

= -

h'

Z = 0, 1,

...

, n -

l.

Since K is symmetric and tridiagonal, this completes the computation

of

K.

Next,

we

have

h =

l(HI)h

(x

-

~)

CPi(X)

dx

(i-I)h 2

=

lih

(x

_

~)

(x

- (i -

l)h)

dx

(i-I)h 2 h

+

I~HI)h

(x

_

~)

(1

_ x

~

ih)

dx

= ih2 -

~

4'

io

=

Io

h

(x

-

~)

(1

-

~)

dx

h

2

h

6-4'

in=

!~h(x-~)X-(~-h)dX

h h

2

---

4 6

6.5.

Finite

elements

and

Neumann

conditions

273

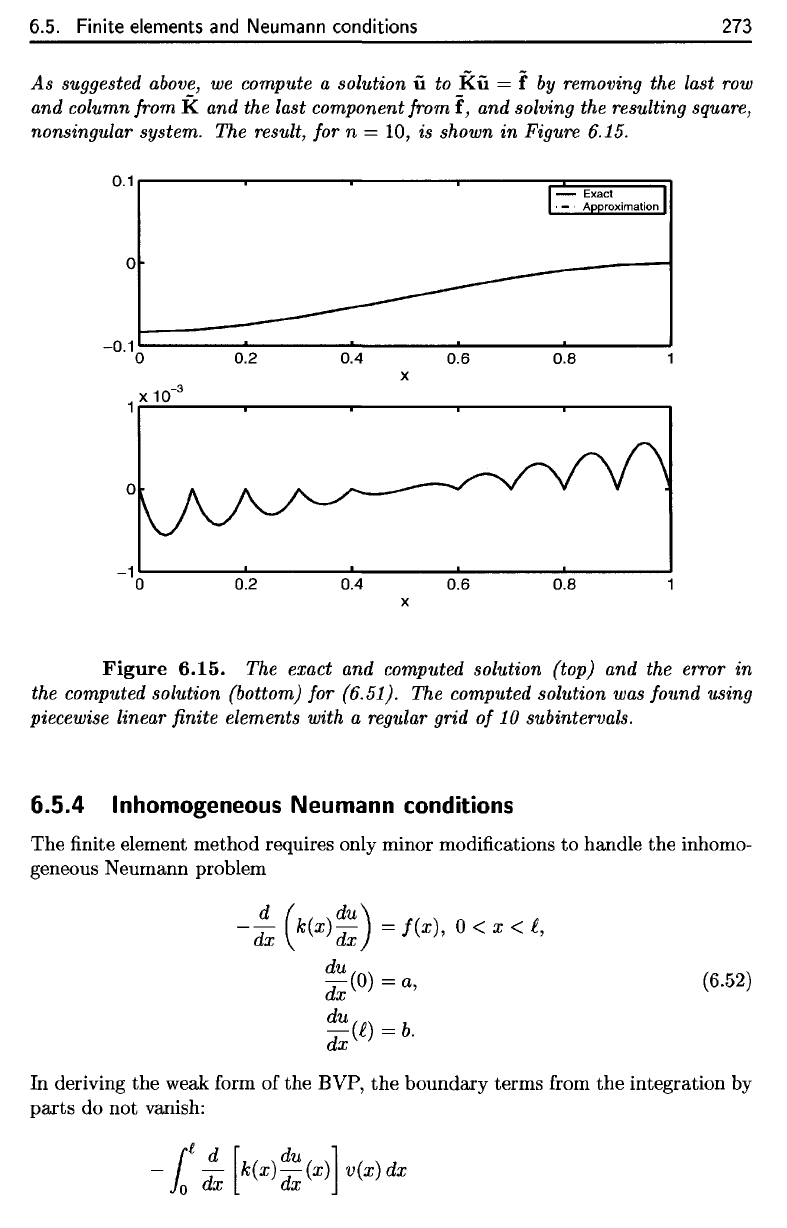
As

suggested

above,

we

compute

a

solution

u

to

Ku

= f by

removing

the

last

row

and

column from

K

and the

last component from

f,

and

solving

the

resulting square,

nonsingular system.

The

result,

for n = 10, is

shown

in

Figure 6.15.

Figure

6.15.

The

exact

and

computed solution (top)

and the

error

in

the

computed solution (bottom)

for

(6.51).

The

computed solution

was

found using

piecewise

linear

finite

elements with

a

regular

grid

of 10

subintervals.

6.5.4

Inhomogeneous

Neumann conditions

The

finite

element method requires only minor modifications

to

handle

the

inhomo-

geneous

Neumann problem

In

deriving

the

weak

form

of the

BVP,

the

boundary

terms

from

the

integration

by

parts

do not

vanish:

6.5. Finite elements

and

Neumann conditions

273

As

suggested

above,

we

compute a solution

ii

to

Kii

= f

by

removing the last row

and column from

K and the last component from

f,

and solving the resulting square,

nonsingular system. The result, for n = 10, is shown in Figure 6.15.

0.1

r----r-----"T"""""---....---,=:::;;::;;:::=:::;,

o

-0.1~------~--------~------~--------~------~

o

-3

1 x

10

0.2 0.4 0.6 0.8

x

-1~---~---~---~----~--~

o

0.2 0.4 0.6 0.8

x

Figure

6.15.

The exact and computed solution (top) and the error in

the computed solution (bottom) for

(6.

51}.

The computed solution was found using

piecewise linear finite elements with a regular grid

of

10 subintervals.

6.5.4 Inhomogeneous Neumann conditions

The

finite element method requires only minor modifications

to

handle

the

inhomo-

geneous Neumann problem

d (

dU)

- dx

k(x)dx

=f(x),o<x<i!,

du

dx

(0)

=

a,

(6.52)

~~

(f) =

b.

In deriving

the

weak form of

the

BVP,

the

boundary terms from

the

integration by

parts

do

not

vanish:

r£

d [ du ]

-

io

dx k(x) dx (x) v(x) dx

274

Chapter

6.

Heat flow

and

diffusion

The

weak form becomes

When

we

apply

the

Galerkin

method,

we end up

with

a

slightly

different

right-

hand-side

vector

f.

We

have

Example 6.11.

We now

apply

the finite

element method

to the

inhomogeneous

Neumann

problem

The

exact solution

is

(again

choosing

the

solution with

u(l]

=

Q).

The

calculations

are

exactly

the

same

as

for

Example

6.10,

except that

the first and

last components

of f are

altered

as

given

in

(6.54)-

We

therefore

have

The

results

are

shown,

for

n

= 10, in

Figure

6.16.

6.5.5

The

finite element method

for an

IBVP

with Neumann

conditions

We

now

briefly consider

the

following

IBVP:

274

Chapter

6.

Heat flow

and

diffusion

The

weak form becomes

find u E V such

that

a(u,

v)

=

(f,

v)

+

k(R)v(R)b

-

k(O)v(O)a

for all v E

V.

(6.53)

When

we apply

the

Galerkin method, we end

up

with a slightly different right-

hand-side vector

f.

We

have

ii

=

(f,

rPi)

+

k(R)rPi(R)b

-

k(O)rPi(O)a

_ {

(f,

rP~)'

~

::

1,2,

....

, n - 1

~ince

rPi(R~

=

rPi(O)

= 0),

-

(f,

rP~)

-

k(O)a,

~

- 0 (smce

rPo(R)

- 0,

rPo(O)

- 1),

(f,

rPi)

+

k(R)b,

i = n (since

rPn(R)

=

1,

rPn(O)

= 0).

(6.54)

Example

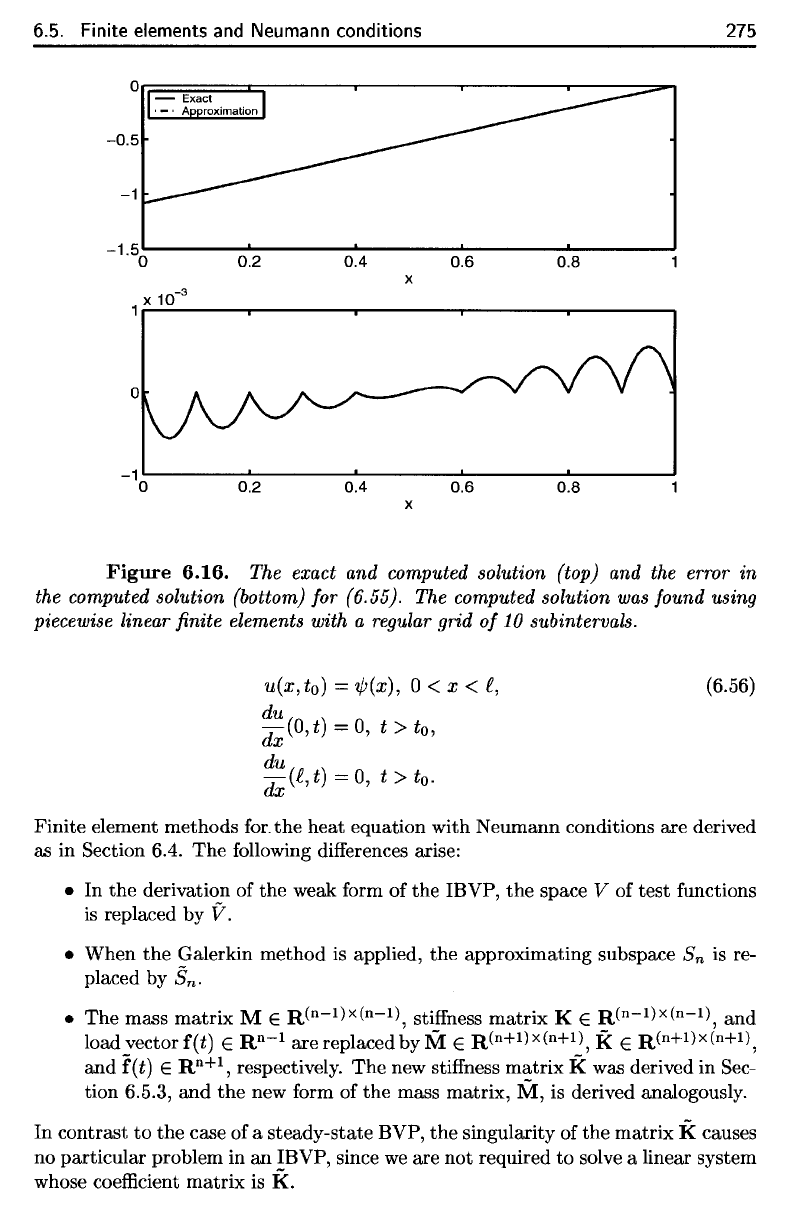
6.11.

We now apply the finite element method to the inhomogeneous

Neumann

problem

The exact solution is

d

2

u 1

-

dx

2

= X -

2'

0 < x < 1,

du

(0)

=

1,

dx

dU(l) =

1.

dx

x

3

x

2

13

u(x)

=

-6

+

'4

+x

-

12

(6.55)

(again choosing the solution with

u(l)

= 0). The calculations

are

exactly the same

as

for Example 6.10, except that the first and last components

of

f

are

altered

as

given

in

(6.54). We therefore have

- h

2

h - h h

2

fo

= 6 - 4 - 1, fn = 4 - 6 +

1.

The results

are

shown, for n = 10,

in

Figure 6.16.

6.5.5 The finite element method

for

an

IBVP with Neumann

conditions

We now briefly consider

the

following IBVP:

au

a

2

u

pc

at -

'"

ax

2

=

f(x,

t), 0 < x <

R,

t>

to,

6.5.

Finite

elements

and

Neumann

conditions

275

Figure

6.16.

The

exact

and

computed

solution

(top)

and the

error

in

the

computed

solution (bottom)

for

(6.55).

The

computed

solution

was

found

using

piecewise

linear

finite

elements with

a

regular

grid

of 10

subintervals.

Finite element methods

for.

the

heat equation with Neumann conditions

are

derived

as in

Section

6.4.

The

following

differences

arise:

• In the

derivation

of the

weak

form

of the

IBVP,

the

space

V of

test

functions

is

replaced

by

V.

•

When

the

Galerkin method

is

applied,

the

approximating subspace

S

n

is re-

placed

by

S

n

.

• The

mass matrix

M

e

R(

n

-

1

)

x

(

n

-

1

),

stiffness

matrix

K €

RC

11

-

1

)^"-

1

),

and

load

vector

f(t)

G

R

11

"

1

are

replaced

by M €

R(n+i)x(n+i)

?

£

e

R(n+i)x(n+i)

}

and

f(t)

G

R

n+1

,

respectively.

The new

stiffness

matrix

K was

derived

in

Sec-

tion 6.5.3,

and the new

form

of the

mass matrix,

M, is

derived analogously.

In

contrast

to the

case

of a

steady-state

BVP,

the

singularity

of the

matrix

K

causes

no

particular problem

in an

IBVP, since

we are not

required

to

solve

a

linear system

whose

coefficient

matrix

is K.

6.5. Finite elements

and

Neumann conditions 275

_1.51-

___

-'-

___

---'

.......

___

-'-

___

--L

___

--J

o

0.2

0.4

0.6 0.8

x

_1~------~---------L--

______

~

________

~

______

~

o

0.2

0.4 0.6

0.8

x

Figure

6.16.

The exact and computed solution {top} and the error in

the computed solution {bottom} for

{6.55}.

The computed solution

was

found using

piecewise linear finite elements with a regular grid

of

10 subintervals.

u(x, to) =

'l/J(x),

0<

x <

e,

du

dx

(0, t) = 0, t > to,

du

dx

(e,

t) = 0, t > to·

(6.56)

Finite element methods

for.

the

heat equation with Neumann conditions are derived

as in Section 6.4.

The

following differences arise:

• In

the

derivation of the weak form of the IBVP,

the

space V of test functions

is

replaced by if.

• When

the

Galerkin method is applied,

the

approximating subspace Sn is re-

placed by

Sn.

•

The

mass matrix M E

R(n-l)x(n-l),

stiffness

matrix

K E

R(n-l)x(n-l),

and

load vector f(t) E

Rn-l

are replaced by

ME

R(n+l)

x

(n+l)

,K

E

R(n+1)x

(n+1)

,

and f(t) E

Rn+l,

respectively.

The

new stiffness matrix K was derived in Sec-

tion 6.5.3,

and

the

new form of

the

mass matrix,

M,

is derived analogously.

In

contrast

to

the

case of a steady-state BVP,

the

singularity of

the

matrix

K causes

no particular problem in

an

IBVP, since

we

are not required

to

solve a linear system

whose coefficient matrix is

K.

276

Chapter

6.

Heat

flow

and

diffusion

Moreover,

the

source

function

f(x,t)

is not

required

to

satisfy

a

compatibility

condition

in

order

for

(6.56)

to

have

a

solution. Physically, this makes sense. Think-

ing

of

heat

flow, for

example,

the

temperature distribution

is in

general changing,

so

there

is no

inconsistency

in

having

a net

gain

or

loss

of

total

heat

energy

in the

bar.

On the

other hand,

for the

steady-state

case,

the

temperature could

not be

independent

of

time

if the

total

amount

of

heat

energy

in the bar

were

changing

with

time.

This

can

also

be

seen directly.

If u is the

solution

of

(6.56),

then

This

last

expression

is

(proportional

to) the

time

rate

of

change

of the

total

heal

energy contained

in the bar

(see (2.2)

in

Section 2.1).

We

leave

the

detailed formulation

of a

piecewise linear

finite

element

method

for

(6.56)

to the

exercises (see Exercise

6).

Exercises

1.

Consider

an

aluminum

bar of

length

1 m and

radius

1 cm.

Suppose

that

the

sides

and

ends

of the bar are

perfectly

insulated,

and

heat energy

is

added

to

the

interior

of the bar at a

rate

of

(x

is

given

in

centimeters,

and the

usual coordinate system

is

used).

The

thermal conductivity

of the

aluminum alloy

is

1.5W/(cmK).

Find

and

graph

the

steady-state

temperature

of the

bar.

Use the finite

element method.

2.

Repeat

the

previous exercise, except

now

assume

that

the bar is

heteroge-

neous,

with thermal conductivity

3.

Consider

a

copper

bar

(thermal conductivity 4.04

W/(cm

K)) of

length

100 cm.

Suppose

that

heat

energy

is

added

to the

interior

of the bar at the

constant

276

Chapter

6.

Heat flow

and

diffusion

Moreover, the source function

I(x,

t) is not required

to

satisfy a compatibility

condition in order for (6.56) to have a solution. Physically, this makes sense. Think-

ing of

heat

flow,

for example, the temperature distribution

is

in general changing,

so there

is

no inconsistency in having a

net

gain or loss of

total

heat energy in

the

bar. On

the

other hand, for the steady-state case, the temperature could not be

independent of time

if

the

total

amount of heat energy in the bar were changing

with time.

This can also

be

seen directly.

If

u is

the

solution of (6.56),

then

fof

I(x,

t) dx = fof

pc

~~

(x,

t)

dx

_fof

~

~:~

(x, t) dx

I

f

au

[au]e

=

pC-

a

(x, t) dx -

~-a

(x, t)

o t x

x=o

= fof

pc

~~

(x, t) dx -

~

(~~

(C,

t)

-

~~

(0,

t))

=

foe

pc

~~

(x, t) dx (by

the

Neumann conditions)

=

%t

[fof pcu(x, t)

dx].

This last expression

is

(proportional to) the time

rate

of change of the

total

heat

energy contained in the

bar

(see (2.2) in Section 2.1).

We

leave the detailed formulation of a piecewise linear finite element method

for (6.56)

to

the exercises (see Exercise 6).

Exercises

1.

Consider

an

aluminum

bar

of length 1 m

and

radius 1 cm. Suppose

that

the

sides

and

ends of the

bar

are perfectly insulated, and heat energy

is

added

to

the interior of the

bar

at

a

rate

of

1

I(x)

=

10-

7

x(25 - x) (100 - x) +

240

W

/cm

3

(x

is

given in centimeters,

and

the usual coordinate system

is

used).

The

thermal conductivity

ofthe

aluminum alloy

is

1.5 W / (cm K). Find and graph

the

steady-state temperature of the bar. Use the finite element method.

2.

Repeat the previous exercise, except now assume

that

the

bar

is

heteroge-

neous, with thermal conductivity

~(x)

= 1.0 +

(1~0)

2

3. Consider a copper

bar

(thermal conductivity 4.04 W / (cm K)) oflength 100 cm.

Suppose

that

heat energy

is

added to the interior of the

bar

at

the

constant

6.5.

Finite

elements

and

Neumann

conditions

277

rate

of

f(x)

=

0.005

W/cm

3

,

and

that

heat energy

is

added

to the

left

end

(x

= 0) of the bar at the

rate

of

0.01

W/cm

2

.

(a)

At

what

rate

must

heat

energy

be

removed

from

the

right

end (x =

100)

in

order

that

a

steady-state

solution exist? (See Exercise

6.2.5a,

or

just

use

common

sense.)

(b)

Formulate

the BVP

leading

to a

steady-state solution,

and

approximate

the

solution using

the

finite

element method.

4.

Suppose

that,

in the

Neumann problem

(6.44),

/

does

not

satisfy

the

com-

patibility condition

Suppose

we

just ignore this fact

and try to

apply

the

finite

element method

anyway. Where does

the

method break down? Illustrate with

the

Neumann

problem

5.

The

purpose

of

this exercise

is to

provide

a

sketch

of the

proof

that

the

null

space

of K is

spanned

by

u

c

,

where

K is the

stiffness

matrix arising

in a

Neumann problem

and

u

c

is the

vector with each component equal

to

one.

(a)

Suppose

Ku = 0,

where

the

components

of u are

UQ,

ui,...,

u

n

.

Show

that

this implies

that

a(v,v)

=0,

where

(Hint:

Compute

u •

Ku.)

(b)

Explain

why

a(v,

v) = 0

implies

that

v is a

constant function.

(c)

Now

explain

why Ku = 0

implies

that

u is a

multiple

of

u

c

.

6. (a)

Formulate

the

weak

form

of

(6.56).

(b)

Show

how to use

piecewise linear

finite

elements

and the

method

of

lines

to

reduce

the

weak

form

to a

system

of

ODEs.

(c)

Using

the

backward

Euler

method

for the

time integration, estimate

the

solution

of the

IBVP

6.5. Finite elements

and

Neumann conditions

277

rate

of

f(x)

=

0.005W/cm

3

,

and

that

heat energy is added

to

the

left end

(x =

0)

of

the

bar

at

the

rate

of 0.01

W/cm

2

.

(a) At what

rate

must heat energy be removed from

the

right end

(x

= 100)

in order

that

a steady-state solution exist? (See Exercise 6.2.5a, or

just

use common sense.)

(b) Formulate

the

BVP

leading

to

a steady-state solution,

and

approximate

the

solution using

the

finite element method.

4.

Suppose

that,

in

the

Neumann problem (6.44), f does

not

satisfy

the

com-

patibility condition

f-

lo

f(x)dx

=

o.

Suppose

we

just

ignore this fact

and

try

to

apply

the

finite element method

anyway. Where does

the

method break down? illustrate with

the

Neumann

problem

d

2

u

- dx

2

= x,

~~(O)

=

0,

~~(1)

=0.

O<x<l

5.

The

purpose of this exercise

is

to

provide a sketch of

the

proof

that

the

null

space of

K is spanned by U

c

,

where K

is

the

stiffness

matrix

arising in a

Neumann problem

and

U

c

is

the

vector with each component equal

to

one.

(a) Suppose

Ku

=

0,

where

the

components of u are

UO,Ul,

..•

,Un.

Show

that

this implies

that

a(

v,

v)

=

0,

where

(Hint: Compute

U·

Ku.)

n

V = L

Ui¢>i·

i=O

(b) Explain why a( v, v) = 0 implies

that

v

is

a constant function.

(c) Now explain why

Ku

= 0 implies

that

u is a multiple of U

c

•

6.

(a) Formulate

the

weak form of (6.56).

(b) Show how

to

use piecewise linear finite elements

and

the

method of lines

to

reduce

the

weak form

to

a system of ODEs.

(

c)

Using

the

backward Euler method for

the

time integration, estimate

the

solution of

the

IBVP

au

_ a

2

u = 0

at

ax2 ' 0

<.x

<

1,

t >

0,

Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

Подождите немного. Документ загружается.