Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

54

The

material

on the

delta

function

found

in

Section

4.6 or

Section

5.7 is

needed

for

this

exercise.

358

Chapter

8.

Problems

in

multiple

spatial

dimensions

11.

Consider

a

square drumhead occupying

the

unit square,

when

at

rest,

and

suppose

the

drum

is

"plucked"

so

that

its

initial (vertical)

displacement

is the

(piecewise linear)

function

Here

0

=

1(T

4

and

(see

Figure 8.9). Find

the

resulting vibrations

of the

drumhead

by

solving

12. Let ft be the

rectangle

(8.10).

Define

Let LN '•

Cpf(ft)

—>

C(ft)

be

defined

by

L^u

=

—Aw.

Use

separation

of

variables

to find the

eigenpairs

of LN

with

separated

eigenfunctions.

13.

54

Suppose

an

elastic membrane occupies

the

unit square,

and

something pushes

up at the

center

of the

membrane

(a pin or the tip

of

a

pencil,

for

example).

The

purpose

of

this question

is to

determine

the

resulting shape

of the

membrane.

This

can be

done

by

solving

the BVP

Graph

the

solution. Note:

The

Fourier

coefficients

of the

point source

can be

found

using

the

sifting

property

of the

Dirac delta

function.

358

Chapter

8.

Problems

in

multiple spatial dimensions

11. Consider a square drumhead occupying

the

unit square,

o =

{(Xl,

X2)

E

R2

: 0 <

Xl

<

1,

0 <

X2

< I} ,

when

at

rest, and suppose

the

drum

is "plucked" so

that

its initial (vertical)

displacement is

the

(piecewise linear) function

Here

f3

=

10-

4

and

(X1,X2)

E 0

1

,

(Xl,

X2)

E O

2

,

(Xl,

X2)

E 0

3

,

(X1,X2)

E 0

4

.

01

= {(X1,X2) E

R2

02 = {(X1,X2) E R2

0

3

= {(X1,X2) E

R2

04

= {(X1,X2) E R2

o <

X2

<

!,

X2

<

Xl

< 1 -

X2}

,

! <

Xl

<

1,

1 -

Xl

<

X2

<

xI},

! <

X2

<

1,

1 -

X2

<

Xl

<

X2}

,

o <

Xl

<

!,

Xl

<

X2

< 1 -

Xl

}

(see Figure 8.9). Find

the

resulting vibrations of

the

drumhead by solving

(Pu

8t

2

-

c

2

~u

= 0, x E

0,

t > 0,

u(x,O) =

¢(x),

x E

0,

8u

8t

(x, 0) = 0, x E

0,

u(x, t) = 0, x E

80,

t >

o.

12. Let fl

be

the

rectangle (8.10). Define

civ(n) =

{u

E C

2

(n) :

~~(x)

= 0, x E aO}.

Let

LN

:

Civen)

-+

C(O) be defined by

LNu

=

-~u.

Use separation of

variables

to

find

the

eigenpairs of

LN

with separated eigenfunctions.

13.

54 Suppose

an

elastic membrane occupies

the

unit square,

0=

{(XI,X2) ER2 :

O<xI<I,

0<x2<1},

and

something pushes up

at

the

center of

the

membrane (a pin or

the

tip

of a pencil, for example).

The

purpose of this question is

to

determine

the

resulting shape of

the

membrane. This can be done

by

solving

the

BVP

-~u

=

8(XI

- 1/2)8(x2 -

1/2)

in fl,

u = 0 on

00.

Graph

the

solution. Note:

The

Fourier coefficients of

the

point source can be

found using

the

sifting

property

of

the

Dirac delta function.

5

4

The

material

on

the

delta

function found in Section 4.6

or

Section 5.7 is needed for this

exercise.

8.3. Fourier

series

on a

disk

359

Figure

8.9.

The

partition

of

the

unit

square

used

in

Exercise

11.

14. Let

(7

be the

rectangle (8.10),

and

suppose

d£l

is

partitioned

as in

(8.13).

Define

Let

L

m

:

C^(Q)

—>•

C(fi)

be

defined

by

L

m

u

=

—Aw.

Use

separation

of

variables

to find the

eigenpairs

of

L

m

with

separated

eigenfunctions.

15.

Repeat Exercise

5, but

assuming

now

that

the

edges

F2

and

Fa

are

insulated,

while

edges

FI

and

F4

are

placed

in an ice

bath

(dft

is

partitioned

as in

(8.13)).

(You

will

need

the

eigenpairs determined

in

Exercise 14.)

8.3

Fourier

series

on a

disk

We

now

discuss another simple two-dimensional domain

for

which

we can

derive

Fourier series methods, namely,

the

case

of a

circular disk.

We

define

where

A > 0 is a

constant.

We

wish

to

develop Fourier series methods

for the

following

Dirichlet problem:

8.3. Fourier

series

on

a disk

359

Figure

8.9.

The partition

of

the unit square used

in

Exercise

11.

14. Let n be the rectangle (8.10), and suppose

an

is

partitioned as in (8.13).

Define

Let

Lm :

C!(O)

-+

C(O) be defined by

Lmu

=

-~u.

Use separation of

variables

to

find the eigenpairs of Lm with separated eigenfunctions.

15. Repeat Exercise

5,

but

assuming now

that

the

edges r

2

and

r3

are insulated,

while edges

r

1

and

r

4

are placed in

an

ice

bath

(an

is

partitioned as in (8.13)).

(You will need

the

eigenpairs determined in Exercise 14.)

8.3 Fourier

series

on

a

disk

We

now discuss another simple two-dimensional domain for which

we

can derive

Fourier series methods, namely, the case of a circular disk.

We

define

where

A > 0

is

a constant.

We

wish

to

develop Fourier series methods for the

following Dirichlet problem:

-~U

=

f(x),

x E

n,

u(x)

= 0, x E

an.

(8.29)

360

Chapter

8.

Problems

in

multiple spatial dimensions

The first

step

is to find the

eigenvalues

and

eigenfunctions

of the

Laplacian, subject

to the

Dirichlet

conditions

on the

circle.

We

have only

one

technique

for finding

eigenfunctions

of a

differential

operator

in

two

variables, namely separation

of

variables. However, this technique

is not

very

promising

in

rectangular coordinates, since

the

boundary condition does

not

separate.

For

this reason,

we first

change

to

polar coordinates.

If we

define

where

(r, 9) are the

polar coordinates corresponding

to the

rectangular coordinates

(#1,0:2),

then

the

Dirichlet condition becomes simply

If

we

apply

separation

of

variables

and

write

v(r,0)

=

R(r)T(0),

then

the

Dirichlet

condition

is

R(A}T(9]

= 0 for all 0,

which implies

(if v is

nontrivial)

that

R(A]

= 0.

The use of

polar coordinates introduces periodic boundary conditions

for

T:

There

is

also

a

boundary condition

for R at r = 0,

although

it is not one we

have

seen

before.

We

simply need

that

R(Q)

be a finite

number.

8.3.1

The

Laplacian

in

polar coordinates

Before

we can

apply separation

of

variables

to the

PDE,

we

must change variables

to

determine

the

form

of the

(negative) Laplacian

in

polar coordinates. This

is an

exercise

in the

chain rule,

as we now

explain.

The

chain rule implies,

for

example,

that

This

allows

us to

replace

the

partial derivative with respect

to

x\

by

partial

deriva-

tives

with respect

to the new

variables

r and

0,

provided

we can

compute

To

deal with derivatives with respect

to

#2,

we

will

also need

It is

straightforward

to

compute

the

needed derivatives

from

the

relationship

between

rectangular

and

polar coordinates:

360

Chapter

8.

Problems

in

multiple spatial dimensions

The first step is

to

find the eigenvalues

and

eigenfunctions of the Laplacian, subject

to

the

Dirichlet conditions on the circle.

We

have only one technique for finding eigenfunctions of a differential operator

in two variables, namely separation of variables. However, this technique

is

not

very promising in rectangular coordinates, since

the

boundary condition does not

separate. For this reason,

we

first change

to

polar coordinates.

If

we

define

v(r,O) =

U(Xl,X2),

where

(r,O)

are

the

polar coordinates corresponding to the rectangular coordinates

(Xl,X2),

then the Dirichlet condition becomes simply

v(A,O) = 0, -7r::; 0 <

7r.

If

we

apply separation of variables and write v(r,

0)

= R(r)T(O),

then

the Dirichlet

condition

is

R(A)T(O) = 0 for all

0,

which implies

(if

v

is

nontrivial)

that

R(A) =

O.

The

use of polar coordinates introduces periodic boundary conditions for T:

T(-7r) =

T(7r),

dT dT

dO

(-7r) =

dO

(7r).

There is also a boundary condition for R

at

r = 0, although

it

is

not

one

we

have

seen before.

We

simply need

that

R(O)

be a finite number.

B.3.1 The

Laplacian

in

polar

coordinates

Before

we

can apply separation

of

variables

to

the

PDE,

we

must change variables

to

determine the form of

the

(negative) Laplacian in polar coordinates. This

is

an

exercise in

the

chain rule, as

we

now explain.

The

chain rule implies, for example,

that

OU

OV

or

OV

00

-=--+--.

OXl

or

OXl

00

OXl

This allows us to replace the partial derivative with respect to

Xl

by partial deriva-

tives with respect

to

the new variables r and

0,

provided

we

can compute

or

00

OX1'

OX1·

To deal with derivatives with respect

to

X2,

we

will also need

ar

ao

OX2'

aX2·

It

is straightforward to compute the needed derivatives from

the

relationship

between rectangular and polar coordinates:

Xl

= r cos

(0),

r =

VXi

+

x~,

X2 = r sin

(0),

X2

tan

(0)

=

-.

Xl

8.3. Fourier

series

on a

disk

361

We

have

and, similarly,

Also,

and, similarly,

We

collect these formulas

for

future

reference:

We

can now

compute

the

Laplacian

in

polar coordinates.

We

have

and so

8.3.

Fourier

series

on

a

disk

We

have

Xl

= r

cos

(61)

=

cos

(61)

y'xi +

x~

r '

and, similarly,

Also,

:r

= sin

(61).

UX2

X2

tan(61)=-

Xl

::::}

sec

2

(61)

861

= _

X2

= _ r sin

(61)

8XI

xi

r2

cos

2

(61)

861

sin

(61)

::::}-----

8XI

-

r'

and, similarly,

861

cos

(61)

8X2

r

We

collect these formulas

for

future reference:

:r

=cos(61),

:r

= sin

(61),

UXI

UX2

861

sin

(61)

861

cos

(61)

r

We

can

now

compute the Laplacian in polar coordinates.

We

have

and

so

8u 8v

8r

8v

861

-=--+--

8XI

8r

8XI

861

8XI

=

cos

(61)

8v _ sin

(61)

8v

8r

r

80'

8

2

u

(8

2

v

8r

8

2

v 861) .

861

8v

8xI

=

cos

(61)

8r2

8XI

+

8618r

8XI

- sm

(61)

8XI

8r

_ sin

(61)

(8

2

v

8r

+ 8

2

v

861

) _ r

cos

(B)

It

-sin

(B)

'*

8v

r

8r861

8XI

861

2

8XI

r2

8B

=

(l1)

(

(l1)

8

2

v _ sin

(61)

8

2

v)

sin

2

(61)

8v

cos

Q

cos

Q

8r2

r

8618r

+ r

8r

_ sin

(61)

(

(l1)

8

2

v _ sin

(61)

8

2

v)

2 sin

(61)

cos

(61)

8v

r

cos

Q 8r8B r

861

2

+

r2

80

=

cos

2

(61)

8

2

v _ 2 sin

(61)

cos

(B)

8

2

v + sin

2

(61)

8

2

v + sin

2

(B)

8v

8r2

r 808r

r2

861

2

r

8r

2 sin

(B)

cos

(61)

8v

+

r2

861·

361

362

Chapter

8.

Problems

in

multiple spatial dimensions

A

similar calculation shows

that

Adding

these

two

results

and

using

the

identity

cos

2

(0) +

sin

2

(9) = 1, we

obtain

where

we

write

—

A

p

for the

Laplacian

in

polar coordinates.

8.3.2 Separation

of

variables

in

polar

coordinates

We

now

apply

separation

of

variables,

and

look

for

eigenfunctions

of

—A

p

(under

Dirichlet

conditions)

of the

form

That

is, we

wish

to find all

solutions

of

that

have

the

form

v(r,9)

=

R(r}T(0).

Substituting

the

separated

function

v = RT

into

the PDE

yields

the

following:

Since

the

left

side

of

this equation

is a

function

of 0

alone,

while

the

right side

is a

function

of r

alone, both sides must

be

constant.

We

will

write

or

362

Chapter

8.

Problems

in

multiple spatial dimensions

A similar calculation shows

that

(Pu

. 2

(0)

8

2

v 2 sin

(0)

cos

(0)

8

2

v cos

2

(0)

8

2

v cos

2

(0)

8v

- =

SIn

- +

--

+ +

-----'--'-

8x~

8r2

r a08r

r2

80

2

r

8r

2 sin

(0)

cos

(0)

8v

r2

80'

Adding these two results

and

using

the

identity

cos

2

(0)

+ sin

2

(0)

= 1,

we

obtain

8

2

v 1 8

2

v

18v

-Apv

= -

8r2

- r

2

80

2

-

-:;.

8r'

where

we

write

-Ap

for the Laplacian in polar coordinates.

8.3.2 Separation of variables

in

polar coordinates

We

now apply separation of variables,

and

look for eigenfunctions of

-Ap

(under

Dirichlet conditions) of

the

form

v(r,

0)

= R(r)T(O).

That

is,

we

wish

to

find all solutions of

-Apv

=

Av

in

n,

v = 0 on

an

(8.30)

that

have

the

form v(r,O) = R(r)T(O). Substituting the separated function v =

RT

into the

PDE

yields the following:

-Apv

=

Av

8

2

v 1 8

2

v

18v

::::}--------=Av

8r2

r2

80

2

r 8r

d2R

1 d

2

T 1 dR

::::}

--T-

-R-

-

--T=

ART

dr

2

r2

d0

2

r

dr

::::}

_R-1

d

2

R _

~T-I

d2T _

~R-I

dR = A

dr2

r2

d0

2

r

dr

-1 d2T 2

-1

2 d

2

R

-1

dR

::::}

- T

d0

2

=

Ar

+ R r

dr

2

+ R r

dr'

Since the left side of this equation is a function of 0 alone, while

the

right side

is

a

function of

r alone,

both

sides must be constant.

We

will write

or

8.3. Fourier

series

on a

disk

363

We

then

have

or

This

last

equation

can be

written

as an

eigenvalue problem

for

R,

but it is not one

we

have studied before.

We

will

study

it in

detail below,

but first we

deal with

the

easier eigenvalue problem

for T.

As

we

mentioned above,

the

angular variable

0

introduces periodic boundary

conditions

for T, so we

must solve

the

eigenvalue problem

As

we saw in

Section 6.3,

the

eigenvalues

are 0 and

n

2

,

n =

1,2,3,

— The

constant

function

1 is an

eigenfunction

corresponding

to 7 = 0, and

each positive eigenvalue

7 =

n

2

has two

independent eigenfunctions,

cos

(nO)

and sin

(nO).

8.3.3

Bessel's

equation

We

now

consider

the

problem

We

know

that

A

must

be

positive, since

the

Laplacian

has

only positive eigenvalues

under Dirichlet conditions (see Section

8.2.1).

We can

considerably

simplify

the

analysis

by the

change

of

variables

We

define

so

tnat

and

8.3. Fourier

series

on

a disk 363

We

then

have

or

eF

R +

~

dR

+

(A

_ 2) R =

o.

dr

2

r

dr

r2

This last equation can be written as

an

eigenvalue problem for

R,

but

it

is

not one

we

have studied before.

We

will study

it

in detail below,

but

first

we

deal with the

easier eigenvalue problem for

T.

As

we

mentioned above,

the

angular variable 0 introduces periodic boundary

conditions for

T,

so

we

must solve

the

eigenvalue problem

eFT

- d(}2 ='YT,

-1f<O<1f,

T(

-1f) = T(1f), (8.31)

dT dT

dO

(-1f) = d(}

(1f).

As

we

saw in Section 6.3, the eigenvalues are 0

and

n

2

,

n =

1,2,3,

....

The

constant

function 1 is

an

eigenfunction corresponding

to

'Y

=

0,

and each positive eigenvalue

'Y

= n

2

has two independent eigenfunctions, cos

(nO)

and

sin

(nO).

8.3.3

Bessel's

equation

We

now consider the problem

eFR

+

~

dR +

(A

_ 2) R =

0,

dr

2

r

dr

r2

R(O)

E

R,

(8.32)

R(A) =

o.

We

know

that

A must be positive, since the Laplacian has only positive eigenvalues

under Dirichlet conditions (see Section 8.2.1).

We

can considerably simplify

the

analysis by

the

change of variables

s =

v>"r.

We

define

S(s) = R

(Jx)

¢}

R(r) = S

(VXr)

,

so

that

dR(r) =

V>..dS

(V>..r)

=

V>..dS

(s)

dr

ds

and

364

Chapter

8.

Problems

in

multiple

spatial

dimensions

We

then

have

The ODE

is

called Bessel's

equation

of

order

n.

In the new

variables,

the BVP

(8.32) becomes

Bessel's

equation does

not

have solutions

that

can be

expressed

in

terms

of

elementary

functions.

To find a

solution

of

Bessel's equation,

we can use a

power

series

expansion

of the

solution.

We

suppose

55

that

(8.33)

has a

solution

of the

form

The

value

of

a,

as

well

as the

coefficients

005^15^2,

• •

•,

must

be

determined

from

the

differential

equation

and

boundary conditions.

We

have

and so

55

This

is yet

another example

of an

inspired guess

at the

form

of a

solution.

It is

based

on the

fact

that

Euler's equation,

Also,

has

solutions

of the

form

R(r)

=

r

a

.

364

Chapter

8.

Problems

in

multiple spatial dimensions

We

then have

The ODE

dl S +

~

dS +

(1

_

n2)

S = 0

ds

2

S

ds

S2

is

called Bessel's equation

of

order n. In the new variables, the BVP (8.32) becomes

dl8

1 d8 (

n2)

- + - - + 1 - - 8 =

0,

ds

2

S

ds

s2

8(0) E R,

(8.33)

S

(v'XA)

=

O.

Bessel's equation does not have solutions

that

can be expressed in terms of

elementary functions.

To

find a solution of Bessel's equation,

we

can use a power

series expansion of

the

solution.

We

suppose

55

that

(8.33) has a solution of the

form

00 00

8(s) = r

a

Laksk

=

LakSk+a,

ao

f:.

O.

k=O k=O

The value of a, as

well

as the coefficients aO,al,a2,

...

, must be determined from

the differential equation and boundary conditions.

We

have

and so

(8.34)

Also,

dlS

00

ds

2

(s)

=

L(k

+

a)(k

+ a -

1)

ak

s

k+

a

-2.

k=O

(8.35)

55This is yet

another

example

of

an

inspired guess

at

the

form

of

a solution.

It

is based on

the

fact

that

Euler's equation,

2d

2

R

dR

r - + r - -

>'R

= 0,

dr

2

dr

has solutions

of

the

form R(

r)

=

rO;

.

8.3. Fourier

series

on a

disk

365

It is

helpful

to

write

Substituting (8.36), (8.34),

and

(8.35)

into

Bessel's equation yields

or

This

equation implies

that

the

coefficient

of

each power

of s

must vanish,

and so we

obtain

the

equations

which

simplify

to

We

have assumed

that

ao

/

0, so the first

equation

in

(8.37) implies

that

Moreover,

the

condition

that

5(0)

be finite

rules

out the

possibility

that

a =

—n,

so

we

conclude

that

must hold. This, together with

the

second equation

in

(8.37), immediately implies

that

The

third

equation

in

(8.37)

can be

written

as the

recursion relation

8.3. Fourier

series

on

a disk

365

It

is

helpful to write

00

S(s)

=

Laksk+a

=

Lak_2Sk+a-2.

(8.36)

k=O

k=2

Substituting (8.36), (8.34), and (8.35) into Bessel's equation yields

00

L(k

+ o:)(k +

0:

-

1)

ak

s

k+

a

-2

+

L(k

+ 0:)akSk+a-2

k=O k=O

00 00

+ L ak_2

Sk

+

a

-

2

- n

2

L ak

sk

+

a

-

2

= 0,

k=2

k=O

or

00

+ L

{((k

+ o:)(k +

0:

-

1)

- n

2

)ak +

ak-d

Sk+

a

-

2

= 0.

k=2

This equation implies

that

the coefficient of each power of s must vanish, and so

we

obtain the equations

(0:(0:

-

1)

+

0:

- n

2

)ao

=

0,

((0:

+

1)0:

+

(0:

+

1)

- n

2

)al

= 0,

((k

+ o:)(k +

0:

-

1)

+

(k

+

0:)

- n

2

)ak +

ak-2

= 0, k =

2,3,4,

...

,

which simplify

to

(0:

2

-

n

2

)

ao

= 0,

((0:+1)2-n2)al=0,

((k

+

0:)2

- n

2

)

ak +

ak-2

=

0,

k =

2,3,4,

....

(8.37)

We

have assumed

that

ao

::j:.

0,

so

the

first equation in (8.37) implies

that

0:=

±n.

Moreover,

the

condition

that

S(O)

be finite rules out the possibility

that

0: =

-n,

so

we

conclude

that

o:=n

must hold. This, together with the second equation in (8.37), immediately implies

that

al

= 0.

The

third

equation in (8.37) can be written as the recursion relation

ak-2 ak-2

ak = - (k + n)2 _ n2 = -

k(k

+

2n)'

k =

2,3,4,....

(8.38)

56

Standard

software

packages,

including

MATLAB,

Mathematica,

and

Maple,

implement Bessel

functions

just

as

they

do

elementary

functions

such

as the

natural logarithm

or

sine.

366

Chapter

8.

Problems

in

multiple

spatial dimensions

Since

a\

= 0,

(8.38)

implies

that

all of the odd

coefficients

are

zero:

On

the

other hand,

we

have

and,

in

general,

Since

any

multiple

of a

solution

of

(8.33)

is

again

a

solution,

we may as

well choose

the

value

of

ao

to

give

as

simple

a

formula

as

possible

for

a

2

j

• For

this reason,

we

choose

and

obtain

We

then obtain

the

solution

This function

is a

solution

of

Bessel's equation

of

order

n.

It is

usually written

and

called

the

Bessel function

of

order

n. The

reader should note

that

the

above

calculations

are

valid

for n = 0 as

well

asn

=

l,2,3,

—

8.3.4 Properties

of the

Bessel

functions

The

Bessel functions have been extensively studied because

of

their

utility

in

applied

mathematics,

and

their properties

are

well

known.

56

We

will

need

the

following

properties

of the

Bessel functions:

1. If n > 0,

then

J

n

(0)

= 0.

This

follows

directly

from

(8.40).

366

Chapter

8. Problems

in

multiple spatial dimensions

Since

al

= 0, (8.38) implies

that

all of

the

odd

coefficients are zero:

a2i+1

= 0, j = 0, 1,

2,

....

On

the

other

hand,

we

have

ao

a - -

2 - - 2(2 + 2n) - - 22(n +

1)'

a2

ao

a4

= - 4(4 + 2n) =

2!2

4

(n

+ 1)(n +

2)'

a4

ao

a6

= - 6(6 + 2n) = -

3!2

6

(n +

l)(n

+ 2)(n +

3)'

and, in general,

(-I)

ia

o .

a2i

= j!2

2i

(n + 1)(n +

2)

...

(n +

j)'

J =

0,1,2,

....

(8.39)

Since any multiple of a solution of (8.33) is again a solution,

we

may as well choose

the

value of

ao

to

give as simple a formula as possible for a2i' For this reason,

we

choose

and

obtain

1

ao

= 2nn!

(-I)i

.

a2i

= 22i+nj!(n +

j)!'

J =

0,1,2,

....

We

then

obtain

the

solution

00

(

-1)i

(S

)

2i+n

S(s) =

~

j!(n

+ j)! 2 .

This function is a solution of Bessel's equation of order n.

It

is usually written

00

(-I)i

(S)2i+n

In(s) =

~

j!(n

+ j)! 2

(8.40)

and

called

the

Bessel function

of

order

n.

The

reader should note

that

the

above

calculations are valid for

n = ° as well as n =

1,2,3,

....

8.3.4 Properties of the

Bessel

functions

The

Bessel functions have been extensively studied because of their utility in applied

mathematics,

and

their properties are well known.

56

We

will need

the

following

properties of

the

Bessel functions:

1.

If

n > 0,

then

In(O) =

0.

This follows directly from (8.40).

56

Standard

software packages, including MATLAB, Mathematica,

and

Maple,

implement

Bessel

functions

just

as

they

do elementary functions such as

the

natural

logarithm

or

sine.

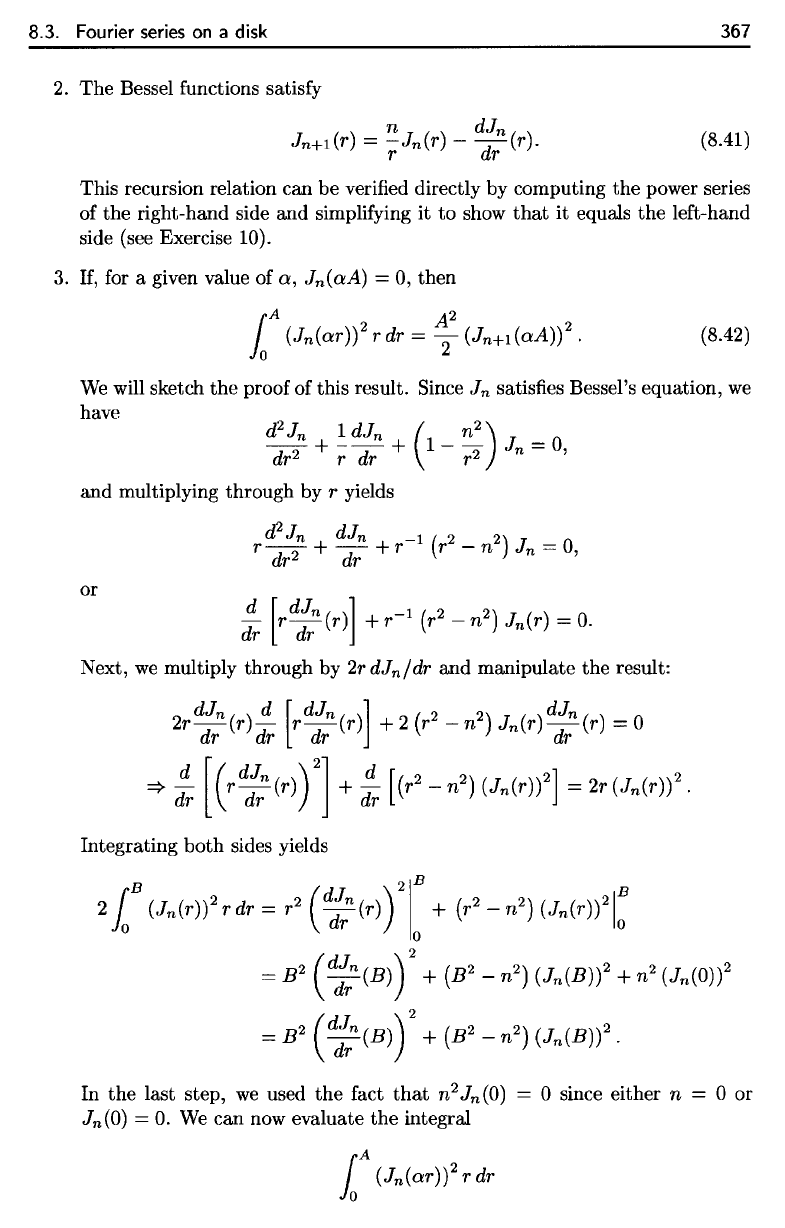
8.3. Fourier

series

on a

disk

367

2.

The

Bessel functions satisfy

This recursion relation

can be

verified

directly

by

computing

the

power series

of

the

right-hand side

and

simplifying

it to

show

that

it

equals

the

left-hand

side

(see Exercise 10).

3. If, for a

given value

of a,

J

n

(aA)

— 0,

then

In

the

last

step,

we

used

the

fact

that

n

2

J

n

(0)

=

0

since either

n = 0 or

J

n

(0)

= 0. We can now

evaluate

the

integral

We

will

sketch

the

proof

of

this result. Since

J

n

satisfies Bessel's equation,

we

have

and

multiplying through

by r

yields

or

Next,

we

multiply through

by

2rdJ

n

/dr

and

manipulate

the

result:

Integrating both sides yields

8.3. Fourier

series

on

a disk

367

2.

The

Bessel functions satisfy

(8.41)

This recursion relation can

be

verified directly by computing

the

power series

of the right-hand side and simplifying

it

to

show

that

it

equals

the

left-hand

side (see Exercise 10).

3.

If, for a given value of

a,

In(aA) = 0, then

(8.42)

We

will sketch

the

proof of this result. Since I

n

satisfies Bessel's equation,

we

have

d

2

J

n

1dJ

n

(

n2)

dr2

+ r

dr

+

1-

r2

I

n

=

0,

and multiplying through by r yields

d

2

J

n

dJ

n

-1

( 2

2)

r

dr

2

+

dr

+ r r - n I

n

= 0,

or

!

[r

d~n

(r)]

+

r-

1

(r2

- n

2

) In(r) =

O.

Next,

we

multiply through by

2rdJ

n

/dr

and manipulate the result:

2r

d~n

(r)!

[r

d~n

(r)]

+ 2

(r2

- n

2

) In(r)

d~n

(r)

= 0

~

! [

(r

d~n

(r))

2]

+ !

[(r2

_ n

2

) (In(r))2] =

2r

(I

n

(r))2 .

Integrating

both

sides yields

In

the

last step,

we

used the fact

that

n

2

J

n

(0)

= 0 since either n = 0 or

In(O)

=

O.

We

can now evaluate

the

integral

Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods

Подождите немного. Документ загружается.