Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


418
Chapter
9.
More about Fourier
series
The
Fourier series
of
f
even
is the
cosine series
of /, so,
again,
the
convergence
of
the
cosine series
can be
examined
in
terms
of the
convergence
of a
related Fourier
series.
Figure
9.6
shows
the odd and
even extensions
of / :
[-1,1]
->•
R
defined
by
f(x)
= 1 + x.
Figure
9.6.
The
function
f(x}
=
l
+ x and its odd
(left)
and
even
(right)
extensions.
Exercises
1.
Compute
the
Fourier sine series
of
f(x)
= x on the
interval
[—1,1]
and
graph
the sum of the first 50
terms
on the
interval
[—3,3].
To
what
function
does
the
series appear
to
converge?
What
is the
period
of
this
function?
2.
Compute
the
Fourier cosine series
of
f(x)
= x on the
interval
[—1,1]
and
graph
it on the
interval
[—3,3].
To
what
function
does
the
series
appear
to
converge?
What
is the
period
of
this
function?
Then,
by the
previous theorem,
the
(full)
Fourier series
of
f
0
dd
is the
sine series
of /,
so the
convergence
of the
sine series
can be
understood
in
terms
of the
convergence
of
a
related
(full)
Fourier series.
Similarly,
given
/ :
(0,^)
->
R, we
define
f
even
:
(—£,£)
->
R, the
even
extension
of /, by
418
Chapter 9. More about Fourier
series
Then, by the previous theorem,
the
(full) Fourier series of
fodd
is
the sine series of
f,
so
the
convergence of the sine series can be understood in terms of
the
convergence
of a related (full) Fourier series.
Similarly, given
f : (0,
f)
--t
R,
we
define
feven
:
(-f,
f) --t
R,
the even
extension
of
f,
by
{
f(x),
0 < x <
f,
feven(x) =
f(
-x),
-f
< x <
O.
The Fourier series of
feven
is
the cosine series of
f,
so, again, the convergence of
the
cosine series can be examined in terms of
the
convergence of a related Fourier
series.
Figure 9.6 shows the odd and even extensions of f :
[-1,1]
--t R defined by
f(x)
= 1 + x.
2
1
>-
0
-1
-2
~.
-2
-1
~
~
~
v
~'
o
X
1
2
,
,
1
>-
0
-1
-2
2
-2
-1
,
,
,
V
o
x
1 2
Figure
9.6.
The function
f(x)
= 1 + x and its
odd
(left) and even (right)
extensions.
Exercises
1. Compute the Fourier sine series of
f(x)
= x on the interval
[-1,1]
and graph
the sum of the first
50
terms on the interval
[-3,3].
To
what function does
the series appear
to
converge?
What
is
the period of this function?
2.
Compute the Fourier cosine series of
f(x)
= x on the interval
[-1,1]
and
graph it on the interval
[-3,3].
To what function does
the
series appear
to
converge?
What
is
the
period of this function?

9.4.
Pointwise
convergence
of
Fourier series
419
3.
Suppose
/ :
[0,^]
—>•
R is
continuous.
(a)
Under what conditions
is
f
0
dd
continuous?
(b)
Under what conditions
is
f
even
continuous?
4.
Consider
a
function
/ :
[—•£,•£]
—>•
R, and let
c
n
,
n = 0,
±1,±2,...
be its
complex
Fourier
coefficients.
(a)
Suppose
/ is
odd.
What
special property
do the
coefficients
c
n
,
n
=
0,
±1,
±2,...
have?
(b)
Suppose
/ is
even.
What
special property
do the
coefficients
c
n
,
n =
0,
±1,
±2,...
have?
5.
Show
how to
relate
the
quarter-wave
sine series
of / :
[0,£|
->
R to the
full
Fourier series
of a
related
function.
(Hint: This other function
will
be
denned
on
the
interval
[-2^,2^].)
6.
Show
how to
relate
the
quarter-wave
cosine series
of / : [0,
t]
—>•
R to the
full
Fourier series
of a
related function. (Hint: This other function
will
be
defined
on
the
interval
[-2^,2^].)
9.4
Pointwise convergence
of
Fourier
series
Given
the
relationships
that
exist among
the
various Fourier series,
it
suffices
to
discuss
the
convergence
of
complex Fourier series.
The
convergence
of
other series,
such
as the
Fourier sine series,
will
then
follow
directly.
If
/ is a
real-
or
complex-valued
function
defined
on
[—.£,
£],
then
the
partial
sums
w
form
a
sequence
of
functions.
Before
discussing
the
convergence
of
these
partial
sums specifically,
we
describe
different
ways
in
which
a
sequence
of
functions
can
converge.
9.4.1 Modes
of
convergence
for
sequences
of
functions
Given
any
sequence
{/AT}^
=I
of
functions
defined
on [a, 6] and any
(target) function
/,
also
defined
on [a,
6],
we
define
three types
of
convergence
of the
sequence
to /.
That
is, we
assign three
different
meanings
to
"/AT
->•
/ as N
—>•
oo."
1. We say
that
{/AT}
converges
pointwise
to / on [a,
b]
if, for
each
x £ [a, 6], we
have
/jv(ar)
->•
f(x)
as N
->•
oo
(i.e.
|/(ar)
-
/AT(X)|
-)•
0 as N
->
oo).
2.
We say
that
{/AT}
converges
to / in
L
2
(or in the
mean-square sense)
if
ll/
~
/wll
—>•
0 as
./V
—>•
oo. The
reader
will
recall
that
the
(L
2
)
norm
of a
real-
9.4. Pointwise convergence
of
Fourier
series
419
3. Suppose I :
[0,
f] -+ R is continuous.
(a) Under
what
conditions
is
lodd
continuous?
(b) Under
what
conditions
is
leven
continuous?
4.
Consider a function I :
[-f,
f]
-+
R,
and let
Cn,
n = 0,
±1,
±2,
...
be its
complex Fourier coefficients.
(a) Suppose
I is odd.
What
special property do
the
coefficients
Cn,
n =
0,
±1,
±2,
...
have?
(b) Suppose
I is even.
What
special property do
the
coefficients
Cn,
n =
0,
±1,
±2,
...
have?
5. Show how
to
relate
the
quarter-wave sine series of I :
[0,
f]
-+ R
to
the
full
Fourier series of a related function. (Hint: This
other
function will
be
defined
on
the
interval
[-
2£,
2£].)
6.
Show how
to
relate
the
quarter-wave cosine series of I :
[0,
f]
-+ R
to
the
full
Fourier series of a related function. (Hint: This
other
function will be defined
on
the
interval
[-
2f,
2£].)
9.4 Pointwise convergence of Fourier
series
Given
the
relationships
that
exist among the various Fourier series,
it
suffices
to
discuss
the
convergence of complex Fourier series.
The
convergence of other series,
such as
the
Fourier sine series, will
then
follow directly.
If
I is a real- or complex-valued function defined on
[-f,
f],
then
the
partial
sums
N
IN(X) = L
cnei1fnx/l
n=-N
form a sequence of functions. Before discussing
the
convergence of these
partial
sums specifically,
we
describe different ways in which a sequence of functions can
converge.
9.4.1 Modes of convergence for
sequences
of functions
Given any sequence {IN
}]V'=1
offunctions defined on
[a,
b]
and any (target) function
I,
also defined on
[a,
b],
we
define three types of convergence of
the
sequence
to
I.
That
is,
we
assign three different meanings
to
"IN
-+
I as N
-+
00."
1.
We
say
that
{IN}
converges pointwise
to
I on
[a,
b]
if, for each x E
[a,
b],
we
have IN(X)
-+
I(x)
as N
-+
00
(Le.
If(x) - fN(X) I
-+
° as N
-+
(0).
2.
We
say
that
{IN} converges
to
I in
L2
(or in the mean-square sense) if
111-
INII
-+
° as N
-+
00.
The
reader will recall
that
the
(L2)
norm of a real-

Therefore,
/TV
—>
f in the
mean-square sense means
that
420
Chapter
9.
More
about Fourier
series
or
complex-valued
function
g on [a,
b]
is
3. We say
that
{/AT}
converges
to /
uniformly
on [a,
b]
if
Actually, this definition
is
stated
correctly only
if all of the
functions involved
are
continuous,
so
that
the
maximum
is
guaranteed
to
exist.
The
general
definition
is:
{/AT}
converges
to /
uniformly
on [a,
b]
if,
given
any e > 0,
there exists
a
positive integer
N
e
such
that,
if N
>
N
e
and x e [a,
6],
then
\f(x)
—
/TV(X)|
< e. The
intuitive meaning
of
this
definition
is
that,
given
any
small tolerance
e, by
going
far
enough
out in the
sequence,
/N
will
approximate
/ to
within this tolerance
uniformly,
that
is, on the
entire interval.
The
following
theorem shows
that
the
uniform
convergence
of a
sequence
im-
plies
its
convergence
in the
other
two
senses. This theorem
is
followed
by
examples
that
show
that
no
other conclusions
can be
drawn
in
general.
Theorem
9.8.
Let
{/AT}
be a
sequence
of
complex-valued
functions
defined
on
[a,6].
//
this
sequence
converges
uniformly
on
[a,b]
to f
:
[a,b]
-»
C,
then
it
also
converges
to f
pointwise
and in the
mean-square sense.
Proof.
See
Exercise
5.
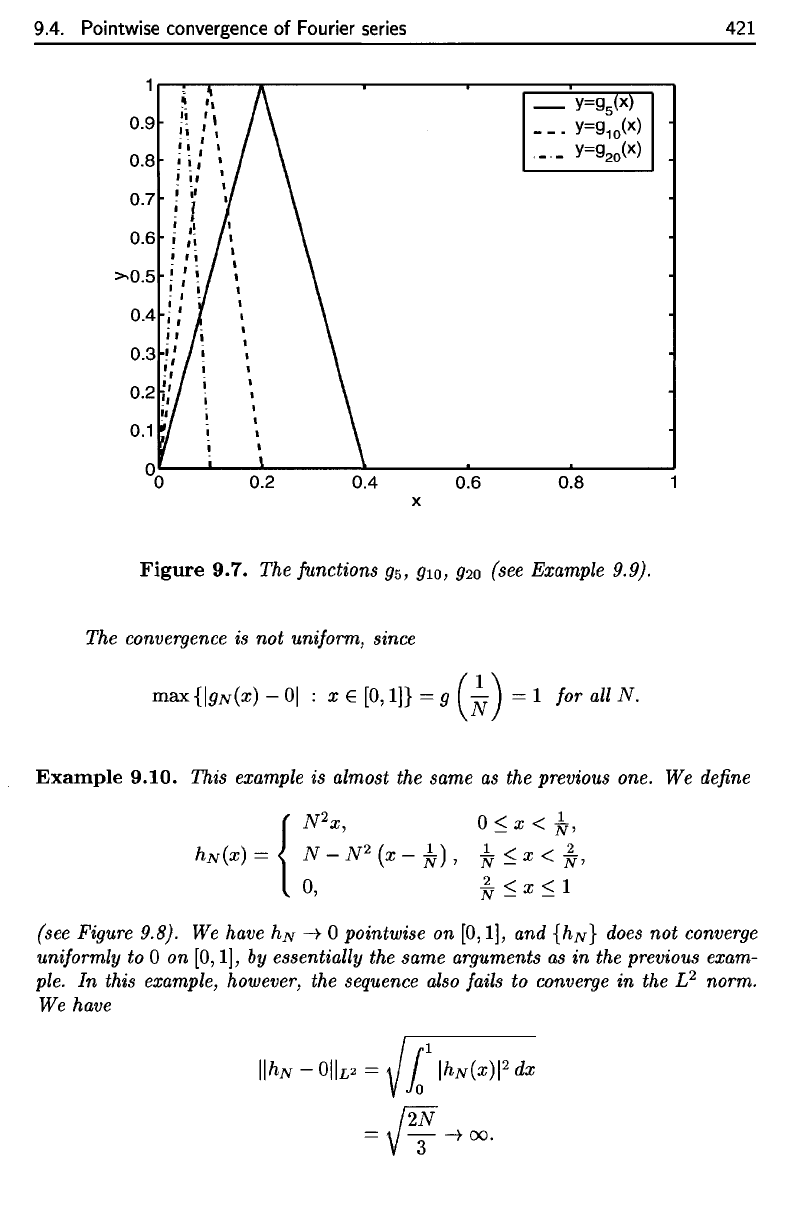
Example
9.9.
We
define
Figure
9.7
shows
the
graphs
of
g§,
giQ,
and
#20
•
Then {gN}
converges
pointwise
to the
zero function.
Indeed,
pAr(O)
= 0 for all
N,
so
clearly
pAr(O)
-»
0, and if
0
< x
<
1,
then
for N
sufficiently
large,
2/N
< x.
Therefore
gN(x)
= 0 for all N
sufficiently
large,
and so
gN(x)
—>
0.
A
direct
calculation shows that
gN
—>•
0 in
L
2
:
420
Chapter 9. More about Fourier
series
or
complex-valued function 9 on
[a,
b]
is
Therefore, fN
-+
f in
the
mean-square sense means
that
lb
If(x) -
fN(X)12
dx
-+
0 as n
-+
00.
3.
We
say
that
UN}
converges to f uniformly on
[a,
b]
if
max
{If(x)
-
fN(X)1
: x E
[a,
b]}
-+
0 as N
-+
00.
Actually, this definition
is
stated
correctly only if all of the functions involved
are continuous, so
that
the maximum
is
guaranteed to exist.
The
general
definition
is:
UN}
converges
to
f uniformly on
[a,
b]
if, given any t > 0,
there exists a positive integer
N,
such
that,
if N
~
N,
and x E
[a,
b],
then
If(x) -
fN(X)1
<
t.
The
intuitive meaning of this definition
is
that,
given any
small tolerance
t,
by going far enough
out
in
the
sequence, fN will approximate
f
to
within this tolerance uniformly,
that
is, on the entire interval.
The
following theorem shows
that
the
uniform convergence of a sequence im-
plies its convergence in
the
other two senses. This theorem
is
followed by examples
that
show
that
no other conclusions can be drawn in general.
Theorem
9.S.
Let
{fN}
be
a sequence
of
complex-valued functions defined on
[a,b].
If
this sequence converges uniformly on
[a,b]
to
f : [a,b]-+
C,
then
it
also
converges to f pointwise and in the mean-square sense.
Proof.
See Exercise
5.
0
Example
9.9.
We
define
{
Nx,
gN(X)
= 1 - N
(x
-
*')
,
0,
O::;X<*"
1 < 2
N - x <
N'
i.r::;x::;1.
Figure 9.7 shows the
graphs
of
g5,
g1O,
and
g20·
Then {gN} converges pointwise
to the
zero
function. Indeed,
gN(O)
= 0 for
all
N,
so
clearly
gN(O)
-+
0, and
if
0<
x
::;
1,
then for N sufficiently
large,
2/N
< x. Therefore gN(X) = 0 for
all
N
sufficiently
large,
and
so
gN(X)
-+
O.
A direct calculation shows that
gN
-+
0 in L2:
9.4. Pointwise convergence
of
Fourier
series
421
Figure
9.7.
The
functions
g$,
gw,
#20
(see Example
9.9).
The
convergence
is not
uniform, since
(see
Figure
9.8).
We
have
HN
->
0
pointwise
on
[0,1],
and
{h^}
does
not
converge
uniformly
to 0 on
[0,1],
by
essentially
the
same arguments
as in the
previous exam-
ple.
In
this example, however,
the
sequence
also
fails
to
converge
in the L
2
norm.
We
have
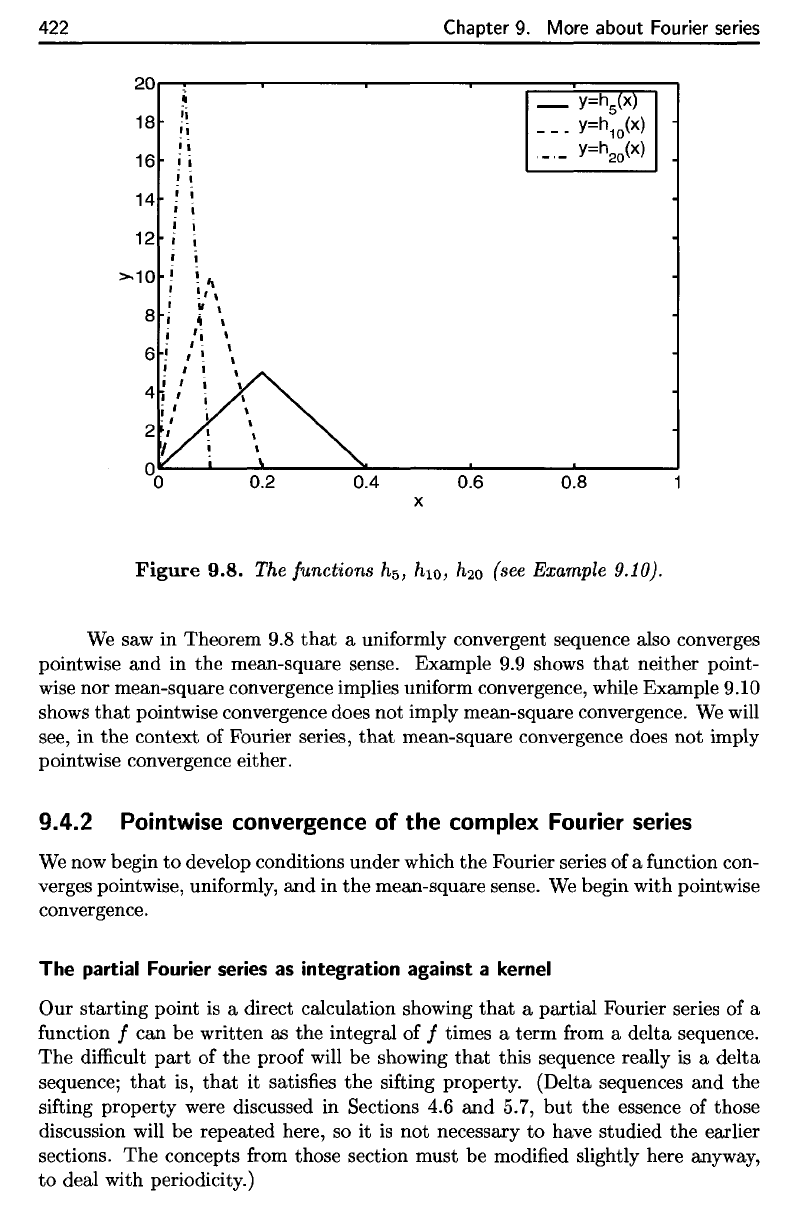
Example
9.10.
This example
is
almost
the
same
as the
previous
one.
We
define
9.4. Pointwise convergence
of
Fourier series
0.9
0.8
0.7
0.6
>-0.5
0.4
0.1
II
I
if
i I
- .
~
J~
!
,I
0.2
0.4
-
Y=9
5
X
-
_.
Y=9
10
(x)
.
_.
_
Y=9
20
(X)
0.6
0.8
x
Figure
9.7. The functions
95,910,920
(see Example 9.9).
The convergence is
not
uniform, since
max {19N(x) -
01
: x E
[0,
I)}
= g
(~)
= 1 for all N.
421
Example
9.10.
This example is almost the same as the previous one. We define
osx<:kr,
1 < 2
fij
_ X <
fij,
~
S x S 1
(see Figure 9.8). We have
hN
-+
0 pointwise on [0,1], and
{hN}
does
not
converge
uniformly to
0 on [0,1], by essentially the same arguments
as
in
the previous exam-
ple.
In
this example, however, the sequence also fails to converge
in
the
L2
norm.
We have
IlhN
-
011£2
=
11
Ih
N
(x)12
dx
= f!:
-+
00.
422
Chapter
9.
More about Fourier
series
Figure
9.8.
The
functions
h^,
HIQ,
H^Q
(see Example 9.10).
We
saw in
Theorem
9.8
that
a
uniformly
convergent sequence also converges
pointwise
and in the
mean-square sense. Example
9.9
shows
that
neither point-
wise
nor
mean-square convergence implies
uniform
convergence, while Example
9.10
shows
that
pointwise convergence does
not
imply mean-square convergence.
We
will
see,
in the
context
of
Fourier
series,
that
mean-square
convergence does
not
imply
pointwise convergence either.
9.4.2
Pointwise
convergence
of the
complex
Fourier
series
We
now
begin
to
develop conditions under which
the
Fourier series
of a
function
con-
verges pointwise,
uniformly,
and in the
mean-square sense.
We
begin with pointwise
convergence.
The
partial
Fourier series
as
integration
against
a
kernel
Our
starting point
is a
direct calculation showing
that
a
partial
Fourier series
of a
function
/ can be
written
as the
integral
of /
times
a
term
from
a
delta sequence.
The
difficult
part
of the
proof
will
be
showing
that
this sequence really
is a
delta
sequence;
that
is,
that
it
satisfies
the
sifting
property. (Delta sequences
and the
sifting
property were discussed
in
Sections
4.6 and
5.7,
but the
essence
of
those
discussion
will
be
repeated here,
so it is not
necessary
to
have studied
the
earlier
sections.
The
concepts
from
those section must
be
modified
slightly here anyway,
to
deal with periodicity.)
422
18
16
Ii
14
I I
I I
I I
12
I
I I
>-10 I
I"
~
I ,
II
\
8 I
~
\
'i
,
6!
"
~
I
Chapter 9. More about Fourier series
0.2
0.4
0.6
0.8
x
Figure
9.S.
The functions
h5;
hlOJ
h
20
(see Example 9.10).
We
saw in Theorem 9.8
that
a uniformly convergent sequence also converges
pointwise and in the mean-square sense. Example 9.9 shows
that
neither point-
wise nor mean-square convergence implies uniform convergence, while Example 9.10
shows
that
pointwise convergence does not imply mean-square convergence.
We
will
see, in
the
context of Fourier series,
that
mean-square convergence does not imply
pointwise convergence either.
9.4.2 Pointwise convergence
of
the complex Fourier
series
We
now begin
to
develop conditions under which
the
Fourier series of a function con-
verges pointwise, uniformly, and in
the
mean-square sense.
We
begin with pointwise
convergence.
The
partial Fourier
series
as
integration against a kernel
Our starting point
is
a direct calculation showing
that
a partial Fourier series of a
function
f can be written as the integral of f times a
term
from a delta sequence.
The difficult
part
of the proof will be showing
that
this sequence really
is
a delta
sequence;
that
is,
that
it satisfies
the
sifting property. (Delta sequences and
the
sifting property were discussed in Sections 4.6 and 5.7,
but
the essence of those
discussion will be repeated here,
so
it
is
not necessary
to
have studied
the
earlier
sections. The concepts from those section must be modified slightly here anyway,
to
deal with periodicity.)
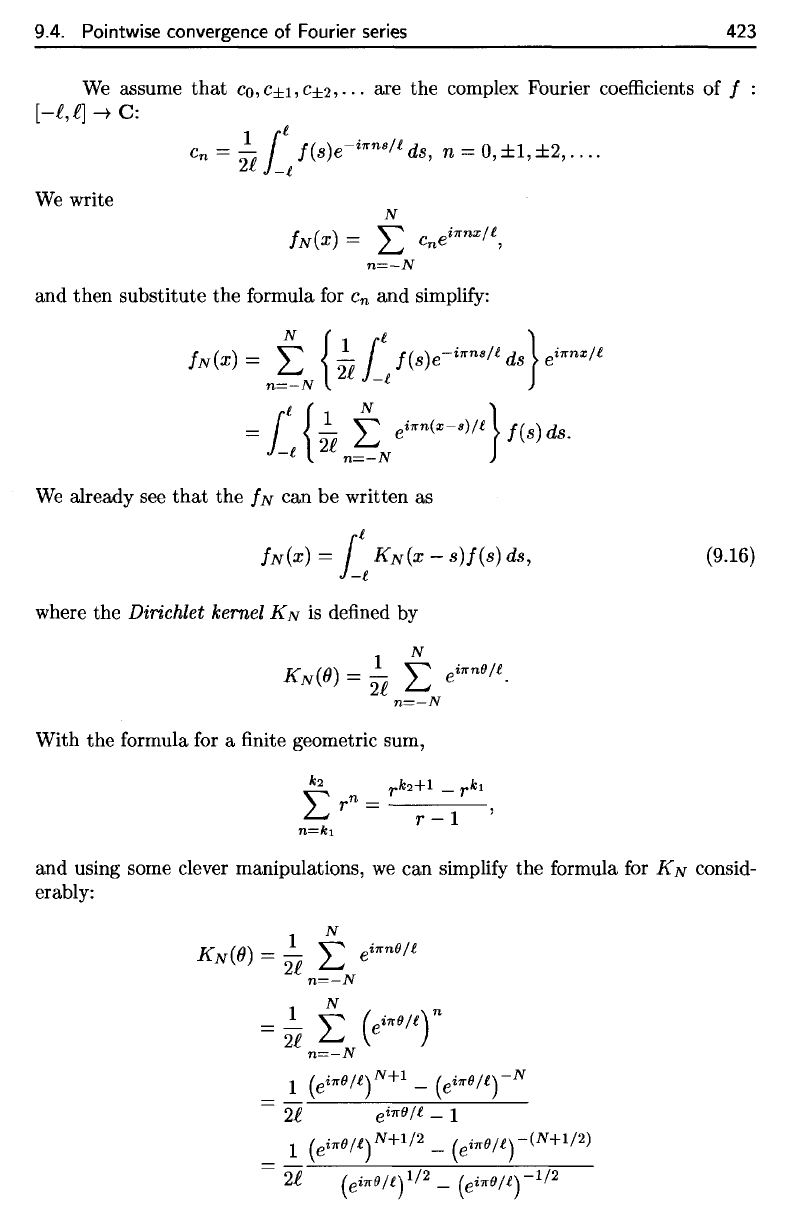
9.4.
Pointwise
convergence
of
Fourier
series
423
We
assume
that
co,c±i,c±2,...
are the
complex Fourier
coefficients
of / :
[-*,<]->C:
We
write
and
then substitute
the
formula
for
c
n
and
simplify:
We
already
see
that
the
/N
can be
written
as
where
the
Dirichlet kernel
KN
is
defined
by
With
the
formula
for a
finite
geometric
sum,
and
using some clever manipulations,
we can
simplify
the
formula
for
KN
consid-
erably:
9.4.
Pointwise
convergence
of
Fourier
series
423
We
assume
that
Co,
C±1, C±2,
.
..
are the complex Fourier coefficients of 1
[-e,e]-+
c:
C
n
=
;e
[LL
l(s)e-i7rns/L ds, n =
0,
±1, ±2,
....
We
write
n=-N
and
then
substitute the formula for C
n
and
simplify:
IN(X) =
ntN
{
;e
[LL
l(s)e-i7rns/L
dS}
ei7rnx/L
=
[LL
{
;e
ntN
e
i7rn
(x-s)/f }
I(s)
ds.
We
already see
that
the
IN
can be written as
where the
Dirichlet kernel
KN
is
defined by
With
the
formula for a finite geometric sum,
(9.16)
and using some clever manipulations,
we
can simplify the formula for
KN
consid-
erably:
1
(e
i7rli
/
i
)N+1
_
(e
i7rli
/
l
rN
U e
i7rIi
/
L
- 1
1
(e
i7rli
/
l
(+1/2
_ (ei7rIi/L) -(N+1/
2
)
U
(e
i7r
l!/f)
1/2
_
(e
i7rli
/
f
) -1/2
424
Chapter
9.
More
about Fourier series
Figure
9.9.
The
kernel
K
2
Q.
The
integral sign without limits means integration over
the
entire real line
(we do
not
discuss here conditions
on g and h
that
guarantee
that
these integrals
exists).
The
formula
for
/jv
is
similar
to a
convolution, except
that
the
integration
is
over
the finite
interval
[—1,1].
A
fundamental property
of an
ordinary convolution
is its
symmetry;
the
change
of
variables
that
replaces
x
—
s by s
yields
The
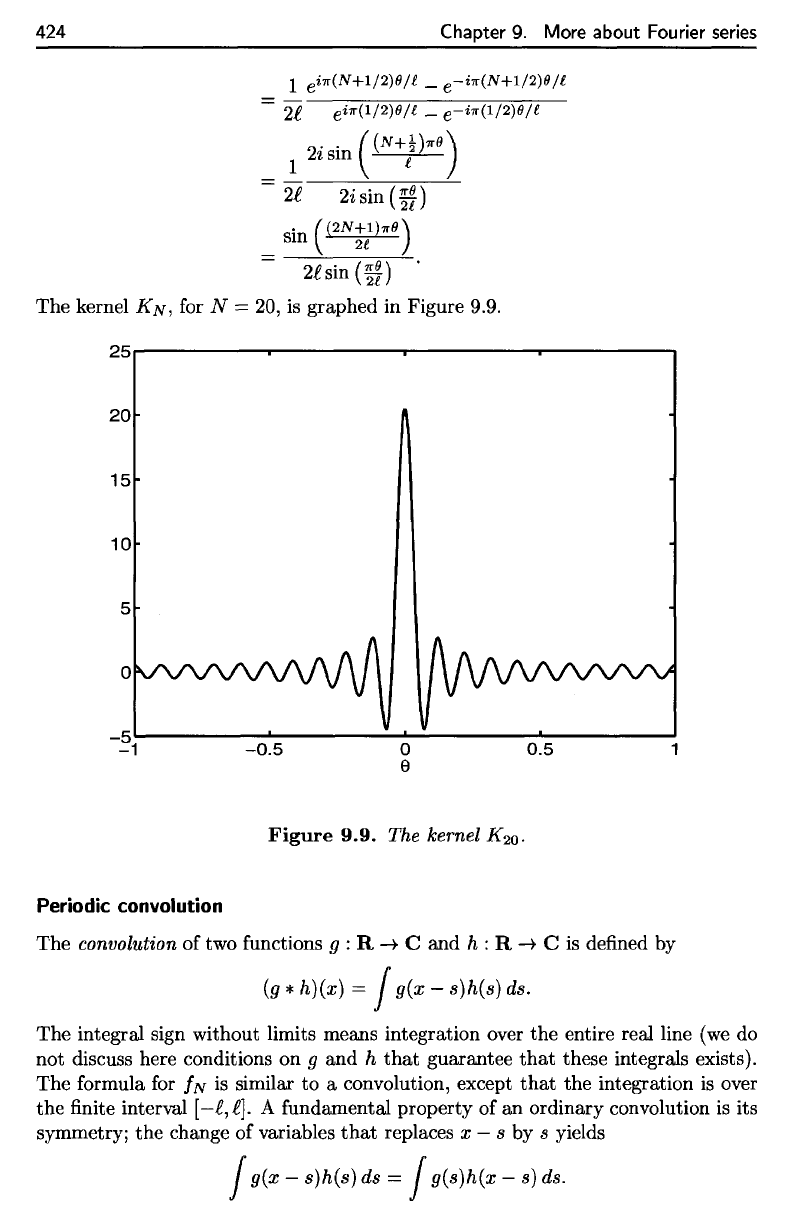
kernel
KN,
for
TV
= 20, is
graphed
in
Figure 9.9.
Periodic
convolution
The
convolution
of two
functions
g
:
R
—>
C and h
:
R
-»
C is
defined
by
424
Chapter
9.
More about Fourier
series
1 e
i
n:(N+l/2)9/l
_
e-
i
n:(N+l/2)(J/i
=
2l
e
i
n:(1/2)(J / l _
e-in:(1/2)£J
/ l
2
.,
((N+~)n:(J)
1
~sm
i
2l
2i sin (
~~
)
•
((2N+l)n:(J)
sm
2l
-
2lsin
(~n
The kernel
KN,
for N = 20,
is
graphed in Figure 9.9.
25~---------r----------~--------~----------~
20
15
10
5
Figure
9.9.
The kernel K
20
•
Periodic convolution
The convolution of two functions 9 : R
-t
C and h : R
-t
C
is
defined by
(g*h)(x)
= f
g(x-s)h(s)ds.
The integral sign without limits means integration over the entire real line
(we
do
not discuss here conditions on
9 and h
that
guarantee
that
these integrals exists).
The formula for
IN
is
similar to a convolution, except
that
the integration
is
over
the finite interval
[-f,
fl.
A fundamental property of an ordinary convolution
is
its
symmetry; the change of variables
that
replaces x - s by s yields
f g(x - s)h(s) ds = f g(s)h(x -
s)
ds.
as the
periodic convolution
of g and h.
We
can
extend
the
idea
of a
periodic convolution
to
nonperiodic functions
by
using
the
periodic extension
of a
function.
If g is
defined
on
[—£,
£],
then
its
periodic
extension
is the
function
g
per
defined
for all x G R by
For
example,
in
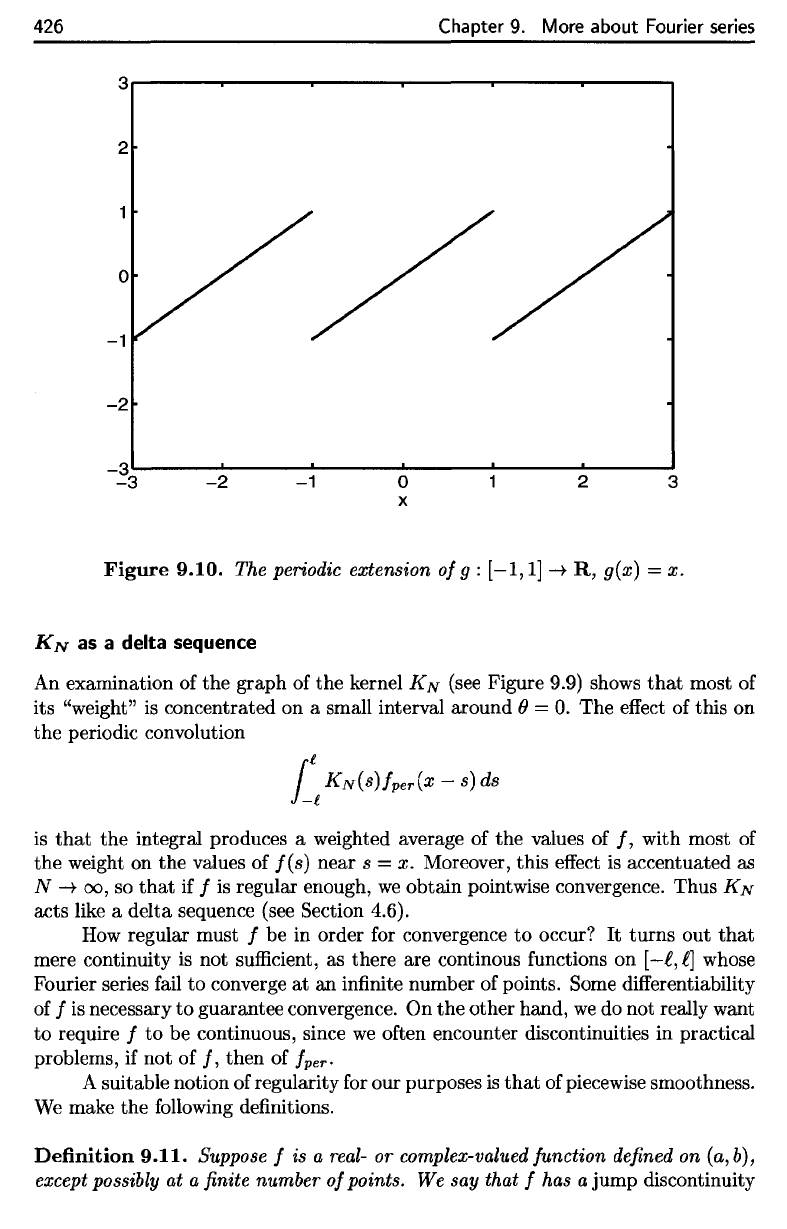
Figure 9.10
we
graph
the
function
g
per
,
where
g(x]
= x on
[—1,1].
For any g and h
defined
on
[—i,
^],
periodic
or
not,
we
interpret
the
periodic
convolution
of g and h to be
9.4.
Pointwise
convergence
of
Fourier series
425
A
similar formula holds
for
integrals such
as
that
in
(9.16), provided
the
functions
involved
are
periodic.
A
direct calculation shows
that
if
#,
h are
2^-periodic
functions defined
on R,
then
The
last
step
follows
from
the
fact
that
s
>-)•
g(s)h(x
—
s)
is
2^-periodic,
and so its
integral
over
anv
interval
of
length
21
is the
same.
We
refer
to
We
will
often
write this convolution
as
simply
but g and h are
assumed
to be
replaced
by
their periodic extensions
if
necessary
(that
is, if
they
are not
periodic).
The
kernel
KN
is
2^-periodic.
Provided
the
complex Fourier series
of /
con-
verges,
the
limit
is
obviously
a
2£-periodic
function (because each function
e
Z7rnx
^
is
2^-periodic).
Therefore,
it is
natural
to
consider
f
per
,
the
periodic extension
of
/, and to
interpret (9.16)
as a
periodic convolution.
We
then have
a
fact which
we
will
use
below.
9.4. Pointwise convergence
of
Fourier series 425
A similar formula holds for integrals such as
that
in (9.16), provided
the
functions
involved are periodic.
A direct calculation shows
that
if g,
hare
2C-periodic functions defined on
R,
then
1
£
1x+£
_/(x
- s)h(s) ds =
x-£
g(s)h(x -
s)
ds
=
1£
g(s)h(x - s) ds.
-l
The
last step follows from
the
fact
that
s
f-t
g(s)h(x -
s)
is 2C-periodic, and so its
integral over any interval of length
2C
is
the
same.
We
refer
to
as
the
periodic convolution of 9
and
h.
We
can extend
the
idea of a periodic convolution
to
nonperiodic functions by
using
the
periodic extension of a function.
If
9 is defined on
[-C,
C],
then
its periodic
extension
is
the
function
gper
defined for all x E R by
(
)
_ { g(x),
-C
< x <
C,
gper
X - g(x _
2kC),
(2k
- l)C < x <
2kC.
For example, in Figure 9.10
we
graph
the
function
gper,
where g(x) = x on
[-1,1].
For any 9
and
h defined on [-C,
C],
periodic or not,
we
interpret
the
periodic
convolution of
9
and
h
to
be
We will often write this convolution as simply
[ll
g(x - s)h(s) ds,
but
9
and
h are assumed
to
be
replaced by their periodic extensions if necessary
(that
is, if they are
not
periodic).
The
kernel
KN
is 2C-periodic. Provided
the
complex Fourier series of f con-
verges,
the
limit is obviously a 2C-periodic function (because each function e
i1fnx
/£
is 2C-periodic). Therefore,
it
is
natural
to
consider
fpen
the
periodic extension of
f,
and
to
interpret (9.16) as a periodic convolution.
We
then
have
(9.17)
a fact which
we
will use below.
426
Chapter
9.
More about
Fourier
series
Figure
9.10.
The
periodic
extension
of
g
:
[—1,1]
->
R,
g(x)
— x.
KN
as a
delta
sequence
An
examination
of the
graph
of the
kernel
K^
(see Figure 9.9) shows
that
most
of
its
"weight"
is
concentrated
on a
small interval around
0 = 0. The
effect
of
this
on
the
periodic convolution
is
that
the
integral produces
a
weighted average
of the
values
of /,
with most
of
the
weight
on the
values
of
f(s)
near
s — x.
Moreover, this
effect
is
accentuated
as
N
—>
oo,
so
that
if / is
regular enough,
we
obtain pointwise convergence. Thus
KN
acts
like
a
delta
sequence (see Section 4.6).
How
regular must
/ be in
order
for
convergence
to
occur?
It
turns
out
that
mere continuity
is not
sufficient,
as
there
are
continous
functions
on
[-€,
i]
whose
Fourier series
fail
to
converge
at an
infinite
number
of
points. Some
differentiability
of
/ is
necessary
to
guarantee convergence.
On the
other hand,
we do not
really want
to
require
/ to be
continuous, since
we
often
encounter discontinuities
in
practical
problems,
if not of /,
then
of
f
per
.
A
suitable notion
of
regularity
for our
purposes
is
that
of
piecewise smoothness.
We
make
the
following
definitions.
Definition
9.11.
Suppose
f is a
real-
or
complex-valued
function
defined
on
(a,b),
except
possibly
at a finite
number
of
points.
We say
that
f has a
jump discontinuity
426
Chapter
9.
More about Fourier
series
3r-----~------~------~------~----~------~
2
-1
-2
-3~----~----~~----~----~~----~----~
-3 -2
-1
0 2 3
x
Figure
9.10.
The periodic extension
of
9 :
[-1,1)-+
R,
g(x) =
x.
KN
as
a delta sequence
An examination of the graph of
the
kernel
KN
(see Figure 9.9) shows
that
most of
its "weight"
is
concentrated on a small interval around
()
=
O.
The effect of this on
the periodic convolution
is
that
the integral produces a weighted average of the values of
f,
with most of
the weight on
the
values of
I(s)
near s = x. Moreover, this effect
is
accentuated as
N -+
00,
so
that
if 1
is
regular enough,
we
obtain pointwise convergence. Thus
KN
acts like a delta sequence (see Section 4.6).
How regular must
1 be in order for convergence
to
occur?
It
turns out
that
mere continuity
is
not sufficient, as there are continous functions on
[-l,
l) whose
Fourier series fail to converge
at
an infinite number of points. Some differentiability
of
1
is
necessary
to
guarantee convergence. On
the
other hand,
we
do not really want
to
require f
to
be continuous, since
we
often encounter discontinuities in practical
problems, if not of
I,
then of
fper.
A suitable notion of regularity for our purposes
is
that
of piecewise smoothness.
We
make the following definitions.
Definition
9.11.
Suppose f is a real- or complex-valued function defined on (a,b),
except possibly at a finite number
of
points. We say that 1 has a jump discontinuity
9.4.
Pointwise
convergence
of
Fourier
series
427
Proof.
This
is
proved
by
direct calculation
(see
Exercise
4).
at
XQ
G
(a, b) if
both
exist
but are not
equal.
(Recall
that
if
both
one-sided limits exist
and are
equal
to
f(xo),
then
f is
continuous
at x —
XQ.)
We
say
that
f is
piecewise continuous
on (a, b) if
1. f is
continuous
at all but a finite
number
of
points
in
(a,b);
2.
every
discontinuity
of f in (a, b) is a
jump discontinuity;
3.
lim
a
._
>a
+
f(x)
and
\im.
x
_^
b
-
f(x]
exist.
Finally,
we say
that
f is
piecewise smooth
on (a, b) if
both
f and
df/dx
are
piecewise
continuous
on (a,
b).
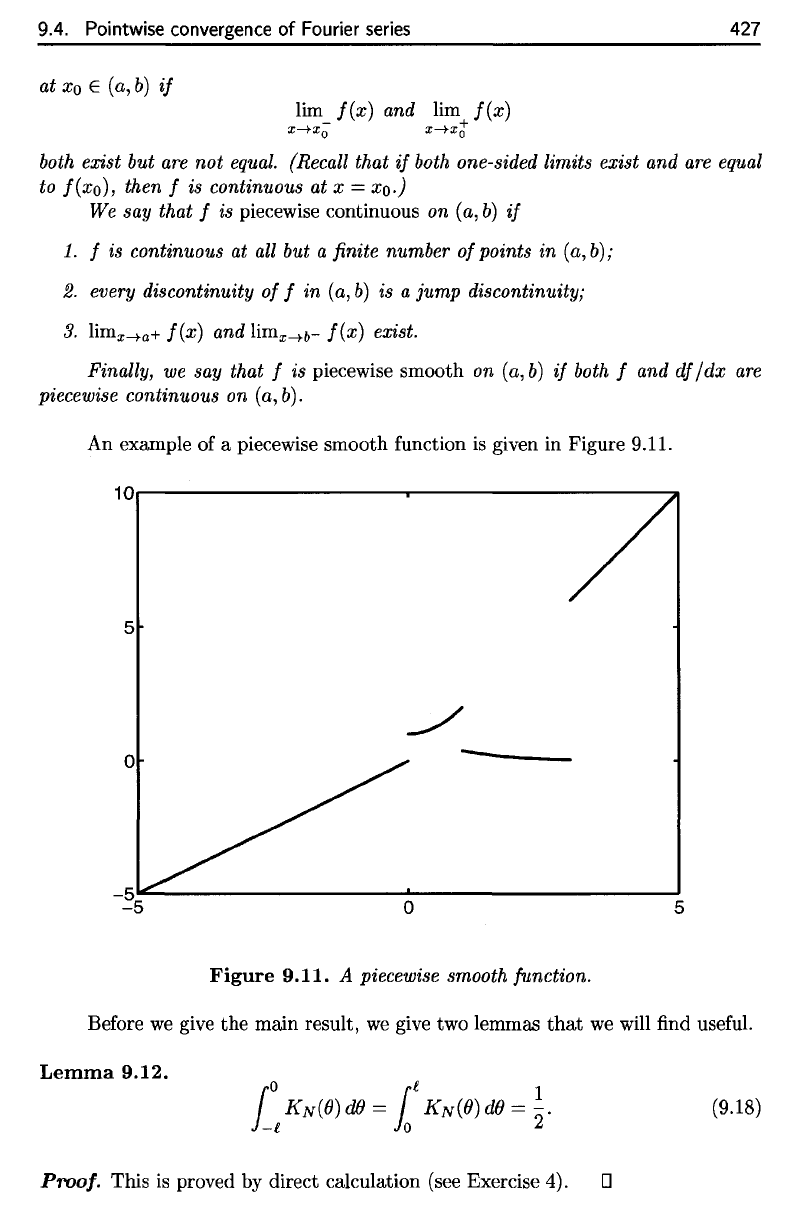
An
example
of a
piecewise smooth
function
is
given
in
Figure
9.11.
Figure 9.11.
A
piecewise smooth function.
Before
we
give
the
main result,
we
give
two
lemmas
that
we
will
find
useful.
Lemma
9.12.
9.4. Pointwise convergence
of
Fourier
series
427
at
Xo
E
(a,
b)
if
lim
f(x)
and lim
f(x)
x-tx;-
x-txci
both exist but are
not
equal. (Recall that
if
both one-sided limits exist and are equal
to
f(xo),
then f is continuous at x =
xo.)
We say that f is piecewise continuous on (a,
b)
if
1.
f is continuous at all but a finite number
of
points
in
(a, b);
2.
every discontinuity
of
f
in
(a,
b)
is a
jump
discontinuity;
3.
limx-ta+
f(x)
and limx-tb-
f(x)
exist.
Finally,
we
say that f is piecewise
smooth
on (a,
b)
if
both f and
df
Idx
are
piecewise continuous on (a, b).
An
example of a piecewise
smooth
function
is
given in Figure 9.11.
10~------------------~------------------~
5
-
5
Figure
9.11.
A piecewise smooth function.
Before
we
give
the
main
result, we give two lemmas
that
we will find useful.
Lemma
9.12.
(9.18)
Proof.
This
is
proved by direct calculation (see Exercise 4).
o
