Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


428
Chapter
9.
More about Fourier
series
The
next lemma
is
called Bessel's inequality
and
follows
directly
from
the
projection
theorem.
Lemma
9.13.
Suppose
{0j
:
j
=
l,2,...}
is an
orthogonal
sequence
in an
(infinite-dimensional)
inner product
space
V,
and f €
V.
Then
Proof.
By the
projection theorem,
for
each
JV,
is
the
element
of the
subspace
VN =
span
{</>i,
</>
2
,...,
0jv}
closest
to /, and
/AT
is
orthogonal
to /
—
/N.
Therefore,
by the
Pythagorean theorem,
This implies
that
Moreover,
since
0i,
</>2,
^>s,
• • • are
mutually orthogonal,
we
have (also
by the
Pythagorea
theorem)
JVf
n
Therefore,
holds
for
each
TV,
and the
result
follows.
Since
a
Fourier series
is
based
on an
orthogonal series, Bessel's inequality
can
be
applied
to the
sequence
of
Fourier
coefficients.
For
instance,
if
c
n
,
n
=
0,
±1,
±2,...
are the
complex Fourier
coefficients
of /
e
L
2
(—l,l),
then
and
Therefore,
428
Chapter
9.
More about Fourier
series
The next lemma
is
called Bessel's inequality and follows directly from the
projection theorem.
Lemma
9.13.
Suppose
{cPj
; j = 1,2,
...
} is
an
orthogonal sequence in an
{infinite-dimensional} inner product space
V,
and f E
V.
Then
Proof.
By the projection theorem, for each
N,
is
the element of
the
subspace V N = span {
cP1
,
cP2,
...
,
cP
N}
closest
to
f, and f N
is
orthogonal
to
f - f
N·
Therefore, by
the
Pythagorean theorem,
This implies
that
IlfNII~
::;
Ilfll~
for all N =
1,2,3,
....
Moreover, since
cP1,
c/>2,
cP3,
...
are mutually orthogonal,
we
have (also by the Pythagorea
theorem)
Therefore,
t l(f,
cPj)12
::;
Ilfll~
j=l
(cPj,
cPj)
holds for each
N,
and the result follows. 0
Since a Fourier series
is
based on an orthogonal series, Bessel's inequality
can be applied
to
the
sequence of Fourier coefficients. For instance, if en, n =
0,
±1,
±2,
...
are
the
complex Fourier coefficients of f E L2(
-f,
f), then
(I, ei7rnx/l)
and
Therefore,

9.4.
Pointwise
convergence
of
Fourier
series
429
Bessel's inequality yields
Similar results hold
for
Fourier sine
or
cosine
coefficients.
We
can now
state
and
prove
the
main result concerning
the
pointwise conver-
gence
of
Fourier series.
The
reader should note
that
the
convergence
of the
Fourier
series
is
naturally expressed
in
terms
of the
properties
of
f
per
rather
than
those
of
/•
Theorem
9.14.
Suppose
f
:
(—l,€)
-»
C is
piecewise
smooth. Then
the
complex
Fourier
series
of f,
converges
to
f
per
(x)
if
x is a
point
of
continuity
of
f
per
,
and to
if
fper
has a
jump discontinuity
atx.
Proof.
As
before,
we
write
If
f
per
is
continuous
at x,
then
From
now on, for
conciseness,
we
will
write
/
rather
than
f
per
and
remember
to
interpret
f(s)
in
terms
of the
periodic extension
of /
whenever
s is
outside
of the
infprval
f
—
P
t\
Alsn
-rarp
writ.p
With this understanding,
our
task
is to
show
that,
for
each
x G
[—f.,1],
To
do
this,
it
suffices
to
show
that
9.4. Pointwise convergence
of
Fourier
series
429
Bessel's inequality yields
00
n=-oo
Similar results hold for Fourier sine or cosine coefficients.
We
can now
state
and prove the main result concerning
the
pointwise conver-
gence of Fourier series. The reader should note
that
the
convergence of
the
Fourier
series
is
naturally expressed in terms of
the
properties of
fper
rather
than
those of
f·
Theorem
9.14.
Suppose f :
(-i,
i)
-+
C
is
piecewise smooth. Then the complex
Fourier series
of
f,
00
L
cnei1fnx/l,
n=-oo
converges
to fper(x)
if
x is a point
of
continuity of
fper,
and to
-2
1
[
lim fper(s) + lim
fper(S)]
s--+x - s--+x+
if
fper
has
a jump discontinuity at x.
Proof.
As
before,
we
write
N £
fN(X) = L
cnei1fnx/l
= 1
KN(S)f(x
-
s)
ds.
n=-N
-l
If
fper
is
continuous
at
x, then
fper(x) =
-2
1
[lim
fper(s) + lim
fper(X)]
.
s--+x-
s--+x+
From now on, for conciseness,
we
will write f rather
than
fper
and
remember
to
interpret
f(s)
in terms of the periodic extension of f whenever s
is
outside of the
interval
(-i,
i).
Also,
we
write
f(x-)
= lim f(s),
f(x+)
= lim f(s).
s--+x-
s--+x+
With this understanding, our task
is
to
show
that,
for each x E
[-i,i],
lim fN(X) =
~
[f(x-)
+
f(x+
)].
N--+oo 2
To
do this, it suffices to show
that
1
0 1
lim
KN(S)f(x
- s) ds = -
f(x+)
N--+oo
-l
2
(9.19)
430
Chapter
9.
More about Fourier
series
and
We
will
prove
that
(9.20)
holds;
the
proof
of
(9.19)
is
similar. Equation
(9.20)
is
eauivalent
to
By
(9.18),
so
We
can
recognize this integral
as
l/(2£)
times
the
L
2
inner product
(on the
interval
(0,£))
of the
functions
and
The
sequence
is
an
orthogonal sequence with respect
to the
L
2
inner product (see,
for
example,
Exercise
5.2.2).
Bessel's inequality
then
implies
that
and
therefore
This
is the
desired result.
However,
there
is one
problem with this argument. Bessel's inequality (Lemma
9.13) requires
that
F^
and the
orthogonal sequence belong
to a
common inner
product space.
We
will
take
this space
to be the
space
V of all
piecewise continuous
functions
defined
on
[0,£|.
Certainly
the
functions
430
Chapter
9.
More about Fourier
series
and
1
l 1
lim
KN(S)f(x
- s)
ds
=
-2
f
(x-).
N-+oo
0
(9.20)
We
will prove
that
(9.20) holds;
the
proof of (9.19)
is
similar. Equation (9.20)
is
equivalent to
By
(9.18),
1
fl ft
'2
f
(x-)
=
f(x-)
10
KN(S)
ds
=
10
KN(S)f(x-)
ds,
so
fl
KN(S)f(x
- s)
ds
- !
f(x-)
=
fl
KN(S)
(f(x
- s) -
f(x-))
ds
10
2
10
=
~
fl
f(x
- s)
~/(x-)
sin
((2N
+
l)7rS)
ds.
2i10
sin(u)
2i
We
can recognize this integral as 1/(2i) times
the
L2
inner product (on the interval
(0,
£))
of
the
functions
f(x-s)-f(x-)
F(x)(s)
= .
('IrS)
sm
2l
and
.
((2N
+
l)7rX)
sm 2i .
The sequence
{
.
((2N+l)11'X)
. N - 0 1 2 }
sln
2l
.
-",
...
is
an orthogonal sequence with respect to
the
L2
inner product (see, for example,
Exercise
5.2.2). Bessel's inequality then implies
that
~
1 ( .
((2N
+
l)7rS))
12
~o
F(x),sm
2i
<
00
and therefore
~
f1f(x-s)-f(x-).
((2N+1)7rs)d
_(D
.
((2N+1)7rS))
2£
10
sin
(~;)
sm
2l
s -
.l'(x),sm
2£
-t
O.
This
is
the desired result.
However, there
is
one problem with this argument. Bessel's inequality (Lemma
9.13) requires
that
F(x)
and
the
orthogonal sequence belong
to
a common inner
product space.
We
will take this space
to
be the space V of all piecewise continuous
functions defined on
[0,
£J.
Certainly
the
functions
.
((2N
+
l)7rX)
sm
2£
' N =
0,1,2,
...

9.4.
Pointwise
convergence
of
Fourier series
431
belong
to V
(continuous functions
are
piecewise continuous).
The
proof, therefore,
reduces
to
showing
that
F^
e
V.
Since
f
per
has
only jump discontinuities,
F(
x
)
also
has
only jump discontinu-
ities, except possibly
at s = 0,
where there
is a
zero
in the
denominator.
If we
show
that
exists
as a
finite
number, this will show
that
F^
is
piecewise continuous,
and
hence
in
V.
Since
/ and
df/dx
each
has at
most
a finite
number
of
jump discontinuities,
there
is an
interval
(0,e)
such
that
the
function
s
!->•
f(x
- s) is
continuous
and
differentiate
on
(0,e).
It
follows
from
the
mean value theorem
that,
for
each
s €
(0,e),
there exists
7
S
e
(0,1)
such
that
Also,
by the
mean value theorem, there exists
A
s
€
(0,1)
such
that
Thus,
for all s > 0
near zero,
we
have
This shows
that
lim
s
_>
0
+
F(
x
)(s)
exists, which completes
the
proof.
Example
9.15.
We
will
compute
the
complex
Fourier series
of g
:
[—1,1]
->
R
defined
by
g(x)
= x.
Figure 9.10 shows
thatg
per
is
piecewise smooth,
and
continuous
except
at
integral values
of
x. We
therefore
expect
that
the
Fourier series
of
g
will
converge
to
g
per
(x}
except
when
x is an
integer.
At the
points
of
discontinuity,
the
average
of the
left-
and
right-hand limits
is
0,
which
will
be the
limit
of the
series
at
those points.
The
Fourier
coefficients
of g are
9.4. Pointwise convergence
of
Fourier
series
431
belong
to
V (continuous functions are piecewise continuous).
The
proof, therefore,
reduces
to
showing
that
F(x)
E
V.
Since
fper
has only
jump
discontinuities,
F(x)
also has only
jump
discontinu-
ities, except possibly
at
s = 0, where there
is
a zero in
the
denominator.
If
we
show
that
lim F(x)(s)
s-+o+
exists as a finite number, this will show
that
F(x)
is piecewise continuous,
and
hence
in V. Since f
and
df / dx each has
at
most a finite number
of
jump
discontinuities,
there is
an
interval
(O,E)
such
that
the
function s
I-t
f(x
-
s)
is continuous
and
differentiable on
(0,
E).
It
follows from
the
mean value theorem
that,
for each s E
(O,E),
there exists IS E (0,1) such
that
df
f(x
-
s)
-
f(x-)
= - dx (x - fSS)S.
Also, by
the
mean value theorem, there exists
As
E (0,1) such
that
. (7rS) (AS7rs)
7rS
sm
2£
= cos U
2£
.
Thus, for all s > ° near zero,
we
have
f(x-s)-f(x-)
F(x)(s) = .
(1[8)
sm
2f
-1x(x
- ISS)S
=
--"""--':7"'-,---'--
cos
(>'.1[S)
1[S
2l
2f
1x(x - ISS)
cos
(>'o1[S).1!:..
2l
2£
~(x-)
-+
-
dx
as s
-+
0+
1[
.
2l
This shows
that
lims-+o+
F(:r;)(s)
exists, which completes
the
proof. 0
Example
9.15.
We will compute the complex Fourier series
of
9 :
[-1,1]
-+
R
defined
by
g(x) =
x.
Figure 9.10 shows that
gper
is piecewise smooth, and continuous
except at integral values
of
x.
We
therefore expect that the Fourier series
of
9 will
converge to gper(x) except when x is
an
integer.
At
the points
of
discontinuity, the
average
of
the left- and right-hand limits is 0, which will
be
the limit
of
the series
at those points.
The Fourier coefficients
of
9
are
Co
=
~
ill
X dx = 0,
111
.
i(-I)n
en = - xe-1[mx dx =
---,
n = ±1, ±2,
....
2
-1
n7r
432
Chapter
9.
More
about Fourier
series
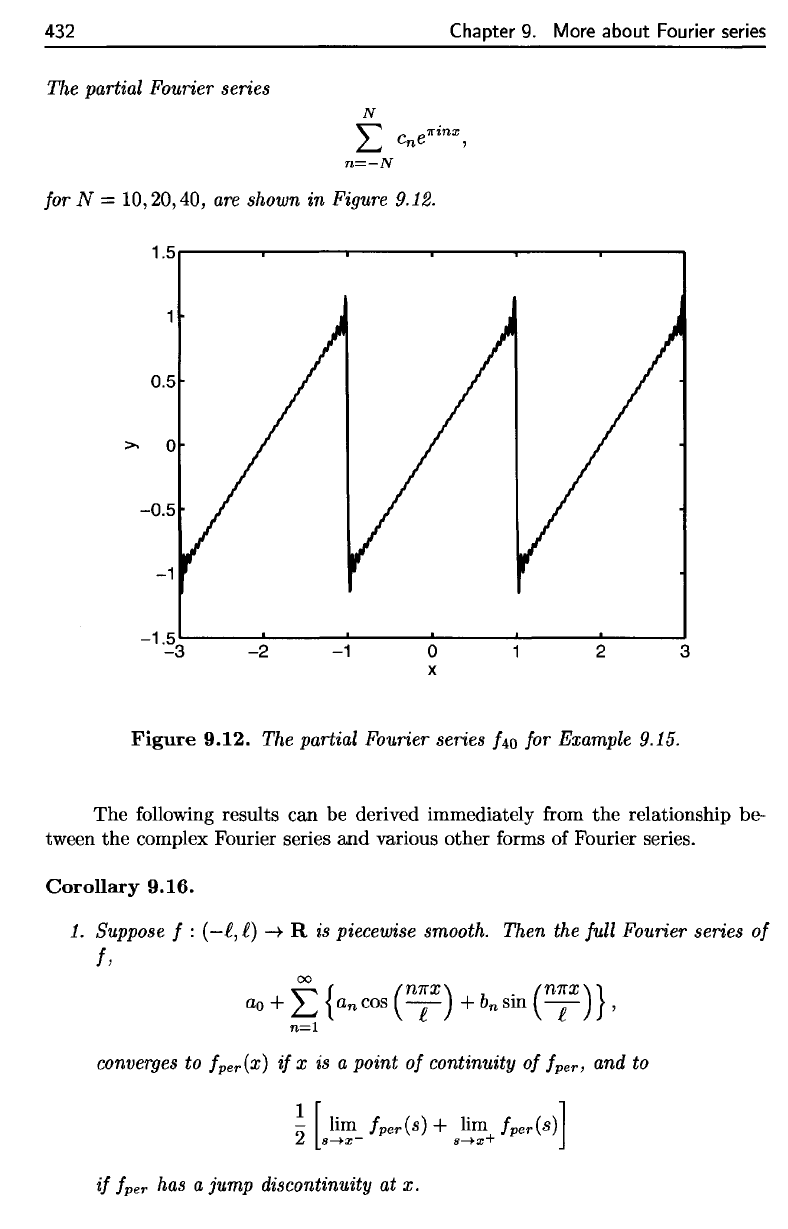
The
partial Fourier series
for
N =
10,20,40,
are
shown
in
Figure 9.12.
Figure
9.12.
The
partial Fourier series
/4o
for
Example 9.15.
The
following results
can be
derived immediately
from
the
relationship
be
tween
the
complex Fourier series
and
various other forms
of
Fourier series.
Corollary
9.16.
1.
Suppose
f
:
(—£,
i)
->
R is
piecewise
smooth. Then
the
full Fourier series
of
f,
converges
to
f
per
(x}
if
x is a
point
of
continuity
of
f
per
,
ana to
if
f
per
has a
jump discontinuity
atx.
432 Chapter 9. More
about
Fourier series
The
partial Fourier series
N
L c
n
e
7rin
",
n=-N
for N = 10,20,40,
are
shown in
Figure
9.12.
1.5~-----r------r------r------r------r----~
-1
.5
I..-
____
--L.
______
.L...-
____
--L.
______
.L...-
____
--L.
____
----l
-3
-2
-1 0 2 3
x
Figure
9.12.
The
partial Fourier series
f40
for Example
9.15.
The
following results
can
be derived immediately from
the
relationship be-
tween
the
complex Fourier series
and
various
other
forms
of
Fourier series.
Corollary
9.16.
1.
Suppose f :
(-I,
I)
-t
R
is
piecewise smooth. Then the full Fourier series
of
j,
converges
to
!per(x)
if
x
is
a point
of
continuity
of
fper,
and to
~
[lim
fper(s) +
lim
jper(s)]
2 s---+"-
s---+,,+
if
fper
has
a jump discontinuity at x.

9.4.
Pointwise
convergence
of
Fourier
series
433
2.
Suppose
f
:
(0,
t)
—>
R is
piecewise
smooth,
and let
f
0
dd
be the
periodic,
odd
extension
of
f to R
(that
is, the
periodic extension
to R
of
the odd
extension
°f
f
t°
(—£•>£))•
Then
the
Fourier sine series
of f,
converges
to
f
0
dd(%)
if
%
is
a
point
of
continuity
of
f
0
dd,
and to
if
fodd
has a
jump
discontinuity
at x.
3.
Suppose
f
:
(0,£)
—>
R is
piecewise smooth,
and let
f
ev
en
be the
periodic, even
extension
of
f
toU
(that
is, the
periodic extension
to R
of
the
even extension
of
f to
(—£,1)).
Then
the
Fourier cosine series
of f,
converges
to
f
e
ven(x)
if
x is a
point
of
continuity
of
f
even
,
and to
if
feven
has a
jump
discontinuity
atx.
Proof.
See
Exercise
6.
Example
9.17.
Let f
:
(0,1)
—>
R be
defined
by
f(x)
= 1.
Then
the
periodic,
odd
extension
of
f,
f
0
dd,
is
defined
by
(the
so-called
"square
wave"). Thus
f
0
dd
is
discontinuous
at
every integer value
of
x; at
those points
of
dicontinuities,
the
average
of the
left
and
right endpoints
is
zero. Figure 9.13 shows
f
0
dd
together with
its
partial sine series having
5, 10, 20,
and
40
terms.
As the
above
corollary
guarantees,
the
sine series converges
to f at
every
point
of
continuity (every nonintegral
point,
in
this
case)
and to
zero
at
every
point
of
discontinuity.
We
can
draw some further conclusions
from
Theorem 9.14
and
Corollary 9.16:
9.4. Pointwise convergence
of
Fourier series
433
2.
Suppose f : (0,
£)
-t
R is piecewise smooth, and let
fodd
be
the periodic, odd
extension
of
f to R (that is, the periodic extension to R
of
the odd extension
of
f to (-£,£)). Then the Fourier sine series
of
f,
00
L b
n
sin
(n;x),
n=l
converges to
fOdd(X)
if
x is a point
of
continuity
of
fodd' and to
if
fodd
has a
jump
discontinuity at
x.
3.
Suppose f : (0,
£)
-t
R is piecewise smooth, and let feven
be
the periodic, even
extension
of
f to R (that is, the periodic extension to R
of
the even extension
of
f to
(-£,
£)}.
Then the Fourier cosine series
of
f,
converges to leven(x)
if
x is a point
of
continuity
of
leven, and to
if
leven has a
jump
discontinuity at
x.
Proof.
See Exercise
6.
0
ExalTIple
9.17.
Let
I : (0,1)
-t
R
be
defined by
f(x)
= 1. Then the periodic, odd
extension
of
f,
lodd, is defined by
f
()
=
{1,
if
x E (2k,
2k
+
1)
(k an integer),
odd
x
-1,
if
x E (2k
-1,
2k) (k an integer)
(the so-called "square wave"). Thus
fodd
is discontinuous
at
every integer value
of
Xi
at those points
of
dicontinuities, the average
of
the left and right endpoints is
zero. Figure 9.13 shows lodd together with its partial sine series having
5,
10, 20,
and
40
terms.
As
the above corollary guarantees, the sine series converges to f at
every point
of
continuity (every nonintegral point,
in
this case) and to zero at every
point
of
discontinuity.
We
can draw some further conclusions from Theorem 9.14 and Corollary 9.16:
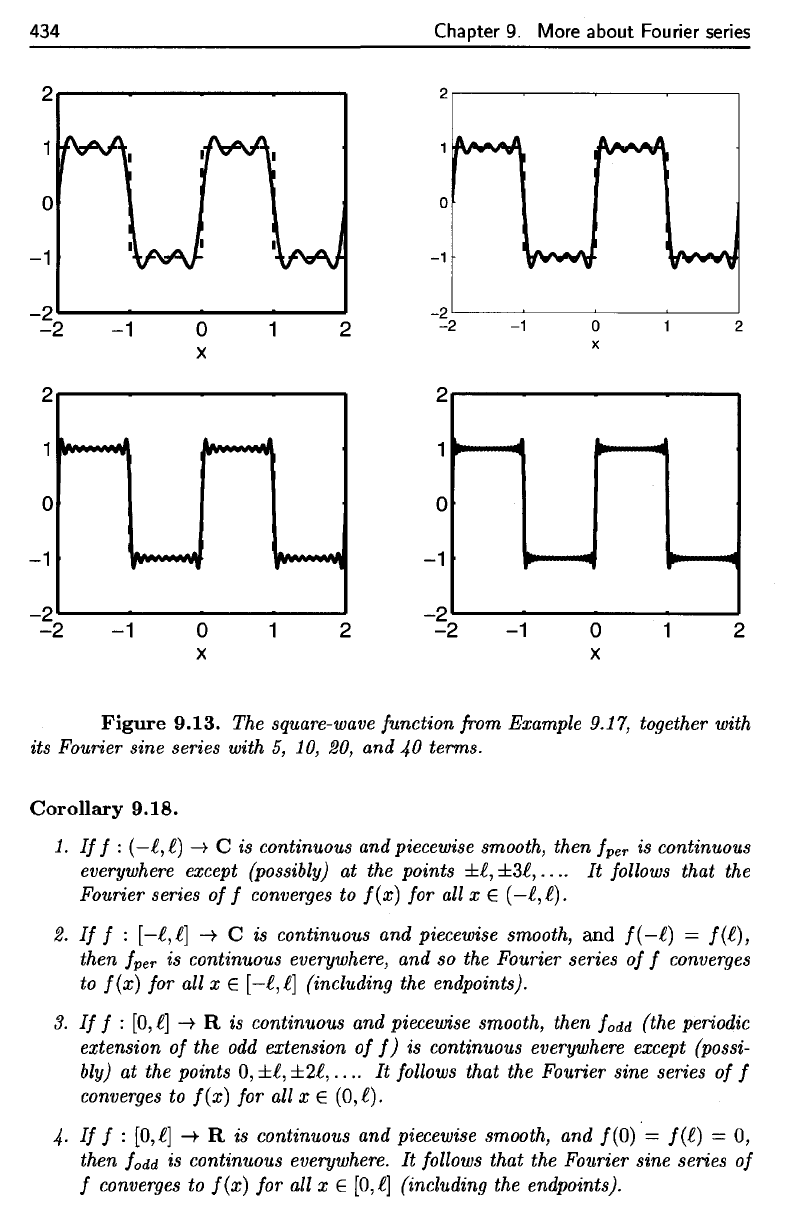
434
Chapter
9.
More about Fourier
series
Figure
9.13.
The
square-wave function from Example
9.17,
together with
its
Fourier sine series with
5, 10, 20, and 40
terms.
Corollary
9.18.
1.
If
f
:
(—£,£)
—>
C is
continuous
and
piecewise
smooth,
then
f
per
is
continuous
everywhere
except
(possibly)
at the
points
±£,±31,—
It
follows
that
the
Fourier
series
of
f
converges
to
f(x)
for all x €
(—i,i).
2. If f
:
[—t,£\
->•
C is
continuous
and
piecewise smooth,
and
f(—t]
=
f(l),
then
f
per
is
continuous everywhere,
and so the
Fourier series
of f
converges
to
f(x]
for all x €
[—•£,•£]
(including
the
endpoints).
3. If f
:
[0,1]
—>•
R is
continuous
and
piecewise smooth, then
f
0
dd
(the periodic
extension
of the odd
extension
of
f)
is
continuous everywhere
except
(possi-
bly)
at the
points
0,
±£,
±21,
— It
follows
that
the
Fourier sine series
of f
converges
to
f(x)
for all x
e
(0,^).
4-
If f '•
[0,^]
—>•
R is
continuous
and
piecewise smooth,
and
/(O)
=
f(i)
= 0,
then
f
0
dd
is
continuous everywhere.
It
follows
that
the
Fourier sine series
of
f
converges
to
f(x]
for all x €
[0,£]
(including
the
endpoints).
434
Chapter
9.
More about Fourier
series
2~------------------~
2
6
........
...A
06
.........
06
-
- - -
o
-1
A A A A
V
....
~
....
V
V
....
-
....
V
-1
-2
-2
-2
-1
o
X
1 2
-2
-1
o
x
2
2
2~------------------~
1
1
....
-
..
0 o
-1
-1
-2
-2~----------------~
-2
-1
o
x
1 2
-2
-1
o
x
1 2
Figure
9.13.
The
square-wave function from Example 9.17, together with
its Fourier sine series with
5,
10,
20,
and 40 terms.
Corollary
9.18.
1.
If
f :
(-f,
f)
~
C is continuous and piecewise smooth, then
fper
is continuous
everywhere except
{possibly}
at the points
±f,
±3f,
.
...
It
follows that the
Fourier series
of
f converges
to
f(x)
for
all
x E
(-f,
f).
2.
If
f :
[-f,f]
~
C is continuous and piecewise smooth,
and
f(
-f)
=
f(f),
then
fper
is continuous everywhere, and
so
the Fourier series
of
f converges
to
f(x)
for
all
x E
[-f,f]
{including the endpoints}.
3.
If
f :
[0,
f]
~
R is continuous and piecewise smooth, then
fodd
{the
periodic
extension
of
the
odd
extension
of
f}
is continuous everywhere except
{possi-
bly}
at the points 0,
±f,
±2£,
. ... It follows that the Fourier sine series of f
converges
to
f(x)
for
all
x E (O,f).
4·
If
f :
[O,f]
~
R is continuous and piecewise smooth, and
f(O)
=
f(f)
=
0,
then
fodd
is continuous everywhere. It follows that the Fourier sine series
of
f converges to
f(x)
for
all
x E
[0,£]
{including the endpoints}.

9.4. Pointwise
convergence
of
Fourier
series
435
5. If f
:
[0,
t]
—>•
R is
continuous
and
piecewise smooth, then
f
ev
en
(the periodic
extension
of
the
even extension
of
f)
is
continuous everywhere.
It
follows
that
the
Fourier cosine series
of f
converges
to
f(x)
for all x
G
[0,^]
(including
the
endpoints).
Proof.
The
conclusions
all
follow
directly
from
Corollary 9.16, except
for the
following:
If / :
[0,1]
—>
R is
continuous, then
f
even
is
continuous,
and
f
0
dd
is
continuous
provided
/(O)
—
f(i]
= 0. The
reader
is
asked
to
verify
these conclusions
in
Exercise
7. D
When
f
per
(or
f
0
dd,
or
feven)
is
continuous everywhere,
we can
draw
a
stronger
conclusion,
as we
show
in the
next section.
The
reader should
note
that,
from
the
point
of
view
of
approximating
a
given
function,
the
cosine series
is
more
powerful
than
the
sine series, since
f
even
is
continuous everywhere
for any
continuous
/ :
[Q,£]
-»
R.
Therefore,
for
example, Gibbs's phenomena cannot occur with
the
cosine series approximating such
a
function.
Exercises
1. Let / :
[-7r,7r]
->•
R be
defined
by
f(x)
=
x
3
.
Does
the
full
Fourier
series
of
/
converge (pointwise)
on R? If so,
what
is the
limit
of the
series?
2.
Define
/ :
[-2,2]
->•
R by
f(x]
=
x
3
+
1.
Write down
the
limits
of
(a)
the
Fourier
sine
series
of /
(regarded
as a
function defined
on
[0,2]),
(b)
the
Fourier cosine series
of /
(regarded
as a
function
defined
on
[0,2]),
and
(c)
the
full
Fourier series
of /.
3.
Find
an
example
of a
function
/ :
[0,1]
—>•
R
such
that
it is not the
case
that
the
Fourier cosine series
of /
converges
to / at
every
x €
[0,1].
4.
Using
the
original formula
for
KN,
prove
that
(9.18)
holds.
5.
Prove Theorem 9.8.
For
simplicity, assume
all of the
functions
are
continuous.
6.
Prove Corollary 9.16.
7.
Suppose
/
:
[0,1]
—>•
R is
continuous. Prove
that
feven
is
continuous every-
where,
and
that
if
/(O)
=
f(£)
— 0,
then
f
0
dd
is
continuous everywhere.
8. (a)
Extend Corollaries 9.16
and
9.18
to the
case
of the
quarter-wave
cosine
series.
(Hint:
see
Exercise
9.3.6.)
9.4. Pointwise convergence
of
Fourier
series
435
5.
If
f :
[0,
£]
-+ R
is
continuous and piecewise smooth, then
feven
(the periodic
extension of the even extension
of
f)
is
continuous everywhere. It
follows
that
the Fourier cosine series
of
f
converges
to
f(x)
for
all
x E
[0,£]
(including
the endpoints).
Proof.
The conclusions all
follow
directly from Corollary 9.16, except for the
following:
If
f :
[0,
£]
-+ R
is
continuous, then
feven
is
continuous, and
fodd
is
continuous provided
f(O)
= f(£) =
0.
The reader
is
asked to verify these conclusions
in Exercise
7.
D
When
fper
(or
fodd,
or
feven)
is
continuous everywhere,
we
can draw a stronger
conclusion, as
we
show in
the
next section. The reader should note
that,
from the
point of view of approximating a given function, the cosine series
is
more powerful
than
the
sine series, since
feven
is
continuous everywhere for any continuous f :
[0,
£]
-+
R.
Therefore, for example, Gibbs's phenomena cannot occur with the
cosine series approximating such a function.
Exercises
1.
Let
f:
[-1f,1f]-+ R be defined by
f(x)
= x
3
.
Does
the
full Fourier series of
f converge (pointwise) on
R?
If
so, what
is
the limit of the series?
2.
Define f :
[-2,2]-+
R by
f(x)
= x
3
+
1.
Write down
the
limits of
(a) the Fourier sine series of
f (regarded as a function defined on [0,2]),
(b) the Fourier cosine series of
f (regarded as a function defined on [0,2]),
and
( c ) the full Fourier series of
f.
3.
Find an example of a function f :
[0,
1]
-+ R such
that
it
is
not the case
that
the Fourier cosine series of 1 converges to 1
at
every x E
[0,
1].
4.
Using
the
original formula for K
N
,
N
K
(())
=
~
"'"
ei1fnO/l
N
2£
~
,
n=-N
prove
that
(9.18) holds.
5.
Prove Theorem 9.8. For simplicity, assume all of the functions are continuous.
6.
Prove Corollary 9.16.
7.
Suppose f :
[0,
£]
-+ R
is
continuous. Prove
that
feven
is
continuous every-
where, and
that
if 1(0) = f(£) =
0,
then
lodd
is
continuous everywhere.
8.
(a) Extend Corollaries 9.16 and 9.18 to
the
case of
the
quarter-wave cosine
series. (Hint: see Exercise 9.3.6.)

436
Chapter
9.
More about Fourier
series
(b)
Define
/ :
[0,1]
->
R by
f(x]
= 1 + x. To
what function does
the
quarter-wave cosine series
of /
converge?
9.
(a)
Extend Corollaries 9.16
and
9.18
to the
case
of the
quarter-wave
sine
series. (Hint:
see
Exercise 9.3.5.)
(b)
Define
/ :
[0,1]
—>
R by
f(x]
= 1 + x. To
what function does
the
quarter-wave
sine series
of /
converge?
9.5
Uniform convergence
of
Fourier
series
In the
previous section,
we
proved
the
pointwise convergence
of the
Fourier series
of
a
piecewise smooth function.
We
will
now
consider conditions under which
the
convergence
is
actually
uniform.
The
property
of
uniform convergence
is
very
de-
sirable, since
it
implies
that
a finite
number
of
terms
from
the
Fourier series
can
approximate
the
function
accurately
on the
entire interval;
in
particular,
uniform
convergence
rules
out the
possibility
of
Gibbs's
phenomenon, which
was
introduced
in
Section 5.2.2
and
will
be
discussed
further
below.
The
rapidity
with which
a
Fourier series converges, and,
in
particular,
whether
it
converges
uniformly
or
not,
is
intimately related
to the
rate
at
which
its
coefficients
converge
to
zero.
We
address this question
first.
9.5.1 Rate
of
decay
of
Fourier coefficients
In
the
following
theorems,
we
will
show
that
the
Fourier
coefficients
c
n
,
n
=
0,±1,±2,...,
of/
satisfy
where
the
exponent
k is
determined
by the
degree
of
smoothness
of /.
Recall
that
(9.21)
means
that
there
is a
constant
M > 0
such
that
The
same condition
that
guarantees pointwise convergence
of
Fourier series
also ensures
that that
the
Fourier
coefficients
decay—converge
to
zero—at
least
as
fast
as
1/n,
n
=
1,2,3,
—
Theorem
9.19.
Suppose
that
f
:
(—£,1)
->
C is
piecewise smooth,
and let
c
n
,
n = 0, ±1,
±2,...,
be the
complex
Fourier
coefficients
of
f.
Then
Proof.
Since
/ is
piecewise smooth, there
are a finite
number
of
discontinuities
of
/
and/or
df/dx.
We
label these points
as
436
Chapter
9.
More
about
Fourier series
(b) Define f : [0,1]
-+
R by
f(x)
= 1 +
x.
To what function does
the
quarter-wave cosine series of f converge?
9.
(a) Extend Corollaries 9.16
and
9.18
to
the case of the quarter-wave sine
series. (Hint: see Exercise 9.3.5.)
(b) Define
f : [0,1]
-+
R by
f(x)
= 1 +
x.
To what function does the
quarter-wave sine series of
f converge?
9.5 Uniform convergence
of
Fourier
series
In
the
previous section,
we
proved
the
pointwise convergence of
the
Fourier series
of a piecewise smooth function.
We
will now consider conditions under which the
convergence
is
actually uniform. The property of uniform convergence
is
very de-
sirable, since it implies
that
a finite number of terms from the Fourier series can
approximate
the
function accurately on
the
entire interval; in particular, uniform
convergence rules out the possibility of Gibbs's phenomenon, which was introduced
in Section 5.2.2 and will be discussed further below.
The rapidity with which a Fourier series converges, and, in particular, whether
it converges uniformly or not,
is
intimately related
to
the
rate
at
which its coefficients
converge
to
zero.
We
address this question first.
9.5.1 Rate of
decay
of Fourier coefficients
In the following theorems,
we
will show
that
the Fourier coefficients C
n
,
n =
0,
±1, ±2,
...
, of f satisfy
(9.21)
where
the
exponent k
is
determined by
the
degree of smoothness of f. Recall
that
(9.21) means
that
there
is
a constant M > 0 such
that
M
Icnl
:::;
Inlk
for all
n.
The same condition
that
guarantees pointwise convergence of Fourier series
also ensures
that that
the Fourier coefficients
decay-converge
to
zero-at
least as
fast as
l/n,
n =
1,2,3,
....
Theorem
9.19.
Suppose that f :
(-£,
£)
-+
C is piecewise smooth, and let en,
n = 0,
±1,
±2,
...
,
be
the complex Fourier coefficients
of
f.
Then
Proof. Since f
is
piecewise smooth, there are a finite number of discontinuities of
f
and/or
dfldx.
We
label these points as
-£
<
Xl
<
X2
< ... <
Xm-l
< £

9.5. Uniform convergence
of
Fourier
series
437
and
write
XQ
—
—t,
x
m
= t. We
then have
It
then
suffices
to
show
that,
for
each
j =
1,2,...,
m,
Since
/ is
continuously
differentiable
on
(xj-i,Xj),
and the
limits
of
both
/ and
df/dx
exist
at the
endpoints
of
this interval,
we can
apply integration
by
parts
to
obtain
Since
each
of
these three terms
is
bounded
by a
constant times
l/|n|,
the
result
follows.
We
have used
the
fact
that
/ and
df/dx,
being piecewise continuous,
are
both bounded
on
(—1,1).
When
/ has
some additional smoothness,
its
Fourier
coefficients
can be
shown
to
decay more rapidly.
Theorem
9.20.
Suppose
f
:
(—(.,£)
—>•
C has the
property
that
its
periodic exten-
sion
f
per
and the first k — 2
derivatives
of
f
per
are
continuous,
where
k
>2,
and
the (k —
l)st
derivative
of
f is
piecewise
smooth.
If
c
n
,
n
= 0, ±1,
±2,...,
are the
complex
Fourier
coefficients
of f,
then
In
particular,
if
f
per
is
continuous
and its
derivative
is
piecewise
smooth, then
Proof.
Suppose
f
per
is
continuous
and
df/dx
is
piecewise smooth. Then,
by
inte-
gration
by
parts,
we
have
9.5. Uniform convergence
of
Fourier
series
and write
Xo
=
-e,
xm =
e.
We
then have
C
n
=
;e
[ff
!(x)e-i7rnx/f dx
=
~
f=
i
X
;
f(x)e-
i7rnx
/£
dx.
21!
j=l
X;-1
It
then
suffices
to
show
that,
for each j = 1,2,
...
, m,
i
x
; f(x)e-i7rnx/£ dx
= 0
(~)
.
X;-1
Inl
437
Since f is continuously differentiable on
(x
j
-1
, X j
),
and
the
limits of both f and
df
/ dx exist
at
the endpoints of this interval,
we
can apply integration by
parts
to
obtain
f(x)e-
i7rnx
/£
dx =
f(x)
e .
__
z_
_(x)e-
i7rnx
/£
dx
i
x
; [ -i7rnx/£]
x;
'e
i
X
;
df
X;_1
-z7fn/e
X;_1
7fn
X;-1
dx
=
!!...
(!(x,
-
)e-
i7rnx
;/f
-
f(x
'-1
+
)e-
i7rnX
;_l/f)
n7f J J
ie i
X
; df ( ) -i7rnx/f d
--
- x e
x.
7fn
X;_1
dx
Since each of these three terms
is
bounded by a constant times l/lnl,
the
result
follows.
We
have used
the
fact
that!
and
df
/dx,
being piecewise continuous, are
both
bounded on
(-e,
e).
0
When
f has some additional smoothness, its Fourier coefficients can be shown
to decay more rapidly.
Theorem
9.20.
Suppose f :
(-e,
e)
-+
C has the property that its periodic exten-
sion
fper
and the first k - 2 derivatives
of
fper
are
continuous, where k
~
2, and
the (k -
l)st
derivative
of
f
is
piecewise smooth.
If
Cn,
n =
0,
±1, ±2,
...
,
are
the
complex Fourier coefficients
of
f,
then
In particular,
if
fper
is
continuous and its derivative is piecewise smooth, then
Proof.
Suppose
fper
is
continuous and
df
/ dx
is
piecewise smooth. Then, by inte-
gration by parts,
we
have
f(x)e-i7rnx/f dx =
f(x)
e .
__
z
_(x)e-
i7rnx
/£
dx
I
t
[-i7rnX/t]f
'e
1£
dlf
_£
-Z7fn/e
-t
7fn
-f
dx
