Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


408
Chapter
9.
More
about
Fourier
series
Using
the
above
results,
we can
devise
an
efficient
algorithm
for
solving
(ap-
proximately)
the BVP
(9.4):
1.
Using
the
FFT,
estimate
the
Fourier coefficients
d-w,d-N+i,
• •
•,djv-i
of /.
2.
Use
(9.6)
to
estimate
the
corresponding Fourier series
of the
solution
u.
3. Use the
inverse
FFT to
estimate
the
values
of
u on the
grid
—i,
—l+h,...,
i—h,
h
=
t/N.
Example
9.4.
We use the
above
algorithm
to
estimate
the
solution
of
The
forcing function
f(x]
= x
3
satisfies
the
compatibility
condition,
as can
easily
be
verified.
An
exact solution
is
u(x)
= (x
—
x
5
)/2Q,
which corresponds
to
choosing
CQ
= 0 in the
Fourier series
We
will
use N = 128 =
2
7
;
which makes
the FFT
particularly
efficient.
Using
(9.8),
implemented
by the
FFT,
we
produce
the
estimates
(Recall
the
/_i28
i$
taken
as the
average
of
f(—1)
and
/(I);
in
this case, this aver-
age
is
0.)
To
indicate accuracy
of the
computed Fourier
coefficients,
we
graph
the
logarithm
of
the
absolute error
in the
resulting trigonometric interpolating function
I(x],
as
given
by
(9.11),
in
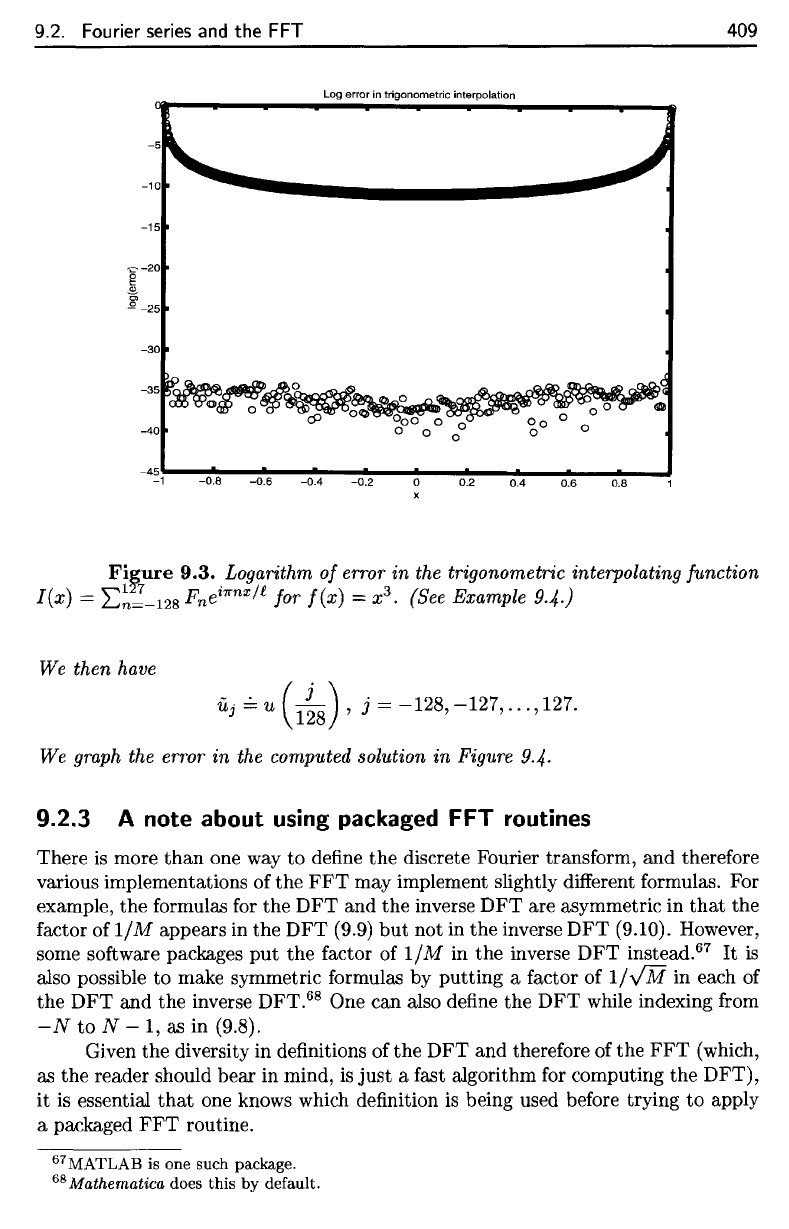
Figure
9.3.
As
this
graph
shows,
the
error
is
essentially
zero
at the
interpolation nodes
and
very small
in
between,
except
near
the
endpoints
where
Gibbs's
phenomenon
is
evident
(because
f is not
periodic).
(We
graph
the
logarithm
of the
error
because
of the
great disparity
in the
magnitude
of the
error
near
the
endpoints
and in the
interior
of the
interval.
If
we
graphed
the
error
itself,
only
the
Gibbs's
phenomenon
would
be
discernible
on the
scale
of the
graph.)
We
next compute
the
estimates
0/c_i28,C-i27
5
...
,0127.'
and
we
take
c$
— 0.
Finally,
we use the
inverse
FFT to
produce
the
estimates
408
Chapter
9.
More about Fourier series
Using the above results,
we
can devise
an
efficient algorithm for solving (ap-
proximately) the
BVP
(9.4):
1.
Using
the
FFT,
estimate
the
Fourier coefficients
d-N,
d_
N +1 ,
...
,
dN
-1
of f.
2.
Use (9.6)
to
estimate the corresponding Fourier series of the solution u.
3. Use the inverse
FFT
to
estimate the values of u on
the
grid
-i,
-i+h,
... ,
i-h,
h =
iiN.
Example
9.4.
We use the
above
algorithm to estimate the solution
of
d
2
u
- - = x
3
-1
< x < 1
dx
2
' - ,
u(
-1)
=
u(l),
du
(-1)
= du (1).
dx dx
(9.14)
The forcing function
f(x)
= x
3
satisfies the compatibility condition,
as
can easily
be
verified.
An
exact solution is
u(x)
=
(x
- x
5
)/20, which corresponds to choosing
Co
= 0
in
the Fourier series
00
u(x)
= L c
n
e
i
7l'nx.
n=-oo
We will use N =
128
= 2
7
, which makes the
FFT
particularly efficient. Using
(9.8), implemented by the FFT,
we
produce the estimates
(Recall the f-128 is taken
as
the average
of
f(-l)
and
f(l);
in
this case, this aver-
age
is 0.)
To
indicate accuracy
of
the computed Fourier coefficients,
we
graph the
logarithm
of
the absolute error
in
the resulting trigonometric interpolating function
I(x),
as
given by (9.11),
in
Figure 9.3.
As
this graph shows, the error is essentially
zero at the interpolation nodes and very small
in
between, except near the endpoints
where Gibbs's phenomenon is evident (because f is
not
periodic).
(We
graph the
logarithm
of
the error because
of
the great disparity
in
the magnitude
of
the error
near the endpoints and
in
the interior
of
the interval.
If
we
graphed the error itself,
only the Gibbs's phenomenon would
be
discernible on the scale
of
the graph.)
We
next
compute the estimates
of
C-128,
C-127,
...
,C127:
_ Fn
Cj
=
22'
n =
±1,±2,
...
,
n7f
and we take
Co
=
O.
Finally,
we
use the inverse
FFT
to produce the estimates
127
- . -
'"'"
-
i7l'jn/N
. -
-128 -127
127
u
J
-
~
cne , J - , ,
...
, .
n=-128
9.2. Fourier
series
and the FFT
409
Figure
9.3. Logarithm
of
error
in the
trigonometric interpolating function
We
then have
9.2.3
A
note
about
using
packaged
FFT
routines
There
is
more
than
one way to
define
the
discrete Fourier transform,
and
therefore
various implementations
of the FFT may
implement slightly
different
formulas.
For
example,
the
formulas
for the DFT and the
inverse
DFT are
asymmetric
in
that
the
factor
of 1/M
appears
in the DFT
(9.9)
but not in the
inverse
DFT
(9.10). However,
some software packages
put the
factor
of 1/M in the
inverse
DFT
instead.
67
It is
also possible
to
make symmetric formulas
by
putting
a
factor
of
1/vM
in
each
of
the DFT and the
inverse
DFT.
68
One can
also
define
the DFT
while indexing
from
-N to N - 1, as in
(9.8).
Given
the
diversity
in
definitions
of the DFT and
therefore
of the FFT
(which,
as the
reader
should
bear
in
mind,
is
just
a
fast
algorithm
for
computing
the
DFT),
it is
essential
that
one
knows which definition
is
being used before trying
to
apply
a
packaged
FFT
routine.
67
MATLAB
is one
such package.
68
Mathematica
does
this
by
default.
We
graph
the
error
in the
computed solution
in
Figure
9-4-
9.2. Fourier
series
and
the FFT
409
Log error in trigonometric interpolation
-15
-.:--20
g
-5;
..Q
-25
-30
-4~~1
---~0.8::-----:-0:-::.6---~0.~4
--:-0~.2:----:0~-~0.2~~0~.4-~0.~6
--:0~.8:--"""
Fi~ure
9.3.
Logarithm
of
error
in
the trigonometric interpolating function
I(x)
=
2:~~-128
Fnei1rnx/f for
f(x)
= x
3
.
(See Example 9.4.)
We then have
Uj
==
u
C;8)
, j = -128, -127,
...
,127.
We graph the error
in
the computed solution
in
Figure 9.4.
9.2.3 A
note
about
using packaged
FFT
routines
There
is
more
than
one way
to
define
the
discrete Fourier transform,
and
therefore
various implementations of
the
FFT
may implement slightly different formulas. For
example,
the
formulas for
the
DFT
and
the
inverse
DFT
are asymmetric in
that
the
factor of
11M
appears in
the
DFT
(9.9)
but
not
in
the
inverse
DFT
(9.10). However,
some software packages
put
the
factor of
11M
in
the
inverse
DFT
instead.
67
It
is
also possible
to
make symmetric formulas by
putting
a factor of
1/VM
in each of
the
DFT
and
the
inverse DFT.68 One can also define
the
DFT
while indexing from
-N
to
N -
1,
as
in (9.8).
Given
the
diversity in definitions of
the
DFT
and
therefore of
the
FFT
(which,
as
the
reader should bear in mind, is
just
a fast algorithm for computing
the
DFT),
it
is essential
that
one knows which definition is being used before trying
to
apply
a packaged
FFT
routine.
57MATLAB is one such package.
58
Mathematica
does
this
by
default.

410
Chapter
9.
More about Fourier
series
Figure
9.4. Error
in
computed
solution
in
Example
9.4-
It can be
shown
that
the DST is its own
inverse,
up to a
multiplicative
constant:
applying
the DST to
F
0
,FI,
...,
FN-I
produces
the
original
sequence
multiplied
by
27V
(see Exercise
9).
In
solving
a BVP or an
IBVP
with Dirichlet conditions,
the
main calculations
are:
1.
computing
the
Fourier sine
coefficients
of a
given
function;
2.
computing
the
solution
from
its
Fourier
coefficients.
9.2.4 Fast transforms
and
other
boundary
conditions;
the
discrete
sine transform
Fast
transform methods
are not
restricted
to
problems with periodic boundary
conditions.
Discrete
transforms
can be
defined
that
are
useful
for
working with
sine, cosine, quarter-wave sine,
and
quarter-wave cosine series,
as
well
as
with
the
full
Fourier series.
A
comprehensive source
of
software
for the
corresponding fast
transforms
is
[48].
As
an
example,
we
discuss
the
discrete sine transform (DST)
and its use in
solving
problems with Dirichlet conditions.
The DST of a
sequence
/i,
/2,
• •
•,
/AT-I
is
defined
by
410 Chapter 9. More
about
Fourier series
Error in computed solution
-1~--------~----------~--------~--------~
-1
-0.5
0
0.5
x
Figure
9.4.
Error
in
computed solution
in
Example 9.4.
9.2.4 Fast transforms
and
other boundary conditions; the
discrete
sine
transform
Fast transform methods are not restricted to problems with periodic boundary
conditions. Discrete transforms can
be
defined
that
are useful for working with
sine, cosine, quarter-wave sine, and quarter-wave cosine series, as well as with the
full Fourier series. A comprehensive source
of
software for the corresponding fast
transforms
is
[48].
As
an
example,
we
discuss the discrete sine transform (DST)
and
its use in
solving problems with Dirichlet conditions.
The
DST of a sequence ft,
12,
.. ·,
!N-1
is defined by
N-1
(.)
Fn
= 2
~
Ii
sin
7r;J
,n
=
0,1,
...
,N
- 1.
)=1
(9.15)
It
can
be
shown
that
the
DST
is
its own inverse, up to a multiplicative constant:
applying
the
DST
to
F
o
,
F
1
,
••.
, F N
-1
produces the original sequence multiplied by
2N
(see Exercise 9).
In
solving a
BVP
or
an
IBVP with Dirichlet conditions, the main calculations
are:
1. computing the Fourier sine coefficients of a given function;
2.
computing the solution from its Fourier coefficients.

Using
the
regular grid
Xj =
jh,
j —
0,1,2,...,
A/",
h =
t/N,
and the
trapezoidal
rule,
we
obtain
and we see
that
u can be
estimated
on a
regular grid
by
another application
of the
DST.
9.2.5 Computing
the DST
using
the FFT
As
mentioned above, there
are
special programs available
for
computing transforms,
such
as the
DST, using
FFT-like
algorithms. However, these programs
are
more
specialized
and
therefore less widely available
than
the
FFT.
69
Fortunately,
the
DST
can be
computed using
the DFT
(and hence
the
FFT)
and a few
additional
manipulations.
We
will
now
explain
how to do
this.
69
For
example, MATLAB
has an FFT
command,
but no
fast
DST
command.
9.2. Fourier
series
and the FFT
411
As
with
the DFT and
complex Fourier series,
we can
solve these problems approx-
imately using
the
DST.
If /
e
(?[(),£],
then
the
Fourier sine
coefficients
of / are
cnvpn
V>v
where
fj =
f(xj).
The
trapezoidal rule
simplifies
due to the
fact
that
sin(O)
=
sin
(n?r)
= 0. We
therefore
see
that
the
approximate Fourier sine
coefficients
are
just
a
multiple
of the DST of the
sequence
/(#i),
/(a^),
••••>
f(%N-i)-
On
the
other hand, suppose
the
Fourier sine series
of u is
and we
know
Ci,C2,.
-.,
cjv-i
(or
approximations
to
them).
We
then have,
for
j
=
l,2,...,JV-l,
9.2. Fourier
series
and
the FFT
411
As
with
the
DFT
and complex Fourier series,
we
can solve these problems approx-
imately using
the
DST.
If
f E
e[O,
el,
then the Fourier sine coefficients of f are
given by
2 {l
(n7rX)
cn=eJo
f(x)sin
-e- dx,
n=1,2,3,
....
Using the regular grid
Xj
=
jh,
j =
0,1,2,
...
,
N,
h =
elN,
and
the
trapezoidal
rule,
we
obtain
N-1
.
2"
(
).
(n7rXj)
en = C
~
f
Xj
sm
-e-
h
j=1
where
fJ
=
f(xj).
The trapezoidal rule simplifies due
to
the fact
that
sin
(0)
sin
(n7r)
=
O.
We
therefore see
that
the
approximate Fourier sine coefficients are
just
a multiple of the DST of the sequence
f(xd,
f(X2),
...
,
f(XN-d.
On the other hand, suppose the Fourier sine series of u
is
00
u(x)
= L C
n
sin
(n;x)
n=1
and
we
know
C1, C2,
.•.
, C N
-1
(or approximations to them).
We
then have, for
j = 1,2,
...
, N -
1,
N-l
(
)
."
.
(n7rXj)
u
Xj
=
~
C
n
sm
-e-
n=1
.
7rnJ
N-l
(.)
=
~Cnsm
N '
and
we
see
that
u can be estimated on a regular grid by another application of
the
DST.
9.2.5 Computing the DST
using
the FFT
As
mentioned above, there are special programs available for computing transforms,
such as
the
DST, using FFT-like algorithms. However, these programs are more
specialized and therefore less widely available
than
the FFT.69 Fortunately,
the
DST can be computed using the
DFT
(and hence
the
FFT)
and a
few
additional
manipulations.
We
will now explain how
to
do this.
69For example, MATLAB
has
an
FFT
command,
but
no fast
DST
command.
412
Chapter
9.
More
about Fourier
series
We
assume
that
{fj}f
=l
l
is a
sequence
of
real numbers
and
that
we
wish
to
compute
the DST of
{fj}.
We
define
a new
sequence
{fj}™^
1
by
We
then
define
{F
n
}
2
^
to be the DFT of
{fj}:
Since
we are
interested
in the
DST,
we
will look
at the
imaginary
part
of
F
n
,
which
is
(using
the
fact
that
/
0
=
/AT
= 0)
(using
the
fact
that
fj+N
=
/ZN-N-J
=
/N-J
for j =
1,2,...,
TV
—
1).
We
have
and so
It
follows
that
the
sequence
412
Chapter
9.
More about Fourier
series
We
assume
that
{Ii
}f=11
is a sequence of real numbers
and
that
we
wish
to
compute
the
DST
of
{Ii}.
We
define a new sequence
{ij}~:0-1
by
{
Ij,
j=1,2,
...
,N-1,
h=
-hN-j,
~=N+1,N+2,
...
,2N-1,
0, J =
O,N.
2N-1
Fn
=
2~
L he-1rijnIN
j=O
1
2N-1
(.)
.
2N-1
(.
)
-
7rJn
z
-.
7rJn
=
2N
?=
Ii
cos N -
2N
L
fJ
sm N .
J~ J~
Since
we
are interested in
the
DST,
we
will look
at
the
imaginary
part
of
Fn,
which
is (using
the
fact
that
}o
=
}N
= 0)
2N-1
(.
)
- 1 -
7rJn
Im(Fn) = -
2N
?=
Ii
sin N
J=O
= _
2~
{~}j
sin
(7r~n)
+
2f1
}j
sin
(7r~n)}
}=o
J=N+l
~-2~
{X;fjsm(~tn)
-
X;fN_jSin(~(j~N)n)}
(using
the
fact
that
jJ+N
=
hN-N-j
=
IN-j
for j =
1,2,
...
, N - 1).
We
have
~
I . 7r(j +
N)n
~
I.
7r
2N
-
j)n
N-1
( )
N-1
( ( )
-
L.....-
N-j
sm
N = -
L.....-
j sm N
j=1 j=1
N-1
( . )
= - L
Ij
sin
2n7r
_
7r~n
3=1
N-l
(.
)
=
?=
Ij
sin
7r~n
,
J=1
and
so
Im(Fn)
~
-
2~
{
2
X;
/;
sin (
~tn)
} .
It
follows
that
the
sequence

9.2. Fourier
series
and the FFT
413
is the DST of
{/_,-}.
The
reader should note
that,
when using
the FFT to
compute
the
DST,
N
should
be a
product
of
small primes
for
efficiency.
A
similar technique allows
one to
compute
the
discrete cosine transform (DCT)
using
the
FFT.
The DCT is
explored
in
Exercise
10.
Exercises
1.
Define
a
sequence
{fj}}=
0
by
Compute
the DFT
{F
n
}
of
{fj}
and
graph
its
magnitude.
2.
Let / :
[—7r,7r]
—>
R be
defined
by
/(#)
=
x
2
.
Use the DFT to
estimate
the
complex
Fourier
coefficients
c
n
of /,
n
=
—8,—7,...,7.
Compare with
the
exact values:
CQ
—
7r
2
/3,
c
n
=
2(—l)
n
/n
2
,
n = ±1, ±2, —
3.
Let / :
[—1,1]
^
R be
defined
by
f(x)
=
x(l
-
x
2
}.
The
complex Fourier
coefficients
of / are
Use
the
inverse
DFT to
estimate
/ on a
grid,
and
graph both
/ and the
computed
estimate
on
[—1,1].
Use
c_ie,
c_i5,...,
Ci5.
4.
Show
that,
with
/
defined
by
(9.11),
the
interpolation equations (9.12)
and
(9.13) hold.
5.
Let
ao,
«i,...,
CLN-I
be a
sequence
of
real
or
complex numbers,
and
define
Prove
that
Hint: Substitute
the
formula
for
A
n
into
and
interchange
the
order
of
summation.
(A
dummy index,
say
m,
must
be
used
in
place
of j in the
formula
for
A
n
.)
Look
for a
geometric series
and use
9.2. Fourier series and
the
FFT
413
is
the
DST of {lj}.
The reader should note
that,
when using the
FFT
to
compute
the
DST, N
should be a product of small primes for efficiency.
A similar technique allows one
to
compute the discrete cosine transform (DCT)
using
the
FFT.
The DCT
is
explored in Exercise
10.
Exercises
1. Define a sequence
{Ii
g~o
by
f
.
(37r
j
)
j = sm
10
.
Compute
the
DFT
{Fn}
of
{Ii}
and graph its magnitude.
2.
Let f :
[-7r,7r]
-+
R be defined by
f(x)
= x
2
•
Use the
DFT
to estimate the
complex Fourier coefficients
C
n
of f, n =
-8, -7,
...
,7. Compare with the
exact values:
Co
=
7r
2
/3, C
n
=
2(
-I)n
/n
2
,
n =
±I,
±2,
....
3.
Let f :
[-1,1]
-+
R be defined by f(x) =
x(I
- x
2
).
The complex Fourier
coefficients of
f are
6i(
-I)n
Co
=
0,
C
n
= 3 3 ' n =
±I,
±2,
....
n7r
Use the inverse
DFT
to estimate f on a grid,
and
graph
both
f and
the
computed estimate on
[-1,1].
Use
C-16,
C-15,·
..
,
C15.
4.
Show
that,
with I defined by (9.11),
the
interpolation equations (9.12) and
(9.13) hold.
5.
Let ao,
aI,
...
,
aN
-1
be a sequence of real or complex numbers,
and
define
Prove
that
N-l
A
=
~
" a
'e-21Tinj/N
0 1 N 1
n
N~J
,n="
...
,-.
j=O
N-l
. -
"A
21Tinj / N . - 0 1 N - 1
a
J
-
~
n
e
,
J - , ,
...
, .
n=O
Hint: Substitute the formula for
An
into
N-l
L
Ane21Tinj/N
n=O
and interchange the order of summation.
(A
dummy index, say m, must be
used in place of
j in the formula for
An.)
Look for a geometric series and use
~
rn = r
K
+
1
-
1.
~
r-I
n=O

414
Chapter
9.
More about Fourier
series
6.
Suppose
u
satisfies periodic boundary conditions
on the
interval
[—•£,•£],
and
is
the
complex Fourier series
of u.
Prove
that
Show
that
QJ
=
2JV/j,
j =
0,1,...,
N
—
I.
Hint: Proceed according
to the
hint
in
Exercise
5. You can use the
fact
that
the
vectors
are
orthogonal
in
R
N
l
for
j,
m
=
1,2,...,
N
—
l,j^m
(see Exercise 3.5.7).
Also,
each
of
these vectors
has
norm
\/N/1
(see Exercise 9.1.7).
10.
The
DOT
maps
a
sequence
{fj}^
=0
of
real numbers
to the
sequence
{F
n
}^
=0
,
where
is
the
complex Fourier series
of
—d?u/dx
2
.
7.
Use the DST to
estimate
the first 15
Fourier
coefficients
of the
function
f(x}
=
x(l
—
x) on the
interval
[0,1].
Compare
to the
exact values
8. The
Fourier sine
coefficients
of
f(x)
= x(l
—
x) on
[0,1]
are
Use
the DST and
ai,
02,
• •
•,
«es
to
estimate
/ on a
grid with
63
evenly spaced
points.
9.
Let /o,
/i,...,
/jv-i
be a
sequence
of
real numbers,
and
define
F
0
,
FI
,...,
FN-I
by
(9.15). Then
define
#
0
,£i,
•
• •
,9N-i
by
414
Chapter 9. More
about
Fourier series
6. Suppose u satisfies periodic boundary conditions on the interval [-£,
£],
and
<Xl
L cnei1fnx/l
n=-(XJ
is
the
complex Fourier series of u. Prove
that
is
the
complex Fourier series of -cPu/
dx
2
•
7.
Use the DST
to
estimate the first
15
Fourier coefficients of the function J(x) =
x(1 -
x)
on the interval
[0,1].
Compare
to
the exact values
4(-1
+
(-I)n)
an = - 3 3 ' n =
1,2,3,
....
n7r
8.
The
Fourier sine coefficients of J(x) =
x(l
-
x)
on
[0,1]
are
4(-1
+
(_l)n)
an = - 3 3 ' n =
1,2,3,
....
n7r
Use the DST and a1, a2,
...
,
a63
to
estimate J on a grid with 63 evenly spaced
points.
9.
Let
Jo,ft,
...
, IN-1
be
a sequence of real numbers, and define F
o
,F
1
,
...
, F
N
-
1
by (9.15).
Then
define 90,91,
...
,9N-1 by
N-1
(.)
9j
= 2 L
Fn
sin 7r;; , j = 0,1,
...
, N -
1.
n=l
Show
that
9j
=
2N
fJ,
j =
0,1,
...
, N -
1.
Hint: Proceed according
to
the
hint in Exercise
5.
You can use the fact
that
the
vectors
sin
(~)
I [ sin (
1V
)
sin
(2~"')
sin
(~)
.
((N~1)m1f)
, .
((;-1)j1f)
sm N sm N
are orthogonal in R
N
-
1
for
j,
m = 1,2,
...
, N
-1,
j
:j:.
m (see Exercise 3.5.7).
Also, each of these vectors has norm
IN/2
(see Exercise 9.1.7).
10.
The
DCT
maps a sequence {h}f=o of real numbers
to
the sequence
{Fn};;=o,
where
N-l
(.)
Fn=Jo+2~fJcos
7r;} +
(-l)nJN'
n=O,l,
...
,N.
3=1

9.3. Relationship
of
sine
and
cosine
series
to the
full Fourier
series
415
(a)
Reasoning
as in
Section 9.2.4, show
how the DCT can be
used
to
estimate
the
Fourier cosine
coefficients
of a
function
in
C[0,£j.
(b)
Reasoning
as in
Section 9.2.4, show
how the DCT can be
used
to
estimate
a
function
from
its
Fourier cosine
coefficients.
(c)
Modifying
the
technique presented
in
Section 9.2.5, show
how to
compute
the DCT
using
the DFT
(and hence
the
FFT). (Hint: Given
{fj}?
=0
,
define
{&*£„
by
and
treat
{fj}^-^
N
by the
three step process
on
page 405.)
(d)
Show
that
the DCT is its own
inverse,
up to a
constant
multiple.
To be
precise,
show
that
if the DCT is
applied
to a
given sequence
and
then
the
DCT
is
applied
to the
result,
one
obtains
IN
times
the
original sequence.
9.3
Relationship
of
sine
and
cosine
series
to the
full
Fourier
series
In
Section
9.1,
we
showed
that
the
complex
and
full
Fourier series
are
equivalent
for
a
real-valued
function.
We
will
now
show
that
both
the
Fourier cosine
and the
Fourier sine series
can be
recognized
as
special cases
of the
full
Fourier series
and
hence
of the
complex Fourier series.
This
will show
that
the
complex Fourier series
is
the
most general concept.
To
understand
the
relationships between
the
various Fourier series
for
real-
valued functions,
we
must understand
the
following
terms:
Definition
9.5.
Let f
:
R
->•
R.
Then
f is
1.
odd
if
f(-x)
=
—f(x)
for all x
G
R;
2.
even
if
f(—x)
—
j(x]
for all x 6 R;
3.
periodic with period
T
if
T >
0,
f(x
+ T) =
f(x]
for all x
e
R
;
and
this
condition
does
not
hold
for any
smaller positive value
ofT.
Examples
of odd
functions include polynomials with only
odd
powers
and
sin
(x).
Polynomials with only even powers
and cos (x) are
examples
of
even
func-
tions, while sine
and
cosine
are the
prototypical periodic functions (both have period
2?r).
The
algebraic properties
defining
odd and
even functions
imply
that
the
graph
of
an odd
function
is
symmetric through
the
origin, while
the
graph
of an
even
function
is
symmetric across
the
y-axis
(see Figure 9.5).
We
will
show
that
the
full
Fourier series
of an odd
function reduces
to a
sine
series,
and
that
the
full
Fourier series
of an
even function reduces
to a
cosine series.
We
need this preliminary result:
9.3. Relationship of sine and cosine series
to
the
full
Fourier series
415
(a) Reasoning as in Section 9.2.4, show how the
neT
can be used to estimate
the
Fourier cosine coefficients of a function in
C[O,
fl.
(b) Reasoning as in Section 9.2.4, show how the
neT
can be used
to
estimate
a function from its Fourier cosine coefficients.
(c)
Modifying the technique presented in Section 9.2.5, show how
to
compute
the
neT
using
the
nFT
(and hence
the
FFT).
(Hint: Given
{f;}.f=o,
-
N-l
define
{fj}
j=-N by
jj=fljl,
j=-N,-N+1,
...
,N-1,
and
treat
{jj}f=-l-N by the three step process on page 405.)
(d) Show
that
the
neT
is
its own inverse, up
to
a constant multiple.
To
be
precise, show
that
if the
neT
is
applied
to
a given sequence and then the
neT
is
applied
to
the result, one obtains
2N
times the original sequence.
9.3 Relationship
of
sine
and
cosine
series
to
the full
Fourier
series
In Section 9.1,
we
showed
that
the complex and full Fourier series are equivalent
for a real-valued function.
We
will now show
that
both
the Fourier cosine and
the
Fourier sine series can be recognized as special cases of the full Fourier series and
hence of the complex Fourier series. This will show
that
the complex Fourier series
is
the most general concept.
To
understand the relationships between the various Fourier series for real-
valued functions,
we
must understand the following terms:
Definition
9.5.
Let
f : R -+
R.
Then f is
1.
odd
if
f(
-x)
= -
f(x)
for all x E
R;
2.
even
if
f(
-x)
=
f(x)
for all x E
R;
3.
periodic with period T
if
T >
0,
f(x
+
T)
=
f(x)
for all x E
R,
and this
condition does
not
hold for any smaller positive value
of
T.
Examples of odd functions include polynomials with only odd powers
and
sin (x). Polynomials with only even powers and
cos
(x)
are examples of even func-
tions, while sine and cosine are the prototypical periodic functions (both have period
27f).
The algebraic properties defining odd and even functions imply
that
the graph
of
an
odd function
is
symmetric through the origin, while the graph of
an
even
function
is
symmetric across the y-axis (see Figure 9.5).
We
will show
that
the full Fourier series of an odd function reduces to a sine
series, and
that
the full Fourier series of an even function reduces
to
a cosine series.
We
need this preliminary result:
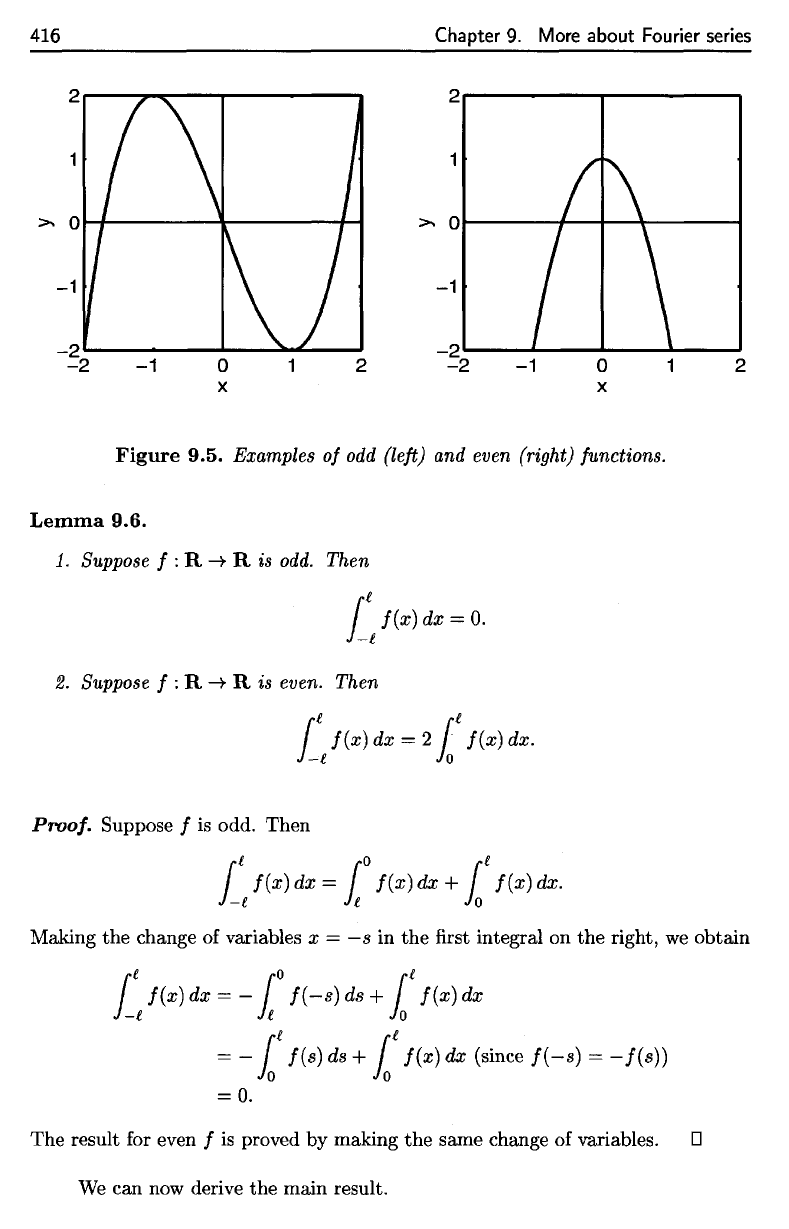
416
Chapter
9.
More about Fourier
series
Figure
9.5. Examples
of odd
(left)
and
even
(right)
functions.
Lemma 9.6.
1.
Suppose
f
:
R
—>•
R is
odd. Then
2.
Suppose
f
:
R
—>•
R is
even. Then
Proof. Suppose
/ is
odd. Then
Making
the
change
of
variables
x =
—
s in the first
integral
on the
right,
we
obtain
The
result
for
even
/ is
proved
by
making
the
same change
of
variables.
We
can now
derive
the
main result.
416
Chapter 9. More
about
Fourier series
2~---------r--------~
1
~
O~----~~-r--+-----~
-1
-2~--~----~----~--~
-1
o
x
1 2
-2
-1
o
x
Figure
9.5.
Examples of
odd
(left) and
even
(right) junctions.
Lemma
9.6.
1.
Suppose 1 : R
-+
R
is
odd.
Then
1ft
I(x)
dx =
o.
2.
Suppose 1 : R
-+
R is even. Then
(
I(x)
dx = 2
(f(x)
dx.
1-
t
10
Proof.
Suppose 1
is
odd. Then
rt
I(x)
dx = 1
0
f(x)
dx
+
r£
f(x)
dx.
1-
t
l
10
2
Making the change of variables x =
-s
in the first integral on the right,
we
obtain
rt
I(x)
dx =
-1
0
f(
-8)
ds
+
(f(x)
dx
1-£
£
10
=
-1£
I(s)
ds
+
1£
I(x)
dx (since
I(
-s)
= - I(s))
=
O.
The result for even 1
is
proved by making
the
same change of variables. D
We
can now derive
the
main result.

9.3.
Relationship
of
sine
and
cosine
series
to the
full Fourier
series
417
Theorem
9.7.
Let f 6
L
2
(—t,I),
and
suppose
that
is the
full
Fourier series
of
f.
1. If f is
odd. then
and
That
is, the
full
Fourier series
(on
[—1,
i])
of an odd
function
is the
same
as
its
Fourier sine series
(on
[0,f\).
2. If f is
even, then
6
n
= 0,
n
=
l,2,3,...
and
That
is,
the
full
Fourier series
(on
[—1,1])
of an
even function
is the
same
as
its
Fourier cosine series
(on
[Q,i]).
Proof.
If / is
odd, then
is
odd and
is
even. This,
together
with
the
previous lemma, yields
the first
result.
If
/ is
even, then
is
even
and
is
odd. Prom
this
we
obtain
the
second conclusion.
We
can use the
preceding result
in the
following fashion. Suppose
we
wish
to
understand
the
convergence
of the
Fourier sine series
of / : (0,
i)
—>•
R.
Define
fodd
'•
(—£•,£)
—>•
R-5
the odd
extension
of /, by
9.3. Relationship
of
sine
and
cosine
series
to
the full Fourier
series
Theorem
9.7.
Let f E
L2(-e,e),
and
suppose
that
is
the full Fourier series of
f·
1.
If
f
is
odd,
then
and
an =
0,
n =
0,1,2,
...
b
n
=
~
10£
f(x) sin
(n;x)
dx.
417
That
is,
the
full Fourier series (on [-e, f]) of
an
odd
function
is
the
same
as
its Fourier sine series
(on
[0,
el).
2.
If
f
is
even,
then
b
n
= 0, n =
1,2,3,
...
and
ao
=
~
10£
f(x)
dx,
2
r£
(n7rx)
an = C
10
f(x) cos
-f-
dx.
That
is,
the full Fourier series
(on
[-e,
e])
of
an
even function is the same
as
its Fourier cosine series
(on
[0,
fl).
Proof.
If
f
is
odd,
then
(
n7rx)
f(x)
cos -e-
is odd and
f(x)
sin
(n;x)
is
even. This, together with the previous lemma, yields
the
first result.
If
f
is
even, then
(
n7rx)
f(x)
cos -e-
is
even and
f(x)
sin
(n;x)
is odd. From this
we
obtain the second conclusion. 0
We
can use
the
preceding result in
the
following fashion. Suppose
we
wish
to
understand the convergence of the Fourier sine series of f : (0,
f)
-+
R.
Define
fodd
:
(-f,
f)
-+
R,
the
odd
extension of
f,
by
{
f(x),
o<x<e,
fOdd(X)
= _
f(
-x),
-e
< x <
0.
