Gockenbach M.S. Partial Differential Equations. Analytical and Numerical Methods
Подождите немного. Документ загружается.


448
Chapter
9.
More about Fourier
series
9.6.2
Mean-square
convergence
of
Fourier
series
Accepting
the
facts presented above about
L
2
(—£,£),
we can now
prove
the
desired
result.
Theorem
9.27.
// / €
L
2
(—l,t),
then
its
Fourier series
converges
to f in L
2
.
That
is,
let
be
the
complex
Fourier series
of
f,
and
define
Then
Proof.
We
must show
that
for any e > 0,
there exists
a
positive integer
7V
e
such
that
for
every
N
>
N
e
.
The
proof
is a
typical
e/3
argument—we
show
that
/N
is
close
to
/ by
using
the
triangle inequality with
two
intermediate
functions.
To be
specific,
let g be a
smooth
function
satisfying
g(—I)
=
g(i]
and
We
will
show
that
/N
is
close
to /
(for
TV
sufficiently
large)
by
showing
that
fw
is
close
to
QN
(where
QN
is the
corresponding partial Fourier series
for g) and
QN
is
close
to
g-
we
then
use the
fact
that
g is
close
to / by
construction.
Let
d
n
,n=:0,±l,±2,...be
the
Fourier
coefficients
of
p,
and
define
By
Corollary 9.23,
QN
—>•
g
uniformly
on
[—1,
£],
and
therefore
there
exists
a
positive
integer
N
f
such
that
It
follows
that
448
Chapter
9.
More about Fourier
series
9.6.2 Mean-square convergence
of
Fourier
series
Accepting
the
facts presented above about L2(
-£,
f),
we
can
now
prove
the
desired
result.
Theorem
9.27.
II I E L2(_£,£), then its Fourier series converges to I in
L2.
That is, let
n=-oo
be
the complex Fourier series
01
I,
and define
N
IN(X) = L
cneiomx/l.
n=-N
Then
III
-
INII£2
--+
0
as
N
--+
00.
Proof.
We
must show
that
for any € >
0,
there exists a positive integer N
f
such
that
III
-
INIIL2
< €
for every N
::::
N •. The proof
is
a typical €/3
argument-we
show
that
IN
is
close
to
I by using the triangle inequality with two intermediate functions.
To
be specific,
let
9 be a smooth function satisfying
g(
-f)
=
g(£)
and
€
III
-
gll£2
<
a'
We
will show
that
IN
is
close to I (for N sufficiently large) by showing
that
IN
is
close
to
gN
(where
gN
is
the corresponding partial Fourier series for
g)
and
gN
is
close to g;
we
then use
the
fact
that
9
is
close
to
I by construction.
Let
d
n
,
n = 0,
±1,
±2,
...
be
the
Fourier coefficients of g, and define
N
gN(X)
= L
dnei7rnx/l.
n=-N
By Corollary 9.23,
gN
--+
9 uniformly on [-£,
£],
and
therefore there exists a positive
integer N
f
such
that
It
follows
that

9.6. Mean-square convergence
of
Fourier
series
449
and so
Finally,
we
have
that
/AT
—
QN
is the
partial
Fourier series
of the
function
f
—
g,
and
hence
that
/AT
—
QN
is the
projection onto
the
space
spanned
by
It
follows
that
Thus
we
obtain
This completes
the
proof.
Now
that
we
have obtained this fundamental result,
we can
draw some
further
conclusions. First,
a
question
of
terminology:
the
above theorem shows
that
the
complex exponentials
e
™
nx
/
1
,
n
= 0, ±1,
±2,...,
are
complete
in
I/
2
(—£,£).
Definition
9.28.
Let V be an
(infinite-dimensional)
inner product
space.
We say
that
an
orthogonal
sequence
{<f>j}^i
is
complete
if
every
v £ V
satisfies
where
the
convergence
is in the
sense
of the
norm
on
V.
The
completeness
of an
orthogonal sequence
in an
infinite-dimensional inner
product space
is
thus analogous
to the
property
of
spanning
for a finite
collection
of
vectors
in a finite-dimensional
vector space. Moreover, orthogonality implies linear
independence,
so a
complete orthogonal sequence
for an
infinite-dimensional vector
space
is
analogous
to a
basis
for a finite-dimensional
vector space.
A
result
that
is
sometimes
useful
is the
following.
Theorem
9.29.
Let
{(f)j
:
j —
1,2,...}
be a
complete
orthogonal
sequence
in an
inner product
space
V.
Then
Proof.
By the
completeness
of
{</>j
: j =
1,2,...},
we
have,
for any v
e
V,
It
follows
immediately
that
if (v,
0j)y
= 0 for all j =
1,2,3,...,
then
v = 0.
9.6. Mean-square convergence
of
Fourier
series
449
and
so
f
IIg
-
gNII£2
< 3'
Finally,
we
have
that
iN
- gN is the partial Fourier series of
the
function i - g,
and
hence
that
iN
-
9N
is
the
projection onto
the
space spanned by
e
-i7rNx/l e-i7r(N-l)x/l ei7rNx/l
, , ...
,.
It
follows
that
Thus
we
obtain
This completes
the
proof. 0
Now
that
we
have obtained this fundamental result,
we
can draw some further
conclusions. First, a question of terminology:
the
above theorem shows
that
the
complex exponentials e
i7rnx
/£,
n =
0,
±1, ±2,
...
, are complete in L2( -C,
C).
Definition
9.28.
Let V
be
an (infinite-dimensional)
inner
product space. We say
that an orthogonal sequence
{t/>j
}i=l is complete
if
every v E V satisfies
where the convergence is
in
the sense
of
the
norm
on V.
The
completeness of
an
orthogonal sequence in
an
infinite-dimensional inner
product space is thus analogous
to
the
property of spanning for a finite collection of
vectors in a finite-dimensional vector space. Moreover, orthogonality implies linear
independence, so a complete orthogonal sequence for
an
infinite-dimensional vector
space is analogous
to
a basis for a finite-dimensional vector space.
A result
that
is sometimes useful is
the
following.
Theorem
9.29.
Let
{t/>j
: j = 1,2,
...
}
be
a complete orthogonal sequence
in
an
inner
product space
V.
Then
v E V, (v,t/>j)v = 0 for all j =
1,2,3,
...
~
v =
O.
Proof. By
the
completeness of
{t/>j
: j = 1,2,
...
},
we
have, for any v E
V,
v =
f:
(v,t/>j)v
t/>j.
j=l
(t/>j,
t/>j)v
(9.24)
It
follows immediately
that
if
(v,t/>j)v = 0 for all j =
1,2,3,
...
,
then
v =
O.
0

450
Chapter
9.
More
about Fourier
series
This result
justifies
a
fact
that
we
have used constantly
in
developing Fourier series
methods
for
BVPs:
Two
functions
are
equal
if and
only
if
they have
the
same
Fourier
coefficients.
Corollary
9.30.
Let
{fij
:
j =
1,2,...}
be a
complete
orthogonal
sequence
in an
inner product
space
V.
Then,
for any u, v
e
V,
Proof. Obviously,
if u = v,
then
(u,
0j)y
= (v,
0j)v
for all j. On the
other hand,
if
(u,
(f)j)v
=
(
v
>
0j)v
for all
j,
then
w = u
—
v
satisfies
By
the
preceding theorem, this implies
that
w = 0,
that
is,
that
u = v.
Finally, because
all
other Fourier series (sine, cosine,
full,
quarter-wave sine,
quarter-wave
cosine)
are
special cases
of the
complex Fourier series,
all of the
above
results extend
to
these other Fourier series
as
well.
For
example,
we
define
L
2
(0,^)
to be the
space
of all
measurable
functions
/ :
(0,^)
->
R
such
that
Then,
if /
e
£
2
(0,
£),
the
Fourier sine series
of /
converges
to / in the
mean-square
sense (see Exercise
6).
We
have
now
completed
the
basic theory used
in the
earlier chapters
of
this
book.
In the
next section,
we
discuss
one
further
point
for the
sake
of
tying
up a
loose
end.
9.6.3 Cauchy sequences
and
completeness
We
assume
that
{^j}^!
is an
orthogonal sequence
in an
inner product space
V
and
also, without loss
of
generality,
that
each
(f>j
has
norm
one (so the
sequence
is
orthonormal).
If v 6 V and
then,
by
Bessel's inequality,
We
now
consider
the
converse:
If
01,02,03,...
is any
sequence
of
complex
numbers
satisfying
450 Chapter 9. More
about
Fourier series
This result justifies a fact
that
we
have used constantly in developing Fourier series
methods for BVPs: Two functions are equal if and only if
they
have the same
Fourier coefficients.
Corollary
9.30.
Let
{¢j
: j =
1,2,
...
}
be
a complete orthogonal sequence
in
an
inner
product space
V.
Then,
for
any
u,
v E
V,
u = v
{:}
(u,
¢j)v
=
(v,¢j)v
for all j =
1,2,3,
....
Proof.
Obviously,
if
u =
v,
then
(u,
¢j)v
= (v,
¢j)v
for all
j.
On
the
other hand,
if
(u,
¢j)v
= (v,
¢j)v
for all
j,
then
w = u - v satisfies
(w,¢j)v
= ° for all j =
1,2,3,
....
By
the
preceding theorem, this implies
that
w = 0,
that
is,
that
u = v. 0
Finally, because all
other
Fourier series (sine, cosine, full, quarter-wave sine,
quarter-wave cosine) are special cases
of
the
complex Fourier series, all of the above
results extend
to
these
other
Fourier series as well. For example,
we
define
L2
(0,
£)
to
be
the
space of all measurable functions f : (0,
£)
-+
R such
that
Then, if f E L
2
(0, i),
the
Fourier sine series of f converges
to
f in
the
mean-square
sense (see Exercise 6).
We
have now completed
the
basic theory used in
the
earlier chapters of this
book. In
the
next section,
we
discuss one further point for the sake of tying up a
loose end.
9.6.3 Cauchy sequences and completeness
We assume
that
{¢j
}~l
is an orthogonal sequence in an inner product space V
and
also, without loss of generality,
that
each
¢j
has norm one (so
the
sequence is
orthonormal).
If
v E V and
(
,/,)
(v,¢j)v
aj=
v,'/'j
v=
(¢j,¢j)v'
j=1,2,3,
...
,
then, by Bessel's inequality,
DO
Llajl2
<
00.
j=l
We
now consider
the
converse:
If
al,
a2, a3,
.
..
is any sequence of complex
numbers satisfying
DO
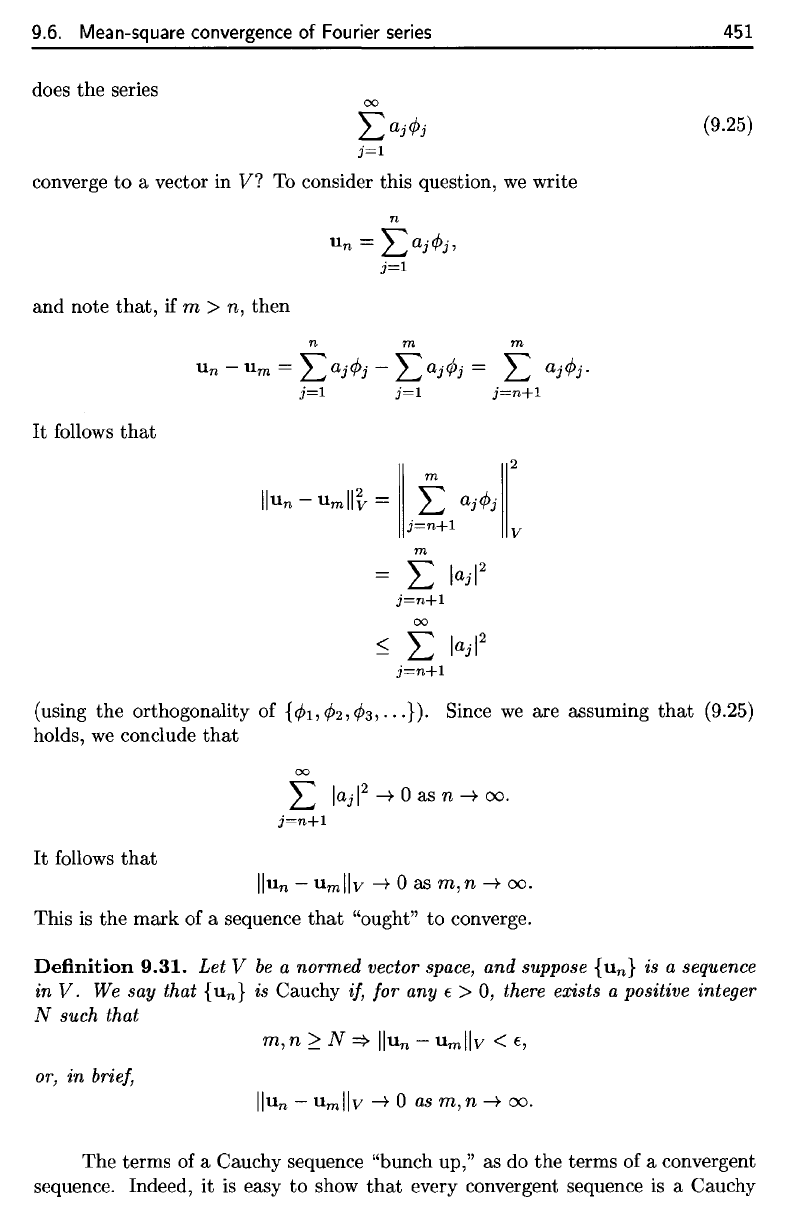
9.6. Mean-square convergence
of
Fourier
series
451
and
note
that,
if
m
>
n,
then
It
follows
that
or, in
brief,
The
terms
of a
Cauchy
sequence "bunch
up,"
as do the
terms
of a
convergent
sequence. Indeed,
it is
easy
to
show
that
every convergent sequence
is a
Cauchy
does
the
series
converge
to a
vector
in
VI
To
consider
this
question,
we
write
(using
the
orthogonality
of
{0i,
02,0s,
•••})•
Since
we are
assuming
that
(9.25)
holds,
we
conclude
that
It
follows
that
This
is the
mark
of a
sequence
that
"ought"
to
converge.
Definition
9.31.
Let V be a
normed
vector
space,
and
suppose
{u
n
}
is a
sequence
in
V.
We say
that
{u
n
}
is
Cauchy
if, for any e > 0,
there exists
a
positive integer
N
such that
9.6. Mean-square convergence
of
Fourier
series
does the series
00
Laj</>j
j=1
converge
to
a vector in V?
To
consider this question,
we
write
n
Un
= Laj</>j,
j=1
and note
that,
if m > n, then
n m m
Un
- U
m
=
L:aj</>j
-
Laj¢j
= L
aj</>j.
j=1
j=1
j=n+l
It
follows
that
2
m
IIU
n
-
umll~
= L
aj</>j
j=n+1
v
00
::;
L
lajl2
j=n+1
451
(9.25)
(using the orthogonality of
{¢1, ¢2, ¢3,
...
} ). Since
we
are assuming
that
(9.25)
holds,
we
conclude
that
It
follows
that
00
L
lajl2
-+
0 as n
-+
00.
j=n+1
Ilu
n
-
umllv
-+
0
as
m,n
-+
00.
This
is
the mark of a sequence
that
"ought" to converge.
Definition
9.31.
Let V
be
a normed vector space, and suppose {un} is a sequence
in
V.
We say that {un} is Cauchy if, for any f >
0,
there exists a positive integer
N such that
m,n
2:
N
=>
Ilu
n
-
umllv
<
f,
or,
in
brief,
Ilu
n
-
umllv
-+
0
as
m,n
-+
00.
The terms of a Cauchy sequence "bunch up," as do the terms of a convergent
sequence. Indeed, it
is
easy
to
show
that
every convergent sequence
is
a Cauchy

452
Chapter
9.
More
about
Fourier series
sequence.
On the
other hand,
the
converse (does every
Cauchy
sequence converge?)
depends
on the
space
as
well
as on the
norm
of the
space.
Example
9.32.
Define
a
sequence
of
rational numbers
{x
n
}
by the
rule that
x
n
is the
number
obtained
by
truncating
the
decimal expansion
of
IT
after
n
digits
(so
xi
= 3,
X2
=
3.1,
#3
=
3.14,
and so
on). Then
{x
n
}
is
certainly Cauchy
(ifm
> n,
then
\x
m
—x
n
\
<
W~
n+1
).
However,
the
question
of
whether
{x
n
}
converges
depends
on the
space
under consideration.
If
the
space
is Q, the set
of
rational numbers, then
{x
n
}
fails
to
converge.
On the
other hand,
if
the
space
is R,
then
{x
n
}
converges,
and the
limit
is the
irrational number
TT.
This
last
example
may
seem
rather
trivial;
it
just
points
out the
fact
that
the
real
number system contains numbers
that
are not
rational,
and
that
without
the
irrational
numbers there
are
"holes"
in the
system.
The
next example
is
more
relevant
to our
study.
Example
9.33.
Define
f
:
[0,1]
-»•
R by
Let
/AT
:
[0,1]
—>•
R be the
function
defined
by the
partial Fourier sine series
of
f
with
N
terms. Then
\\f —
/N\\L*
~*
0
as
n
—>
°°j
so
{fn}
is
convergent
and
hence
Cauchy. However,
if the
space
under consideration
is
(7[0,1],
the
space
of all
continuous functions
defined
on the
interval
[0,1],
and the
norm
is the L
2
norm,
then
{/AT}
is
still Cauchy
and yet is not
convergent
(since
f
0
C[0,1]).
We
see
that
the
second example
is
analogous
to the first. The
space
(7[0,1],
which
is a
subspace
of
L
2
(0,1),
has
some "holes"
in it, at
least when
the
norm
is
taken
to be the
L
2
norm.
We
have
a
name
for a
space
in
which every Cauchy sequence converges.
Definition
9.34.
Let V be a
normed vector
space.
If
every
Cauchy sequence
in V
converges
to an
element
of
V,
then
we say
that
V is
complete.
We
now
have
two
different
(and
unrelated)
uses
for the
word
"complete."
An
orthogonal sequence
in an
inner product space
can be
complete,
and a
normed
vector space
can be
complete.
The
above examples show
that
Q is not
complete,
and
neither
is
C[0,1]
under
the
L
2
norm.
73
On the
other hand,
R is
complete
(as is
R
n
).
Also,
the
space
L
2
(0,1)
is
complete,
the
proof
of
which result
is
beyond
the
scope
of
this book.
73
A
standard result
from
analysis
is
that
C[0,1]
is
complete under
a
different
norm, namely,
the
norm
of
uniform
convergence:
This result
follows
from
the
fact
that
if a
sequence
of
continuous functions converges
uniformly
to
a
function,
the
limit
function
must also
be
continuous.
452 Chapter 9. More
about
Fourier series
sequence. On the other hand,
the
converse (does every Cauchy sequence converge?)
depends on the space as
well
as on the norm of the space.
Example
9.32.
Define a sequence
of
rational numbers
{xn}
by
the rule that
Xn
is the number obtained
by
truncating the decimal expansion
of
11"
after n digits
{so
Xl
= 3,
X2
= 3.1,
X3
= 3.14, and so on}. Then
{xn}
is certainly Cauchy
{ifm
>
n,
then
/x
m
-x
n
/ < lO-n+1}. However, the question
of
whether
{xn}
converges depends
on the space under consideration.
If
the space is Q, the set
of
rational numbers, then
{xn}
fails to converge. On the other hand,
if
the space
is
R,
then
{xn}
converges,
and the limit is the irrational number
11".
This last example may seem rather trivial;
it
just points
out
the
fact
that
the real number system contains numbers
that
are not rational, and
that
without
the irrational numbers there are "holes" in
the
system. The next example is more
relevant
to
our study.
Example
9.33.
Define f :
[0,
1]
-+
R by
f(x)
=
{I,
X E
[~,~)
,
0,
XE[2,1].
Let
fN
:
[0,1]
-+
R
be
the function defined
by
the partial Fourier sine series
of
f with N terms. Then IIf -
fNIIL2
-+
°
as
n
-+
00,
so
{In}
is convergent and
hence Cauchy. However,
if
the space under consideration is e[O,I], the space
of
all
continuous functions defined on the interval
[0,1],
and the
norm
is the
L2
norm,
then
{IN}
is still Cauchy and yet is
not
convergent (since f ¢
C[O,
1]).
We
see
that
the second example is analogous
to
the first. The space
e[o,
1],
which
is
a subspace of L2(0, 1), has some "holes" in it,
at
least when
the
norm
is
taken
to
be
the
L2
norm.
We
have a name for a space in which every Cauchy sequence converges.
Definition
9.34.
Let V
be
a normed vector space.
If
every Cauchy sequence
in
V
converges to an element
of
V,
then
we
say that V is complete.
We
now have two different (and unrelated) uses for the word "complete." An
orthogonal sequence in an inner product space can be complete, and a normed
vector space can be complete.
The above examples show
that
Q
is
not complete, and neither
is
e[O,
1]
under
the
L2
norm.
73
On the other hand, R
is
complete (as is Rn). Also, the space
L2(0,1)
is
complete,
the
proof of which result
is
beyond
the
scope of this book.
73
A
standard
result from analysis is
that
e[O,I] is complete under a different norm, namely,
the
norm
of uniform convergence:
11/1100
= max {If(x)1 : x E
[0,
In.
This
result follows from
the
fact
that
if a sequence of continuous functions converges uniformly
to
a function,
the
limit function
must
also
be
continuous.

9.6. Mean-square convergence
of
Fourier
series
453
Theorem
9.35. Both
real
and
complex
L
2
(a,b)
are
complete
spaces.
We
can now
answer
the
question
we
posed
at the
beginning
of
this section:
If
{0j}
is an
orthonormal sequence
in a
complex inner product space
V and
{a,j}
is a
sequence
of
complex numbers satisfying
converges
to an
element
ofV.
Proof. Since
V is
complete,
it
suffices
to
show
that
the
sequence
{v
n
}
of
partial
sums,
is
Cauchy.
If
m
>
n,
then
and, since
the
sequence
{4>j}
is
orthonormal,
we
have
Since
the
series
does
converge
to an
element
of
VI
The
answer
is
that
if V is
complete,
the
convergence
is
guaranteed.
Theorem
9.36.
Let V be a
complete
(complex)
inner product
space,
and let
<^i>02,03,
• • • be an
orthonormal sequence
in
V.
If
01,02,03,...
is a
sequence
of
complex
numbers
satisfying
then
9.6. Mean-square convergence
of
Fourier
series
453
Theorem
9.35.
Both real and complex L2(a,
b)
are
complete spaces.
We
can now answer
the
question
we
posed
at
the beginning of this section: If
{
<pj}
is
an orthonormal sequence in a complex inner product space V and {aj}
is
a
sequence of complex numbers satisfying
00
Llajl2
<
00,
j=1
does
00
L
aj<pj
j=1
converge
to
an element of V? The answer
is
that
if V
is
complete, the convergence
is
guaranteed.
Theorem
9.36.
Let V
be
a complete (complex) inner product space, and let
<PI,
<P2, <P3,
.
..
be
an orthonormal sequence
in
V.
If
aI,
a2, a3,
...
is a sequence
of
complex numbers satisfying
00
then
converges to an element
of
V.
Proof.
Since V
is
complete, it suffices
to
show
that
the sequence
{v
n}
of partial
sums,
is
Cauchy.
If
m >
n,
then
n
Vn
= L
aj<pj,
n =
1,2,3,
...
,
j=1
m
Vm
-
Vn
= L
aj<pj,
j=n+l
and, since the sequence
{<pj}
is
orthonormal,
we
have
m
00
j=n+l j=n+l
Since
the
series
00

(a)
Explain
why
this series converges
to a
function
/ 6
L
2
(0,1).
(b)
Graph
the
partial
sine series with
TV
terms,
for
various values
of
TV,
and
guess
the
function
/.
Then
verify
your guess
by
calculating
the
Fourier
sine
coefficients
of /.
where
c
n
=
1/n
for
n
^
0, and
CQ
— 0.
(a)
Explain
why
this series converges
to a
function
/ in
(complex)
£
2
(-l,
1).
(b)
Graph
the
partial
series with
2TV
+ 1
terms,
for
various values
of
TV,
and
guess
the
function
/.
Then
verify
your guess
by
calculating
the
Fourier
coefficients
of /.
3.
Does
the
sine series
converge
in the
mean-square sense
to a
function
/ €
£
2
(0,1)?
Why or why
not?
454
Chapter
9.
More about Fourier
series
is
convergent,
its
tail must converge
to
zero, which shows
that
This completes
the
proof.
The
conclusion
of all
this
is
that
if a
(complex) inner product space contains
a
complete orthonormal sequence
{0j},
then there
is a
one-to-one correspondence
between
V and the
space
The
vector
v 6 V
corresponds
to
{(v,
(f>j)v}
G
^
2
-
In
certain regards, then,
V and
I
2
are
really
the
same space, with
the
elements given
different
names.
We say
that
V and
I
2
are
isomorphic.
In
particular,
L
2
(—l,l)
and
I
2
are
isomorphic,
and
I/
2
(0,^)
is
isomorphic
to
real
£2.
Exercises
1.
Consider
the
sine series
2.
Consider
the
series
454
Chapter 9. More
about
Fourier series
is
convergent, its tail must converge to zero, which shows
that
Ilv
m
-
vnllv
-t
°
as
n,m
-t
00.
This completes
the
proof. 0
The conclusion of all this
is
that
if a (complex) inner product space contains
a complete orthonormal sequence
{cPj},
then there
is
a one-to-one correspondence
between
V
and
the space
The vector v
E V corresponds to {(v,
cPj)v}
E
f2.
In certain regards, then, V and
f2
are really
the
same space, with
the
elements given different names.
We
say
that
V
and
£2
are isomorphic.
In particular, L2(
-£,
£)
and
£2
are isomorphic, and L2(0,
£)
is
isomorphic
to
real
£2.
Exercises
1.
Consider the sine series
00
1
2:
;;:
sin (mfx).
n=l
(a) Explain why this series converges
to
a function f E L2(0,
1).
(b)
Graph the partial sine series with N terms, for various values of
N,
and
guess the function
f.
Then verify your guess by calculating the Fourier
sine coefficients of
f.
2.
Consider
the
series
00
L
cnein7rx,
n=-oo
where C
n
=
lin
for n
i'
0, and
Co
=
0.
(a) Explain why this series converges
to
a function f in (complex) L2(
-1,1).
(b) Graph the partial series with
2N
+ 1 terms, for various values of
N,
and
guess the function f. Then verify your guess by calculating
the
Fourier
coefficients of
f.
3. Does the sine series
00
1
~
vn
sin (mfx)
converge in the mean-square sense
to
a function f E L2(0,
I)?
Why or why
not?

9.7.
A
note about
general
eigenvalue
problems
455
4.
Consider
the
function
/ :
[0,1]
—»•
R
defined
by
/(#)
=
x
1
/
4
(l
—
x), and its
Fourier sine series
(a)
Which
of the
convergence theorems
of
this
chapter
apply
to /?
What
kind
of
convergence
is
guaranteed: pointwise,
uniform,
mean-square?
(b)
Estimate
01,02,...
,
OBS
using some
form
of
numerical integration. (One
option
is to use the
DST,
as
described
in
Section 9.2.4. Another possi-
bility
is to use the
formula
and
some
form
of
numerical integration.
In
this case, because
of the
singularity
at x — 0, it is a
good idea
to
change variables
so
that
the
integrand
is
smooth.
Use x —
s
4
.)
(c)
Graph
/
together
with
its
partial
Fourier sine series. Also graph
the
difference
between
the two
functions.
5.
(a) For
what values
of k
does
the
function
/ :
[0,1]
-»
R
defined
by
f(x)
=
x
k
belong
to
L
2
(0,1)?
(Consider
both
positive
and
negative values
of k.)
(b)
Estimate
the first 63
Fourier sine
coefficients
of
f(x)
=
x"
1
/
4
.
(c)
Graph
/(#)
=
x
-1
/
4
,
together with
its
partial
Fourier sine series (with
63
terms). Also graph
the
difference
between
the two
functions.
6.
Prove
that
if / 6
L
2
(Q,€),
then
the
Fourier sine series
of /
converges
to / in
the
mean-square sense.
7.
Let
{vj}
be a
sequence
of
vectors
in a
normed vector space
V, and
suppose
Vj
->
v E
V.
Prove
that
{vj}
is
Cauchy.
9.7 A
note about general eigenvalue problems
We
will
now
briefly
discuss
the
general eigenvalue problem
We
assume
that
fJ
is a
bounded domain
in
R
2
with
a
smooth boundary,
and
that
the
coefficient
k is a
smooth
function
of x
satisfying
fc(x)
>
ko
> 0 for all x €
f).
We
have already seen,
for a
constant
coefficient
and the
case
in
which
£)
is
a
rectangular domain
or a
disk,
that
(9.26)
has an
infinite sequence
of
solutions.
Moreover,
the
eigenpairs
had
certain properties
that
we
could
verify
directly:
the
eigenvalues were positive,
the
eigenfunctions were orthogonal,
and so
forth.
The
properties
we
observed
in
Sections
8.2 and 8.3
extend
to the
general
eigenvalue problem
(9.26),
although they cannot
be
verified
by
directly computing
9.7. A note about general eigenvalue problems
455
4.
Consider the function f : [0,1]
-t
R defined by
f(x)
= X
1
/
4
(1
- x), and its
Fourier sine series
00
L an sin (mrx).
n=l
(a) Which of
the
convergence theorems of this chapter apply
to
f?
What
kind of convergence
is
guaranteed: pointwise, uniform, mean-square?
(b) Estimate
aI,
a2,
...
,a63 using some form of numerical integration. (One
option is to use the DST, as described in Section
9.2.4. Another possi-
bility
is
to use the formula
an =
210
1
Xl/4(1_
x)
sin (mrx)
dx
and some form of numerical integration. In this case, because of the
singularity
at
x = 0, it
is
a good idea to change variables
so
that
the
integrand
is
smooth. Use x = 8
4
.)
(c)
Graph f together with its partial Fourier sine series. Also graph the
difference between
the
two functions.
5.
(a) For what values of k does the function f :
[0,
1]-t
R defined by
f(x)
= xk
belong
to
L2(0, 1)? (Consider both positive and negative values of
k.)
(b) Estimate the first
63
Fourier sine coefficients of
f(x)
= X-
1
/
4
.
(c)
Graph
f(x)
=
x-
1
/
4
,
together with its partial Fourier sine series (with
63
terms). Also graph the difference between the two functions.
6.
Prove
that
if f E L2(0, f), then the Fourier sine series of f converges to f in
the mean-square sense.
7.
Let
{Vj}
be a sequence of vectors in a normed vector space V, and suppose
Vj
-t
v E V. Prove
that
{Vj}
is
Cauchy.
9.7
A note about general eigenvalue problems
We
will now briefly discuss
the
general eigenvalue problem
-\7.
(k(x)\7u) =
AU
in
n,
u = ° on
an.
(9.26)
We
assume
that
n
is
a bounded domain in R2 with a smooth boundary, and
that
the coefficient k
is
a smooth function of x satisfying k(x)
:2:
ko
> ° for all x E
n.
We
have already seen, for a constant coefficient and the case in which n
is
a rectangular domain or a disk,
that
(9.26) has an infinite sequence of solutions.
Moreover, the eigenpairs had certain properties
that
we
could verify directly: the
eigenvalues were positive, the eigenfunctions were orthogonal, and so forth.
The properties
we
observed in Sections 8.2 and 8.3 extend
to
the
general
eigenvalue problem (9.26), although they cannot be verified by directly computing

456
Chapter
9.
More about Fourier
series
the
eigenpairs. Instead,
the
results
can be
deduced
from
some
fairly
sophisticated
mathematical arguments
that
are
beyond
the
scope
of
this book. Therefore,
we
will
not
attempt
to
justify
all of our
statements
in
this section.
We
define
Kr>
:
C&(ti)
by
so
that
(9.26)
can be
written
as
simply
The
following
results hold:
1. All
eigenvalues
of KD are
real
and
positive.
To
show this,
we
assume
that
KDU
=
\u
and
(u,u)
=
I.
Then
(The reader should notice
that,
since
we
cannot assume
a
priori
that
A and
u are
real,
we use the
complex
I/
2
inner product.)
This
shows
that
A is a
nonnegative real number. Moreover,
the
last
step
following
from
the
Dirichlet boundary conditions. Therefore,
KD
has
only positive eigenvalues.
2.
Eigenfunctions
of KD
corresponding
to
distinct eigenvalues
are
orthogonal.
As
we
have seen
before,
the
orthogonality
of
eigenfunctions depends only
on
the
symmetry
of the
operator, which
is
easy
to
verify
using integration
by
parts
(see Exercise
1).
3. The
operator
KD has an
infinite
sequence
{\
n
}^L
1
of
eigenvalues satisfying
456
Chapter
9.
More about Fourier
series
the
eigenpairs. Instead, the results can be deduced from some fairly sophisticated
mathematical arguments
that
are beyond the scope of this book. Therefore,
we
will
not
attempt
to
justify all of our statements in this section.
We
define
KD
:
e1(n)
by
KDu
=
-\7.
(k(x)\7u) ,
so
that
(9.26) can be written as simply
KDU =
AU.
The
following results hold:
1.
All eigenvalues of
KD
are real and positive. To show this,
we
assume
that
KDU =
AU
and (u,u) =
1.
Then
A =
A(U,U)
=
(AU,U)
= (KDu,u) = L (KDU)U
= - L
\7
. (k(x)\7u) U
= r k(x)\7u. \7u - r
k(x)u~U
Jn
Jan
un
= L k(x)\7u . \7u
= L k(x)
II\7u112
.
(The reader should notice
that,
since
we
cannot assume a priori
that
A and
U are real,
we
use the complex
L2
inner product.) This shows
that
A
is
a
nonnegative real number. Moreover,
A = 0 =? L k(x)
II\7u112
= 0
=? \7u = 0 (since k(x) >
0)
=?
u(x) = constant
=?
u(x) = 0,
the last step following from the Dirichlet boundary conditions. Therefore,
KD
has only positive eigenvalues.
2.
Eigenfunctions of
KD
corresponding
to
distinct eigenvalues are orthogonal.
As
we
have seen before, the orthogonality of eigenfunctions depends only on
the symmetry of the operator, which
is
easy
to
verify using integration by
parts
(see Exercise 1).
3.
The
operator
KD
has
an
infinite sequence
{An}~=l
of eigenvalues satisfying

74
The
technique
for
doing this
is
called
the
Gram-Schmidt procedure;
it is
explained
in
elemen-
tary linear algebra texts such
as
[34].
9.7.
A
note about general eigenvalue problems
457
and
In the
sequence
{A
n
},
each eigenvalue
is
repeated according
to the
dimension
of
the
associated eigenspace,
that
is,
according
to the
number
of
linearly
in-
dependent eigenfunctions associated with
that
eigenvalue.
In
particular, each
eigenvalue corresponds
to
only
finitely
many linearly independent eigenfunc-
tions.
It is
always possible
to
replace
a
basis
for a finite-dimensional
subspace
by an
orthogonal
basis.
74
Therefore,
all of the
eigenfunctions
of
KD
can be
taken
to be
orthogonal.
We
will
assume
that
{^n}^Li
is an
orthogonal sequence
satisfying
4. The set of
eigenfunctions
{ip
n
}
is a
complete orthogonal sequence
in
Z/
2
(fi):
For
each
/ 6
L
2
(ft),
the
series
converges
in the
mean-square sense
to /. The
space
L
2
(J7)
is
defined
as
was L
2
(a,
&)—informally,
it is the
space
of
square-integrable functions
defined
on
il,
with
the
understanding
that
if two
functions
differ
only
on a set of
measure zero, then they
are
regarded
as the
same.
The
series
(9.27)
is
called
a
generalized Fourier series
for /.
For
specific
domains,
it may be
more convenient
to
enumerate
the
eigenvalues
and
eigenfunctions
in a
doubly indexed list rather
than
a
singly indexed list
as
suggested
above.
For
example,
the
eigenvalue/eigenfunction pairs
of the
negative Laplacian
on
the
unit square
are
It is
possible (although
not
necessarily
useful)
to
order
the
\
mn
and
^
mn
in
(singly-
indexed)
sequences.
The
usefulness
of the
above facts
for
many computational tasks
is
limited,
since,
for
most domains
f)
and
coefficients
fc(x), it is not
possible
to
obtain
the
eigenvalues
and
eigenfunctions analytically
(that
is, in
"closed
form").
However,
as
we
have seen before,
the
eigenpairs give some information
that
can be
useful
in its
own
right.
It may be
useful
to
expend some
effort
in
computing
a few
eigenpairs
numerically.
We
illustrate this with
an
example.
Example
9.37. Consider
a
membrane that
at
rest
occupies
the
domain
tl,
and
suppose
that
the
(unforced)
small transverse vibrations
of the
membrane
satisfy
the
9.7. A note
about
general eigenvalue problems
457
and
An
-+
00
as n
-+
00.
In
the
sequence {An}, each eigenvalue
is
repeated according
to
the dimension
of the associated eigenspace,
that
is, according to
the
number of linearly in-
dependent eigenfunctions associated with
that
eigenvalue. In particular, each
eigenvalue corresponds to only finitely many linearly independent eigenfunc-
tions.
It
is
always possible to replace a basis for a finite-dimensional subspace by an
orthogonal basis.
74
Therefore, all of
the
eigenfunctions of
KD
can be taken
to be orthogonal.
We
will assume
that
{~n}~=l
is
an orthogonal sequence
satisfying
4.
The set of eigenfunctions
{~n}
is
a complete orthogonal sequence in L2(0):
For each f E L2(0), the series
(9.27)
converges in the mean-square sense to
f. The space L2(0)
is
defined as
was
L2(a, b)-informally, it
is
the space of square-integrable functions defined
on
0,
with the understanding
that
if two functions differ only on a set of
measure zero, then they are regarded as the same. The series (9.27)
is
called
a
generalized Fourier series for f.
For specific domains, it may be more convenient to enumerate the eigenvalues and
eigenfunctions in a doubly indexed list rather
than
a singly indexed list as suggested
above. For example, the eigenvalue/eigenfunction pairs of the negative Laplacian
on the unit square are
It
is
possible (although not necessarily useful) to order
the
Amn
and
~mn
in (singly-
indexed) sequences.
The usefulness of the above facts for many computational tasks
is
limited,
since, for most domains 0
and
coefficients k(x), it
is
not possible
to
obtain
the
eigenvalues and eigenfunctions analytically
(that
is, in "closed form"). However, as
we
have seen before, the eigenpairs give some information
that
can be useful in its
own right.
It
may be useful
to
expend some effort in computing a
few
eigenpairs
numerically.
We
illustrate this with an example.
Example
9.37.
Consider a membrane that at rest occupies the domain
0,
and
suppose that the (unforced) small transverse vibrations
of
the membrane satisfy the
74The technique for doing
this
is called
the
Gram-Schmidt
procedure;
it
is explained
in
elemen-
tary
linear algebra
texts
such as
[34].
