Giga Y. Surface Evolution Equations: A Level Set Approach
Подождите немного. Документ загружается.

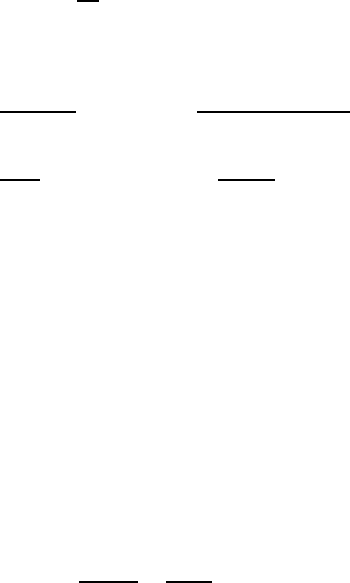
28 Chapter 1. Surface evolution equations
corresponding to the decomposition of the tangent space R
N
= T
x
0
R
N
of form
R
N
= T
x
0
Γ ⊕ N
x
0
Γ,
where N
x
0
Γ denotes the normal vector space at x
0
. Thus the eigenvalues of
˜
A
x
0
consist of principal curvatures κ
1
,...,κ
N−1
and 0.
We shall derive the level set representation of various curvatures from (1.4.5).
The mean curvature H at x
0
∈ Γ in the direction of n(x
0
) (defined by (1.4.1)) is
H = κ
1
+ ···+ κ
N−1
+0=trace
˜
A
x
0
=
1
|p|
traceQ
p
(X)withp = ∇u(x
0
),X= ∇
2
u(x
0
)
Since R
2
p
= R
p
by (1.4.3) and trace (R
p
XR
p
) = trace(R
2
p
X), H is of the form
H =
1
|∇u(x
0
)|
trace
I −
∇u(x
0
) ⊗∇u(x
0
)
|∇u(x
0
)|
2
∇
2
u(x
0
)
=
1
|∇u|
⎛
⎝
⎛
⎝
∆u −
1≤1,j≤N
u
x
i
u
x
j
|∇u|
2
⎞
⎠
u
x
i
x
j
⎞
⎠
at x = x
0
, (1.4.6)
where u
x
i
= ∂u/∂x
i
, u
x
i
x
j
= ∂
2
u/∂x
i
∂x
j
and ∆u =
N
j=1
u
x
j
x
j
.Form-th sym-
metric curvature with m ≤ N − 1bytheformof
˜
A
x
we see
H
m
= e
m
(κ
1
,...,κ
N−1
, 0)
where κ
1
,...,κ
N−1
, 0 are eigenvalues of Q
p
(X)/|p| with p=∇u(x
0
), X =∇
2
u(x
0
),
since
e
m
(κ
1
,...,κ
N−1
, 0) = e
m
(κ
1
,...,κ
N−1
).
If m = N − 1, then the Gaussian curvature K is of the form
K = e
N−1
(κ
1
,...,κ
N−1
, 0) = e
N−1
(κ
1
,...,κ
N−1
)=e
N
(κ
1
,...,κ
N−1
, 1).
This observation gives a simple representation of the Gaussian curvature
K =det
Q
p
(X)
|p|
+
p ⊗ p
|p|
2
,p= ∇u(x
0
),X= ∇
2
u(x
0
)(1.4.7)
since the eigenvalues of Q
p
(X)/|p| + p ⊗ p/|p|
2
are κ
1
,...,κ
N−1
, 1. If we arrange
κ
1
≤···≤ κ
N−1
, κ
i
(1 ≤ i ≤ N − 1) is written as
κ
i
= k
i
(p, X),p= ∇u(x
0
) =0,X= ∇
2
u(x
0
)
where k
i
(p, X) ≤ k
2
(p, X) ≤ ··· ≤ k
N−1
(p, X) are the eigenvalues of the linear
operator Q
p
(X)/|p| the orthogonal complement of the vector p. By this expression
it is possible to express the m-th symmetric curvature by u.
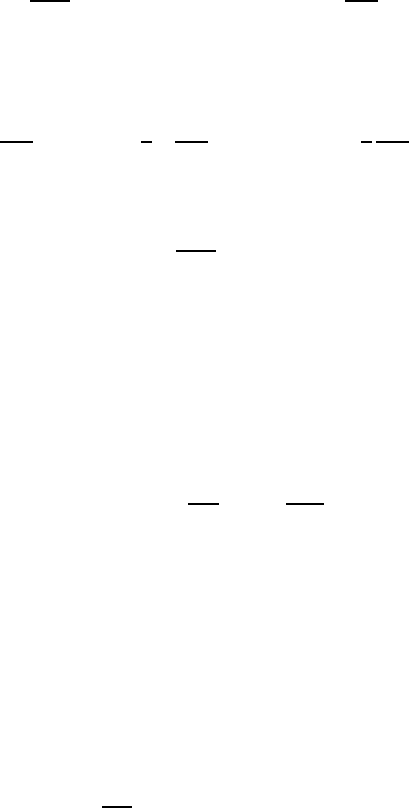
1.4. Expression of curvature tensors 29
There is another way to derive the level set representation of the mean cur-
vature and anisotropic mean curvature without using the representation (1.4.5)
but using surface divergence. We set m = −∇u/|∇u| and note that the vector
field m is defined not only on Γ but also on some neighborhood of Γ near x
0
.Itis
an extension of n in a neighborhood of Γ. By (1.3.6) we observe that
H = −div
Γ
n = −trace((I − n(x
0
) ⊗ n(x
0
))(∇m)(x
0
))
= −trace(∇m(x
0
)) + trace(n(x
0
) ⊗ n(x
0
)(∇m)(x
0
))
=div
∇u
|∇u|
(x
0
)+
1≤i, j≤N
n
i
(x
0
)n
j
(x
0
)(
∂
∂x
j
m
i
)(x
0
), (1.4.8)
where n =(n
1
,...,n
N
), m =(m
1
,...,m
N
). Here div denotes the divergence of a
vector field on R
N
.Sincem is a unit vector field near x
0
,
N
i=1
n
i
(x
0
)
∂
∂x
j
m
i
(x
0
)=
1
2
∂
∂x
j
N
i=1
m
2
i
(x
0
)=
1
2
∂
∂x
j
1=0.
Thus the last term of (1.4.8) disappears and we obtain
H =
div
∇u
|∇u|
(x
0
)(1.4.9)
which is the same as (1.4.6).
We shall give a level set representation of anisotropic mean curvature. We
recall (1.3.6) to calculate
h = −div
Γ
ξ(n)=−trace{(I − n(x
0
) ⊗ n(x
0
))(∇ξ(m))(x
0
)}
= −trace(∇ξ(m))(x
0
)+trace{(n(x
0
) ⊗ n(x
0
))(∇ξ(m))(x
0
)}. (1.4.10)
The second term is of form
1≤i,k,≤N
n
i
(x
0
)n
j
(x
0
)
∂ξ
i
∂p
(n(x
0
))
∂m
∂x
j
(x
0
)
with ξ =(ξ
1
,...,ξ
N
). Since ξ = ∇γ and γ is positively homogeneous of degree 1
so that
γ(λp)=λγ(p),λ>0,
differentiating in p
yields
λξ
(λp)=λξ
(p)orξ
(λp)=ξ
(p)for1≤ ≤ N.
In other words ξ
is positively homogeneous of degree zero. Differentiating in λ
and setting λ = 1 yields the Euler equation
N
i=1
p
i
∂ξ
∂p
i
(p)=0, 1 ≤ ≤ N. (1.4.11)
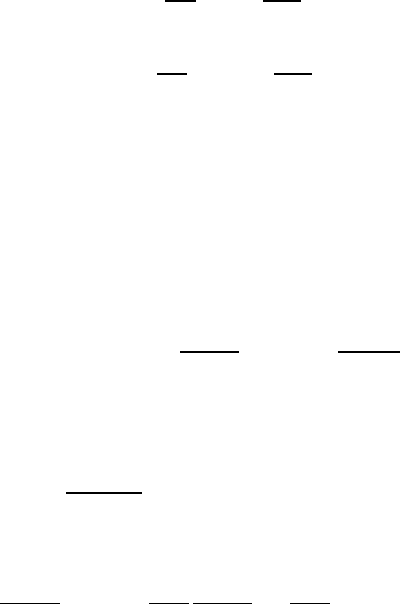
30 Chapter 1. Surface evolution equations
Since ∂ξ
/∂p
i
= ∂ξ
i
/∂p
, the second term of (1.4.10) can be rewritten as
1≤i,j,≤N
n
i
(x
0
)n
j
(x
0
)
∂ξ
∂p
i
(n(x
0
))
∂m
∂x
j
(x
0
)
=
1≤i,j,≤N
N
i=1
n
i
(x
0
)
∂ξ
∂p
i
(n(x
0
))
∂m
∂x
j
(x
0
)n
j
(x
0
)=0 by(1.4.11).
Thus we have
h = −(div ξ(m))(x
0
); (1.4.12)
note that this formula holds for any extension m of n in a tubular neighborhood of
Γnearx
0
since we do not use the property |m| =1.Instead,ξ should be a Cahn–
Hoffman vector. If γ(p)=|p| so that ξ = p/|p|, we recover the formula (1.4.9) with
m = −∇u/|∇u|.Sinceξ is homogeneous of degree zero, (1.4.12) yields
h = −div(ξ(−∇u))(x
0
)
=
1≤i,j≤N
∂
2
γ
∂p
i
∂p
j
(−∇u(x
0
))
∂
2
u
∂x
i
∂x
j
(x
0
). (1.4.13)
(Of course if γ(p)=|p|, this again yields (1.4.9).) By (1.4.11) we see R
p
∇
2
γ(p)=
∇
2
γ(p)=∇
2
γ(p)R
p
. From (1.4.13) it now follows that
h =
1
|∇u(x
0
)|
trace
∇
2
γ(n(x
0
))Q
n(x
0
)
(∇
2
u)(x
0
)
(1.4.14)
with n(x
0
)=−∇u(x
0
)/|∇u(x
0
)| since ∂
2
γ/∂p
i
∂p
j
is homogeneous of degree −1
so that
∂
2
γ
∂p
i
∂p
j
(−∇u)=
1
|∇u|
∂
2
γ
∂p
i
∂p
j
−
∇u
|∇u|
, 1 ≤ i, j ≤ N.
Using the second fundamental form in (1.4.14) we have
h =trace(∇
2
γ(n(x
0
))
˜
A
x
0
). (1.4.15)
The formula (1.4.15) may explain a reason why h is sometimes called a weighted
mean curvature.
Graph representation. It is easy to derive a formula for the second fundamen-
tal form from (1.4.5) when Γ is given as the graph of a function. By rotating
coordinates we may assume that Γ is expressed as
Γ={x
N
= g(x
),x
∈ R
N−1
}
around x
0
∈ Γ, where g(x
0
)=x
0N
.Ifn is taken upward, then Γ is given as the
zero level set of
u(x)=−x
N
+ g(x
)

1.4. Expression of curvature tensors 31
with n = −∇u/|∇u| which is the same as (1.1.2). Plugging in (1.4.5) we obtain a
formula of
˜
A
x
0
written by g. A general formula is complicated so we do not give it
here. However if ∇
g(x
0
)=0sothatn(x
0
)=(0, 0,...,0, 1), then the expression
of
˜
A
x
0
is simple. Indeed, since ∇u(x
0
)=−n(x
0
), we see
Q
∇u(x
0
)
(∇
2
u(x
0
)) =
∇
2
g(x
0
)0
00
.
Thus we obtain
˜
A
x
0
ζ =
∇
2
g(x
0
)ζ
0
,ζ
∈ R
N−1
with ζ =(ζ
,ζ
n
) ∈ R
N
. (1.4.16)
We shall calculate the mean curvature H at x
0
in the direction of n.Weplug
u in (1.4.9) to get
H =
div
∇
g
1+|∇
g|
2
(x
0
)+
∂
∂x
N
−1
1+|∇
g|
2
(x
0
)
=
div
∇
g
1+|∇
g|
2
(x
0
), (1.4.17)
where div
denotes the divergence in x
variables.
Axisymmetric surface. Suppose that Γ is obtained by rotating the graph of a
function ϕ(x
1
) around the x
1
-axis and that x
0
∈ Γ is not on the axis. Around
x
0
∈ Γ the hypersurface Γ is of form
Γ=
⎧
⎪
⎨
⎪
⎩
r = ϕ(x
1
); r =
⎛
⎝
N
j=2
x
2
j
⎞
⎠
1/2
⎫
⎪
⎬
⎪
⎭
.
If n is taken outward from x
1
-axis, i.e., n is given by (1.2.3), then Γ is given as
the zero level set of
u(x
1
,...,x
N
)=−r + ϕ(x
1
)
with n = −∇u/|∇u| (around x
0
). We obtain a formula for
˜
A
x
0
in terms of ϕ by
plugging above u into (1.4.5). However, we do not give its explicit formula. Here
we only calculate the mean curvature H at x
0
in the direction of n.Weplugu in
(1.4.9) and use the formula (1.2.3) to get
H =
∂
∂x
1
ϕ
x
1
(1 + ϕ
2
x
1
)
1/2
−
1
(1 + ϕ
2
x
1
)
1/2
N
j=2
∂
∂x
j
x
j
r
=
ϕ
x
1
x
1
(1 + ϕ
2
x
1
)
3/2
−
1
(1 + ϕ
2
x
1
)
1/2
N − 2
r
at x = x
0
=(x
01
,x
0
) (1.4.18)

32 Chapter 1. Surface evolution equations
where r = |x
| with x
=(x
2
,...,x
N
).
Gradient of normal vector fields Let n be a unit normal vector field of Γ around
x
0
.Letm be a (C
1
) extension of n to a tubular neighborhood of Γ around x
0
.
Since
A
x
0
τ = −((τ ·∇)m)(x
0
),
for τ ∈ T
x
0
Γ,
˜
A
x
0
ζ = −((Π
x
0
ζ ·∇)m)(x
0
)
= −((ζ ·∇)m)(x
0
)+ ζ,n(x
0
) (n(x
0
) ·∇)m(x
0
).
This implies that the matrix expression of
˜
A
x
0
(with respect to the standard
Euclidean basis) equals
−
∂
∂x
i
m
j
(x
0
)+n
i
(x)(n(x
0
) ·∇)m
j
(x
0
), 1 ≤ i, j ≤ N
(which should be symmetric since
˜
A
x
0
is symmetric). If the extension m has the
property that
((n(x
0
) ·∇)m)(x
0
)=0, (1.4.19)
then one may identify −∇m(x
0
)by
˜
A
x
0
. We shall use the notation ∇n by extend-
ing n to a tubular neighborhood of Γ around x
0
such that (1.4.19) holds. By this
interpretation −∇n =
˜
A
x
0
, so we shall often identify second fundamental form
A
x
0
with −∇n.
We conclude this section by studying the range of ∇n.LetS
N
denote the
space of all N × N real symmetric matrices.
Lemma 1.4.1. Let x
0
be a point in R
N
.Foreachp ∈ S
N−1
and X ∈ S
N
there is
a smooth hypersurface Γ around x
0
with the property that n(x
0
)=p, ∇n(x
0
)=
Q
p
(X),wheren isaunitnormalvectorfieldonΓ around x
0
and is extended to
a tubular neighborhood of Γ satisfying ((n(x
0
) ·∇)n)(x
0
)=0.
Proof. We may assume p =(0, 0,...,1) by rotation of coordinates and x
0
=0by
translation. The matrix Q
p
(X)isoftheform
⎛
⎜
⎝
0
Y
.
.
.
0 ··· 0
⎞
⎟
⎠
with Y ∈ S
N−1
.Weset
g(x
)=−
1
2
Yx
,x
for x
∈ R
N−1
to get g(0) = 0, ∇
g(0) = 0, ∇
2
g(0) = −Y .Since∇n(x
0
)=−
˜
A
x
0
, the formula
(1.4.16) yields
∇n(x
0
)=Q
p
(X).
1.5. Examples of surface evolution equations 33
1.5 Examples of surface evolution equations
We give general examples of equations of an evolving hypersurface whose normal
velocity V is determined by its normals and second fundamental forms. In general
such an evolution equation is of the form
V = f(x, t, n, ∇n)(1.5.1)
on an evolving hypersurface Γ
t
,wheref is a given function and n is a unit normal
vector field of Γ
t
. For consistency with the literature we take the negative of the
second fundamental form A of Γ
t
as an independent variable of f and denote it
by ∇n.HereV is the velocity in the direction of n.
1.5.1 General evolutions of isothermal interfaces
For an evolving hypersurface Γ
t
we consider
β(n)V = −a div
Γ
t
ξ(n)+c(x, t). (1.5.2)
Here ξ is the Cahn–Hoffman vector of a surface energy density γ
0
: S
N−1
→ (0, ∞)
and β is a given positive function on S
N−1
, a is a nonnegative constant and c is
a given function. We always assume that N ≥ 2ifa = 0 since the curvature term
equals zero when N = 1. As we observed in (1.4.15), this equation is an example of
(1.5.1). If c is independent of x and a = 1, (1.5.2) is often used to describe motion
of isothermal interface; there c is regarded as bulk free energy difference such as
temperature difference in both phases. The function 1/β is called the mobility.It
may be again anisotropic in the sense that it depends on the direction of normals.
The mobility is determined by microstructure of the hypersurface. Sometimes it
is proportional to γ
0
, i.e., βγ
0
is constant independent of n but in general 1/β is
not necessarily proportional to γ
0
. The equation (1.5.2) has an energy structure.
Indeed, we set
G(Γ) =
Γ
aγ
0
(n)dσ +
D
cdx (1.5.3)
for a hypersurface Γ surrounding D, then (1.5.2) is of the form
β(n)V = −δG/δΓ
t
where δG/δΓ
t
denotes the change ratio of (free energy) G per change of volume
of D in the direction of n.Heren is taken outward from D. In other words (1.5.2)
is a gradient flow of G.
Mean curvature flow equation. The equation (1.5.2) includes several interesting
important examples as a special case. If the mobility and the surface energy density
is isotropic with no driving force c and a = 1, then (1.5.2) becomes
V = H (1.5.4)
34 Chapter 1. Surface evolution equations
by rescaling time if necessary (or taking β ≡ γ
0
≡ 1, a =1,c = 0). This equation
is called the mean curvature flow equation.IfN =2sothatΓ
t
is a curve, (1.5.4)
is called the curve shortening equation.Ifκ denotes the curvature in the direction
of n, the curve shortening equation is of the form
V = κ. (1.5.5)
For the mean curvature flow equation the energy G in (1.5.3) is the surface area
of Γ. Thus (1.5.4) gives a deformation so that decrease ratio of area is steepest.
This is why (1.5.5) is called the curve shortening equation. Note that the equation
(1.5.4) is invariant under the change of orientation n. In other words the evolution
law (1.5.4) is the same even if we replace n by −n.
Hamilton–Jacobi equations. If a = 0, then (1.5.2) becomes
β(n)V = c(x, t). (1.5.6)
This equation is regarded as a special form of the Hamilton–Jacobi equation.
Indeed, if Γ
t
is represented by the graph of a function, i.e., x
N
= g(x
,t), then by
(1.1.2) and (1.2.2) the equation (1.5.6) is of the form
g
t
+ H(x
,t,g,∇
g)=0 (1.5.7)
with
H(x
,t,r,p
)=−c(x
,r,t)µ(p
)/β(−p
/µ(p
),µ(p
)
−1
),µ(p
)=(1+|p
|
2
)
1/2
.
The equation (1.5.7) is a first order equation and the curvature plays no role in
(1.5.6).
1.5.2 Evolution by principal curvatures
In the mean curvature flow equation the normal velocity depends only on principal
curvatures of hypersurfaces. There are several other examples of form
V = g(κ
1
,...,κ
N−1
; n), (1.5.8)
where g is a given function of principal curvatures of κ
1
,...,κ
N−1
and n.Inthe
mean curvature flow equation, g is independent of n and is taken as the first
elementary symmetric polynomial e
1
.
If g is taken as e
N−1
so that e
N−1
(κ
1
,...,κ
N−1
) equals the Gaussian curva-
ture K, (1.5.8) becomes the Gaussian curvature flow equation
V = K. (1.5.9)
Of course if N = 2, then this equation becomes the curve shortening equation
V = κ. More generally, for each 1 ≤ m ≤ N − 1,
V = H
m
(1.5.10)

1.5. Examples of surface evolution equations 35
is called the m-th symmetric curvature flow equation,whereH
m
is the m-th sym-
metric curvature e
m
(κ
1
,...,κ
N−1
). The equation
V = H
N−1
/H
N−2
(N ≥ 3) (1.5.11)
is called the harmonic curvature flow equation, which is a special case of
V = H
m
/H
. (1.5.12)
All equations (1.5.9)-(1.5.12) are examples of (1.5.8). As we see later, we impose
the restriction <min (1.5.12) so that the equation is parabolic at least for convex
surfaces. Note that in general the evolution law (1.5.9) or (1.5.10) (with even m)
may depend on the choice of orientation n. For a closed evolving hypersurface Γ
t
we take the inward normal vector field as n so that the sphere shrinks as time
develops. The same remark applies to (1.5.12). We use this convention when we
consider the evolution by principle curvatures (1.5.10) with even m and (1.5.12)
with even m − .
1.5.3 Other examples
In general the right-hand side of (1.5.2) is not proportional to the velocity. A
natural generalization is
V = h(−a div
Γ
t
ξ(n)+c, n)(1.5.13)
where h is nondecreasing in the first variable and h(0, n)=0.IfN =2sothatΓ
t
is a curve in the plane and h(σ, n)=σ
1/3
+
with c =0,a =1,γ
0
≡ 1, then (1.5.13)
becomes
V =(κ
+
)
1/3
(1.5.14)
where σ
+
=max(σ, 0). The equation (1.5.14) is called the affine curvature flow
equation since the equation is invariant under affine transformation.
1.5.4 Boundary conditions
It often happens that a hypersurface Γ
t
moves in a domain Ω in R
N
and the
geometric boundary of Γ
t
intersects the boundary ∂Ω of Ω. In this case in addition
to the equation (1.5.1) in Ω we have to impose the boundary condition so that
evolution is determined by equations. We give here typical examples of them. We
assume that the boundary ∂ΩisatleastaC
1
hypersurface in R
N
.Letν be the
unit normal vector field of ∂ΩoutwardfromΩ.Letn be the unit normal vector
field of a smooth hypersurface {Γ
t
} in Ω.
Neumann boundary condition. This condition imposes
ν, n =0

36 Chapter 1. Surface evolution equations
on the intersection of Γ
t
and ∂Ω. Geometrically speaking, Γ
t
intersects ∂Ω orthog-
onally, i.e., Γ
t
⊥∂Ω.
Prescribed contact angle boundary condition. Let z be a given real-valued contin-
uous function on ∂Ω that satisfies |z| < 1on∂Ω. The prescribed contact boundary
condition imposes
ν, n = z
on the intersection of Γ
t
and ∂Ω. Of course if z = 0, this condition is exactly
the Neumann boundary condition. Although the orientation of Γ
t
is irrelevant to
describe the Neumann boundary condition, the prescribed angle condition depends
on the orientation of Γ
t
. In the literature the prescribed contact angle condition
is often referred to as the Neumann boundary condition.
:
cosz
T
n
O
T
Figure 1.3: Prescribed contact angle
Dirichlet boundary condition. Let S be a given codimension 2-closed surface in
R
N
. The Dirichlet condition imposes that the geometric boundary of Γ
t
always
equals S. This condition is so far not easy to treat in a level set method so we do
not discuss this problem much in this book.
1.6 Level set equations
For a given surface evolution equation we shall introduce its level set equation.
We shall study various properties of level set equations.
1.6.1 Examples
We consider a surface evolution equation
V = f(x, t, n, ∇n)(1.6.1)
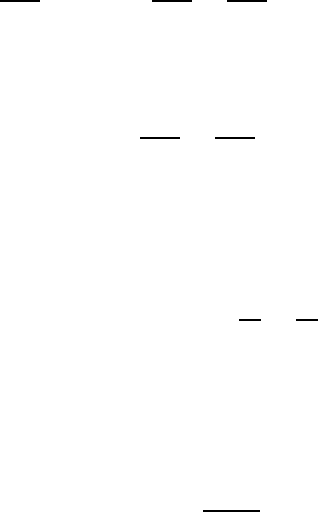
1.6. Level set equations 37
on an evolving hypersurface Γ
t
in a domain Ω in R
N
.Heref(x, t, ·, ·)for
(x, t) ∈ Ω × [0,T] is a given real-valued function defined in
E = {(p, Q
p
(X)); p ∈ S
N−1
,X∈ S
N
}.
By Lemma 1.4.1 the set E is a natural space so that (n, ∇n) lives. We say an
equation
u
t
(x, t)+F (x, t, ∇u(x, t), ∇
2
u(x, t)) = 0 for all (x, t) ∈ Ω × (0,T)(1.6.2)
is a level set equation of (1.6.1) if for each level set
Γ
t
= {x; u(x, t)=constant}
of a C
2,1
solution u of (1.6.2) near (x
0
,t
0
) ∈ Ω satisfies (1.6.1) at (x
0
,t
0
)provided
that ∇u(x
0
,t
0
) = 0 and that the orientation n is chosen so that n(x
0
,t
0
)=
−∇u(x
0
,t
0
) /|∇u(x
0
,t
0
)|,wherex
0
∈ Γ
t
0
.HereF is a real-valued function defined
in Ω × [0,T] × (R
N
\{0}) × S
N
.
Such an equation is uniquely determined by (1.6.1). Indeed, using the level
set representation of V,n and ∇n, (1.6.1) is of form
u
t
|∇u|
= f
x, t, −
∇u
|∇u|
, −
1
|∇u|
Q
∇u
(∇
2
u)
on the evolving hypersurface. The representation of V,n and ∇n is the same if the
hypersurface is a c-level set instead of the zero level set of u.Thus,theequation
u
t
−|∇u|f
x, t, −
∇u
|∇u|
, −
1
|∇u|
Q
∇u
(∇
2
u)
=0
is the unique level set equation. It may be rewritten as
u
t
+ F
f
(x, t, ∇u, ∇
2
u)=0 (1.6.3)
with
F
f
(x, t, p, X)=−|p|f
x, t, −
p
|p|
, −
1
|p|
Q
p
(X)
(1.6.4)
for p ∈ R
N
\{0}, X ∈ S
N
,(x, t) ∈ Ω × [0,T]. Note that the function F
f
is not
defined for p = 0 in general as we will see in following examples.
Level set mean curvature flow equation. If (1.6.1) is the mean curvature flow
equation (1.5.4) : V = H, then by (1.2.1) and (1.4.6), the level set equation is
u
t
− ∆u +
1≤i, j≤N
u
x
i
u
x
j
|∇u|
2
u
x
i
x
j
=0 (1.6.5)
