Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

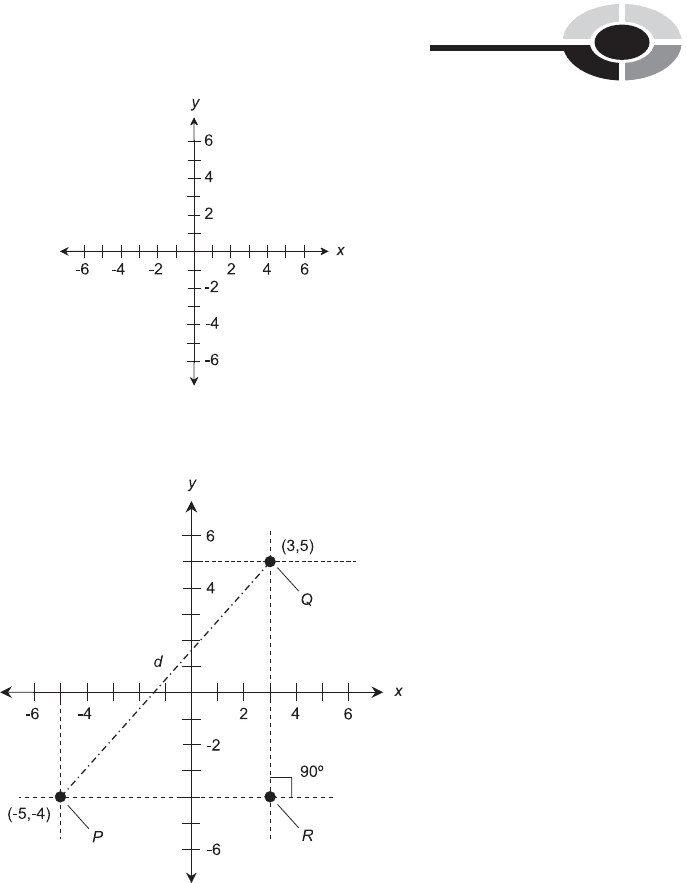
ORDERED PAIRS AS POINTS

Figure 11-2 shows two speciﬁc points P and Q on the Cartesian plane. Any

given point on the plane can be denoted as an ordered pair in the form (x,y),

determined by the numerical values at which perpendiculars from the point

intersect the x and y axes. The coordinates of point P are (–5,–4), and the

coordinates of point Q are (3,5). In Fig. 11-2, the perpendiculars are

Fig. 11-1. The Cartesian plane is deﬁned by two number lines that intersect at right angles.

Fig. 11-2. Two points P and Q, plotted in rectangular coordinates, and a third point R,

important in ﬁnding the distance d between P and Q.

CHAPTER 11 Graphing It 251

shown as horizontal and vertical dashed lines. When denoting an ordered

pair, it is customary to place the two numbers or variables together right

up against the comma; there is no space after the comma.

The word ‘‘ordered’’ means that the order in which the numbers are listed

is important. The ordered pair (7,2) is not the same as the ordered pair (2,7),

even though both pairs contain the same two numbers. In this respect,

ordered pairs are diﬀerent than mere sets of numbers. Think of a two-lane

highway with a northbound lane and a southbound lane. If there is never any

traﬃc on the highway, it doesn’t matter which lane (the one on the eastern

side or the one on the western side) is called ‘‘northbound’’ and which is

called ‘‘southbound.’’ But when there are vehicles on that road, it makes a

big diﬀerence! The untraveled road is like a set; the traveled road is like an

ordered pair.

ABSCISSA, ORDINATE, AND ORIGIN

In any graphing scheme, there is at least one independent variable and at

least one dependent variable. You learned about these types of variables in

Chapter 2. The independent-variable coordinate (usually x) of a point on

the Cartesian plane is called the abscissa, and the dependent-variable coordi-

nate (usually y) is called the ordinate. The point where the two axes intersect,

in this case (0,0), is called the origin. In the scenario shown by Fig. 11-2,

point P has an abscissa of –5 and an ordinate of –4, and point Q has an

abscissa of 3 and an ordinate of 5.

DISTANCE BETWEEN POINTS

Suppose there are two diﬀerent points P ¼ (x

) and Q ¼ (x

) on the

Cartesian plane. The distance d between these two points can be found by

determining the length of the hypotenuse, or longest side, of a right

triangle PQR , where point R is the intersection of a ‘‘horizontal’’ line through

P and a ‘‘vertical’’ line through Q. In this case, ‘‘horizontal’’ means ‘‘parallel

to the x axis,’’ and ‘‘vertical’’ means ‘‘parallel to the y axis.’’ An example

is shown in Fig. 11-2. Alternatively, we can use a ‘‘horizontal’’ line through

Q and a ‘‘vertical’’ line through P to get the point R. The resulting right

triangle in this case has the same hypotenuse, line segment PQ, as the triangle

determined the other way.

The Pythagorean theorem from plane geometry states that the square of

the length of the hypotenuse of a right triangle is equal to the sum of the

squares of the other two sides. In the Cartesian plane, that means the

PART 3 Shapes and Places

252

following equation always holds true:

¼ðx

 x

þðy

 y

and therefore:

d ¼½ðx

 x

þðy

 y



1=2

where the 1/2 power is the square root. In the situation shown in Fig. 11-2,

the distance d between points P ¼ (x

) ¼ (–5,–4) and Q ¼ (x

) ¼ (3,5),

rounded to two decimal places is:

d ¼f½3 ð5Þ

þ½5 ð4Þ

1=2

¼½ð3 þ 5Þ

þð5 þ 4Þ



1=2

¼ð8

þ 9

1=2

¼ð64 þ 81Þ

1=2

¼ 145

1=2

¼ 12:04

PROBLEM 11-1

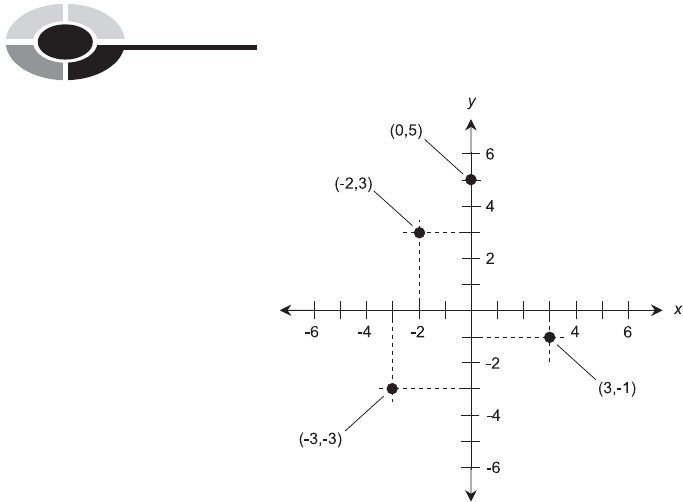
Plot the following points on the Cartesian plane: (2,3), (3,1), (0,5), and

(3,3).

SOLUTION 11-1

These points are shown in Fig. 11-3. The dashed lines are perpendiculars,

dropped to the axes to show the x and y coordinates of each point.

(The dashed lines are not part of the coordinates themselves.)

PROBLEM 11-2

What is the distance between (0,5) and (3,3) in Fig. 11-3? Express the

answer to three decimal places.

SOLUTION 11-2

Use the distance formula. Let (x

) ¼ (0,5) and (x

) ¼ (3,3). Then:

d ¼½ðx

 x

þðy

 y



1=2

¼ ½ð3  0Þ

þð3  5Þ



1=2

¼ ½ð3Þ

þð8Þ



1=2

¼ð9 þ 64Þ

1=2

¼ 73

1=2

¼ 8:544

CHAPTER 11 Graphing It 253

Straight Lines in the Cartesian Plane

In Chapter 6, we saw what the graphs of quadratic equations look like in

the Cartesian plane; they appear as parabolas. Here, we’ll take a detailed

look at how straight lines are plotted on the basis of linear equations in

two variables. The standard form for this type of equation is as follows:

ax þ by þ c ¼ 0

where a, b, and c are real-number constants, and the variables are x and y.

SLOPE–INTERCEPT FORM

A linear equation in variables x and y can be manipulated so it is in a form

that is easy to plot on the Cartesian plane. Here is how a two-variable linear

equation in standard form can be converted to slope–intercept form:

ax þ by þ c ¼ 0

ax þ by ¼c

by ¼ax  c

y ¼ða=bÞx  c=b

y ¼ða=bÞx þðc=bÞ

Fig. 11-3. Illustration for Problems 11-1 and 11-2.

PART 3 Shapes and Places

254

where a, b, and c are real-number constants (the coeﬃcients of the equation),

and b 6¼ 0. The quantity –a/b is called the slope of the line, an indicator of

how steeply and in what sense the line slants. The quantity –c/b represents

the y value of the point at which the line crosses the y axis; this is called

the y-intercept.

Let dx represent an arbitrarily small change in the value of x on such a

graph. Let dy represent the tiny change in the value of y that results from

this tiny change in x. The limit of the ratio dy/dx, as both dx and dy approach

0, is the slope of the line.

Suppose m is the slope of a line in Cartesian coordinates, and k is the

y-intercept. The linear equation of that line can be written in slope–intercept

form as:

y ¼ða=bÞx þðc=bÞ

and therefore:

y ¼ mx þ k

To plot a graph of a linear equation in Cartesian coordinates using the

slope–intercept form, proceed as follows:

Convert the equation to slope–intercept form.

Plot the point x ¼ 0, y ¼ k.

Move to the right by n units on the graph.

If m is positive, move upward mn units.

If m is negative, move downward |m|n units, where |m| is the absolute

value of m.

If m ¼ 0, don’t move up or down at all.

Plot the resulting point x ¼ n, y ¼ mn þ k.

Connect the two points with a straight line.

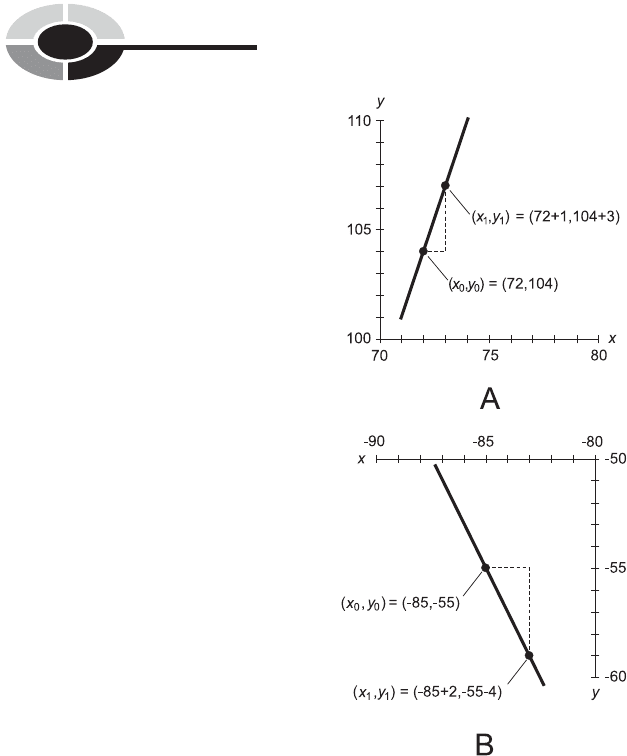
Figures 11-4A and B illustrate the following linear equations as graphed

in slope–intercept form:

y ¼ 5x  3

y ¼x þ 2

A positive slope indicates that the line ramps upward as you move from left

to right, and a negative slope indicates that the line ramps downward as you

move from left to right. A slope of 0 indicates a horizontal line. The slope of a

vertical line is undeﬁned because, in the form shown here, it requires that m

be deﬁned as a quotient in which the denominator is equal to 0.

CHAPTER 11 Graphing It 255

Fig. 11-4. (A) Graph of the linear equation y ¼ 5x  3. (B) Graph of the linear

equation y ¼ –x þ 2.

PART 3 Shapes and Places

256

POINT–SLOPE FORM

It is diﬃcult to plot a graph of a line based on the y-intercept (the point at

which the line intersects the y axis) when the part of the graph of interest

is far from the y axis. In this sort of situation, the point–slope form of a linear

equation can be used. This form is based on the slope m of the line and

the coordinates of a known point (x

y  y

¼ mðx  x

To plot a graph of a linear equation using the point–slope method, follow

these steps in order:

Convert the equation to point–slope form.

Determine a point (x

) by ‘‘plugging in’’ values.

Plot (x

) on the coordinate plane.

Move to the right by n units on the graph, where n is some number

that represents a reasonable distance on the graph.

If m is positive, move upward mn units.

If m is negative, move downward |m|n units, where |m| is the absolute

value of m.

If m ¼ 0, don’t move up or down at all.

Plot the resulting point (x

Connect the points (x

) and (x

) with a straight line.

Figure 11-5A illustrates the following linear equation as graphed in

point–slope form:

y  104 ¼ 3ðx  72Þ

Figure 11-5B is a graph of another linear equation in point–slope form:

y þ 55 ¼2ðx þ 85Þ

FINDING A LINEAR EQUATION BASED ON TWO POINTS

Suppose we are working in the Cartesian plane, and we know the exact

coordinates of two points P and Q. These two points deﬁne a unique and

distinct straight line. Call the line L. Let’s give the coordinates of the points

these names:

P ¼ðx

ó y

Q ¼ðx

ó y

CHAPTER 11 Graphing It 257

The slope m of line L can be found using either of the following formulas:

m ¼ðy

 y

Þ=ðx

 x

m ¼ðy

 y

Þ=ðx

 x

These formulas work provided x

is not equal to x

. (If x

¼ x

, the denomi-

nators are equal to 0.) The point–slope equation of the line L can be

determined based on the known coordinates of P or Q. Therefore, either

of the following formulas represent the line L:

y  y

¼ mðx  x

y  y

¼ mðx  x

Fig. 11-5. (A) Graph of the linear equation y  104 ¼ 3(x  72). (B) Graph of the linear

equation y þ 55 ¼ –2(x þ 85).

PART 3 Shapes and Places

258

Reduced to standard form, these equations become:

mx  y þðy

 mx

Þ¼0

mx  y þðy

 mx

Þ¼0

That is, the coeﬃcients a, b, and c are:

a ¼ m

b ¼1

c ¼ y

 mx

¼ y

 mx

FINDING A LINEAR EQUATION BASED ON

y-INTERCEPT AND SLOPE

Suppose we are shown, on a graph, the coordinates of the point at which a

straight line L crosses the y axis, and also the slope of that line. This informa-

tion is suﬃcient to uniquely deﬁne the equation of L. Let’s say that the

y-intercept is equal to y

and the slope of the line is equal to m. Then the

equation of the line is:

y  y

¼ mx

Reduced to standard form, this becomes:

mx  y þ y

¼ 0

That is, the coeﬃcients a, b, and c are:

a ¼ m

b ¼1

c ¼ y

PROBLEM 11-3

Suppose you are shown Fig. 11-6. What is the equation of this line in

standard form?

SOLUTION 11-3

The slope of the line is equal to 2; we are told this in the graph. Therefore,

m ¼ 2. The y-intercept is 4, so y

¼ 4. This means the equation of the line is:

2x  y þ 4 ¼ 0

CHAPTER 11 Graphing It 259

The Polar Coordinate Plane

Two versions of the polar coordinate plane are shown in Figs. 11-7 and 11-8.

The independent variable is plotted as an angle  (THAY-tuh) relative to a

reference axis pointing to the right (or ‘‘east’’), and the dependent variable

is plotted as a distance (called the radius) r from the origin. (The origin

is the center of the graph where r ¼ 0.) A coordinate point is thus denoted

in the form of an ordered pair ( , r). In some texts, the independent and

dependent variables are reversed, and the resulting ordered pairs are in the

form (r, ). But intuitively, it makes more sense to most people to plot

the radius as a function of the angle, and not to plot the angle as a function

of the radius. Here, we’ll use the form (, r).

THE RADIUS

In any polar plane, the radii are shown by concentric circles. The larger the

circle, the greater the value of r. In Figs. 11-7 and 11-8, the circles are not

labeled in units. You can do that for yourself. Imagine each concentric circle,

working outward, as increasing by any number of units you want. For exam-

ple, each radial division might represent one unit, or ﬁve units, or 10, or 100.

THE DIRECTION

In polar coordinates, the direction can be expressed in angular degrees

(symbolized 8, where a full circle represents 3608) or in units called radians.

Fig. 11-6. Illustration for Problem 11-3.

PART 3 Shapes and Places

260