Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

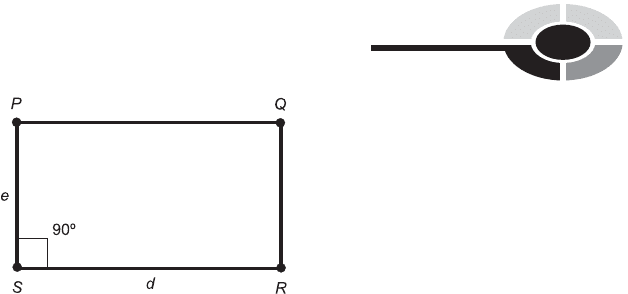
PERIMETER OF RECTANGLE

Suppose we have a rectangle deﬁned by four distinct points P, Q, R, and S,in

which two adjacent sides have lengths d and e as shown in Fig. 9-31. Let d

be the base length, and let e be the height. Then the perimeter, B, of the

rectangle is given by the following formula:

B ¼ 2d þ 2e

INTERIOR AREA OF RECTANGLE

Suppose we have a rectangle as deﬁned above and in Fig. 9-31. The interior

area, A, is given by:

A ¼ de

PERIMETER OF SQUARE

Suppose we have a square deﬁned by four distinct points P, Q, R, and S, and

having sides all of which have the same length. The square is a special case

of the rectangle (Fig. 9-31), in which d ¼ e. Suppose the lengths of all four

sides are equal to d. The perimeter, B, of this square is given by the following

formula:

B ¼ 4d

INTERIOR AREA OF SQUARE

Suppose we have a square as deﬁned above and in Fig. 9-31. The interior

area, A, is given by:

A ¼ d

Fig. 9-31. Perimeter and area of a rectangle. If d ¼ e, the ﬁgure is a square.

CHAPTER 9 Geometry on the Flats 221

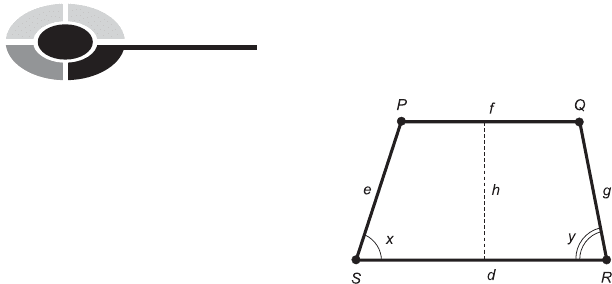
PERIMETER OF TRAPEZOID

Imagine a trapezoid deﬁned by four distinct points P, Q, R, and S, and

having sides of lengths d, e, f, and g as shown in Fig. 9-32. Let d be the

base length, let h be the height, let x be the measure of the angle between

the sides having length d and e, and let y be the measure of the angle between

the sides having length d and g. Suppose the sides having length d and f

(line segments RS and PQ) are parallel. Then the perimeter, B, of the

trapezoid is:

B ¼ d þ e þ f þ g

INTERIOR AREA OF TRAPEZOID

Suppose we have a trapezoid as deﬁned above and in Fig. 9-32. The interior

area, A, is equal to the product of the height and the average of the lengths

of the base and the top. Here is the formula:

A ¼ðdh þ fhÞ=2

PROBLEM 9-5

Suppose a room has a north-facing wall that is rectangular, and that has

a rectangular window in the center. The room measures 5.00 m from east-

to-west, and the ceiling is 2.60 m high. The window, measured at its outer

frame, measures 1.45 m high by 1.00 m wide. What is the surface area of

the wall, not including the window?

SOLUTION 9-5

First, determine the area of the wall including the area of the window.

If we call this area A

wall

, then

wall

¼ 5:00  2:60

¼ 13:00 m

Fig. 9-32. Perimeter and area of a trapezoid.

PART 3 Shapes and Places

222

The area of the window (call it A

win

), measured at its outer frame, is:

win

¼ 1:45  1:00

¼ 1:45 m

Let A be the area of the wall, not including the window. Then

A ¼ A

wall

 A

win

¼ 13:00  1:45

¼ 11:55 m

PROBLEM 9-6

Suppose a plot of land is shaped like a parallelogram. Adjacent sides measure

500 m and 400 m. What is the perimeter of this plot of land? What is its inter-

ior area?

SOLUTION 9-6

The perimeter of the plot of land is equal to the sum of twice the lengths of

the adjacent sides. Suppose we call the lengths of the sides d and e, where

d ¼ 500 m and e ¼ 400 m. Then the perimeter B, in meters, is:

B ¼ 2d þ 2e

¼ 2  500 þ 2  400

¼ 1000 þ 800

¼ 1800 m

In order to calculate the area of the ﬁeld, we must know how wide it is.

For ﬁxed lengths of sides, the width of a parallelogram depends on

the angle between two adjacent sides (in this case, boundaries of the ﬁeld).

We aren’t given this information, so we can’t determine the area of the ﬁeld.

Circles and Ellipses

That’s enough of ﬁgures with straight lines. Let’s get into plane curves.

In some ways, the following formulas are easier for mathematicians to derive

than the ones for ﬁgures consisting of lines and angles.

CHAPTER 9 Geometry on the Flats 223

PERIMETER OF CIRCLE

Suppose we have a circle having radius r as shown in Fig. 9-33. Then the

perimeter, B, also called the circumference, of the circle is given by the

following formula:

B ¼ 2pr

INTERIOR AREA OF CIRCLE

Suppose we have a circle as deﬁned above and in Fig. 9-33. The interior area,

A, of the circle can be found using this formula:

A ¼ pr

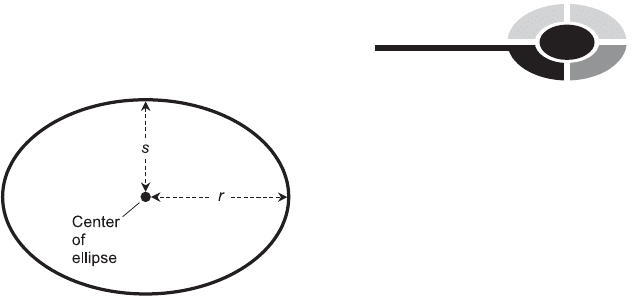
INTERIOR AREA OF ELLIPSE

Suppose we have an ellipse whose major half-axis (the longer half-axis or

largest radius) measures r, and whose minor half-axis (the shorter half-axis

or smallest radius) measures s as shown in Fig. 9-34. The interior area, A,

of the ellipse is given by:

A ¼ prs

PROBLEM 9-7

What is the circumference of a circle whose radius is 10.0000 m? What is its

interior area?

Fig. 9-33. Perimeter and area of a circle.

PART 3 Shapes and Places

224

SOLUTION 9-7

In this case, r ¼ 10.0000, expressed in meters. To calculate the circumference

B in meters, proceed as follows. Consider the value of p to be 3.14159.

B ¼ 2pr

¼ 2  3:14159  10:0000

¼ 62:8318 m

To calculate the interior area A in square meters, proceed as follows:

A ¼ pr

¼ 3:14159  10

¼ 314:59 m

PROBLEM 9-8

Consider an ellipse whose minor half-axis is 10.0000 m and whose major

half-axis can be varied at will. What must the major half-axis be in order

to get an interior area of 200.000 m

? Consider the value of p to be 3.14159.

SOLUTION 9-8

In this problem, A ¼ 200 and r ¼ 10. We seek to ﬁnd the value of s in this

formula:

A ¼ prs

Substituting the values in, the calculation goes like this:

200:000 ¼ 3:14159  10:0000  s

10:0000  s ¼ 200:000=3:14159

s ¼ 6:36620 m

Fig. 9-34. Interior area of an ellipse.

CHAPTER 9 Geometry on the Flats 225

Quiz

Refer to the text in this chapter if necessary. A good score is eight correct.

Answers are in the back of the book.

1. In an equilateral plane triangle, each interior angle

(a) has a measure less than 608

(b) has a measure greater than 608

(d) has a measure diﬀerent from either of the other two angles

2. Suppose a building is constructed in the shape of a parallelogram,

rather than in the usual rectangular shape, because of the strange

layout of streets in that part of town. The sides of the building run

east–west and more or less northeast–southwest. The length of the

building measured along the east–west walls is 30 m, and the distance

between the northerly east–west end and the southerly east–west end is

40 m. What is the area of the basement ﬂoor (including the area taken

up by interior and exterior walls)?

(a) 1500 m

(b) 1200 m

(d) More information is needed to answer this question.

3. Suppose a building is constructed in the shape of a parallelogram,

rather than in the usual rectangular shape, because of the strange

layout of streets in that part of town. The sides of the building run

east–west and more or less northeast–southwest. The length of the

building measured along the east–west walls is 30 m, and the length

measured along the northeast–southwest walls is 40 m. What is the

area of the basement ﬂoor (including the area taken up by interior

and exterior walls)?

(a) 1500 m

(b) 1200 m

(d) More information is needed to answer this question.

4. If the radius of a circle is quadrupled, what happens to its interior area?

(a) It becomes twice as great.

(b) It becomes four times as great.

(d) More information is needed to answer this question.

PART 3 Shapes and Places

226

5. If the length of the minor semi-axis of an ellipse is quadrupled while

the length of the major semi-axis is cut in half, what happens to the

interior area?

(a) It stays the same.

(b) It increases by a factor of the square root of 2.

(d) It increases by a factor of 4.

6. A right plane triangle cannot

(a) be an isosceles triangle

(b) have three sides all of diﬀerent lengths

(d) have any interior angle measuring less than 908

7. Suppose three towns, called Jimsville, Joesville, and Johnsville, all lie

along a perfectly straight, east–west stretch of highway called Route

999. As you drive from west to east, you encounter Jimsville ﬁrst,

then Joesville, and then Johnsville. Suppose the distance between

Jimsville and Joesville is 8 kilometers (km), and the distance between

Joesville and Johnsville is 6 km. What is the distance between Jimsville

and Johnsville as measured along Route 999?

(a) 8 km

(b) 10 km

(d) More information is needed to answer this question.

8. Suppose Jimsville and Johnsville lie along a perfectly straight, east–

west stretch of highway called Route 999. Joesville lies north of

Route 999, and is in a position such that it is 8 km away from

Jimsville and 6 km away from Johnsville. Suppose a straight line

connecting Jimsville and Joesville is perpendicular to a straight line

connecting Johnsville and Joesville. What is the distance between

Jimsville and Johnsville as measured along Route 999?

(a) 8 km

(b) 10 km

(d) More information is needed to answer this question.

9. Suppose Jimsville and Johnsville lie along a perfectly straight, east–

west stretch of highway called Route 999. Joesville lies south of

Route 999, and is in a position such that it is 8 km away from

Jimsville and 8 km away from Johnsville. All three towns lie at the

CHAPTER 9 Geometry on the Flats 227

vertices of an isosceles triangle. What is the distance between

Jimsville and Johnsville as measured along Route 999?

(a) 8 km

(b) 10 km

(d) More information is needed to answer this question.

10. Suppose Jimsville and Johnsville lie along a perfectly straight, east–

west stretch of highway called Route 999. Joesville lies south of

Route 999, and is in a position such that it is 8 km away from

Jimsville and 8 km away from Johnsville. All three towns lie at the

vertices of an equilateral triangle. What is the distance between

Jimsville and Johnsville as measured along Route 999?

(a) 8 km

(b) 10 km

(d) More information is needed to answer this question.

PART 3 Shapes and Places

228

CHAPTER

Geometry in Space

Solid geometry involves points, lines, and planes. The diﬀerence between two-

dimensional (2D) geometry and three-dimensional (3D) geometry is the fact

that, well, there’s an extra dimension! This makes things more interesting,

and also more complicated.

Points, Lines, and Planes

A point can be envisioned as an inﬁnitely tiny sphere, having height, width,

and depth all equal to zero, but nevertheless possessing a speciﬁc location.

A point is zero-dimensional (0D). A line can be thought of as an inﬁnitely

thin, perfectly straight, inﬁnitely long thread or wire. It is one-dimensional

(1D). A plane can be imagined as an inﬁnitely thin, perfectly ﬂat surface

having an inﬁnite expanse. It is two-dimensional (2D). Space in the simplest

sense is the set of points representing all possible physical locations in the

universe at any speciﬁc instant in time. Space is three-dimensional (3D).

229

If time is included in a concept of space, we get four-dimensional (4D) space,

also known as hyperspace.

NAMING POINTS, LINES, AND PLANES

Points, lines, and planes in solid geometry are usually named using upper-

case, italicized letters of the alphabet, just as they are in plane geometry.

A common name for a point is P (for ‘‘point’’). A common name for a

line is L (for ‘‘line’’). When it comes to planes in 3D space, we must use

our imaginations. The letters X, Y, and Z are good choices. Sometimes lower-

case, non-italic letters are used, such as m and n.

When we have two or more points, the letters immediately following P

are used, for example Q, R, and S. If two or more lines exist, the letters

immediately following L are used, for example M and N. Alternatively,

numeric subscripts can be used. We might have points called P

, P

, and

so forth, lines called L

, L

, and so forth, and planes called X

, X

and so forth.

THREE POINT PRINCIPLE

Suppose that P, Q, and R are three diﬀerent geometric points, no two

of which lie on the same line. Then these points deﬁne one and only one

(a unique or speciﬁc) plane X. The following two statements are always

true, as shown in Fig. 10-1:

P, Q, and R lie in a common plane X.

X is the only plane in which all three points lie.

In order to show that a surface extends inﬁnitely in 2D, we have to be

imaginative. It’s not as easy as showing that a line extends inﬁnitely in

1D, because there aren’t any good ways to draw arrows on the edges of

a plane region the way we can draw them on the ends of a line segment.

Fig 10-1. Three points P, Q, and R, not all on the same line, deﬁne a speciﬁc plane X.

The plane extends inﬁnitely in 2D.

PART 3 Shapes and Places

230