Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

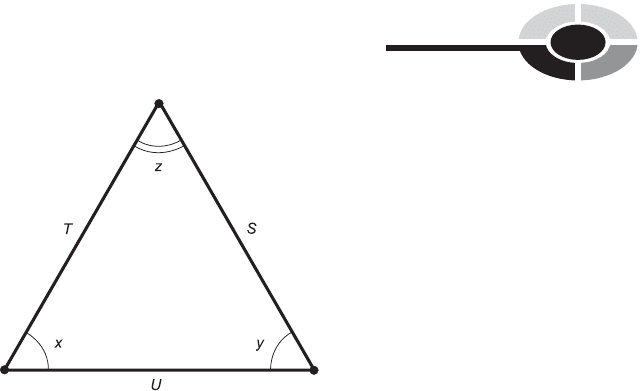
of the interior angles be x, y, and z. The following equation holds if the

angular measures are given in degrees:

x þ y þ z ¼ 180



ISOSCELES TRIANGLE

Suppose we have a triangle with sides S, T, and U, having lengths s, t, and u.

Let x, y, and z be the angles opposite S, T, and U respectively (Fig. 9-19).

Suppose any of the following equations hold:

s ¼ t

t ¼ u

s ¼ u

x ¼ y

y ¼ z

x ¼ z

Then the triangle is an isosceles triangle, and the following logical statements

are true:

If s ¼ t then x ¼ y

If t ¼ u then y ¼ z

If s ¼ u then x ¼ z

If x ¼ y then s ¼ t

If y ¼ z then t ¼ u

If x ¼ z then s ¼ u

Fig. 9-19. Isosceles and equilateral triangles.

CHAPTER 9 Geometry on the Flats 211

EQUILATERAL TRIANGLE

Suppose we have a triangle with sides S, T, and U, having lengths s, t, and u.

Let x, y, and z be the angles opposite S, T, and U respectively (Fig. 9-19).

Suppose either of the following are true:

s ¼ t ¼ u

x ¼ y ¼ z

Then the triangle is said to be an equilateral triangle, and the following

logical statements are valid:

If s ¼ t ¼ u then x ¼ y ¼ z

If x ¼ y ¼ z then s ¼ t ¼ u

That is, all equilateral triangles have precisely the same shape; they are all

similar. They are not necessarily all the same size, however.

THEOREM OF PYTHAGORAS

Suppose we have a right triangle deﬁned by points P, Q, and R whose

sides are D, E, and F having lengths d, e, and f, respectively. Let f be the

side opposite the right angle (Fig. 9-20). Then the following equation is

always true:

þ e

¼ f

The converse of this is also true: If there is a triangle whose sides have

lengths d, e, and f, and the above equation is true, then that triangle is a

right triangle.

The longest side of a right triangle is always the side opposite the right

angle, and is called the hypotenuse. The above formula can be stated verbally

as follows: ‘‘The square of the length of the hypotenuse of a right triangle

Fig. 9-20. The Theorem of Pythagoras.

PART 3 Shapes and Places

212

is equal to the sum of the squares of the lengths of the other two sides.’’ This

is called the Theorem of Pythagoras or the Pythagorean Theorem.Itis

named after a Greek geometer, Pythagoras of Samos, who lived in the 4th

century B.C.

PERIMETER OF TRIANGLE

Suppose we have a triangle deﬁned by points P, Q, and R, and having sides S,

T, and U of lengths s, t, and u, as shown in Fig. 9-21. Let s be the base length,

h be the height, and x be the angle between the sides having length s and t.

Then the perimeter, B, of the triangle is given by the following formula:

B ¼ s þ t þ u

INTERIOR AREA OF TRIANGLE

Consider the same triangle as deﬁned above; refer again to Fig. 9-21.

The interior area, A, can be found with this formula:

A ¼ sh=2

PROBLEM 9-3

What is the interior area of a triangle whose base is 4 meters (m) long and

whose height is 2 m?

SOLUTION 9-3

In this case, the length s is 4 (in meters) and the height h is 2 (also in meters).

Therefore, the area (in square meters or m

) is:

A ¼ sh=2

¼ 4  2=2

¼ 4m

Fig. 9-21. Perimeter and area of triangle.

CHAPTER 9 Geometry on the Flats 213

PROBLEM 9-4

If the height and the base length of a triangle are both doubled, what happens

to the interior area?

SOLUTION 9-4

The interior area quadruples. Let’s prove this for the general case. Let

the initial base length be s

and the initial height be h

. Let the ﬁnal base

length, s

,be2s

(twice the initial base length) and the ﬁnal height, h

,be

(twice the initial height):

¼ 2s

¼ 2h

Then the initial area, A

, is:

¼ s

The ﬁnal area, A

, is:

¼ s

¼ð2s

Þð2h

Þ=2

¼ 4ðs

=2Þ

¼ 4A

This shows that doubling both the base length and the height of a triangle

causes its interior area to increase by a factor of 4. Interestingly, this is

true even if the shape of the triangle changes in the process of the base-length

and height change. As long as the constraints are met (doubling of both the

base length and the height), it doesn’t matter if, or how much, the triangle

is ‘‘stretched horizontally’’; the interior area will increase by the same factor

regardless.

Quadrilaterals

A four-sided geometric ﬁgure that lies in a single plane is called a quadrilat-

eral. There are several classiﬁcations, and various formulas that apply to

each.

PART 3 Shapes and Places

214

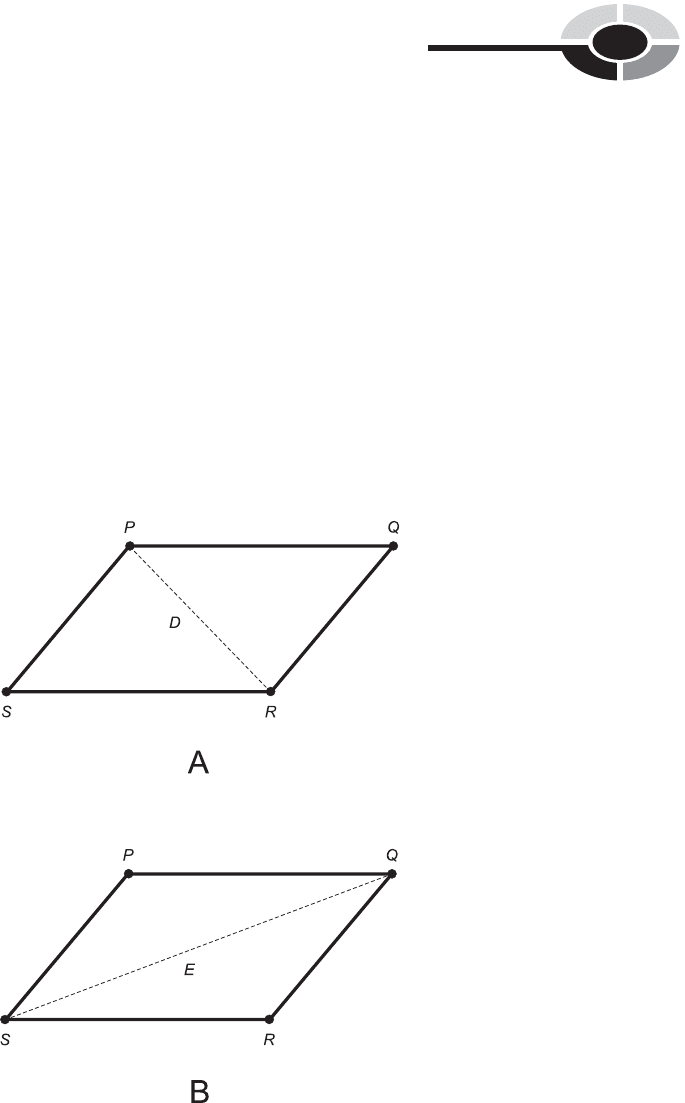
PARALLELOGRAM DIAGONALS

Suppose we have a parallelogram deﬁned by four distinct points P, Q, R,

and S. Let D be a straight line segment connecting P and R as shown in

Fig. 9-22A. Then D is a minor diagonal of the parallelogram, and the triangles

deﬁned by D are congruent:

PQR ﬃ RSP

Let E be a line segment connecting Q and S (Fig. 9-22B). Then E is a

major diagonal of the parallelogram, and the triangles deﬁned by E are

congruent:

QRS ﬃ SPQ

Fig. 9-22. Triangles deﬁned by the minor diagonal (A) or the major diagonal (B) of a

parallelogram are congruent.

CHAPTER 9 Geometry on the Flats 215

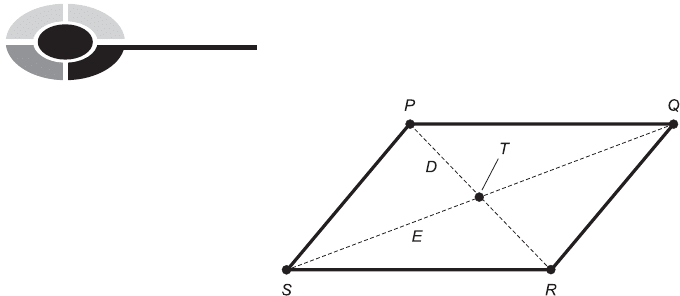
BISECTION OF PARALLELOGRAM DIAGONALS

Suppose we have a parallelogram deﬁned by four distinct points P, Q, R, and

S. Let D be the straight diagonal connecting P and R; let E be the straight

diagonal connecting Q and S (Fig. 9-23). Then D and E bisect each other

at their intersection point T. In addition, the following pairs of triangles

are congruent:

PQT ﬃ RST

QRT ﬃ SPT

The converse of the foregoing is also true: if we have a plane quadrilat-

eral whose diagonals bisect each other, then that quadrilateral is a paralle-

logram.

RECTANGLE

Suppose we have a parallelogram deﬁned by four distinct points P, Q, R, and

S. Suppose any of the following statements is true:

ﬀPQR ¼ 90



ﬀQRS ¼ 90



ﬀRSP ¼ 90



ﬀSPQ ¼ 90



Then all four interior angles measure 908, and the parallelogram is a

rectangle: a four-sided plane polygon whose interior angles are all congruent

(Fig. 9-24). The converse of this is also true: if a quadrilateral is a rectangle,

then any given interior angle has a measure of 908.

Fig. 9-23. The diagonals of a parallelogram bisect each other.

PART 3 Shapes and Places

216

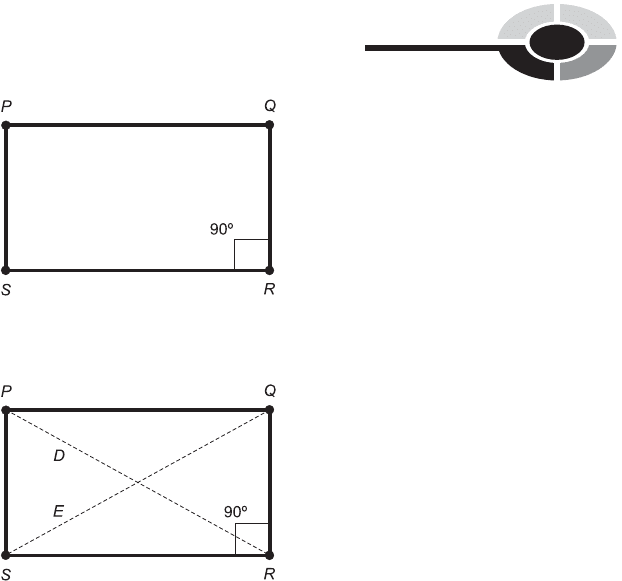
RECTANGLE DIAGONALS

Imagine a parallelogram deﬁned by four distinct points P, Q, R, and S. Let D

be the straight diagonal connecting P and R; let E be the straight diagonal

connecting Q and S. Let the length of D be denoted by d; let the length

of E be denoted by e (Fig. 9-25). If d ¼ e, then the parallelogram is a

rectangle. The converse is also true: if a parallelogram is a rectangle, then

d ¼ e. A parallelogram is a rectangle if and only if its diagonals have equal

lengths.

RHOMBUS DIAGONALS

Imagine a parallelogram deﬁned by four distinct points P, Q, R, and S. Let D

be the straight diagonal connecting P and R; let E be the straight diagonal

connecting Q and S.IfD is perpendicular to E, then the parallelogram is a

rhombus, which is a four-sided plane polygon whose sides are all equally

long (Fig. 9-26). The converse is also true: if a parallelogram is a rhombus,

then D is perpendicular to E. A parallelogram is a rhombus if and only if

its diagonals intersect at a right angle.

Fig. 9-24. If a parallelogram has one right interior angle, then the parallelogram is

a rectangle.

Fig. 9-25. The diagonals of a rectangle have equal length.

CHAPTER 9 Geometry on the Flats 217

TRAPEZOID WITHIN TRIANGLE

Imagine a triangle deﬁned by three distinct points P, Q, and R. Let S be the

midpoint of side PR, and let T be the midpoint of side PQ. Then the straight

line segments ST and RQ are parallel, and the ﬁgure deﬁned by STQR

is a trapezoid: a four-sided plane polygon with one pair of parallel sides

(Fig. 9-27). In addition, the length of line segment ST is half the length of

line segment RQ.

MEDIAN OF A TRAPEZOID

Suppose we have a trapezoid deﬁned by four distinct points P, Q, R, and S.

Let T be the midpoint of side PS, and let U be the midpoint of side QR. Line

segment TU is called the median of trapezoid PQRS. Let M be the polygon

deﬁned by P, Q, U, and T; let N be the polygon deﬁned by T, U, R, and S.

These two polygons, M and N, are trapezoids, as shown in Fig. 9-28.

Fig. 9-26. The diagonals of a rhombus are perpendicular.

Fig. 9-27. A trapezoid within a triangle.

PART 3 Shapes and Places

218

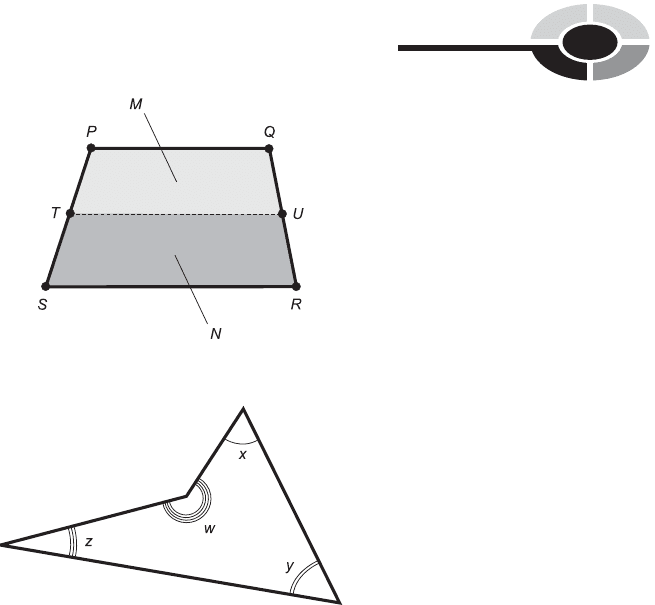
In addition, the length of line segment TU is half the sum of the lengths of

line segments PQ and SR. That is, the length of TU is equal to the average

(arithmetic mean) of the lengths of PQ and SR.

SUM OF INTERIOR ANGLES OF PLANE QUADRILATERAL

Suppose we have a general plane quadrilateral, with no special properties

other than the fact that it is deﬁned by four distinct vertex points that all

lie in the same plane. Let the measures of the interior angles be w, x , y,

and z, as shown in Fig. 9-29. The following equation holds if the angular

measures are given in degrees:

w þ x þ y þ z ¼ 360



PERIMETER OF PARALLELOGRAM

Suppose we have a parallelogram deﬁned by four distinct points P, Q, R, and

S, in which two adjacent sides have lengths d and e as shown in Fig. 9-30.

Fig. 9-28. The median of a trapezoid.

Fig. 9-29. Interior angles of a plane quadrilateral.

CHAPTER 9 Geometry on the Flats 219

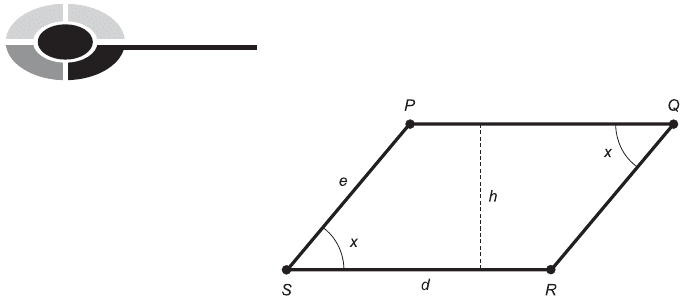
Let d be the base length and let h be the height. Then the perimeter, B ,of

the parallelogram can be found using this formula:

B ¼ 2d þ 2e

INTERIOR AREA OF PARALLELOGRAM

Suppose we have a parallelogram as deﬁned above and in Fig. 9-30.

The interior area, A, of the parallelogram can be found using this formula:

A ¼ dh

PERIMETER OF RHOMBUS

Imagine a rhombus deﬁned by four distinct points P, Q, R, and S. All four

sides of a rhombus have equal lengths. Therefore, the rhombus is a

special case of the parallelogram (Fig. 9-30), in which d ¼ e. Suppose that

the lengths of all four sides are equal to d. The perimeter, B, of this rhombus

is given by the following formula:

B ¼ 4d

INTERIOR AREA OF RHOMBUS

Suppose we have a rhombus as deﬁned above and in Fig. 9-30. The interior

area, A, of the rhombus is given by:

A ¼ dh

Fig. 9-30. Perimeter and area of a parallelogram. If d ¼ e, the ﬁgure is a rhombus.

PART 3 Shapes and Places

220