Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

What is a radian, you ask? Imagine two rays emanating outward from the

center point of a circle. The rays each intersect the circle at a point. Call these

points P and Q. Suppose the distance between P and Q, as measured along

the arc of the circle, is equal to the radius of the circle. Then the measure of

the angle between the rays is one radian (1 rad). There are 2p rad in a full

circle, where p (the lowercase, non-italic Greek letter pi, pronounced ‘‘PIE’’)

stands for the ratio of a circle’s circumference to its diameter. This is a

constant, and it happens to be an irrational number. The value of p is

approximately 3.14159265359, often rounded oﬀ to 3.14159 or 3.14.

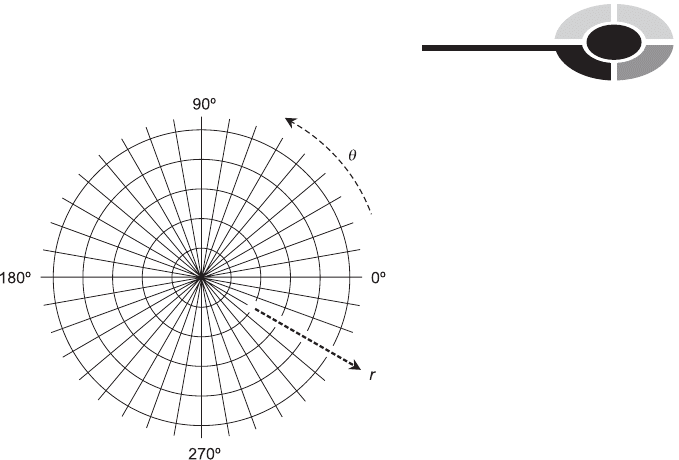
The direction in a polar coordinate system is usually deﬁned counter-

clockwise from a reference axis pointing to the right or ‘‘east.’’ In Fig. 11-7,

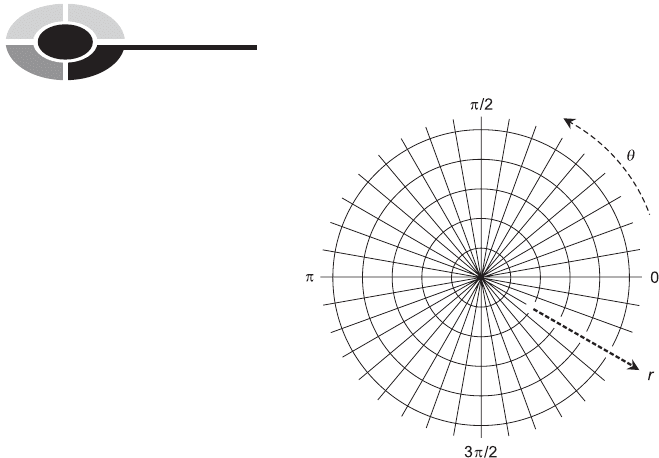
the direction  is in degrees. Figure 11-8 shows the same polar plane, using

radians to express the direction. (The ‘‘rad’’ abbreviation is not used, because

it is obvious from the fact that the angles are multiples of p.) Regardless of

whether degrees or radians are used, the angle on the graph is directly

proportional to the value of .

NEGATIVE RADII

In polar coordinates, it is all right to have a negative radius. If some point is

speciﬁed with r<0, we multiply r by –1 so it becomes positive, and then add

or subtract 1808 (p rad) to or from the direction. That’s like saying, ‘‘Go 3

kilometers (km) southeast’’ instead of ‘‘Go –3 km northwest.’’ Negative

Fig. 11-7. The polar coordinate plane. The angle  is in degrees, and the radius r is in

uniform increments.

CHAPTER 11 Graphing It 261

radii must be allowed in order to graph ﬁgures that represent functions whose

ranges can attain negative values.

NONSTANDARD DIRECTIONS

It’s okay to have nonstandard direction angles in polar coordinates. If the

value of  is 3608 (2p rad) or more, it represents more than one complete

counterclockwise revolution from the 08 (0 rad) reference axis. If the direc-

tion angle is less than 08 (0 rad), it represents clockwise revolution instead

of counterclockwise revolution. Nonstandard direction angles must be

allowed in order to graph ﬁgures that represent functions whose domains

go outside the standard angle range.

PROBLEM 11-4

Provide an example of a graphical object that can be represented as a

function in polar coordinates, but not in Cartesian coordinates.

SOLUTION 11-4

Recall the deﬁnitions of the terms relation and function. When we talk

about a function f, we can say that r ¼ f (). A simple function of  in

polar coordinates is a constant function such as this:

f ðÞ¼3

Fig. 11-8. Another form of the polar coordinate plane. The angle  is in radians, and the

radius r is in uniform increments.

PART 3 Shapes and Places

262

Because f () is just another way of denoting r, the radius, this function tells

us that r ¼ 3. This is a circle with a radius of 3 units.

In Cartesian coordinates, the equation of the circle with radius of 3 units

is more complicated. It looks like this:

þ y

¼ 9

(Note that 9 ¼ 3

, the square of the radius.) If we let y be the dependent

variable and x be the independent variable, we can rearrange the equation

of the circle to get:

y ¼ð9  x

1=2

If we say that y ¼ g(x) where g is a function of x in this case, we are mistaken.

There are values of x (the independent variable) that produce two values of y

(the dependent variable). For example, when x ¼ 0, y ¼3. If we want to say

that g is a relation, that’s ﬁne, but we cannot call it a function.

Some Examples

In order to get a good idea of how the polar coordinate system works, let’s

look at the graphs of some familiar objects. Circles, ellipses, spirals, and

other ﬁgures whose equations are complicated in Cartesian coordinates can

often be expressed simply in polar coordinates. In general, the polar direction

 is expressed in radians. In the examples that follow, the ‘‘rad’’ abbreviation

is eliminated, because it is understood that all angles are in radians.

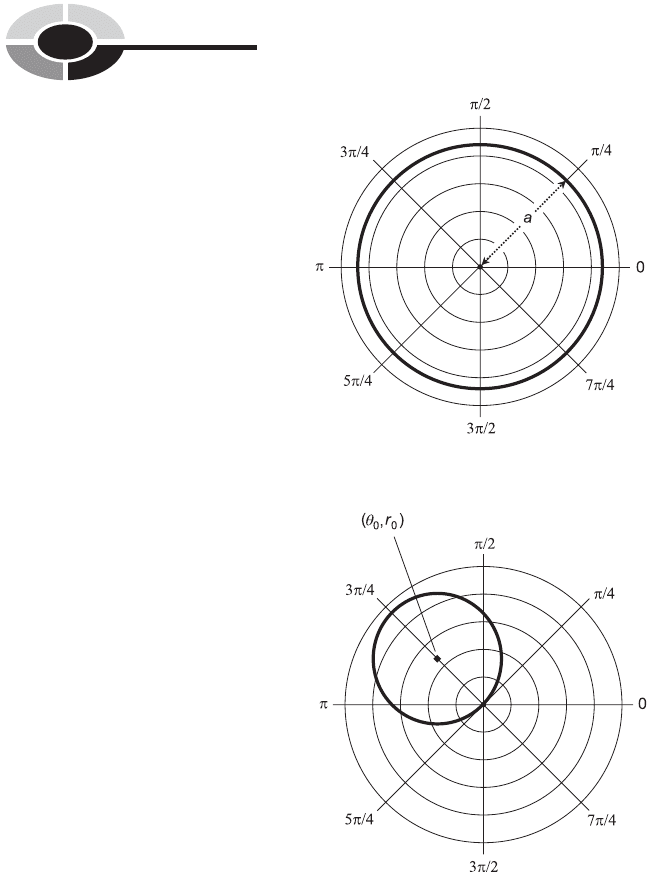
CIRCLE CENTERED AT ORIGIN

The equation of a circle centered at the origin in the polar plane is given

by the following formula:

r ¼ a

where a is a real-number constant greater than 0. This is illustrated in

Fig. 11-9.

CIRCLE PASSING THROUGH ORIGIN

The general form for the equation of a circle passing through the origin and

centered at the point (

, r

) in the polar plane (Fig. 11-10) is as follows:

r ¼ 2r

cos ð  

CHAPTER 11 Graphing It 263

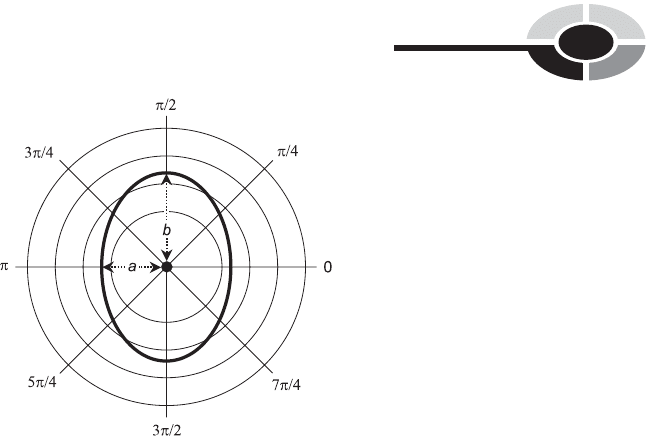
ELLIPSE CENTERED AT ORIGIN

The equation of an ellipse centered at the origin in the polar plane is given by

the following formula:

r ¼ ab=ða

sin

 þ b

cos

Þ

1=2

where a and b are real-number constants greater than 0.

Fig. 11-9. Polar graph of a circle centered at the origin.

Fig. 11-10. Polar graph of a circle passing through the origin.

PART 3 Shapes and Places

264

Here, ‘‘sin’’ represents the sine function and ‘‘cos’’ represents the cosine

function, both of which are available on any good scientiﬁc calculator. The

exponent 2 attached to these functions indicates that after the sine or cosine

has been found, the result should be squared.

In the ellipse, a represents the distance from the origin to the curve as

measured along the ‘‘horizontal’’ ray  ¼ 0, and b represents the distance

from the origin to the curve as measured along the ‘‘vertical’’ ray  ¼ p /2.

This is illustrated in Fig. 11-11. The values a and b represent the lengths of the

semi-axes of the ellipse; the greater value is the length of the major semi-axis,

and the lesser value is the length of the minor semi-axis.

HYPERBOLA CENTERED AT ORIGIN

The general form of the equation of a hyperbola centered at the origin in the

polar plane is given by the following formula:

r ¼ ab=ðb

cos

  a

sin

Þ

1=2

where a and b are real-number constants greater than 0.

Note how similar this is to the equation of the ellipse. But when we look

at Fig. 11-12, which shows a hyperbola, it becomes apparent that the

substitution of the minus sign for the plus sign in this equation makes a big

diﬀerence!

Let D represent a rectangle whose center is at the origin, whose vertical

edges are tangent to the hyperbola, and whose vertices (corners) lie on the

Fig. 11-11. Polar graph of an ellipse centered at the origin.

CHAPTER 11 Graphing It 265

asymptotes of the hyperbola (the long, straight, dashed lines in Fig. 11-12).

Let a represent the distance from the origin to D as measured along the

‘‘horizontal’’ ray  ¼ 0, and let b represent the distance from the origin to D

as measured along the ‘‘vertical’’ ray  ¼ p/2. The values a and b represent

the lengths of the semi-axes of the hyperbola; the greater value is the length of

the major semi-axis, and the lesser value is the length of the minor semi-axis.

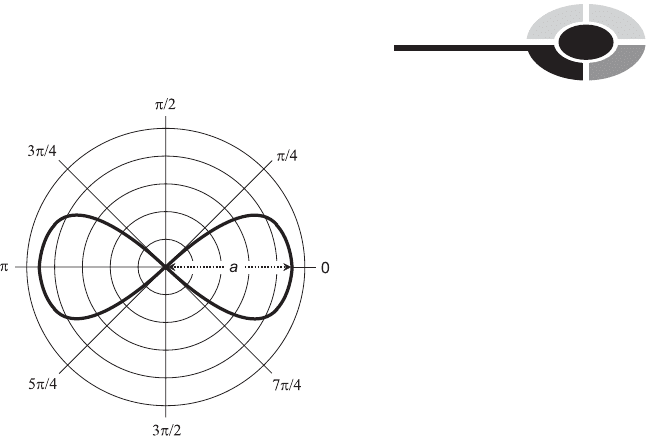
LEMNISCATE

The general form of the equation of a lemniscate centered at the origin in

the polar plane is given by the following formula:

r ¼ aðcos 2Þ

1=2

where a is a real-number constant greater than 0. This is illustrated in

Fig. 11-13.

THREE-LEAFED ROSE

The general form of the equation of a three-leafed rose centered at the origin

in the polar plane is given by either of the following two formulas:

r ¼ a cos 3

r ¼ a sin 3

Fig. 11-12. Polar graph of a hyperbola centered at the origin.

PART 3 Shapes and Places

266

where a is a real-number constant greater than 0. The cosine version

of the curve is illustrated in Fig. 11-14A. The sine version is illustrated in

Fig. 11-14B.

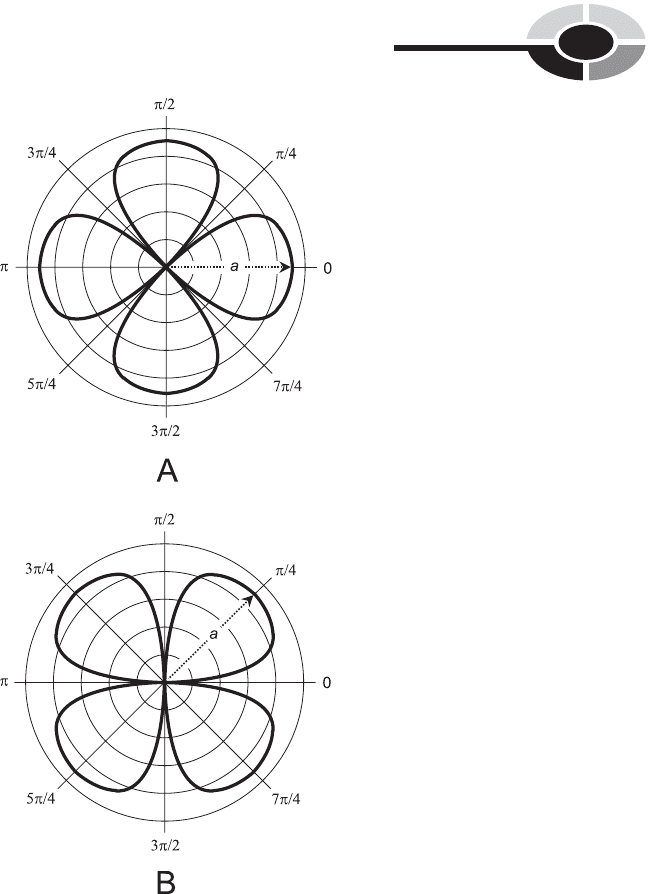
FOUR-LEAFED ROSE

The general form of the equation of a four-leafed rose centered at the origin

in the polar plane is given by either of the following two formulas:

r ¼ a cos 2

r ¼ a sin 2

where a is a real-number constant greater than 0. The cosine version is

illustrated in Fig. 11-15A. The sine version is illustrated in Fig. 11-15B.

SPIRAL

The general form of the equation of a spiral centered at the origin in the polar

plane is given by the following formula:

r ¼ a

where a is a real-number constant greater than 0. An example of this type of

spiral, called the spiral of Archimedes because of the uniform manner in

which its radius increases as the angle increases, is illustrated in Fig. 11-16.

Fig. 11-13. Polar graph of a lemniscate centered at the origin.

CHAPTER 11 Graphing It 267

CARDIOID

The general form of the equation of a cardioid centered at the origin in the

polar plane is given by the following formula:

r ¼ 2að1 þ cos Þ

Fig. 11-14. (A) Polar graph of a three-leafed rose with equation r ¼ a cos 3. (B) Polar graph

of a three-leafed rose with equation r ¼ a sin 3.

PART 3 Shapes and Places

268

where a is a real-number constant greater than 0. An example of this type of

curve is illustrated in Fig. 11-17.

PROBLEM 11-5

What is the value of the constant, a, in the spiral shown in Fig. 11-16?

What is the equation of this spiral? Assume that each radial division

represents 1 unit.

Fig. 11-15. (A) Polar graph of a four-leafed rose with equation r ¼ a cos 2. (B) Polar graph

of a four-leafed rose with equation r ¼ a sin 2.

CHAPTER 11 Graphing It 269

SOLUTION 11-5

Note that if  ¼ p, then r ¼ 2. Therefore, we can solve for a by substituting

this number pair in the general equation for the spiral. We know that

(, r) ¼ (p, 2). Thus 2 ¼ ap. Solving for the constant, a, gives us a ¼ 2/p. The

equation of the spiral is:

r ¼ð2=pÞ

Fig. 11-16. Polar graph of a spiral; illustration for Problem 11-5.

Fig. 11-17. Polar graph of a cardioid; illustration for Problem 11-6.

PART 3 Shapes and Places

270