Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

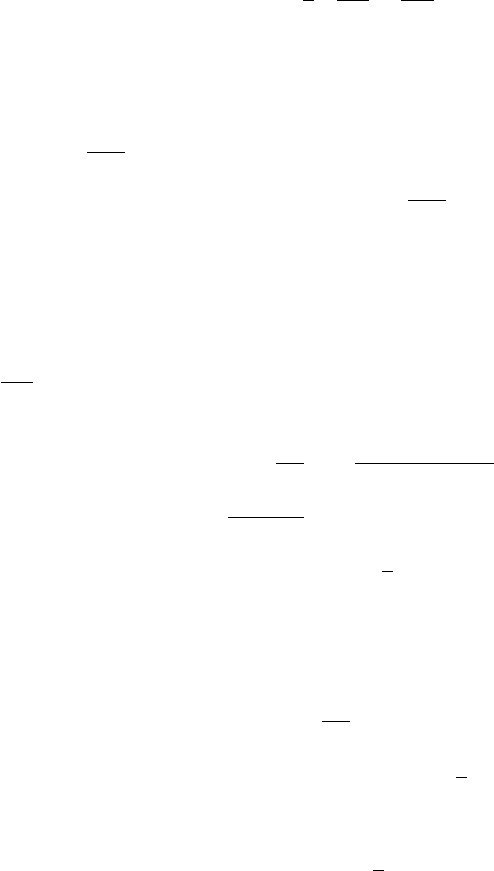
12.2 Elastic rheology 167

For an isotropic body in 3D, the elastic relationship is written in a tensorial form

= λδ

+ 2µε

, (12.2)



∂u

∂x

∂u

∂x



, (12.3)

= ε

+ ε

, (12.4)

where x

and x

are the spatial coordinates (x, y, z), σ

are components of stress,

and u

are components of material displacement vector u = (u

)so

that v

where v

is component of velocity vector v = (v

), ε

are

components of the strain tensor so that ˙ε

Dε

,where˙ε

are components of

strain rate tensor (Chapter 4), ε

is volumetric strain (cubical dilatation)and

λ and µ are two elastic parameters termed Lam

e’s constants (which depend on

pressure temperature and composition). The material displacement characterises

the absolute amount of deformation (i.e. is similar to L in Fig. 12.1), while the

strain tensor ε

reﬂects the relative intensity of this deformation (i.e. is similar to

L

in Fig. 12.1). Formulating pressure through mean normal stress, we can obtain

the following relation

P =−

=−

+ σ

, (12.5)

P =−

3λ + 2µ

(ε

+ ε

) =−Bε

, (12.6)

B = λ +

µ, (12.7)

where B is the bulk modulus (see Chapter 2) also called incompressibility; it estab-

lishes the relation between mean stress (pressure) and volumetric strain. Accord-

ingly, the deviatoric stresses σ



can be formulated as



= σ

−

= σ

+ Pδ

, (12.8)



= σ

− Bε

= 2µ



−



, (12.9)



= 2µε



, (12.10)



= ε

−

, (12.11)

where ε



are components of the deviatoric strain tensor and µ is the shear mod-

ulus or rigidity, which is one of the Lam

e’s constants. The elastic shear modulus

168 Elasticity and plasticity

Fig. 12.3 Force balance for a small triangle ABC used for computing σ

, σ

(a), (b) and σ

, σ

(c), (d) stress components after a clockwise solid body

rotation of the triangle by an angle α around point A.

establishes the relationship between the deviatoric stress and deviatoric strain for

the elastic rheology (µ is thus somewhat similar to the shear viscosity η which

deﬁnes the relationship between the deviatoric stress and the deviatoric strain rate

for a viscous rheology, see Eq. (5.12)).

12.3 Rotation of elastic stresses

An important peculiarity of stress behaviour in a deforming elastic medium consists

in local stress orientation changes due to the rotation of material points. This rotation

is caused by a rigid body rotation which is present in the velocity ﬁeld, which

changes the orientation of principal stress axes for moving Lagrangian points.

Stress rotation changes stress tensor components but not the stress invariants.

The way of computing of various elastic stress components after rotation of a

Lagrangian point by an angle α can be derived on the basis of analysing the force

balance for a small triangle ABC, as shown in Fig. 12.3. Let us take a small triangle

12.3 Rotation of elastic stresses 169

with two sides parallel to the x and y axes oriented as shown in Fig. 12.3(a). The

force equilibrium condition requires that forces acting on the outside of the triangle

balance each other and that the resulting force is zero

= f

+ f

= 0, (12.12)

= f

+ f

= 0, (12.13)

where f are forces acting on different sides of the triangle from the outside. These

forces can be computed from shear and normal stresses as discussed in Chapter 4

(note that arrows shown on side AC correspond to the counter-force part of σ

and

which therefore have a minus sign

cos(α),

sin(α),

= σ



cos(α),

= σ



sin(α),

=−σ

cos(α),

= σ

sin(α),

=−σ



sin(α),

= σ



cos(α),

=−σ

cos(α),

= σ

sin(α),

where

and

are the lengths of the respective triangle sides. Then,

Equations (12.12)and(12.13) can be converted to yield

= σ



cos(α) + σ



sin(α) − σ

cos(α) + σ

sin(α) = 0, (12.14)

=−σ



sin(α) + σ



cos(α) − σ

cos(α) + σ

sin(α) = 0. (12.15)

By multiplying Eq. (12.14)bycos(α)andEq.(12.15)bysin(α), we obtain



cos

(α) + σ



sin(α)cos(α) −σ

cos

(α) + σ

sin(α)cos(α) = 0,

(12.16)

−σ



sin

(α) + σ



cos(α)sin(α) − σ

cos(α)sin(α) + σ

sin

(α) = 0.

(12.17)

By subtracting Eq. (12.17) from Eq. (12.16)weget



(cos

(α) + sin

(α)) −σ

cos

(α) + σ

sin(α)cos(α)

+σ

cos(α)sin(α) −σ

sin

(α) = 0,

170 Elasticity and plasticity

which can be further be simpliﬁed to



= σ

cos

(α) + σ

sin

(α) − σ

sin(2α) (12.18)

by using σ

= σ

and the trigonometric relations sin

(α) + cos

(α) = 1and

2sin(α)cos(α) = sin(2α).

Similarly, by multiplying Eq. (12.14)bysin(α)andEq.(12.15)bycos(α), and

adding them to each other we obtain the following expression for σ



(σ

− σ

)sin(2α) + σ

cos(2α) (12.19)

using the trigonometric relation cos

(α) − sin

(α) = cos(2α) (verify as an exer-

cise).

Obviously, after the triangle has been rotated clockwise by an angle α around

point A (Fig. 12.3b), the AB side becomes parallel to the y-axis and σ



, σ



will

correspond to the respective stress components σ

xx(r)

, σ

yx(r)

for the rotated system.

Similarly, by analysing Fig. (12.3c,d), the following expressions for the corrected

stress components σ



and σ



can be obtained (verify as an exercise))



= σ

sin

(α) + σ

cos

(α) + σ

sin(2α), (12.20)



(σ

− σ

)sin(2α) + σ

cos(2α). (12.21)

Equations (12.19)and(12.21) are obviously equivalent since σ

= σ

. Note that

rotation does not change the ﬁrst stress invariant (mean normal stress, pressure)

and thus



+ σ



= σ

+ σ

=−2P.

Equations for rotating deviatoric normal stresses are similar to (12.18)and(12.20)

since subtracting mean stress does not change the form of these expressions, hence



= σ



cos

(α) + σ



sin

(α) − σ

sin(2α), (12.22)



= σ



sin

(α) + σ



cos

(α) + σ

sin(2α). (12.23)

The condition σ



+ σ



= 0 is also satisﬁed due to σ



+ σ



= 0.

If α is very small and tends to 0, then cos(α) tends to 1, sin

(α) tends to 0, and

sin(α) tends to α. In this case, Equations (12.18)−(12.23) can be simpliﬁed to the

Jaumann co-rotation formulas, which are often used in numerical modelling of

elastic problems to account for effects of solid body rotation of stresses



= σ

− σ

2α, (12.24)



= σ

+ σ

2α, (12.25)



= σ

+ (σ

− σ

)α. (12.26)

12.3 Rotation of elastic stresses 171

In a complex velocity ﬁeld, the intensity of rotation is deﬁned by the local rotation

rate ω which can be computed from the local velocity ﬁeld as

ω =

∂α

∂t



∂v

∂x

−

∂v

∂y



. (12.27)

Note that the expressions for stress rotation and formulation of ω depend on

the convention for normal stresses – if they are taken to be positive (here) or negative

(e.g. Turcotte and Schubert, 2002) under extension,

orientation of x and y axes,

deﬁnition whether clockwise rotation direction is taken to be positive (here) or negative

(e.g. Turcotte and Schubert, 2002).

In particular, Equation (12.27) may become invalid, if the deﬁnitions of stresses,

axes and rotation are different from those used here. In this case, Equations

(12.18)−(12.27) should not be used ‘mechanically’, but should rather be re-derived

on the basis of a similar analysis.

In 3D, the rotation rate is represented by a rotation rate tensor with components

deﬁned as



∂v

∂x

−

∂v

∂x



, when



∂v

∂x

−

∂v

∂x



> 0forclockwise rotation,

(12.28)



∂v

∂x

−

∂v

∂x



, when



∂v

∂x

−

∂v

∂x



> 0forclockwise rotation,

(12.29)

where i and j are coordinate indices; x

and x

are spatial coordinates and the

view at the ij-plane should be taken in the direction of the third axis. In contrast

to symmetric stress and strain rate tensors (i.e. σ

= σ

,˙ε

= ˙ε

), the rotation

rate tensor is anti-symmetric (i.e., ω

=−ω

) and the normal components of this

tensor are always equal to zero (i.e., ω

= ω

= 0). One possible way of

computing both total and deviatoric stress rotation in 3D is to use the general form

of the Jaumann stress rate

total stress:

˙σ

ij(Jaumann)

= σ

− ω

, (12.30a)

deviatoric stress

˙σ



ij(Jaumann)

= σ



− ω



, (12.30b)

where ˙σ

ij(Jaumann)

is the rate of change for the σ

stress component and the repeated

index k indicates a summation. Using Eq. (12.30) in 3D for example, the σ



172 Elasticity and plasticity

deviatoric stress component yields

˙σ



xx(Jaumann)

= σ



+ σ

− ω



− ω

(12.31a)

˙σ



xx(Jaumann)

= σ

+ σ

− ω

, (12.31b)

˙σ



xx(Jaumann)

= 2σ

+ 2σ

, (12.31c)

where ω



∂v

∂x

−

∂v

∂x



= 0, ω



∂v

∂y

−

∂v

∂x



=−ω

and ω



∂v

∂z

−

∂v

∂x



=−ω

, according to Eq. (12.29). Similar derivations can also

be done for other deviatoric stress components (verify these as an exercise)

˙σ



yy(Jaumann)

= 2σ

+ 2σ

, (12.32)

˙σ

zz(Jaumann)

= 2σ

+ 2σ

, (12.33)

˙σ

xy(Jaumann)

= ˙σ

yx(Jaumann)





− σ





+ σ

− ω

, (12.34)

˙σ

xz(Jaumann)

= ˙σ

zx(Jaumann)





− σ





+ σ

− ω

, (12.35)

˙σ

yz(Jaumann)

= ˙σ

zy(Jaumann)





− σ





+ σ

− ω

. (12.36)

It is worth mentioning that in continuum mechanics, apart from the Jaumann stress

rate, typically used in geodynamic modelling, there are a large variety of other

objective stress rate formulations such as the Truesdell rate, the Green–Naghdi

rate, the Oldroyd rate, the convective rate etc. (e.g. Shabana, 2008). However, the

other objective derivatives (beside Jaumann) do not preserve the deviatoric property

of a tensor. Hence, using them in our case is not straightforward as our formulations

assume a splitting of stress into a deviatoric and homogeneous (pressure) part.

12.4 Maxwell visco-elastic rheology

A visco-elastic rheology is obtained by combining viscous (Eq. (5.11)) and elas-

tic (Eq. (12.10)) rheological relations under certain physical assumptions (e.g.

Turcotte and Schubert, 2002, Chapter 7, Sections 7–10). In numerical geodynamic

modelling, the Maxwell visco-elastic rheology is the most commonly used; it is

based on the assumption that both viscous and elastic deformations are happen-

ing under the same applied deviatoric stress σ



such that bulk strain rate ˙ε



can

be represented as a sum of viscous ˙ε



ij(viscous)

and elastic ˙ε



ij(elastic)

strain rates (see

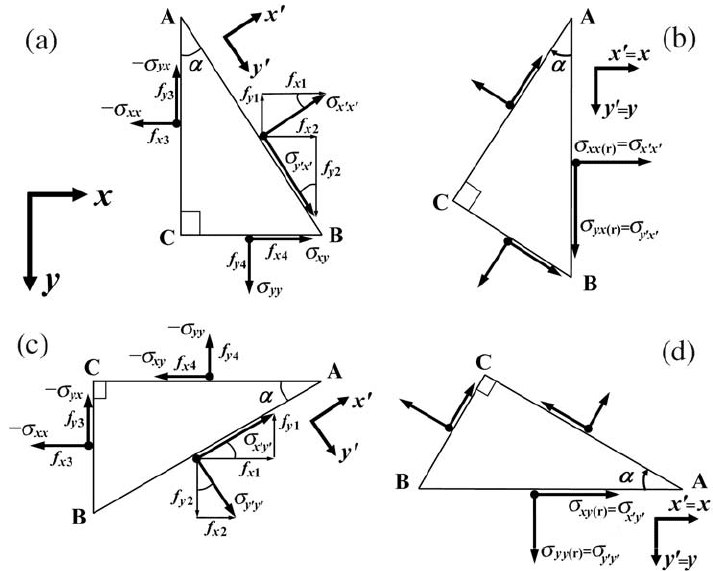
Fig. 12.4 for the relationship between the viscous and elastic deformations of a

Maxwell body)

˙ε



= ˙ε



ij(viscous)

+ ˙ε



ij(elastic)

, (12.37)

12.5 Plastic rheology 173

Fig. 12.4 Schematic representation of the Maxwell visco-elastic rheology. The

solid line shows a typical pattern of visco-elastic stress buildup under the condition

of a linearly growing deformation (dashed line). Deformation initially starts in an

elastic mode (see shortening of the spring) but with the growing stress, viscous

deformation activates and becomes dominant (see movement of the dashpot) and

stress stabilises. The length of the black arrows reﬂects the magnitude of the

applied stress at different moments in time.

which can then be obtained from the rheological relations (5.11) and (12.10) under

the assumption that the term δ

bulk

˙ε

kk(viscous)

in Eq. (5.11) is negligible and the

shear modulus in Eq. (12.10) is constant;

˙ε



ij(viscous)

2η



, (12.38)

˙ε



ij(elastic)

D ε



ij(elastic)

D





2µ



2µ

D σ



, (12.39)

˙ε



2η



2µ

D σ



, (12.40)

where

D σ



is the objective co-rotational time derivative of the deviatoric stress

component σ



which includes effects of stress rotation discussed above.

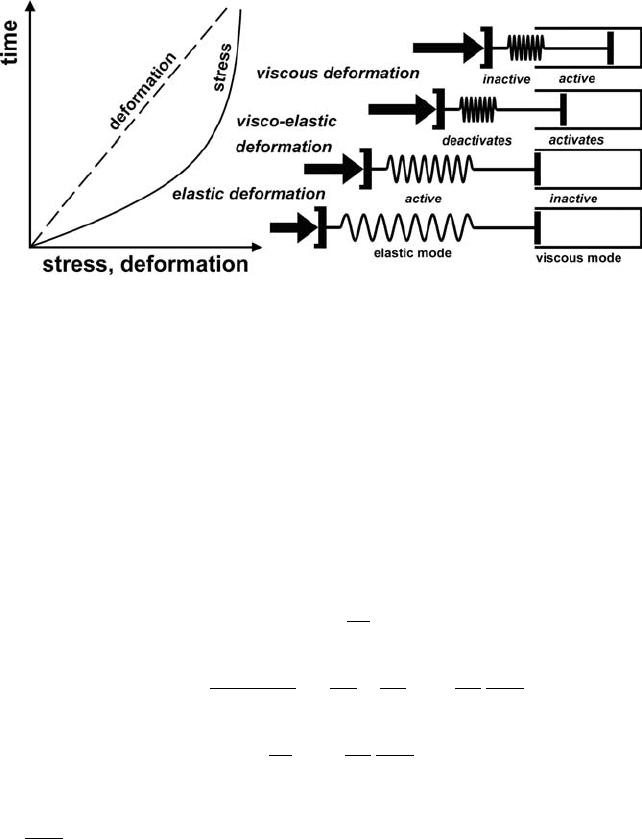
12.5 Plastic rheology

The plastic rheology assumes that an absolute shear stress limit σ

yield

exists for

a body and after reaching this limit plastic yielding occurs (Fig. 12.5). Like vis-

cous deformation, plastic yielding is irreversible, but the pattern of deformation is

notably different (Fig. 12.6): plastic creep is localised and forms multiple highly

deformed shear zones separating relatively undeformed blocks.

174 Elasticity and plasticity

Fig. 12.5 Relationship between the applied stress σ and deformation L,ofan

elastic–plastic body with initial length L. Elastic deformation changes to plastic

yielding after reaching a stress limit σ

yield

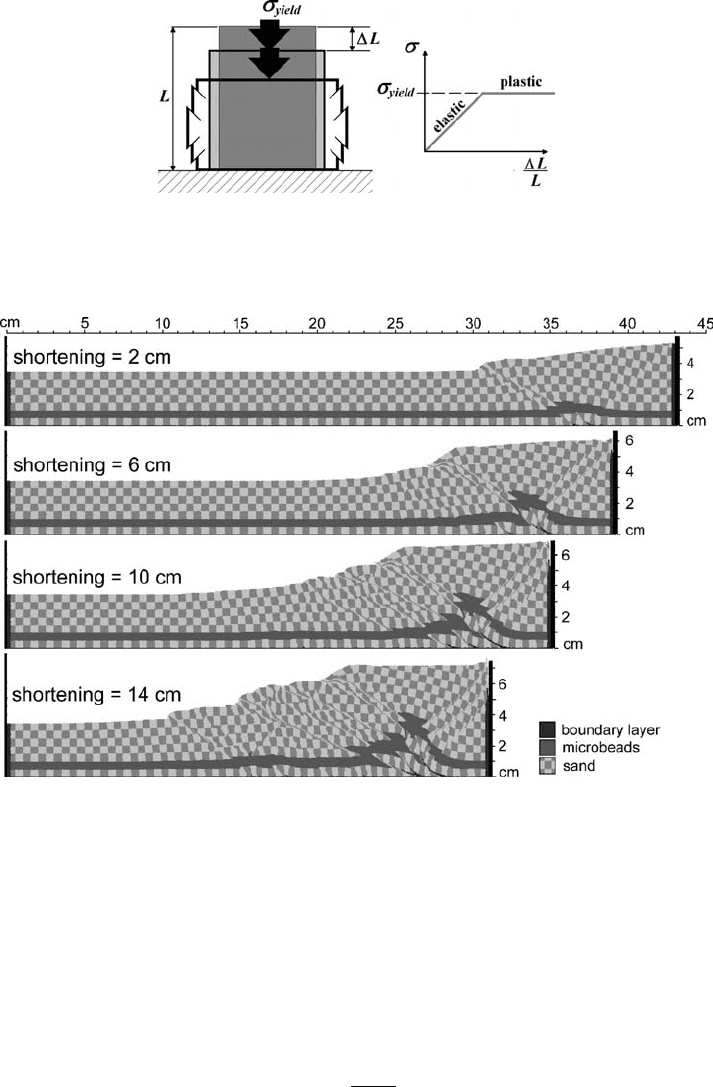
Fig. 12.6 Plastic deformation of sand in a numerical sandbox experiment (Buiter

et al., 2006; Gerya and Yuen, 2007). Irreversible localised plastic deformation

forms multiple, highly deformed shear zones separating relatively undeformed

blocks.

The plastic strength σ

yield

of a rock generally depends on the mean stress of the

solid (P

solid

= P) and on the pore ﬂuid pressure (P

ﬂuid

) such that:

yield

= C +sin(ϕ)P, (12.41)

sin(ϕ) = sin(ϕ

dry

)(1 − λ), (12.42)

λ =

ﬂuid

solid

, (12.43)

12.6 Visco-elasto-plastic rheology 175

where C is the cohesion (residual strength at P =0), φ is the effective internal

friction angle (φ

dry

stands for dry rocks) and λ is the pore ﬂuid pressure factor. For

dry fractured crystalline rocks, sin(φ) is independent of composition and varies from

0.85 at P < 200 MPa to 0.60 at higher pressure (Byerlee law, Byerlee, 1978; Brace

and Kohlstedt, 1980). The plastic strength of dry rocks thus strongly increases with

pressure to a limit of several GPa. The strength is limited by the Peierls mechanism

of plastic deformation (Evans and Goetze, 1979; Kameyama et al., 1999; Karato,

2008).

The Peierls mechanism is a temperature-dependent mode of plastic deforma-

tion (also called exponential creep) which takes over from the dislocation creep

mechanism at elevated stresses (typically above 0.1 GPa). Rheological relation-

ships (ﬂow law) for the Peierls creep are commonly represented as (Katayama and

Karato, 2008)

˙ε

= A

Peierls

exp



−

+ PV



1 −



Peierls







, (12.44)

where ˙ε

and σ

are second invariants of strain rate and stress, respectively and

Peierls

, A

Peierls

, E

and V

are experimentally determined parameters (Chapter 6):

Peierls

is the Peierls stress that limits the strength of the material and is similar to

yield

in Eq. (12.41), A

Peierls

is a material constant for the Peierls creep (Pa

−2

−1

), E

is the activation energy (J/mol), V

is the activation volume (J/Pa/mol). The choice

of the exponents k and q in Eq. (12.44) depends on the shape and geometry of obsta-

cles that limit the dislocation motion. Microscopic models show that k and q should

have the following ranges 0 < k ≤1, 1 ≤q ≤2(Kockset al., 1975). In contrast to

other types of plasticity, Peierls creep is already activated at stresses that are notably

lower than the actual strength of material given by σ

Peierls

. This deformation mech-

anism is very important, in particular for deformation of subducting slabs charac-

terised by lowered temperature and elevated stresses compared to the surrounding

mantle (e.g. Karato et al., 2001), or for lithospheric-scale shear localisation (Kaus

and Podladchikov, 2006).

Further information about various types of plasticity used in geosciences such

as Mohr–Coulomb, Von-Mises, Drucker–Prager and Treska models can be found

in the books of Turcotte and Schubert (2002) and Ranalli (1995).

12.6 Visco-elasto-plastic rheology

In nature, the general behaviour of rocks is altogether visco-elasto-plastic, which

can be formulated by decomposing the total deviatoric strain rate ˙ε



into the three

176 Elasticity and plasticity

respective components:

˙ε



= ˙ε



ij (viscous)

+ ˙ε



ij (elastic)

+ ˙ε



ij (plastic)

, (12.45)

where

˙ε



ij(viscous)

2η



(under condition of negligible δ

bulk

˙ε

kk(viscous)

in Eq. (5.11)),

(12.46)

˙ε



ij(elastic)

2µ

D σ



, (12.47)

˙ε



ij(plastic)

= 0forσ

<σ

yield

, ˙ε



ij (plastic)

= χ

∂G

plastic

∂σ



= χ



2σ

for σ

= σ

yield

(12.48)

plastic

= σ

, (12.49)



2

, (12.50)

where

D σ



is the objective co-rotational time derivative of the deviatoric stress

component σ



, equation (12.48)istheplastic ﬂow rule, σ

yield

is the plastic yield

strength for a given rock, G

plastic

is the plastic ﬂow potential, which reﬂects the

amount of mechanical energy per unit volume that supports plastic deformation,

Pa =

; σ

is the second deviatoric stress invariant and χ is the plastic

multiplier, which satisﬁes the plastic yielding condition

= σ

yield

. (12.51)

The plastic multiplier is a variable scaling coefﬁcient which connects, in a uniform

way, components of the plastic strain rate ˙ε



ij (plastic)

with the local stress distribu-

tion in places where the yielding condition (12.51) is reached. This coefﬁcient is

unknown a priori and should be determined locally at each moment of time by

solving Equations (12.45)−(12.51), based on local values of stresses σ



,strain

rates ˙ε



, viscosity η and shear modulus µ.

This plastic ﬂow rule formulation (Eq. (12.48)) includes deviatoric stress and

strain rate components only and, consequently, the plastic potential formulation

(Eq. (12.49)) is the same for both dilatant (i.e. increasing volume during plas-

tic deformation) and non-dilatant materials. For plastic deformation of dilatant

materials, this formulation is, therefore, combined with the equation describing