Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

11.2 Thermomechanical code structure 157

and

∂P

∂y

from ρg

and ρg

values

≈ Tαρ(g

+ g

We use a standard procedure (Fig. 10.5, Eq. (10.9)) for the formulation of a FD

scheme in order to represent the temperature equation (11.7) in a conservative form

as follows

i,j

Pi,j





i,j

=−



∂q

∂x



i,j

−



∂q

∂y



i,j

+ H

r(i,j )

a(i,j)

s(i,j)

L(i,j)

(11.8)

or in FD formulation

(i,j)

Pi,j

t+t

i,j

− T

i,j

t

=−2

x(i,j+1/2)

− q

x(i,j−1/2)

j+1

− x

j−1

− 2

y(i+1/2,j )

− q

y(i−1/2,j )

i+1

− y

i−1

r(i,j )

+ H

a(i,j)

+ H

s(i,j)

+ H

L(i,j)

or, by grouping the known parameters on the right-hand side

i,j

Pi,j

t

t+t

i,j

+ 2

x(i,j+1/2)

− q

x(i,j−1/2)

j+1

− x

j−1

+ 2

y(i+1/2,j )

− q

y(i−1/2,j )

i+1

− y

i−1

i,j

Pi,j

t

i,j

+ H

r(i,j )

+ H

a(i,j)

+ H

s(i,j)

+ H

L(i,j)

where

x(i,j−1/2)

=−

i,j−1

+ k

i,j

)

t+t

i,j

− T

t+t

i,j−1

− x

j−1

x(i,j+1/2)

=−

i,j

+ k

i,j+1

)

t+t

i,j+1

− T

t+t

i,j

j+1

− x

y(i−1/2,j )

=−

i−1,j

+ k

i,j

)

t+t

i,j

− T

t+t

i−1,j

− y

i−1

y(i+1/2,j )

=−

i,j

+ k

i+1,j

)

t+t

i+1,j

− T

t+t

i,j

i+1

− y

a(i,j)

= T

i,j



x(i−1/2,j )

+ v

x(i+1/2,j )

y(i,j−1/2)

+ v

y(i,j+1/2)



s(i,j)



xx(i−1/2,j −1/2)

˙ε

xx(i−1/2,j −1/2)



xx(i−1/2,j +1/2)

˙ε

xx(i−1/2,j +1/2)



xx(i+1/2,j −1/2)

˙ε

xx(i+1/2,j −1/2)



xx(i+1/2,j +1/2)

˙ε

xx(i+1/2,j +1/2)

+2σ

xy(i,j)

˙ε

xy(i,j)

158 2D thermomechanical code structure

where the index t + t denotes values for the next time instant to be reached

by the time-stepping procedure and t is the optimal time step (see Step 5 of

the algorithm); H

r(i,j )

, H

a(i,j)

, H

s(i,j)

, α

i,j

, ρ

i,j

, C

Pi,j

, σ

xy(

i,j

)

,˙ε

xy(i,j)

, v

x(i−1/2,j )

etc. are values of the corresponding parameters for various nodes of the staggered

grid ((Fig. 11.2): scalar properties are interpolated from the markers using relation

(8.18) (Fig. 8.8), vectors and tensors are taken from the corresponding surrounding

nodes.

To solve the temperature equation, we invert directly the global matrix with

a direct method. The matrix also contains the linear equations associated with

the thermal boundary conditions. The overall numbering of T

t+t

i,j

for the global

temperature matrix that deﬁnes the order of processing of temperature equations

(11.8) is given in Exercise 10.1 (Eq. 10.24).

For advection of temperature, we use the same marker-in-cell technique

(Chapter 10) as is commonly used for advection of material ﬁeld properties, such as

the density, viscosity, chemical composition etc. The interpolation of the calculated

temperature changes from the Eulerian nodal points to the moving markers reduces

numerical diffusion in an efﬁcient manner (Chapter 10), which represents one of

the highlights of our computational strategy. This method does not produce any

smoothing of the temperature distribution between adjacent markers (Fig. 11.2,dia-

gram for step 7), thus resolving the thermal structure of a numerical model in much

ﬁner details. Non-physical small-scale (subgrid) temperature oscillations appear-

ing on markers (Fig. 10.7(a)) in the case of strong chaotic mixing are removed

(Fig. 10.7(b)) by using a consistent subgrid diffusion operation (Eqs. (10.15)–

(10.19)).

11.3 Adding self-gravity and free surface

For the case when one wants to model the dynamics of self-gravitating planetary

bodies, the numerical algorithms presented so far can be easily modiﬁed to take

a variable gravity ﬁeld and a free planetary surface into account. This is done by

solving the Poisson equation for gravity potential after computing the nodal density

ﬁeld from markers, and before solving the momentum and continuity equations

(Fig. 11.3). A staggered grid corresponding to this new algorithm is shown in

Fig. 11.4.

In this grid, the gravitational potential  (Chapter 2) is deﬁned at the cell centres

(i.e. at the pressure nodes) and computed according to the 2D Poisson equation

∂



∂x

∂



∂y

= 4KπGρ, (11.16)

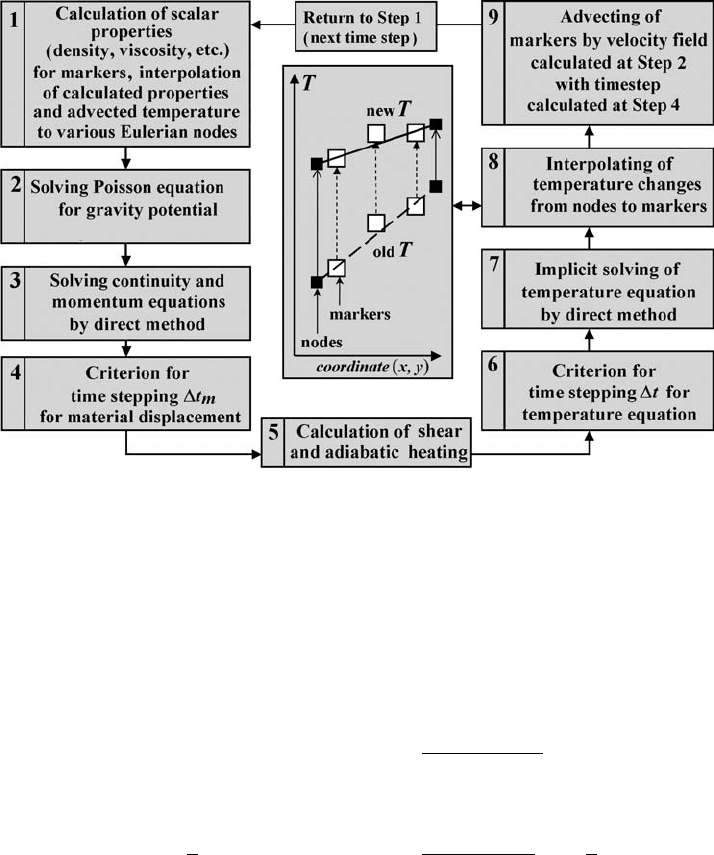
11.3 Adding self-gravity and free surface 159

Fig. 11.3 Flow chart representing the modiﬁed algorithm of the numerical thermo-

mechanical viscous 2D code allowing the modelling of self-gravitating planetary

bodies with a fully staggered Cartesian grid (Gerya and Yuen, 2007). Note the

new Step 2 compared to Fig. 11.1.

where G is the gravitational constant and K depends on the geometry of self-

gravitating body modelled in 2D (K =1andK =2/3 stand for cylindrical and

spherical geometry, respectively). The factor K =2/3 scales the 2D gravity ﬁeld

inside a cylinder of constant density ρ

(r)

cylindrical

= πGρr

,g(r)

cylindrical

=−

∂(r)

cylindrical

∂r

=−2πGρr,

to a 3D gravity ﬁeld inside a sphere of the same density

(r)

spherical

πGρr

,g(r)

spherical

=−

∂(r)

spherical

∂r

=−

πGρr,

where r is the distance from the centre of the cylinder/sphere. It should be men-

tioned that this simpliﬁed scaling does not allow the exact reproduction of a spher-

ical gravity ﬁeld in 2D. In particular, the gravitational acceleration is noticeably

overestimated outside the self-gravitating body since it is proportional to 1/r for a

cylindrical gravity ﬁeld and to 1/r

for a spherical one. Our scaling approach allows

us to capture changes in an internal gravity ﬁeld that acts on a self-gravitating body

with a changing internal mass distribution (Lin et al., 2009). In many cases this is

sufﬁcient for the purposes of modelling internal planetary processes.

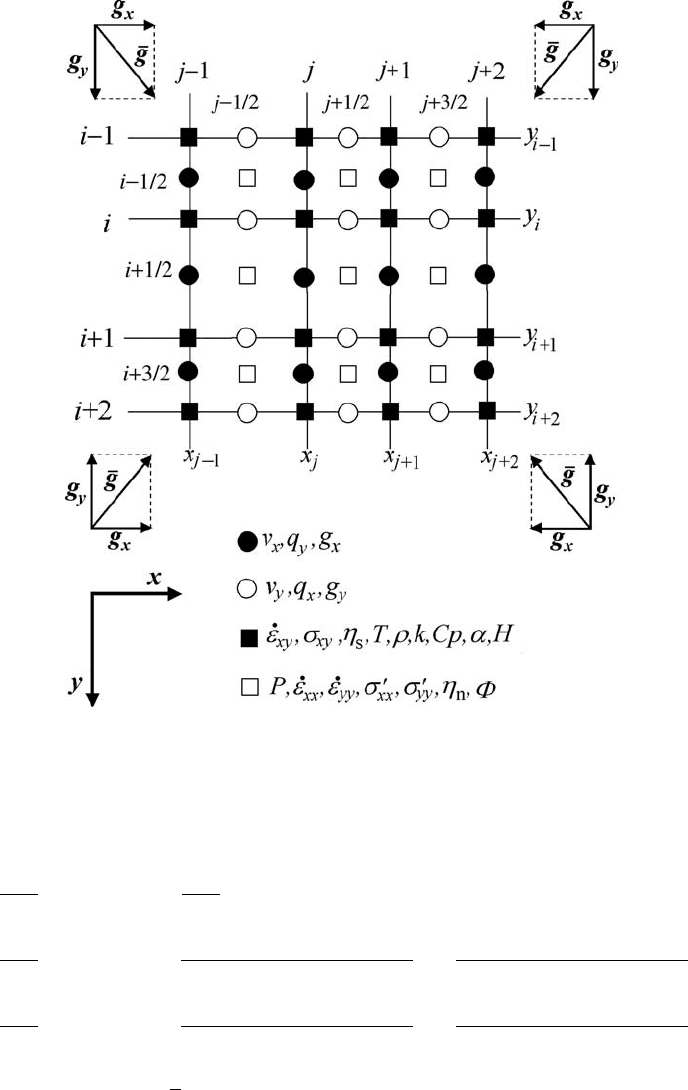
160 2D thermomechanical code structure

Fig. 11.4 Staggered 2D irregularly spaced numerical grid which corresponds to

the algorithm presented in Fig. 11.3.

Discretising Eq. (11.16) in 2D is rather simple and uses a 5-node stencil typical

for approximating the Poisson equation with ﬁnite differences



∂



∂x



i+1/2,j +1/2



∂



∂x



i+1/2,j +1/2

= 4KπGρ

i+1/2,j +1/2

, (11.17)



∂



∂x



i+1/2,j +1/2

= 2



i+1/2,j +3/2

−

i+1/2,j +1/2

j+2

− x

)(x

j+1

− x

)

− 2



i+1/2,j +1/2

−

i+1/2,j −1/2

j+1

− x

j−1

)(x

j+1

− x

)



∂



∂y



i+1/2,j +1/2

= 2



i+3/2,j +1/2

−

i+1/2,j +1/2

(

i+2

− y

)(

i+1

− y

)

− 2



i+1/2,j +1/2

−

i−1/2,j +1/2

(

i+1

− y

i−1

)(

i+1

− y

)

i+1/2,j +1/2

(ρ

i,j

+ ρ

i,j+1

+ ρ

i+1,j

+ ρ

i+1,j +1

11.3 Adding self-gravity and free surface 161

where the i, i +1/2andj, j +1/2 indices denote, respectively, the horizontal

and vertical position of the nodal points corresponding to the different physical

parameters (Fig. 11.4) within the staggered grid. We invert the global matrix by

a direct method for solving Poisson Eqs. (11.17), combined with linear equations

for the boundary conditions. The overall numbering of unknowns for the global

gravity potential matrix is given in Exercise 3.2 (Eq. 3.22).

The gravitational acceleration vector components are then deﬁned at respective

Eulerian nodes (see solid and open circles in Fig. 11.4) by numerical differentiation

x (i+1/2,j)

=−2



i+1/2,j +1/2

− 

i+1/2,j −1/2

j+1

− x

j−1

, (11.18)

y (i,j +1/2)

=−2



i+1/2,j +1/2

− 

i−1/2,j +1/2

i+1

− y

i−1

. (11.19)

The new, locally deﬁned gravity acceleration components g

x(i+1/2, j)

and g

y(i, j+1/2)

are then included in the right-hand side of the x-andy-Stokes equations (11.4)and

(11.5) instead of the globally deﬁned values g

and g

, respectively.

Numerical modelling of deformation of a self-gravitating planetary body

requires computing the gravity ﬁeld which changes with time in response to vari-

ations in mass distribution inside the planet. Changes in shape of the planet and

the related planetary surface deformation should also be considered. In order to

tackle these requirements, one can use a ‘spherical-Cartesian’ approach (Honda

et al., 1993; Gerya and Yuen, 2007;Linet al., 2009) that allows the computation of

self-gravitating bodies of arbitrary form on Cartesian grids including the presence

of a free surface:

(1) The body is surrounded by the weak medium (e.g. Fig. 11.5) of very low density

(≤ 1 kg/m

) and low viscosity allowing for a high (10

–10

) viscosity contrast at the

planetary surface.

(2) The gravity ﬁeld is computed by solving the Poisson equation for the gravitational

potential (Eq. (11.17)) associated with the mass (density) distribution portrayed by the

markers at each time step.

(3) While solving the momentum equation, the components of the gravitational accel-

eration vector are computed locally by numerical differentiation of the gravitational

potential (Eqs. (11.18), (11.19)) at the corresponding nodal points.

As seen in Fig. 11.5, the spontaneously formed planetary surface is numeri-

cally stable under conditions of very strong internal deformation inside the planet.

In addition, a spontaneously forming spherical/cylindrical shape of the body is

characteristic for a stable density distribution (i.e. when density increases toward

the core of the body, see ﬁnal stages of Fig. 11.5). No evidence for non-spherical

Cartesian grid dependence of this stable shape was discerned (Lin et al., 2009).

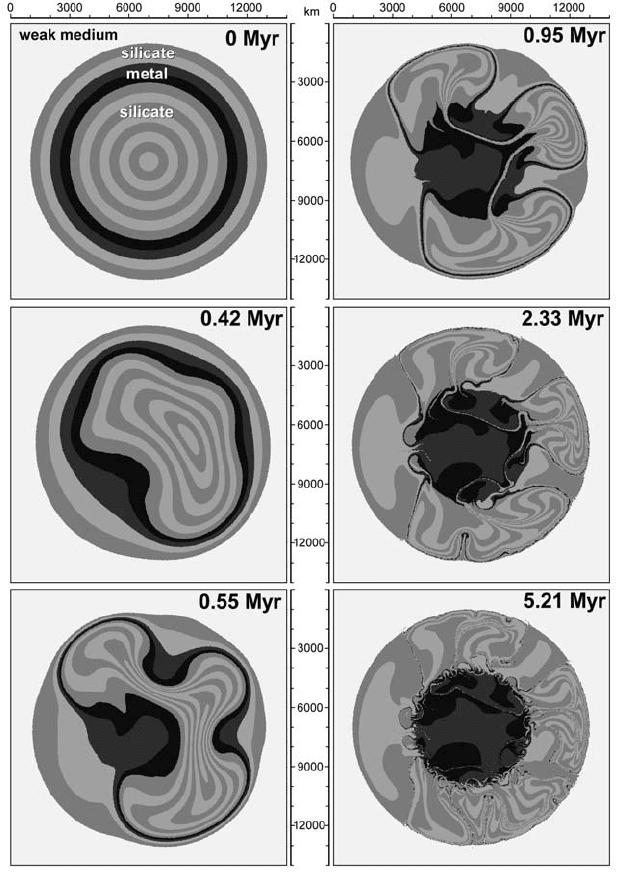
162 2D thermomechanical code structure

Fig. 11.5 Numerical modelling of a self-gravitating planetary body with the use

of spherical-Cartesian method (Gerya and Yuen, 2007).

Using a weak top layer approach for modelling free surfaces is also applica-

ble for normal Cartesian simulations in a prescribed (e.g. purely vertical) gravity

ﬁeld (Schmeling et al., 2008). Combined with various erosion/sedimentation func-

tions, this approach also allows modelling the topography evolution in response to

geodynamic processes with the use of the standard thermomechanical algorithm

(Fig. 11.1). This point will be argued in Chapter 17.

Programming exercise and homework 163

Programming exercise and homework

Exercise 11.1

Program a thermomechanical code (Fig. 11.1) based on a regularly spaced staggered

grid for the case of variable viscosity and thermal conductivity. Combine the

thermal and mechanical solutions programmed for Exercise 10.4 and Exercise 8.5,

respectively. Use the same vertically layered cross-section and prescribe a different

temperature and thermal conductivity for the left (T =1000 K, k =1 W/m/K) and

right (T =1300 K, k =10 W/m/K) layer. Use insulating boundary conditions on all

boundaries. Include radiogenic (10

−6

W/m

and 10

−7

W/m

for the left and right

layer respectively), shear and adiabatic heating terms (Eq. (11.8)) in the temperature

equation (they were already programmed for Exercises 9.3 and 9.4). Restrict the

time step by limiting the maximal temperature changes to 20 K per time step.

If these changes are bigger, then reduce the time step proportionally and repeat

the solution for the second time (temperature equation solving is computationally

inexpensive compared to the momentum and continuity equations). An example is

in i2vis.m.

Elasticity and plasticity

Theory: Elastic rheology. Maxwell visco-elastic rheology. Rotation of

stresses during advection. Plastic rheology. Plastic yielding criterion.

Plastic ﬂow potential. Plastic ﬂow rule.

Exercises: Stress build-up/relaxation with a visco-elastic Maxwell

rheology.

12.1 Why care about elasticity and plasticity?

As mentioned in the Introduction, rocks behave elastically on a relatively short time

scale (<10

years) and, therefore, modelling of relatively fast processes within the

Earth’s crust and mantle (e.g. magma intrusion) should take into account the elas-

tic properties of rocks. On the other hand, rocks at cold temperatures can also be

subjected to localised brittle (at low pressure) and plastic (at higher pressure) defor-

mation, which leads to shear zones and fracture zones in natural rock complexes.

Therefore, if we want to account for this broad range of geodynamic conditions

in our models, we should generally consider the visco-elasto-plastic rheology of

rocks and be able to model such a complex rheology with our thermomechanical

numerical codes. This chapter discusses elastic and plastic rheological behaviours

and compares them to the viscous rheology.

12.2 Elastic rheology

The elastic rheology assumes proportionality of stress and strain (Fig. 12.1). This

is expressed by the Hooke’s law

σ = Eγ, (12.1)

165

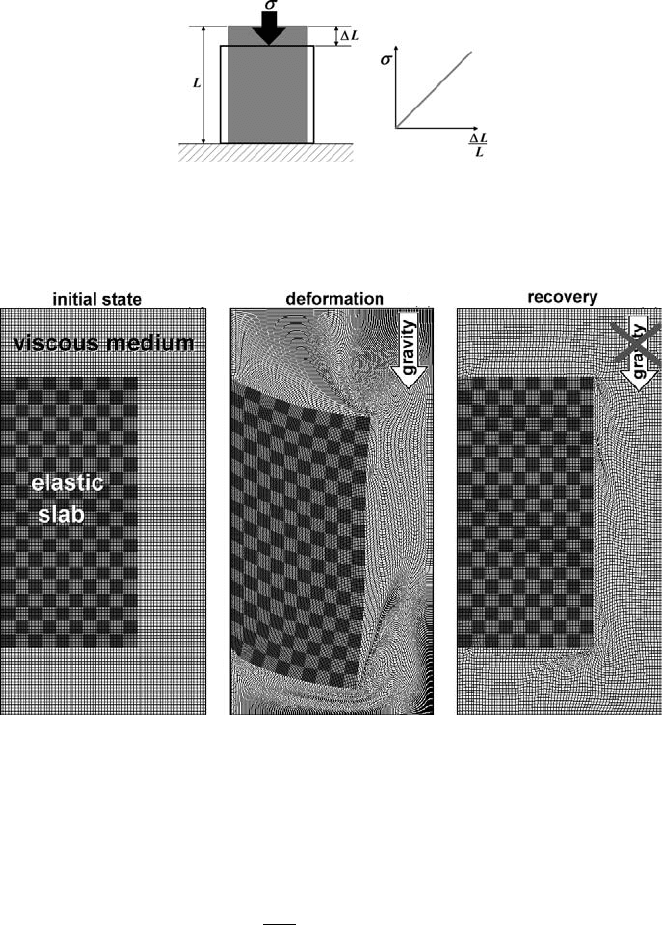
166 Elasticity and plasticity

Fig. 12.1 Relationship between applied stress σ and deformation L, of an elastic

body with initial length L.

(a)

(b)

(c)

Fig. 12.2 Reversible deformation of initially unstressed (a) elastic slab surrounded

by a weak viscous medium (Gerya and Yuen, 2007). Deformation of the slab in (b)

is caused by a vertical gravity ﬁeld. When gravity is ‘removed’, the deformed slab

recovers its original shape (c) while the surrounding medium remains deformed

since viscous deformation is irreversible.

where σ is applied stress, γ =

L

is elastic strain (i.e. displacement L nor-

malised to the initial length L of the deforming body) and E is the proportionality

(elasticity) coefﬁcient. In contrast to viscous deformation, the elastic deformation

is reversible: if the load applied on an elastic body is removed, the body instantly

recovers its original state (Fig. 12.2). This shape recovery effect is reproduced with

a spring.