Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

9.3 Heat generation and consumption 127

in Eq. (9.7b) can be replaced by derivatives and we obtain the Lagrangian heat

conservation equation

ρC

=−

∂q

∂x

−

∂q

∂y

−

∂q

∂z

+ H.

9.3 Heat generation and consumption

There are several types of heat generation/consumption processes that should be

taken into account in the temperature equation

ρC

=−

∂q

∂x

+ H

, (9.8)

where i is a coordinate index, x

is a spatial coordinate and H

, H

and H

are

the radioactive, shear, adiabatic and latent heat productions (W/m

), respectively.

The radioactive heat production (H

) is due to the decay of radioactive

elements that are present in rocks. The amount of radioactive heat production

depends strongly on the type of rocks and typical, easy-to-remember values are:

2 × 10

−6

W/m

for granites, 2 × 10

−7

W/m

for basalts and 2 × 10

−8

W/m

for

mantle rocks (Turcotte and Schubert, 2002).

The shear heat production (H

) is related to dissipation of the mechanical energy

during irreversible non-elastic (e.g., viscous) deformation and can be calculated

via the deviatoric stresses and strain rates as follows

= σ



˙ε



(9.9a)

where i and j are coordinate indices (x, y, z) and the repeated ij indices denotes

summation. In the case of 3D viscous deformation of an incompressible ﬂuid Eq.

(9.9a) becomes

= σ



˙ε

+ σ



˙ε

+ σ



˙ε

+ 2(σ

˙ε

+ σ

˙ε

+ σ

˙ε

). (9.9b)

The adiabatic heat production/consumption (adiabatic heating/cooling) is related

to changes in pressure and can be calculated via pressure changes as follows

= Tα

, (9.10)

where

is the substantive time derivative of pressure. In contrast to shear

and radioactive heating, adiabatic effects can be either positive or negative. It is

known from thermodynamics that the temperature of a substance under conditions

of no thermal exchange increases with increasing pressure and decreases with

decreasing pressure, which thus directly reﬂects the sign of

. The effects of

128 The heat conservation equation

adiabatic heating can be very signiﬁcant in cases of strong changes in pressure, a

fact which has implications for mantle convection.

The latent heat production/consumption (H

) is due to the phase transformations

in rocks subjected to changes in pressure and temperature. A very common type of

latent heat is the latent heat of melting, which is negative (heat sink, H

< 0) for

melting and positive (heat production, H

> 0) for crystallisation.

9.4 Simpliﬁed temperature equations

In a complete form, the temperature equation looks quite complicated, but at least

it does not ‘hide’ three equations in one in contrast to the momentum equation.

In the case of constant thermal conductivity k =const, the temperature equation

simpliﬁes to

ρC

= k

∂

∂x

+ k

∂

∂y

+ k

∂

∂z

+ H

(9.11a)

or,

ρC

= kT + H

+ H

. (9.11b)

When the internal heat production is negligible and there is no advection of

material (purely conductive heat transport), the temperature equation takes a form

which is similar to the Poisson equation

∂T

∂t

= κT, (9.12)

where κ =

ρC

is thermal diffusivity (m

/sec).

If temperature does not change with time, heat conservation is described by a

steady-state temperature equation. The steady-state, Eulerian temperature equation

∂T

∂t

= 0, corresponds to the case when temperature remains constant at immobile,

Eulerian observation points, while the temperature at Lagrangian points can change.

In this case, the temperature equation is as follows,

ρC

(

¯v ·grad(T )

)

=−

∂q

∂x

+ H

, (9.13)

where i is a coordinate index and x

is a spatial coordinate. This form of the

equation is frequently used for computing equilibrium temperature proﬁles across

9.5 Heat diffusion timescales 129

a deforming medium, for example in the case of steady magma ﬂow in a channel.

The steady-state Lagrangian temperature equation

= 0 corresponds to the

case when the temperature does not change at Lagrangian points but can vary at

Eulerian observation points according to the purely advective heat transport,

∂T

∂t

+ ¯v · grad(T ) = 0. (9.14)

In this case, the temperature equation is as follows

−

∂q

∂x

+ H

= 0. (9.15)

The steady-state Eulerian–Lagrangian temperature equation (

∂T

∂t

= 0and

0) holds for the case when no displacement of the medium occurs, pressure and

temperature are constant and therefore H

= 0, H

= 0andH

= 0. This equation

has the simple form

−

∂q

∂x

+ H

= 0, (9.16)

and is often used for the calculation of steady-state geotherms that characterise

changes of temperature with depth in a layered sequence of rocks with variable

radioactive heat production.

Simpliﬁed steady-state temperature equations are often used for obtaining

analytical solutions which are used for testing accuracy of numerical codes

(Chapter 16). Indeed some analytical solutions also exist for more complicated

non steady-state (transient) cases (e.g. Tikhonov and Samarsky, 1972; Shukla,

2005) which will be further discussed in Chapter 16.

9.5 Heat diffusion timescales

One important aspect that can be analysed analytically concerns the timescales of

heat diffusion processes. Heat generated within any region is spread by conduction

(i.e. diffused) on a characteristic timescale (t

diff

) that depends on the width L,of

the region according to

diff

. (9.17)

Therefore, the duration of heat dissipation via conduction grows as the square of

the width (L) of the region. For instance, although the shear heat produced within a

130 The heat conservation equation

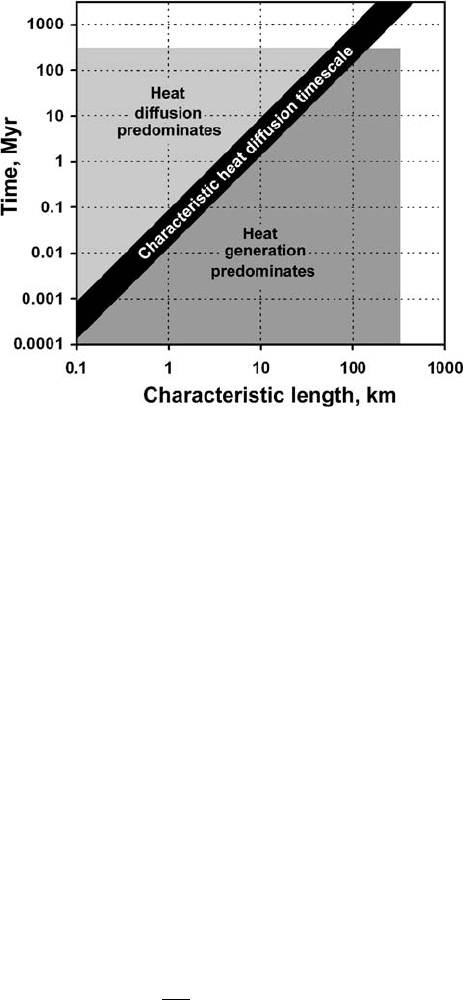
Fig. 9.2 Timescales for different thermal regimes calculated according to the equa-

tion t

diff

= L

/κ with κ =10

−6

/s. Shaded areas show length and timescales

characteristic of collisional orogens (Burg and Gerya, 2005).

100 metre wide shear zone dissipates in only ∼1000 yr, the heat generated within a

1 km wide shear zone requires about 100 000 yr for the similar degree of conductive

cooling (Fig. 9.2).

Analytical exercises

Exercise 9.1

Integrate Equation (9.16) in order to calculate the steady-state temperature proﬁle

across the continental crust with radioactive heat production H

=1 × 10

−6

W/m

if the temperature at the surface is 300 K and temperature at the bottom of the crust

is 700 K. Take the thermal conductivity of the crust to be k = 2W/(mK).

Exercise 9.2

Compute from Eq. (9.13) the steady-state Eulerian temperature proﬁle across the

magmatic channel described in Exercise 5.1 (Fig. 5.2). Assume the temperature

at the channel walls, as well as the temperature gradient along the channel to be

constant. Use T

= 1300 K and

∂T

∂y

= 1 K/m for the analysed horizontal section

across the channel. Take the thermal conductivity to be k = 2 W/(m K) and the

isobaric heat capacity as C

= 1000 J/(kg K).

Programming exercises and homework 131

j+1

(a)

(b)

x(i, j)

xy(i,j)

y(i, j)

s(i, j)

n(i, j)

i+1

xy(i,j)

•

xx(i,j)

•

xx(i,j)

′

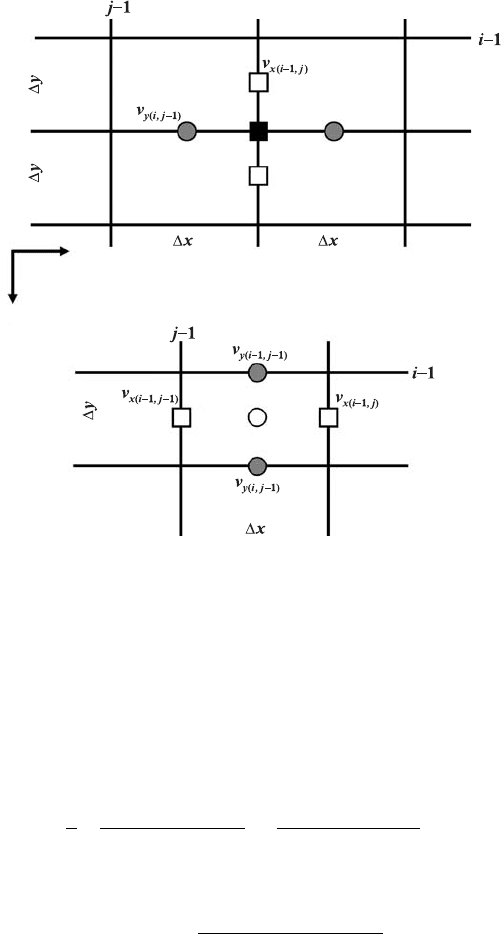
Fig. 9.3 Stencils used for the discretisation of the shear (a) and normal (b) strain

rates and the deviatoric stress components. Indexing of gridlines corresponds to

the basic (density) nodal points. Indexing of different unknowns is made according

to Fig. 7.15.

Programming exercises and homework

Exercise 9.3

Use the variable viscosity model (Exercise 7.2) to compute the strain rate compo-

nents and deviatoric stress components as follows (Fig. 9.3)

˙ε

xy(i,j)



x(i,j)

− v

x(i−1,j )

y

y(i,j)

− v

y(i,j−1)

x



, (9.18)

xy(i,j)

= 2η

s(i,j)

˙ε

xy(i,j)

, (9.19)

˙ε

xx(i,j)

x(i−1,j )

− v

x(i−1,j −1)

x

, (9.20)



xx(i,j)

= 2η

n(i,j)

˙ε

xx(i,j)

. (9.21)

Compute the σ



˙ε

term for the internal basic nodes (see the solid rectangle

in Fig. 9.3(a)) by averaging its values computed at the four surrounding pressure

132 The heat conservation equation

nodes (see open circle in Fig. 9.3(b)). Compute and visualise (pcolor) the shear

heating distribution (log values) for all internal basic nodes by using the following

equation based on Eq. (9.9)

= 2σ



˙ε

+ 2σ

˙ε

. (9.22)

Eq. 9.22 is valid for an incompressible medium in 2D (˙ε



= ˙ε

=−˙ε



−˙ε

, σ



=−σ



An example is in Shear_heating.m.

Exercise 9.4

Compute the adiabatic heating for the same buoyancy driven ﬂow using the fol-

lowing approximate formula derived from Eq. (9.10) under the assumption that

≈

∂P

∂y

≈ ρg

= Tαv

ρg

. (9.23)

Use T = 1300 K and α = 3 × 10

−5

1/K and compute the adiabatic heating for the

internal basic nodes (see solid rectangle in Fig. 9.3(a)). Interpolate the v

velocity

component for these nodes from the two nearest staggered v

-nodes (see grey

circles in Fig. 9.3(a)). Compare the magnitudes of the shear and adiabatic heating.

Sum up the shear and adiabatic heating terms and visualise the results.

An example is in Shear_adiabatic_heating.m.

Numerical solution of the heat

conservation equation

Theory: Discretisation of the heat conservation equation with ﬁnite

differences. Conservative and non-conservative discretisation schemes.

Explicit and implicit solution schemes of the heat conservation equation.

Advective terms: upwind differences, numerical diffusion. Advection

of temperature with markers. Subgrid diffusion. Thermal boundary con-

ditions: constant temperature, constant heat ﬂux, combined boundary

conditions. Numerical implementation of thermal boundary conditions.

Exercises: Programming various thermal boundary conditions. Solving

the heat conservation equation in the case of constant and variable ther-

mal conductivity with explicit and implicit solution schemes. Advecting

temperature with Eulerian schemes and markers.

10.1 Explicit and implicit formulation of the temperature equation

We now start with the numerical formulation and solution of the temperature

equation. Discretisation of this equation with ﬁnite differences can be done in

an explicit and an implicit manner. In order to understand the differences, let us

consider an example of heat diffusion in a non-deforming medium with constant

thermal conductivity (k)

∂T

∂t

ρC

T . (10.1)

In 2D, this discretisation is as follows.

Explicit FD (Fig. 10.1):

− T

t

ρC



− 2T

+ T

x

− 2T

+ T

y



. (10.2)

133

134 Numerical solution of the heat conservation equation

Fig. 10.1 Stencil of the 2D grid used for an explicit discretisation of the temperature

equation with constant thermal conductivity.

This form is called explicit because the new temperature (T

) at the next time instant

can be explicitly calculated from the known temperatures (T

) at the current time

instant t

= t

+ t,wheret is time step):

kt

ρC



− 2T

+ T

x

− 2T

+ T

y



+ T

. (10.3)

The explicit formulation does not require composing and solving of a global system

of equations and is therefore very convenient to program. However, this formulation

has a strong limitation on the time step that can be used in the calculations. The

time step must satisfy,

t <

x

3κ

, (10.4)

where κ =

ρC

is thermal diffusivity and x is the minimum grid spacing. This

limitation means that the number of time steps increases as the square of the

decrease in the grid spacing, which can be quite inconvenient for high-resolution

thermal models. If larger time steps are indeed employed, numerical oscillations

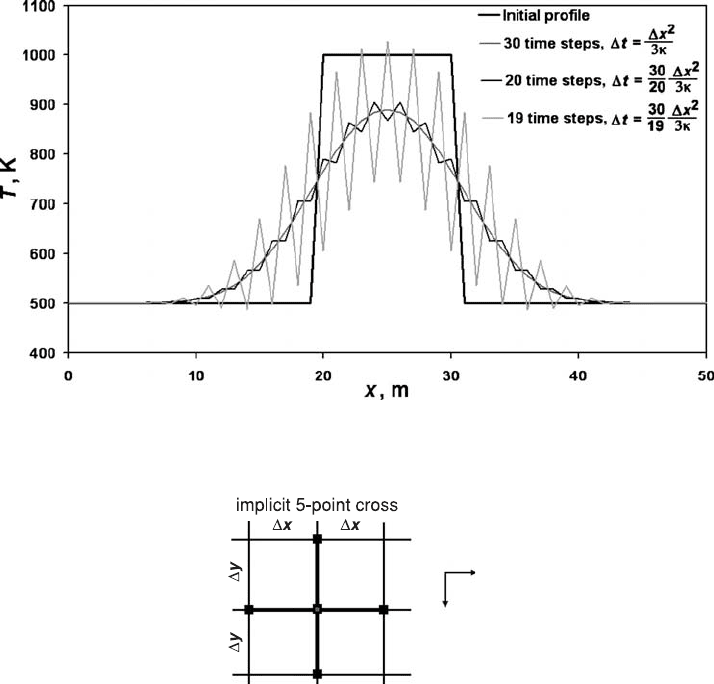
occur that increase with the number of time steps (Fig. 10.2, see also program

example Explicit_implicit_1D.m).

The implicit ﬁnite-difference discretisation is given by (Fig. 10.3):

− T

t

ρC



− 2T

+ T

x

− 2T

+ T

y



. (10.5)

This form is called implicit because the new temperature (T

) for the next time

instant t

cannot be explicitly calculated from the temperatures (T

) known from

the current time instant. In order to obtain new temperatures, the global system of

equations written for all points of the model has to be solved:

t

−

ρC



− 2T

+ T

x

− 2T

+ T

y



t

. (10.6)

10.2 Conservative ﬁnite differences 135

Fig. 10.2 Oscillations of explicit numerical solution of Equation (10.1) due to the

use of a too large time step. An example is in Explicit_implicit_1D.m.

Fig. 10.3 Stencil of the 2D grid used for implicit discretisation of the temperature

equation with constant thermal conductivity.

It is important to mention that the implicit formulation places no limitation on the

size of the time step (in the absence of internal heat sources and advective terms).

Indeed, very large implicit time steps do not necessarily guarantee an accurate

solution (since the time derivative in Eq. (10.5) is only ﬁrst-order accurate in time.

10.2 Conservative ﬁnite differences

Conservative ﬁnite-difference discretisation should be used in cases when the

heat conservation equation contains a variable thermal conductivity. Such ﬁnite

differences ensure conservation of heat ﬂuxes between nodal points, so allowing a

correct numerical solution. In a general sense, this is analogous to the formulation of

conservative ﬁnite differences for the Stokes equation with variable viscosity, which

136 Numerical solution of the heat conservation equation

1A2B3 C 4

∆x

Fig. 10.4 1D staggered grid used for the discretisation of the temperature equation

with variable thermal conductivity. 1, 2, 3, 4 are basic nodes (squares) of the grid

where the temperature equations are formulated. A, B, C are additional nodes

(circles) of the grid where the heat ﬂuxes are deﬁned.

was described in Chapter 7. Below, examples of non-conservative and conservative

ﬁnite differences are compared for the 1D heat conservation equation (Fig. 10.4)

ρC

=−

∂q

∂x

where q

=−k

∂T

∂x

An erroneous non-conservative FD formulation of the heat ﬂux terms, in either

the explicit or the implicit formulation, for the two basic nodes 2 and 3 can for

example be obtained (we can ‘arrive’ at this equation by assuming erroneously

that all we need to do is to use Eq. 10.5 and put different thermal conductivity for

different nodes):

node 2:



∂q

∂x



=−k

(

− T

)

/x

−

(

− T

)

/x

(x

+ x

)/2

(10.7a)

node 3:



∂q

∂x



=−k

(

− T

)

/x

−

(

− T

)

/x

(x

+ x

)/2

, (10.7b)

which implicitly means that the formulations of the horizontal heat ﬂux q

for

temperature equations at nodes 2 and 3 are different due to the different thermal

conductivities k

and k

node 2: q

=−k

− T

x

node 3: q

=−k

− T

x

This implies that heat ﬂux is not conserved and artiﬁcially ‘jumps’ between basic

nodes in response to the difference in the thermal conductivity at these nodes.

On the other hand, a proper conservative FD formulation of the heat ﬂux term

in either the explicit or implicit temperature equations for the two basic nodes 2