Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

7.5 Indexing of unknowns 97

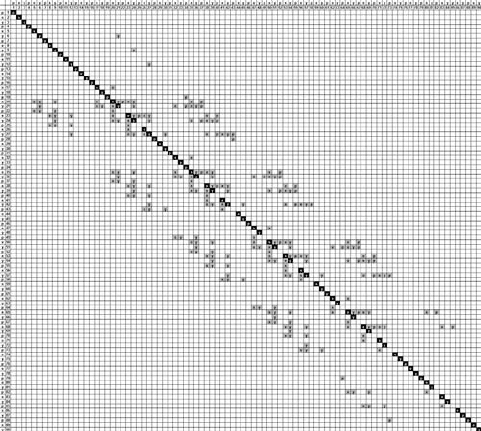
Fig. 7.16 Sparse tri-diagonal global 90 ×90 matrix corresponding to the staggered

grid shown in Fig. 7.15. Coloured rectangles correspond to non-zero coefﬁcients.

Black rectangles are located on the main diagonal of the matrix. Note the absence

of coefﬁcients on the main diagonal when the continuity equation is solved in

order to obtain pressure.

where in

, in

and in

are indices for P, v

and v

related to the given basic node

node

As one can see on Fig. 7.15, index in

located in the centre of a grid cell is always

bigger then the indices in

and in

for the velocity nodes surrounding this cell.

This is an important condition since pressure is obtained by solving the continuity

equation. An incompressible continuity equation does not initially contain pressure

and the solution is guaranteed by the order of processing during the inversion of

the global matrix (Fig. 7.16).

The continuity equation (Eq. (1.28)) for pressure in a given cell (cf. Fig. 7.9)

is processed after all Stokes equations (Eq. 5.18) for all surrounding v

-andv

nodes (cf. Figs. 7.11, 7.12) which contain pressure in the cell. For this reason, the

pressure values in the four corners of the grid (cf. pressure nodes 19, 28, 79 and 88 in

Fig. 7.15) cannot be computed from the continuity equation since these pressure

nodes are not used in the formulation of the momentum equation and are surrounded

by v

and v

nodes for which boundary conditions are formulated (cf. nodes

with underlined indices in Fig. 7.15). For these pressure nodes, some boundary

conditions (e.g. horizontal symmetry) should be used instead. Additionally, the

pressure value should be given at one of the remaining pressure nodes (cf. P-node

98 Numerical solutions of the equations

34 in Fig. 7.15) of the grid such that absolute pressure values can be deﬁned

through the pressure gradients present in the momentum equation. We thus need to

formulate boundary conditions for ﬁve pressure nodes.

The idea about obtaining a solution for pressure by formulating an equation that

does not contain pressure may sound bizarre. Let us just convince ourselves on a

simple example. We apply Gaussian elimination (Eqs. 3.12–3.18) to the analogue

system of three equations with variables v

, v

and P having the global indices 1,

2 and 3 respectively

equation A1 (formulated for v

): 2v

+ 4v

+ 2P = 10,

equation A2 (formulated for v

): 3v

+ 9v

+ 6P = 21,

equation A3 (formulated for P ): v

+ 3v

= 5.

Dividing all equations by a number to normalise the coefﬁcient of v

,weget

equation B1: v

+ 2v

+ P = 5,

equation B2: v

+ 3v

+ 2P = 7,

equation B3: v

+ 3v

= 5.

Eliminating v

by subtracting equation B1 from B2 and B3 yields

equation B1: v

+ 2v

+ P = 5,

equation C2: v

+ P = 2,

equation C3: v

− P = 0.

Note that after the elimination operation, P indeed appears in equation C3.

Eliminating v

by subtracting equation C2 from C3 yields

equation B1: v

+ 2v

+ P = 5,

equation C2: v

+ P = 2,

equation D3: −2P =−2,

Obtaining the solution for P from equation D3

P =−2/(−2) = 1.

Obtaining solution for v

from equation C2

= 2 − P = 2 −1 = 1.

Obtaining the solution for v

from equation B1

= 5 − 2v

− P = 5 − 2 − 1 = 2.

7.5 Indexing of unknowns 99

So it works and we obtained all the required solutions, including one for P by

the Gaussian elimination (we could also have inferred this from the fact that

we have three equations for the three unknowns v

, v

and P). Of course, it

would be impossible to apply (without reordering of equations and re-indexing of

unknowns) the same Gaussian elimination approach if the order of global indices

(and respectively equations) was inverted, i.e.

equation 1 (formulated for P ): 3v

+ v

= 5,

equation 2 (formulated for v

): 6P + 9v

+ 3v

= 21,

equation 3 (formulated for v

): 2P + 4v

+ 2v

= 10.

It should be mentioned, however, that more advanced direct solvers (including ‘\’

command of MATLAB) have internal re-ordering procedures that allow one to

obtain solutions in the latter case as well.

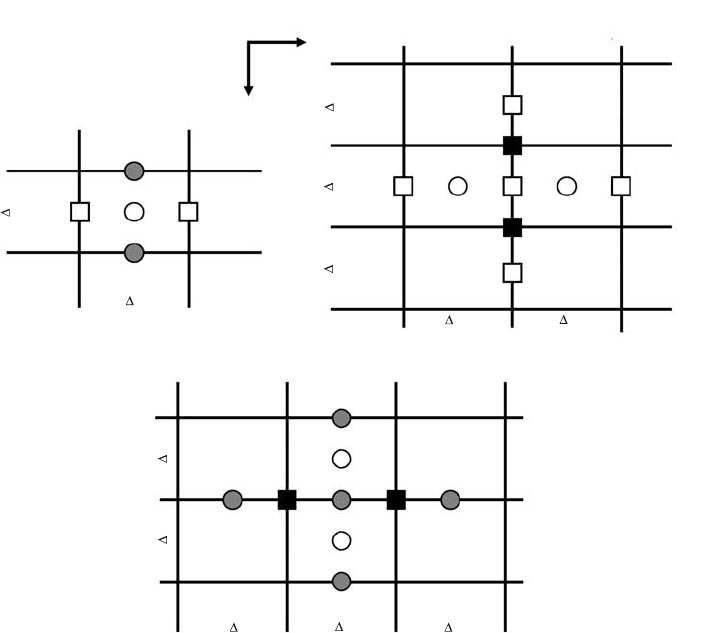
An alternative staggered grid structure uses ghost velocity nodes to formulate

boundary condition equations for v

and v

velocity components (Fig. 7.17). These

equations are not explicitly added to the global matrix and therefore the respective

unknowns for the ghost nodes are not indexed. Instead, these boundary condition

equations are used in an implicit manner by taking them into account while dis-

cretising the momentum and continuity equations for the internal nodes of the grid

located next to the ghost nodes. Values of v

and v

velocities in the ghost nodes are

recovered from the boundary condition equations after obtaining a global solution

for internal nodes. The manner of indexing unknowns is shown in Fig. 7.17 and

again is based on a convention that relates staggered nodes to (part of) the basic

nodes of the grid, numbered as

node

= (j −1) ×(N

− 1) +i,

where in

node

is the index for the given node, i and j are indices for the vertical

and horizontal gridlines intersecting at the considered node (Fig. 7.17). Note that

only (N

− 1) ×(N

− 1) basic nodes are numbered. Unknowns attached for each

numbered basic node are indexed respectively from 1 to (N

− 1) ×(N

− 1) ×3

according to the increasing basic node index

= 3 × in

node

− 2,

= 3 × in

node

− 1,

= 3 × in

node

This way of indexing again ensures that the index for pressure in a cell is bigger than

the indices for all the velocities surrounding the cell. The main advantage of this

staggered grid structure is that there is a smaller number of unknowns in the global

matrix equal to (N

− 1) × (N

− 1) × 3. In addition, the boundary condition for

100 Numerical solutions of the equations

Fig. 7.17 Indexing of unknowns (P, v

and v

)for6×5 2D staggered grid with

the use of ‘ghost velocity nodes’. Dotted lines show the relationship of the stag-

gered nodes to the basic nodes of the grid (note that only part of the nodes is

numbered). Underlined indices denote parameters for which boundary conditions

are deﬁned. Over-lined indices correspond to the ‘ghost unknowns’, which are

introduced for the uniformity of numbering but not used in the numerical solution

(these unknowns are simply set to zero). Empty symbols correspond to the ghost

nodes where velocity boundary condition equations are deﬁned. These boundary

condition equations are implicitly used in the numerical solution when formulat-

ing momentum and continuity equations for the internal (numbered) nodes of the

grid located next to the ghost nodes. Indices i and j correspond to the numbering

of gridlines in the vertical and horizontal directions, respectively.

pressure only needs to be deﬁned in a single cell (see ﬁrst cell in the top left corner

in Fig. 7.17). The implementation of ghost nodes, however, requires additional

programming as the formulation of the momentum and continuity equations for

the ‘near-boundary’ nodes must be done in a special manner in order to take into

account variable velocity boundary conditions.

Compared to the stream function approach (Chapter 5), the use of a pressure–

velocity formulation (also called primitive variable formulation) requires three

times more equations for the same grid resolution. The advantages are, however, that

Programming exercises and homework 101

x-Stokes equation stencil

continuity equation stencil

y-Stokes equation stencil

(b)

(c)

(a)

j −1

j−1

−1

j+1

j+2

−1, j−1)

(

−1, j−1)

(

−1, j)

−1

(

i, j

)

(

)

(

−1

)

(

−1

)

(

−1, j )

(

−1

)

+1,

+1+1

)

(

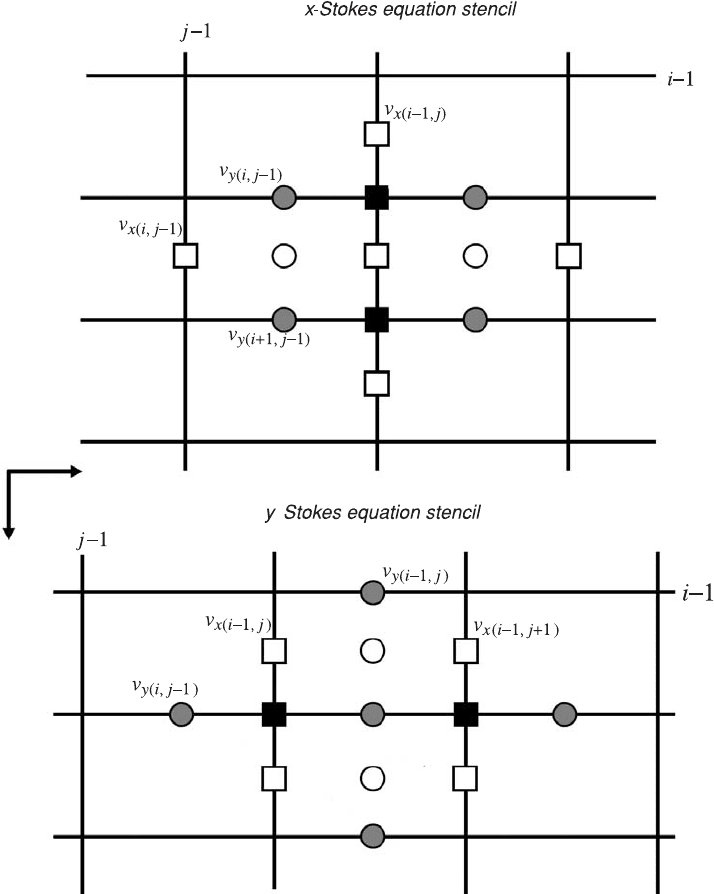
Fig. 7.18 Stencils used for the discretisation of the continuity (a) and Stokes (b),(c)

equations on a 2D regular staggered grid for models with constant viscosity based

on the pressure–velocity formulation. Indexing of gridlines corresponds to basic

(density) nodal points. Indexing of different unknowns is made according to

Fig. 7.15.

the solution for pressure is obtained and that lower (second) order derivatives are

required compared to the fourth-order derivatives required by the stream function-

based equation (5.36).

Programming exercises and homework

Exercise 7.1

Solve the momentum and continuity equations with ﬁnite differences for the

case of constant viscosity using a pressure–velocity formulation (Eqs. (5.22),

(1.28)) on a regular staggered grid (Figs. 7.15, 7.18)of31× 21 points. Program

the numerical model for buoyancy-driven ﬂow in a purely vertical gravity ﬁeld

= 0, g

= 10 m/s

in Eq. 5.22) for a density structure with two vertical layers

(3200 kg/m

and 3300 kg/m

for the left and right layer, respectively). The model

102 Numerical solutions of the equations

size is 1000 ×1500 km (i.e. 1 000 000 ×1 500 000 m). Use constant viscosity

η = 10

Pa s for the entire model.

Compose the matrix of coefﬁcients {L}, the right-hand side vector {R} and

obtain the solution vector {S} with the direct solver (S = L\R) using relations

(7.17) and Fig. 7.15 for global indexing of the unknowns. Boundary conditions

for the velocity are free slip on all boundaries (Eq. 7.15). Boundary conditions for

pressure at the four corners is horizontal symmetry

∂P

∂x

= 0, i.e. pressure is the

same as in the neighbouring cells in the horizontal direction. Boundary condition

for pressure in the additional cell (i = 2andj = 3, Fig. 7.15)isP = 0. Do not

forget that the equations for all ghost unknowns (P =0, v

=0, v

=0) should also

be added to the matrix of coefﬁcients {L} and right-hand side {R} (see over-lined

numbers in Fig. 7.15 for indexing of these unknowns).

The ﬁnite-difference representation of the momentum and continuity equa-

tions in 2D are formulated by analogy to Eqs. (3.20), (7.5)and(7.6) and follows

(Fig. 7.18)

x(i,j−1)

− 2v

x(i,j)

+ v

x(i,j+1)

x

+ η

x(i−1,j )

− 2v

x(i,j)

+ v

x(i+1,j )

y

−K

cont



i+1,j +1

− P



i+1,j

x

= 0, (7.18)

y(i,j−1)

− 2v

y(i,j)

+ v

y(i,j+1)

x

+ η

y(i−1,j )

− 2v

y(i,j)

+ v

y(i+1,j )

y

−K

cont



i+1,j +1

− P



i,j+1

y

=−g

i,j

+ ρ

i,j+1

, (7.19)

cont



x(i−1,j )

− v

x(i−1,j −1)

x

y(i,j−1)

− v

y(i−1,j −1)

y



= 0, (7.20)

where the scaled pressure P



cont

and coefﬁcients K

cont

2η

x + y

are used

to ensure relatively uniform (i.e. not differing by many orders of magnitude) coef-

ﬁcients in all equations. Similarly, both the left and right parts of all boundary

condition equations should be multiplied by a coefﬁcient K

bond

4η

(

x + y

)

This scaling helps obtaining an accurate solution when direct solvers are applied for

models with large viscosities. After solving the global matrix for the velocity com-

ponents and scaled pressure P



, the unscaled pressure is computed as P = P



cont

After obtaining a solution for velocity on staggered nodes, compute the velocity

components v

and v

for the internal basic nodes of the grid (i.e. for 29 ×19 points)

by averaging velocity from surrounding staggered nodes (use the two nearest

velocity nodes for each component). Plot the results for pressure (pcolor)and

Programming exercises and homework 103

i+1, j

x(i, j )

y(i+1, j )

x(i+1, j )

y(i, j )

x(i, j )

y(i, j+1 )

y(i+1, j )

x(i, j+1 )

x(i, j +1)

s(i,j)

n(i+1,j)

n(i, j +1)

n(i+1, j+1)

s(i, j+1)

s(i, j)

i, j

i, j+1

s(i+1, j)

y(i, j)

i,j

∆y

∆x

∆y

∆x ∆x

∆x

j+1

j+2j+1

i+1

i+2

i+1

(b)

(a)

i+1, j

i, j+1

i+1, j +1

i+1, j+1

n(i+1, j+1)

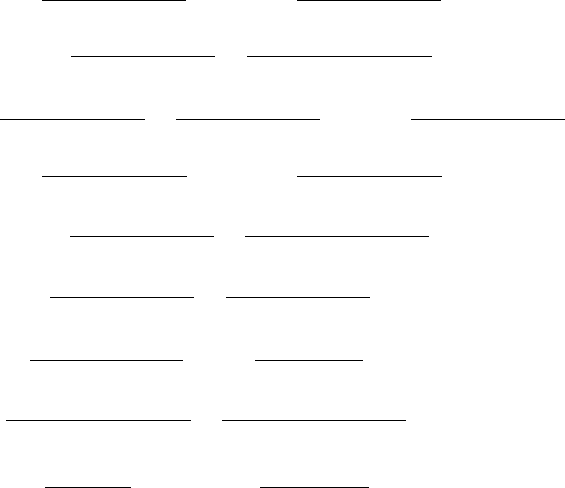
Fig. 7.19 Stencils used for the discretisation of the Stokes equations on a 2D

regular staggered grid for models with variable viscosity based on pressure–

velocity formulation. Indexing of gridlines corresponds to basic (density) nodal

points. Indexing of different unknowns is made according to Fig. 7.15.

104 Numerical solutions of the equations

velocity (quiver) on the same diagram with the vertical axis directed downward

(axis ij).

An example is in Stokes_continuity_constant_viscosity.m.

Exercise 7.2

Modify the previous example for a variable viscosity case. Use different viscosities

for the two vertical layers (10

Pa s and 10

Pa s for the left and right layer,

respectively). Deﬁne the viscosity both at the basic nodes (η

) and at the centres of

cells (η

)(Fig. 7.19). Indexing for the later one should be the same as for pressure

nodes (Fig. 7.15).

The ﬁnite-difference representation of the continuity equation is the same as

before (Eq. 7.20). Stokes equations are formulated by analogy with Eqs. (7.5)and

(7.6) as follows (Fig. 7.19)

2η

n(i+1,j +1)

x(i,j+1)

− v

x(i,j)

x

− 2η

n(i+1,j )

x(i,j)

− v

x(i,j−1)

x

+η

s(i+1,j )



x(i+1,j )

− v

x(i,j)

y

y(i+1,j )

− v

y(i+1,j −1)

xy



− η

s(i,j)

(7.21)



x(i,j)

− v

x(i−1,j )

y

y(i,j)

− v

y(i,j−1)

xy



− K

cont



i+1,j +1

− P



i+1,j

x

= 0

2η

n(i+1,j +1)

y(i+1,j )

− v

y(i,j)

y

− 2η

n(i,j+1)

y(i,j)

− v

y(i−1,j )

y

+η

s(i,j+1)



y(i,j+1)

− v

y(i,j)

x

x(i,j+1)

− v

x(i−1,j +1)

xy



(7.22)

−η

s(i,j)



y(i,j)

− v

y(i,j−1)

x

x(i,j)

− v

x(i−1,j )

xy



−K

cont



i+1,j +1

− P



i,j+1

y

=−g

i,j

+ ρ

i,j+1

cont



x(i−1,j )

− v

x(i−1,j −1)

x

y(i,j−1)

− v

y(i−1,j −1)

y



= 0, (7.23)

where K

cont

2η

min

x + y

and K

bond

4η

min

(

x + y

)

(computed with the value of

minimal viscosity in the model, η

min

) are again used for scaling the coefﬁcients.

An example is in Stokes_continuity_variable_viscosity.m.

The advection equation

and marker-in-cell method

Theory: Advection equation. Solution methods for continuous and dis-

continuous variables. Eulerian schemes: upwind differences, higher-

order schemes, ﬂux corrected transport (FCT). Lagrangian schemes:

marker-in-cell method. Runge–Kutta advection schemes. Numerical

interpolation schemes between markers and nodes.

Exercises: Programming of various advection schemes and markers

8.1 Advection equation

As we already know, the deformation of a continuum changes the spatial distribution

of physical properties. These changes can be described by the advection equation.

For a scalar function (A) at an Eulerian point, this equation is written as follows:

∂A

∂t

=−v · grad

(

)

(8.1a)

or in 3D,

∂A

∂t

=−v



∂A

∂x



− v



∂A

∂y



− v



∂A

∂z



(8.1b)

For a Lagrangian point, the following advection equation relates changes in its

coordinates with material velocities v = (v

);

= v

, (8.2a)

or in 3D,

= v

, (8.2b)

= v

, (8.2c)

= v

, (8.2d)

where i is a coordinate index and x

is a spatial coordinate.

105

106 The advection equation and marker-in-cell method

Exact solution t x/v

Numerical solution t = 0.5 x/v

t = 1.01 x/v

Numerical solution t = 0.25 x/v

t = 0

t = 10

t = 20

t = 0

t = 10

t = 20

(b)

(d)

(a)

(c)

= 1

x = 1

x, m x, m

x = 1

3100

3000

2900

2800

2700

2600

2500

2400

3100

3000

2900

2800

2700

2600

2500

2400

3100

3000

2900

2800

2700

2600

2500

2400

3100

3000

2900

2800

2700

2600

2500

2400

0 5 10 15 20 25 30 35 400 5 10 15 20 25 30 35 40

0 5 10 15 20 25 30 35 40

, kg/m

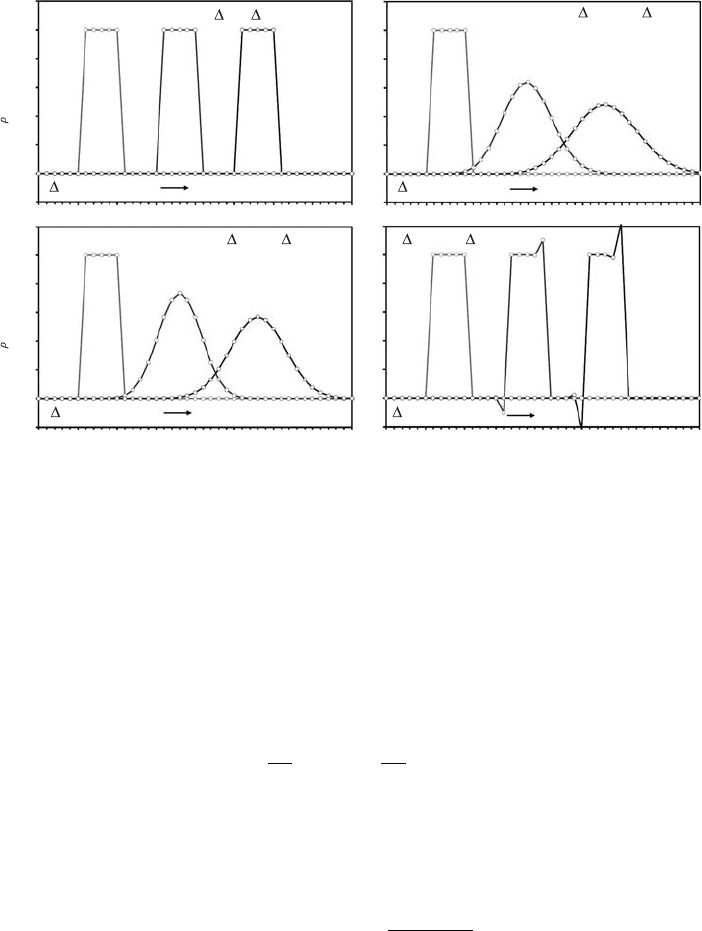
Fig. 8.1 Numerical solutions for the advection of a sharp density wave (i.e.

perturbation) obtained using upwind ﬁnite differences with different size time

steps, t.

8.2 Eulerian advection methods

The advection equations appear trivial, but this is an apparent simplicity. Solving

themnumericallyoftencausesproblems(headaches...).Onesuchproblemisthe

numerical diffusion of sharp gradients during advection. To illustrate the problem,

we solve

∂ρ

∂t

=−v



∂ρ

∂x



, (8.3)

on a regular Eulerian 1D grid with constant spacing between the nodes (x = 1),

for the case of constant material velocity (v

= 1) by applying upwind differences

(Fig. 8.2(a))

t+t

= ρ

− v

t

− ρ

i−1

x

, (8.4)

and using different values of the time step t. Figure 8.1(b) demonstrates how a

sharp density wave (i.e. perturbation) smoothes out (diffuses) during the numerical

solution of a 1D advection equation obtained using upwind ﬁnite differences.

The intensity of the numerical diffusion depends on the number of numeri-

cal steps performed and not on the absolute time of advection (Fig. 8.1(b), (c)).