Gerya T. Introduction to Numerical Geodynamic Modelling
Подождите немного. Документ загружается.


8.3 Marker-in-cell techniques 117
m-th-
marker
i
x
y
j
j+1
B
i,j
B
i+1,j
B
i+1,j+1
B
i,j+1
i+1
x
x
m
y
m
y
Fig. 8.9 Stencil of a 2D grid used for the interpolation of physical properties from
nodes to markers.
Such a local interpolation of properties from markers to nodes, has in many cases,
an effect similar to increasing the Eulerian grid resolution.
Interpolation of physical parameters (e.g., velocity, pressure) from the
Eulerian nodes to Lagrangian markers and other geometrical points is also com-
monly required. One of the simplest methods is to use values of the physical
parameter B, defined at the four Eulerian nodes surrounding a given marker (or any
other geometric point). An effective value of the parameter B for the m-th-marker
can then be calculated using the first-order bilinear interpolation scheme as follows
B
m
= B
i,j
1 −
x
m
x
1 −
y
m
y
+ B
i,j+1
x
m
x
1 −
y
m
y
(8.19)
+B
i+1,j
1 −
x
m
x
y
m
y
+ B
i+1,j +1
x
m
y
m
xy
,
where B
m
denotes the value of the parameter B for the m-th-marker. If one uses an
irregularly spaced grid, the indices of the four nodal points that surround a given
marker (Fig. 8.9) cannot be calculated directly, as in the case of a regular grid.
In this case, a bisection procedure (Fig. 8.10) can be used to define the indices of
the two nearest vertical and horizontal grid lines that bound the cell which contain
the marker (Fig. 8.9). An alternative, faster approach (which however requires
additional memory) is to store the unique cell index for each marker and update it
at every time step by checking only the nearest grid lines.
It should also be mentioned that performing interpolation between nodes and
markers does introduce numerical diffusion. This problem becomes particularly
significant when it is required to interpolate the same time-dependent physical
parameter (e.g., temperature or stress), back and forth between the markers and
nodes. Such diffusion can indeed be minimised by interpolating incremental values

118 The advection equation and marker-in-cell method
Fig. 8.10 Finding two nearest grid lines around the marker (open square) by a
bisection algorithm in the case of an irregularly spaced grid. The search starts by
having the first (line 1) and last (line 15) lines of the grid as leftmost (L = 1)
and rightmost (R = 15) limits for the bisection. At each check, the middle line
M = (L +R)/2 is defined and its horizontal position is compared with that of
the marker. Depending on the result of the comparison, line M becomes either L
(when M is to the left of the marker) or R (when M is to the right of the marker).
The check continues until the difference in the index between L and R become
one. The required number of checks (n) is given by the relation 2
n
= N, where N
is number of grid lines.
Interpolation of absolute values Interpolation of increments
(a)
B
xx
new B new B
old B
nodes nodes
markers markers
old B
B
(b)
Fig. 8.11 Interpolation of the absolute values of the parameter B (a) and its incre-
ments (b) from nodes to markers. Note that the interpolation of increments does
not smooth out subgrid variations of B onto the markers.

Programming exercises and homework 119
and not absolute values of the parameter from the nodes to the markers (Figs. 8.9,
8.11).
B
t+t
m
= B
t
m
+
B
t+t
i,j
− B
t
i,j
1 −
x
m
x
1 −
y
m
y
+
B
t+t
i,j+1
− B
t
i,j+1
×
x
m
x
1 −
y
m
y
+
B
t+t
i+1,j
− B
t
i+1,j
1 −
x
m
x
y
m
y
+
B
t+t
i+1,j +1
− B
t
i+1,j +1
x
m
y
m
xy
, (8.20)
where indices t and t +t correspond to the current and next time instant,
respectively.
Programming exercises and homework
Exercise 8.1
Program and compare the simple Eulerian advection schemes (upwind, central and
downwind FD, Eqs. (8.4), (8.8), (8.9) in 1D for the case illustrated in Fig. 8.6.The
model resolution is 151 nodal points. Other parameters are the same as in Fig. 8.6.
An example is in Upwind_1D.m.
Exercise 8.2
Program and compare the FCT method and the marker-in-cell schemes in 1D for
the same model. Use 5 markers per cell (200 markers for the entire model) and
‘recycle’ markers which leave the model from one side by adding them to the other
side (periodic boundary condition). To recycle markers, update their coordinate as
follows: for markers that leave the model through the right boundary and appear at
the left boundary, set
x
recycled
m
= x
m
− L, (8.21a)
For markers that leave the model through the left boundary and enter it at the right
boundary, set
x
recycled
m
= x
m
+ L, (8.21b)
where x
m
,x
recycled
m
are marker coordinates before and after recycling, respectively.
Use the following formula to define the index j (smallest index is 1) of the nearest
node to the left of the marker from its coordinate
j = int
x
m
x
+ 1, (8.22)
where x
m
is the marker coordinate, x is the nodal (Eulerian) grid space, int()
is a function which returns the integer part of a value. Two possible MATLAB
120 The advection equation and marker-in-cell method
implementations of Eq. (8.22)are
i = double(int16(xm/dx − 0.5)) +1;
i = double(int16(xm/dx + 0.5));
Examples are in FCT_1D.m and Markers_1D.m.
Exercise 8.3
Modify the previous marker-based code by introducing non-uniform distances
between nodal points and markers and by using a bisection algorithm (Fig. 8.10)
to define indices of the nearest nodes. Prescribe a slightly variable velocity on the
nodal points and interpolate it to markers when displacing them. An example is
given in Markers_1Dirregular.m associated with this chapter.
Exercise 8.4
Modify the 2D model with the variable viscosity (Exercise 7.2) by including the
advection of density and viscosity fields with markers. Create a grid of 200 ×300
markers with small (up to half of the marker grid distance) random displacements
(rand) relative to regular positions. Randomisation is introduced to prevent the
opening of big gaps between markers during the simulation which often occurs if
regular marker grids are used (e.g. due to pure-shear-related stretching that increases
the distances between markers). Save the horizontal and vertical coordinate for
every marker and assign it with the density and viscosity depending on the position
in either the left or the right layer. An alternative approach, which requires less
memory, is to assign every marker with a material type index depending on the
initial position (i.e. 1 and 2 for the left and right layer, respectively). Then the marker
density and viscosity (and potentially any other material-dependent property) can
be estimated based on the material type index. Interpolate the marker density and
viscosity (η
s
in Fig. 7.19) to the basic nodes of the grid using Eq. (8.18) (write
a loop over the markers and add the density and viscosity of each marker to the
four surrounding nodes, Fig. 8.9). For computing i and j indices for the upper left
node next to the marker (Fig. 8.9), apply Eq. (8.22) separately for each coordinate.
Compute the viscosity for the centres of cells (η
n
in Fig. 7.19) by averaging the
viscosity from the four surrounding basic nodes (an alternative way is to interpolate
this viscosity directly from markers based on Eq. 8.18). After obtaining a velocity
field, define a time step in such a manner that the marker displacements do not
exceed half the grid spacing. Interpolate the v
x
and v
y
velocity components for the
markers from the staggered nodes (Eq. 8.19) and displace them using a first-order
accurate scheme (Eq. (8.13)). Note that for staggered nodes, Eq. (8.22) is modified
since these nodes are displaced by half of the grid distance relative to the basic

Programming exercises and homework 121
ones
i = int
y
m
− y /2
y
+ 1 (for v
x
nodes), (8.23a)
j = int
x
m
− x/2
x
+ 1 (for v
y
nodes). (8.23b)
Use a uniform velocity interpolation procedure for all markers, including those
outside of the grids of staggered v
x
-andv
y
-nodes (e.g. above the first line of
v
x
-nodes, within half of vertical grid step from the top of the model, Fig. 7.15).
In the latter case, the marker will be located outside the 4-node cell (Fig. 8.9)
and normalised distances x
m
/x and y
m
/y to the upper left node of the cell
in Eq. (8.19) can be either negative or larger than 1. The velocity will indeed be
interpolated properly, and will be consistent with the boundary conditions. After
displacing all the markers, go to the next time step and interpolate the density
and viscosity to the nodes using the new markers positions. An example is in
Stokes_Continuity_Markers.m.
Exercise 8.5
Update the 2D code developed above to use a fourth-order Runge–Kutta
scheme (Eqs. (8.14), (8.17)) for marker displacement. An example is in
Stokes_Continuity_Markers_Runge_Kutta.m.

9
The heat conservation equation
Theory: Fourier’s law of heat conduction. Heat conservation equa-
tion and its derivation. Radioactive, viscous and adiabatic heating and
their relative importance. Heat conservation equation for the case of a
constant thermal conductivity and its relation to the Poisson equation.
Analytical examples: steady geotherm and steady temperature profile
in case of channel flow.
Exercises: Computing shear heating and adiabatic heating distribution
for buoyancy driven flow.
9.1 Fourier’s law of heat conduction
Heat transport plays a crucial role in geodynamics and is often inherently coupled to
material deformation, as for example in mantle convection, granitic cupola growth,
subduction etc. Let us first study the equations relevant to heat transport processes.
The most basic one is Fourier’s law of heat conduction, which relates the heat flux
q, (W/m
2
) to the temperature gradient
∂T
∂x
(K/m) according to
q =−k
∂T
∂x
, (9.1)
where k (W/m/K) is the thermal conductivity of the material. Thermal conductivity
may depend on P, T, composition and structure of the material. The heat flux q is
the amount of heat that passes through a unit surface area, per unit time. As we all
know, heat is always transferred from a hot body to a colder one. This is reflected
by the minus sign in the right part of Equation (9.1), which implies that heat flux
is positive in the direction of decreasing temperature, i.e. in the case when the
temperature gradient
∂T
∂x
is negative. In three dimensions, the heat flux is a vector
123

124 The heat conservation equation
that can be decomposed into three components
q = (q
x
,q
y
,q
z
).
In this case, Fourier’s law relates heat fluxes in different directions to the respective
temperature gradients
q =−k∇T or q
i
=−k
∂T
∂x
i
, (9.2)
where i is a coordinate index and x
i
is a spatial coordinate, or
q
x
=−k
∂T
∂x
,
q
y
=−k
∂T
∂y
,
q
z
=−k
∂T
∂z
.
9.2 Heat conservation equation
In order to predict changes in temperature due to heat transport, the heat conser-
vation equation, also called temperature equation, has to be solved. This equation
describes the balance of heat in a continuum and relates temperature changes due
to internal heat generation, as well as with advective and conductive heat transport.
The Lagrangian temperature equation has the following form
ρC
P
DT
Dt
=−
∂q
i
∂x
i
+ H, (9.3)
or spelled out in a complete 3D form
ρC
P
DT
Dt
=−
∂q
x
∂x
−
∂q
y
∂y
−
∂q
z
∂z
+ H,
or by using Equation (9.2)
ρC
P
DT
Dt
=
∂
∂x
k
∂T
∂x
+
∂
∂y
k
∂T
∂y
+
∂
∂z
k
∂T
∂z
+ H,
where the repeated index i, means a summation of derivatives of heat flux compo-
nents by respective coordinates (x, y, z); ρ is density (kg/m
3
); C
P
is heat capac-
ity at constant pressure (J/kg/K); H is volumetric heat productions (W/m
3
).
DT
Dt
is the substantive time derivative of temperature corresponding to the standard
9.2 Heat conservation equation 125
Lagrangian–Eulerian relation, which was already discussed in Chapters 1 and 5
DT
Dt
=
∂T
∂t
+ ¯v · grad(T ).
For example, in 3D
DT
Dt
=
∂T
∂t
+ v
x
∂T
∂x
+ v
y
∂T
∂y
+ v
z
∂T
∂z
.
Accordingly, the temperature equation in an Eulerian form can be written as
follows
ρC
P
∂T
∂t
+ ¯v · grad(T )
=−
∂q
i
∂x
i
+ H, (9.4)
or in complete 3D form as,
ρC
P
∂T
∂t
+ v
x
∂T
∂x
+ v
y
∂T
∂y
+ v
z
∂T
∂z
=−
∂q
x
∂x
−
∂q
y
∂y
−
∂q
z
∂z
+ H,
or by using Equation (9.2)as
ρC
P
∂T
∂t
+ v
x
∂T
∂x
+ v
y
∂T
∂y
+ v
z
∂T
∂z
=
∂
∂x
k
∂T
∂x
+
∂
∂y
k
∂T
∂y
+
∂
∂z
k
∂T
∂z
+ H.
The Lagrangian heat conservation equation can be derived by analysing heat
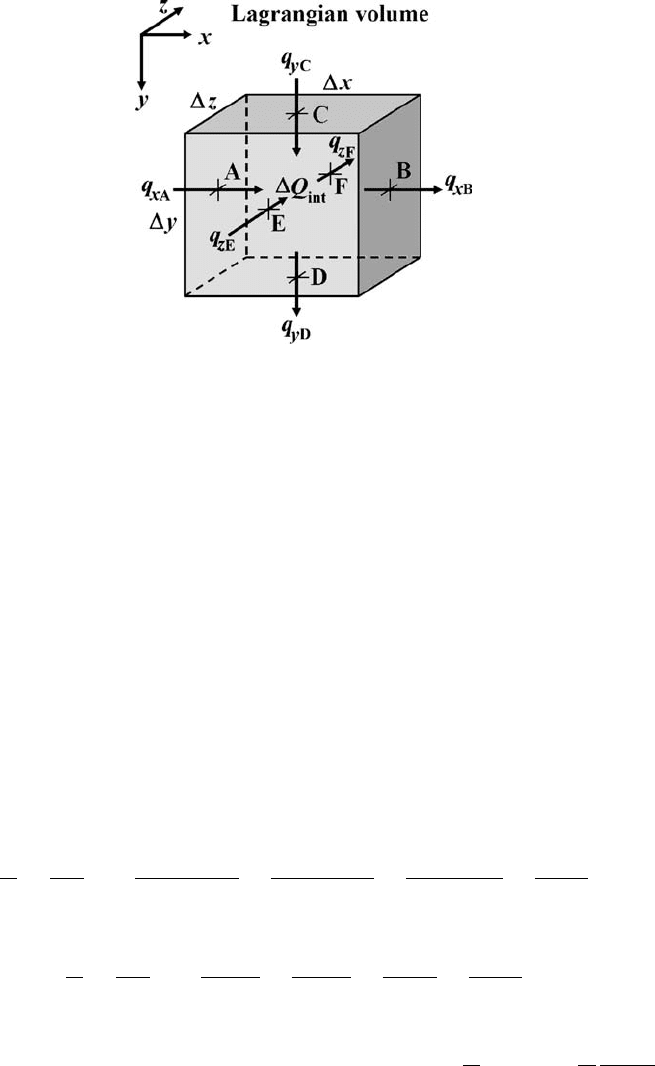
fluxes through the small moving rectangular Lagrangian (material) volume of mass
m and with dimensions x, y and z (Fig. 9.1). Let us assume that the initial
temperature of this volume is T
0
.
Heat comes into the volume through the boundaries A, C and E and leaves the
volume through the opposed boundaries B, D and F respectively. In addition, there
is an internal heat source Q
int
inside the volume. Heat fluxes affect the amount
of heat in the material volume and after a small period of time t, the temperature
changes to T
1
. The amount of heat Q required to change the temperature can be
computed from the following thermodynamic relation
Q = mC
P
T = mC
P
(T
1
− T
0
). (9.4)
In accordance with the energy conservation principle, this amount of heat should
match the bulk effect of various heat sources and sinks in the volume such that
Q = Q
int
+ Q
A
− Q
B
+ Q
C
− Q
D
+ Q
E
− Q
F
, (9.5)
where Q
A
–Q
F
represents the amounts of heat that fluxed through the respective
boundaries during the period of time t. These can be computed according to the
126 The heat conservation equation
Fig. 9.1 Lagrangian elementary volume considered for derivation of the respec-
tive form of the heat conservation equation. Arrows show heat flux components
responsible for heat fluxes through respective boundaries (A, B, C, D, E and F).
definition of heat fluxes as
Q
A
= q
xA
yzt,
Q
B
= q
xB
yzt,
Q
C
= q
yC
xzt,
Q
D
= q
yD
xzt,
Q
E
= q
zE
xyt,
Q
F
= q
zF
xyt,
(9.6)
where q
xA
–q
zF
are the heat flux components responsible for heat fluxes through
respective boundaries (Fig. 9.1).
Equating the right-hand sides of Equations (9.4), (9.5) and dividing through by
t and the volume V = xyz, we obtain the following equation for the energy
conservation in a Lagrangian volume (verify as an exercise)
m
V
C
P
T
t
=−
(
q
xB
− q
xA
)
x
−
(q
yD
− q
yC
)
y
−
(
q
zF
− q
zE
)
z
+
Q
int
Vt
, (9.7a)
or in a different notation
m
V
C
P
T
t
=−
q
xBA
x
−
q
yDC
y
−
q
zFE
z
+
Q
int
Vt
, (9.7b)
where q
xBA
, q
yDC
and q
zFE
are the changes in respective heat fluxes between
respective points. Taking into account the relationships ρ =
m
V
,andH =
1
V
DQ
int
Dt
,
and further assuming that t, x, y and z all tend towards zero, the differences
