Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

Programming exercises and homework 147

Exercise 10.2

Modify the previous example to take into account variable thermal conductivity

using a conservative ﬁnite-difference formulation (Eq. (10.9), Fig. 10.5)fora

uniform grid (i.e. x

= x

= x and y

= y

= y in Eq. (10.9))

P 3

t

−

+ k

)



− T



− (k

+ k

)



− T



2x

−

+ k

)



− T



− (k

+ k

)



− T



2y

= H

+ ρ

P 3

t

(10.25)

Use different physical properties for the area of the temperature wave (k =

10 W/m/K, ρ = 3300 kg/m

, C

= 1100 J/kg/K) and the surrounding medium

(k = 3 W/m/K, ρ = 3200 kg/m

, C

= 1000 J/kg/K). An example is in Variable_

conductivity.m.

Exercise 10.3

Modify the two previous examples by adding the advective terms into the tem-

perature equation (Eq. (10.11)) and by using a uniform velocity ﬁeld v

= 10

−9

m/s and v

= 10

−9

m/s in the entire model. Test Eq. (8.5) for the time step lim-

itation in 1D and reﬁne it for 2D. Experiment with different velocities to see

advection- and conduction-dominated regimes. Observe that the numerical dif-

fusion which is clearly visible when the chosen velocity is large (e.g. v

= 10

m/s and v

= 10 m/s). In this case, the timescale for the experiment will be far

below the characteristic thermal diffusion timescale (compute it by using a pre-

scribed size of the wave and a total time in your experiment, Eq. (9.17), Fig.

9.2) and thus the moving temperature wave should remain largely unchanged.

Examples are in Conduction_advection2D.m and Variable_conductivity_

advection2D.m.

Exercise 10.4

Modify Exercise 10.2 by adding temperature advection with a marker-in-cell

approach combined with subgrid diffusion (Eqs. (10.14)–(10.19)). Use an implicit

solution of the Lagrangian temperature equation (10.12). Use marker routines

from Exercises 8.4 and 8.5. Interpolate density, heat, capacity and temperature

from markers to nodes at every time step using Eq. (8.18). Move the markers with

the prescribed constant velocity and recycle them when they leave the model. Use

Eqs. (8.21a,b) for both the horizontal and vertical coordinates of the markers. Do

not forget to match nodal and marker temperature ﬁelds before starting calcula-

tions (e.g. interpolate the nodal temperature back to the markers after performing

interpolation of nodal temperature from markers for the ﬁrst time). Also do not

148 Numerical solution of the heat conservation equation

forget to apply the boundary conditions for the nodal temperatures interpolated

from the markers at every time step. Experiment with different velocities to see

advection- and conduction-dominated regimes. Compare these results with Exer-

cise 10.3 for the case when the chosen velocities are large, both without (d = 0in

Eq. (10.16)) and with (d = 1inEq.(10.16)) subgrid diffusion. An example is in

Variable_conductivity_markers2D.m.

2D thermomechanical code structure

Theory: Principal steps of a coupled thermomechanical solution with

ﬁnite-differences and marker-in-cell techniques. Organisation of a ther-

momechanical code for the case of viscous, multi-component ﬂows.

Adding self-gravity. Handling free planetary surfaces with a weak layer

approach.

Exercises: Building a 2D thermomechanical code.

11.1 What do we expect from geodynamic codes?

Before describing possible structures for thermomechanical codes, let us discuss

what we actually expect from a state-of-the-art, numerical geodynamic modelling

tool. Today, as numerical modelling of geodynamic and planetary processes is in the

‘new millennium’ (although it is only around 40 years old, see Introduction), geo-

scientists are targeting modelling of realistic situations in lithospheric, mantle and

planetary dynamics (e.g. Gerya and Yuen, 2007; Moresi et al., 2008; Zhong et al.,

2007; Tackley, 2008). The rheology of crustal and mantle rocks depends strongly

on the temperature, strain-rate, volatile content, grain size and the ﬂuid pressure.

Physical and dynamical circumstances imposed by the sharply varying viscosity

represent a major challenge for solving the momentum equation in geodynamics,

unlike those found in the oceanographic or atmospheric sciences. Another compli-

cation is due to the variable thermal conductivity in the heat conservation equation.

The thermal conductivity of various crustal and mantle rocks is notably differ-

ent and is also a strong function of temperature, pressure and mineralogy which

causes numerical difﬁculties compared to the constant thermal conductivity situ-

ation. Finally, all physical (transport) properties of rocks, including viscosity and

conductivity, vary strongly with chemical composition and/or mineralogy. In vari-

ous geodynamic situations, these result in sharp fronts involving multi-component

149

150 2D thermomechanical code structure

ﬂows (i.e. ﬂows composed of many rock types with contrasting compositions

and physical properties). Therefore, from a general geophysical standpoint, we

should consider at least three important elements for modelling these kinds of

ﬂows:

(1) the ability to conserve stresses under conditions that involve sharply discontinuous

viscosity distributions;

(2) the ability to conserve heat ﬂuxes under conditions that involve sharply varying con-

ductivity and temperature gradients at the thermal or chemical layers with temperature-

dependent conductivity;

(3) the ability to conserve transport properties, such as temperature ﬁeld, chemical species,

viscosity and density in ﬂows with a strong advection character.

11.2 Thermomechanical code structure

Since we want to address all above requirements in our state-of-the-art ‘all-in-

one’ thermomechanical code, let us discuss in detail how this can be achieved by

using a marker-in-cell algorithm, combined with a conservative ﬁnite-differences

for primitive variable (pressure–velocity) formulation. The code structure should

reﬂect the physical relations of momentum, continuity, temperature and advection

equations. For example, the temperature equation requires values of adiabatic

and shear heating that are computed from the velocity, pressure, stress and strain

rate ﬁelds. Therefore, the temperature equation can only be solved after solving

the momentum and continuity equations. On the other hand, the momentum and

continuity equations have to be solved simultaneously to obtain values for velocity,

that are present in both equations. The advection equation requires a velocity

ﬁeld and should thus also be solved after solving the momentum and continuity

equations.

The ﬂow chart in Fig. 11.1 gives an example of a structure for a numerical,

thermomechanical viscous 2D code that uses ﬁnite-differences and the marker-

in-cell technique (FD+MIC) to solve the momentum, continuity and temperature

equations. The principal steps of the algorithm are as follows:

(1) Calculating the scalar physical properties (η

, ρ

, α

, C

, k

, etc.) for each marker

and interpolating these properties, as well as advected temperature from the mark-

ers to Eulerian nodes (Chapters 8, 10). Applying boundary conditions for the nodal

temperatures interpolated from markers.

(2) Solving the 2D momentum and continuity equations with a pressure–velocity formu-

lation on a staggered grid by composing and inverting the global matrix with a direct

method, which is used because of its stability and high accuracy (Chapter 7).

(3) Deﬁning an optimal displacement time step t

for markers (typically limiting maxi-

mal displacement to 0.01–1.0 of minimal grid step) based on the velocity ﬁeld computed

in Step 2 (Chapter 8).

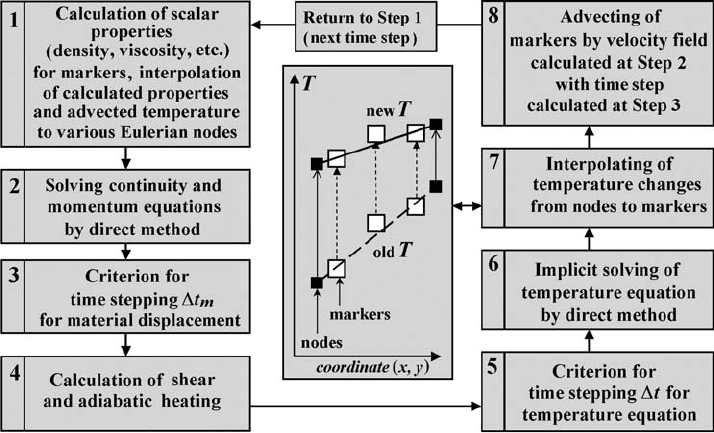
11.2 Thermomechanical code structure 151

Fig. 11.1 Flow chart that gives an example of a possible structure of a numer-

ical thermomechanical viscous 2D code which employs ﬁnite-differences and

marker-in-cell technique (FD +MIC) for solving the momentum, continuity and

temperature equations. (Gerya and Yuen, 2003a).

(4) Calculating the shear and adiabatic heating terms H

s(i, j )

and H

a(i, j )

at the Eulerian

nodes (Chapter 9).

(5) Deﬁning an optimal time step t for the temperature equation. We take the smallest

time step of three time step limiters: given absolute time step limit; given optimal

marker displacement time step limit (see Step 3); given absolute nodal temperature

change limit (typically 1–20 K) (Chapter 10).

(6) Solving the temperature equation in a Lagrangian formulation, with implicit time

stepping and a direct method (Chapter 10).

(7) Interpolating the calculated nodal temperature changes (see Step 7 at Fig. 11.1)from

the Eulerian nodes to the markers and calculating new marker temperatures (T

) taking

into account physical diffusion on subgrid (marker) level (Chapter 10).

(8) Using a fourth-order explicit Runge–Kutta scheme (Chapter 8) in space to advect all

markers throughout the mesh according to the globally calculated velocity ﬁeld v (see

Step 2). Returning to Step 1 to perform the next time step.

Figure 11.2 shows the geometry of an irregularly spaced, fully staggered numerical

grid corresponding to the algorithm outlined above. The irregularly spaced grid is

extremely useful in handling geodynamic situations with localisation phenomena

and multiple-scale features which will be further discussed in Chapters 16 and

17. Note that by doing the programming exercises for previous chapters we have

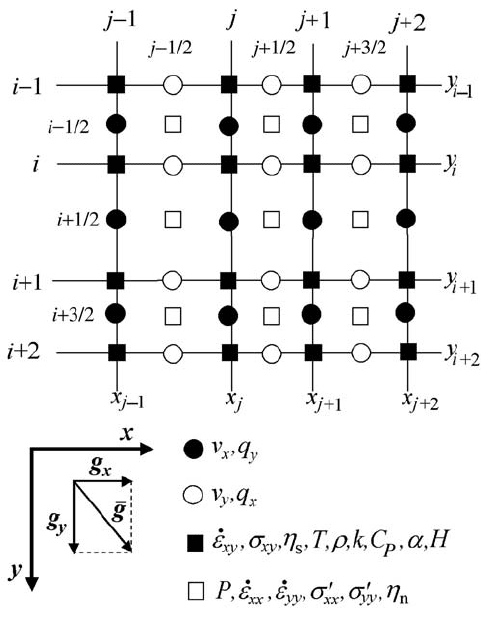
152 2D thermomechanical code structure

Fig. 11.2 Staggered 2D, irregularly spaced numerical grid corresponding to the

algorithm presented in Fig. 11.1.

already implemented (surprise, surprise . . . ) one-by-one all steps of the above

computational algorithm and we will now discuss in full detail how to connect

these separate steps in order to create a state-of-the-art code out of our ‘embryonic’

2D codes. Additional explanations for some of the algorithmic steps are given

below.

Step 1: Interpolation of scalar properties from markers to nodes

According to our algorithmic approach, the temperature ﬁeld and the rock type are

represented by values assigned for the multitude of markers initially distributed on

a ﬁne regular marker mesh with a small (≤1/2 marker grid distance) random dis-

placement. Other scalar properties such as density, viscosity, thermal conductivity

etc. are computed for each marker at every time step in accordance to the rock type

11.2 Thermomechanical code structure 153

associated with each marker. This approach allows us to minimise the amount of

storage associated with markers to only 3 ﬂoating point values (two coordinates

and temperature) and one integer (rock type). The amount of different rock types in

one experiment is typically limited to few tens at most. There are several equations

(rheology, density, etc.) associated with each rock type which allow us to compute

various properties for a marker of a given type, based on the local temperature

and pressure at this marker. The effective values of all these properties at the

Eulerian nodal points are computed from the markers at each time step by using a

bilinear interpolation (Eq. (8.18)). Note that viscosity for shear (η

) and normal (η

)

stresses is interpolated separately (Fig. 11.2) by using a local interpolation scheme

that takes into account markers found within half a grid spacing distance from

the nodes, in both the horizontal and vertical directions (see dashed boundary in

Fig. 8.8). The statistical weights of these markers thus vary from 0.25 to 1 (one

can also renormalise these weights to vary from 0 to 1). The local interpolation

of viscosity allows for a more accurate solution of the momentum equation in the

case of a strongly variable viscosity (Gerya and Yuen, 2007; Schmeling et al.,

2008). All other properties are interpolated to the basic nodes (cf. solid squares

in Fig. 11.2) using a standard scheme that involves markers found in the four

grid cells around each node (Fig. 8.8, Eq. (8.18)). In cases when we require a

more accurate solution of the temperature equation, for example under the con-

dition of a strongly variable thermal conductivity, localised interpolation schemes

from markers should also be used for the thermal conductivity k that will be com-

puted separately for the different heat ﬂux nodes (see solid and open circles in

Fig. 11.2). Thermal boundary conditions should be applied to the obtained nodal

values after interpolating the temperature from markers. This precludes accumulat-

ing an interpolation error which will otherwise grow along the model boundaries

as the number of time steps increases.

We use a standard, ﬁrst-order-accurate bilinear interpolation procedure that

involves four nodal points (Fig. 8.9, Eq. (8.19)) for the reverse problem of inter-

polating scalar properties (including calculated temperature changes), vectors and

tensors from the corresponding Eulerian nodal points (see different types of Eule-

rian nodes in Fig. 11.2), back to the markers and other geometric points (e.g.

other nodes). Equation (8.19) is used uniformly, for interpolating velocity, stresses,

strain rates, pressure, temperature and other properties from nodal points to mark-

ers. Since our staggered grid represents, in fact, the superposition of four simple

rectangular grids corresponding to different scalar ﬁelds, vectors and tensors (see

four different symbols for grid points in Fig. 10.2), these Eulerian grids are used

individually for interpolating the respective ﬁeld variables. Deﬁning the indices

of the four nodal points that surround a given marker is done on the basis of the

bisection procedure (Fig. 8.10).

154 2D thermomechanical code structure

Step 2: Solving the momentum and continuity equations

In 2D, we have two Stokes equations of slow, viscous incompressible ﬂow in a

uniform gravity ﬁeld

x-Stokes equation

∂σ



∂x

∂σ

∂y

−

∂P

∂x

=−ρg

, (11.1)

y-Stokes equation

∂σ



∂y

∂σ

∂x

−

∂P

∂y

=−ρg

, (11.2)



= 2η ˙ε



= 2η ˙ε

= σ

= 2η ˙ε

˙ε

∂v

∂x

˙ε

∂v

∂y

˙ε



∂v

∂y

∂v

∂x



Since by deﬁnition σ



=−σ



and for incompressible ﬂuid ˙ε

=−˙ε

in 2D, we

can also avoid any nodal storage for σ



and ˙ε

and re-formulate Eq. (11.2) in a

different form

−

∂σ



∂y

∂σ

∂x

−

∂P

∂y

=−ρg

. (11.2a)

The conservation of mass is given by the incompressible, 2D continuity equation

∂v

∂x

∂v

∂y

= 0. (11.3)

We use the standard procedure described in Chapter 7 (Figs. 7.11, 7.12,

Eqs. 7.5, 7.6) for the formulation of FD schemes to represent the momentum

equations (11.1) and (11.2) in a conservative form.

The x-Stokes equation is formulated for the horizontal velocity node v

x(i+1/2,j )



∂σ



∂x



i+1/2,j



∂σ

∂y



i+1/2,j

−



∂P

∂x



i+1/2,j

=−

(

ρg

)

i+1/2,j

, (11.4)

or in FD representation



xx(i+1/2,j +1/2)

− σ



xx(i+1/2,j −1/2)

j+1

− x

j−1

xy(i+1,j)

− σ

xy(i,j)

i+1

− y

−2

(i+1/2,j +1/2)

− P

(i+1/2,j −1/2)

j+1

− x

j−1

=−

(i,j)

+ ρ

(i+1,j )

11.2 Thermomechanical code structure 155

where

xy(i,j)

= 2η

s(i,j)



x(i+1/2,j )

− v

x(i−1/2,j )

i+1

− y

i−1

y(i,j+1/2)

− v

y(i,j−1/2)

j+1

− x

j−1



xy(i+1,j)

= 2η

s(i+1,j )



x(i+3/2,j )

− v

x(i+1/2,j )

i+2

− y

y(i+1,j +1/2)

− v

y(i+1,j −1/2)

j+1

− x

j−1



xx(i+1/2,j −1/2)

= 2η

n(i+1/2,j −1/2)

x(i+1/2,j )

− v

x(i+1/2,j −1)

− x

j−1



xx(i+1/2,j +1/2)

= 2η

n(i+1/2,j +1/2)

x(i+1/2,j +1)

− v

x(i+1/2,j )

j+1

− x

where i, i +1/2andj, j +1/2 indices denote, respectively, the vertical and horizon-

tal positions of the nodal points corresponding to the different physical parameters

(Fig. 11.2) within the staggered grid.

The y-Stokes equation is formulated for the vertical velocity node v

y(i,j+1/2)



∂σ



∂y



i,j+1/2



∂σ

∂x



i,j+1/2

−



∂P

∂y



i,j+1/2

=−(ρg

)

i,j+1/2

(11.5)

or in FD representation



yy(i+1/2,j+1/2)

− σ



yy(i−1/2,j+1/2)

i+1

− y

i−1

xy(i,j+1)

− σ

xy(i,j)

j+1

− x

−2

(i+1/2,j +1/2)

− P

(i−1/2,j +1/2)

i+1

− y

i−1

=−

(i,j)

+ ρ

(i,j+1)

where σ

xy(i,j)

is given above for Eq. (11.4)

xy(i,j+1)

= 2η

s(i,j+1)



x(i+1/2,j +1)

− v

x(i−1/2,j +1)

i+1

− y

i−1

y(i,j+3/2)

− v

y(i,j+1/2)

j+2

− x



yy(i−1/2,j+1/2)

= 2η

n(i−1/2,j +1/2)

y(i,j+1/2)

− v

y(i−1,j +1/2)

− y

i−1



yy(i+1/2,j+1/2)

= 2η

n(i+1/2,j +1/2)

y(i+1,j +1/2)

− v

y(i,j+1/2)

i+1

− y

The continuity equation is formulated for the pressure node P

(i−1/2,j −1/2)



∂v

∂x



i−1/2,j −1/2



∂v

∂y



i−1/2,j −1/2

= 0, (11.6)

or in FD representation

x(i−1/2,j )

− v

x(i−1/2,j −1)

− x

j−1

y(i,j−1/2)

− v

y(i−1,j −1/2)

− y

i−1

= 0.

After composing all equations, we invert (i.e. solve) the resulting global matrix

by an accurate, direct method in order to simultaneously solve the momentum

156 2D thermomechanical code structure

equations (11.4)and(11.5) and the continuity equation (11.6), combined with any

boundary conditions for the velocity and pressure (Chapter 7). The momentum

equations (11.4)and(11.5) are solved for v

x(i+1/2,j )

and v

y(i,j+1/2)

, respectively,

while the continuity equation (11.6) is solved for P

(i−1/2,j −1/2)

. The incompressible

continuity equation (11.6) does not initially contain P

(i−1/2,j −1/2)

and, as was

discussed in Chapter 7, the solution is guaranteed by the order of processing during

the inversion of the global matrix based on relating the staggered nodes (open

squares and open and solid circles in Fig. 11.2), to the basic nodes of the grid

formed by intersections of the horizontal and vertical grid lines (solid squares in

Fig. 11.2). This was explained in detail in Chapter 7 (see Figs. 7.15, 7.17).

Steps 4–7: Solving the temperature equation

In order to avoid numerical diffusion of temperature we use the Lagrangian form

of heat conservation equation and advect the temperature with markers with the

technique described in Chapter 10. The temperature equation is formulated in 2D

for the case of variable thermal conductivity and takes into account heat generation

H from variable sources including radioactive (H

), adiabatic (H

), shear (H

)and

latent (H

) heat production:

ρC

=−

∂q

∂x

−

∂q

∂y

+ H

, (11.7)

where

=−k

∂T

∂x

=−k

∂T

∂y

= const,

= Tα



∂P

∂x

∂P

∂y



= σ



˙ε

+ σ



˙ε

+ σ

˙ε

+ σ

˙ε

= 2σ



˙ε

+ 2σ

˙ε

This equation takes into account the adiabatic heating term, which is in some

contradiction with using the incompressible ﬂuid approximation in the momentum

and continuity equations (Eqs. (11.1)–(11.3)). However, this is a common simpli-

ﬁcation (called the extended Boussinesq approximation) in numerical geodynamic

modelling. It is frequently adopted because of the very small thermal expansion

and compressibility of crustal and mantle rocks in the absence of phase transforma-

tions (Chapter 2). The calculation of H

can be simpliﬁed by neglecting deviations

(which are relatively small in most cases) of the dynamic pressure gradients

∂P

∂x