Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

Programming exercises and homework 177

volumetric changes which are of the form:

−

D ln ρ

= div(¯v) = 2sin(ψ)˙ε

II(plastic)

, (12.52)

˙ε

II(plastic)



˙ε



ij (plastic)

˙ε



ij (plastic)



1/2

, (12.53)

where ψ is the dilatation angle, which generally depends on total plastic strain, and

˙ε

II(plastic)

is the second invariant of the deviatoric plastic strain rate tensor.

Analytical exercise

Exercise 12.1

Derive the equation for visco-elastic stress build-up/relaxation with time, using the

Maxwell model (Eq. (12.40)) under conditions of constant strain rate ˙ε



, viscosity

η, shear modulus µ, and no stress rotation involved such that

D σ



Dσ



.Takethe

initial state of stress to be given by σ



0ij

and integrate Eq. (12.40) (now reformulated

in term of stress σ



) to obtain the analytical solution. Reformulate the resulting

equation in terms of Maxwell relaxation time

t

Maxwell

, (12.54)

which deﬁnes the characteristic time scale for visco-elastic stress relaxation.

Programming exercises and homework

Exercise 12.2

Use the analytical formula from the previous example to compute and compare

stress–time curves for the following parameters:

(1) σ



0ij

= 0Pa,˙ε



= 10

−14

1/s, η = 10

Pa s, µ = 10

Pa;

(2) σ



0ij

= 10

Pa, ˙ε



= 10

−14

1/s, η = 10

Pa s, µ = 10

Pa;

(3) σ



0ij

= 0Pa,˙ε



= 10

−15

1/s, η = 10

Pa s, µ = 10

Pa;

(4) σ



0ij

= 0Pa,˙ε



= 10

−14

1/s, η = 10

Pa s, µ = 10

Pa;

(5) σ



0ij

= 0Pa,˙ε



= 10

−14

1/s, η = 10

Pa s, µ = 10

Pa;

(6) σ



0ij

= 0Pa,˙ε



= 10

−14

1/s, η = 10

Pa s, µ = 10

Pa.

Try to understand how the different parameters control the stress build-up/

relaxation. An example is in Viscoelastic_stress.m.

178 Elasticity and plasticity

Exercise 12.3

Compute the visco-elasto-plastic stress build-up and observe the changes in the

viscous, elastic and plastic strain rates with time when using the parameters from

case (4) of the previous example. Assume the condition that the visco-elastic stress



must not exceed the yield stress limit of 1.5 ×10

Pa. Use Equation (12.46)

to compute the viscous strain rate. Use Equations (12.45), (12.47)and(12.48)to

compute elastic and plastic strain rates. Consider that after reaching the yielding

limit, the stress in the visco-elasto-plastic material should not change any more and

therefore

D σ



Dσ



= 0. An example is in Viscoelastoplastic_strain_rate.m.

Exercise 12.4

Modify Exercise 6.3 by adding Peierls creep for the high stress region (>10

Pa).

Compute the effective viscosity for this region by analogy to Eqs. (6.16)–(6.18) as

follows

eff

diff

disl

Peierls

, (12.55)

where η

Peierls

is Peierls creep viscosity deﬁned on the basis of Eqs. (12.44)and

(6.4) as

Peierls

exp



+ PV



1 −



Peierls







. (12.56)

Use the following Peierls creep parameters (Evans and Goetze, 1979; Katayama

and Karato, 2008): dry olivine – k = 1, q = 2, A

Peierls

= 10

−4.2

−2

−1

, E

540 000 J/mol, σ

Peierls

= 9.1 ×10

Pa; wet olivine – k = 1, q = 2, A

Peierls

−4.2

−2

−1

, σ

Peierls

= 2.9 ×10

Pa; E

= 430 000 J/mol. Note that the activa-

tion energy E

for Peierls creep is the same as for respective dislocation creep

(Table 6.1). Note that stress σ

used for computing effective viscosity with

Eq. (12.56) should always be limited by σ

Peierls

, which corresponds to the upper

strength limit. An example is in Peierls_creep.m.

2D implementation of

visco-elasto-plastic rheology

Theory: Numerical implementation of visco-elasto-plastic rheology.

Organisation of a thermomechanical code in case of 2D, visco-

elasto-plastic, multi-phase ﬂows.

Exercises: Programming a 2D thermomechanical code with a visco-

elasto-plastic rheology.

13.1 Viscous-like reformulation of visco-elasto-plasticity

One way of reformulating the visco-elasto-plastic rheological model (12.45) for

easy implementation into a viscous code (which we already have programmed)

is based on using ﬁnite differences in time. The deviatoric stress σ



is expressed

as a function of the total deviatoric strain rate ˙ε



from the visco-elasto-plastic

constitutive relationships (Eq. (12.45)), by using ﬁrst-order ﬁnite differences in

time to represent the objective co-rotational time derivatives

D σ



of visco-elastic

stresses

D σ



− σ

o

t

, (13.1)



= 2η

˙ε



Z + σ

o

(

1 − Z

)

, (13.2)

Z =

tµ

tµ + η

, (13.3)

= η when σ

<σ

yield

, and η

= η

ηχ + σ

, for σ

= σ

yield

, (13.4)

in which t is the computational time step, σ

o

indicates the deviatoric stress

from the previous time step corrected for advection and rotation, Z is the visco-

elasticity factor and η

is a viscosity-like Lagrangian parameter that characterises

the intensity of the plastic deformation (η

= η when no plastic yielding occurs).

179

180 2D implementation of visco-elasto-plastic rheology

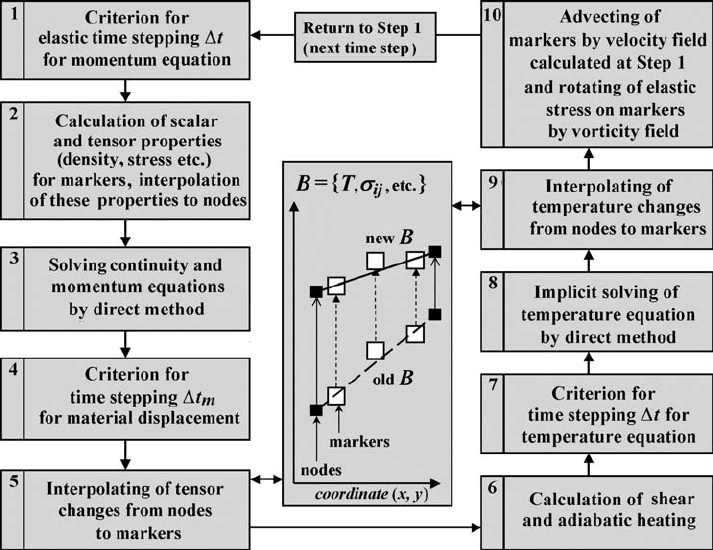
Fig. 13.1 Flow chart representing an example of a possible structure for a numer-

ical thermomechanical visco-elasto-plastic 2D code which uses ﬁnite-differences

and marker-in-cell technique (FD+MIC) for solving momentum, continuity and

temperature equation. (Gerya and Yuen, 2007).

Equation (13.2) can also be applied to a visco-elastic Maxwell rheology by using

the condition that η

= η.

13.2 Structure of visco-elasto-plastic thermomechanical code

When using the constitutive relationship (Eq. (13.2)) between the stress and strain

rate, we can now formulate the momentum, continuity and temperature equations

for the case of visco-elasto-plastic deformation in 2D and implement these equa-

tions in a thermomechanical visco-elasto-plastic modelling algorithm (Fig. 13.1).

The algorithm is largely based on our viscous thermomechanical code structure

discussed in Chapter 11 (Fig. 11.1, 11.2).

The ﬂow chart in Fig. 13.1 gives an example of a possible structure of a numer-

ical thermomechanical visco-elasto-plastic 2D code, which uses ﬁnite-differences

combined with a marker-in-cell technique (FD+MIC) to solve the momentum,

continuity and temperature equations. The principal steps of the algorithm are as

follows:

13.2 Structure of visco-elasto-plastic code 181

1. Deﬁning an optimal computational time step t for the momentum and continuity

equations. One can use a minimum time step value, which satisﬁes the following three

conditions: a given absolute time step limit on the order of a minimal characteristic

timescale for the processes being modelled; a given relative marker displacement step

limit (typically 0.01–1.0 of minimal grid step) that corresponds to the velocity ﬁeld

calculated at the previous time step (see Step 3); a given relative fraction of Lagrangian

markers reaching locally the yielding condition (Eq. (12.51)) for the ﬁrst time (typically

0.0001–0.01 of the total amount of markers representing materials with deﬁned plastic

yielding condition).

2. Calculating the physical properties (η

, µ, ρ, C

, k, etc.) for the markers and inter-

polating these newly calculated properties, as well as scalars and tensors deﬁned on

the markers (T, σ



, etc.) to the Eulerian nodes (Fig. 13.2). The plastic yielding con-

dition (Eq. (12.51)) is locally controlled on markers by using Eq. (13.2) to predict

stress changes. This equation is solved in an iterative way for every marker in order to

compute η

based on a local viscous ﬂow law (Eq. 6.5a) and a local plastic ﬂow rule

(Eq. 13.4).

3. Solving the 2D Stokes and continuity equations and computing the velocity and pressure

by solving the global matrix with a direct method.

4. Deﬁning an optimal displacement time step t

for markers (typically limiting the

maximal displacement to 0.01–1.0 of the minimal grid step) which can be generally

smaller or equal to the computational time step t (see Step 1).

5. Calculating the stress changes (Eq. (13.2)) on the Eulerian nodes for the displacement

step t

(see Step 4) and interpolating these changes to the markers and calculating

new tensor values associated with the markers (see central panel in Fig. 13.1).

6. Calculating the shear and adiabatic heating terms H

s(i,j)

and H

a(i,j)

at the Eulerian

nodes from the computed velocity, pressure, strain rate and stress ﬁelds (see Step 3).

7. Deﬁning an optimal time step t

for the temperature equation. One can use a minimum

time step value satisfying the following conditions: a given absolute time step limit on

the order of a minimal characteristic thermal diffusion timescale for the processes

being modelled; a given optimal marker displacement time step limit (see Step 3); a

given absolute nodal temperature change limit (typically 1–20 K) (Chapter 10). The

temperature equation can be preliminary solved with the displacement time step t

to deﬁne possible temperature changes.

8. Solving the temperature equation implicitly in time by a direct method. The temperature

equation can be solved in several steps when t

<t

9. Interpolating the calculated nodal temperature changes (see central panel in Fig. 13.1)

from the Eulerian nodes, to the markers, and calculating new marker temperatures.

10. Advecting all markers throughout the mesh according to the globally calculated velocity

ﬁeld (see Step 3). Components of the stress tensor deﬁned on the markers are recomputed

analytically to account for any local stress rotation.

Figure 13.2 shows the geometry of an irregularly spaced, fully staggered numer-

ical grid corresponding to the algorithm. The visco-elasto-plastic code can be

developed on the basis of viscous thermomechanical code (Chapter 11). Therefore,

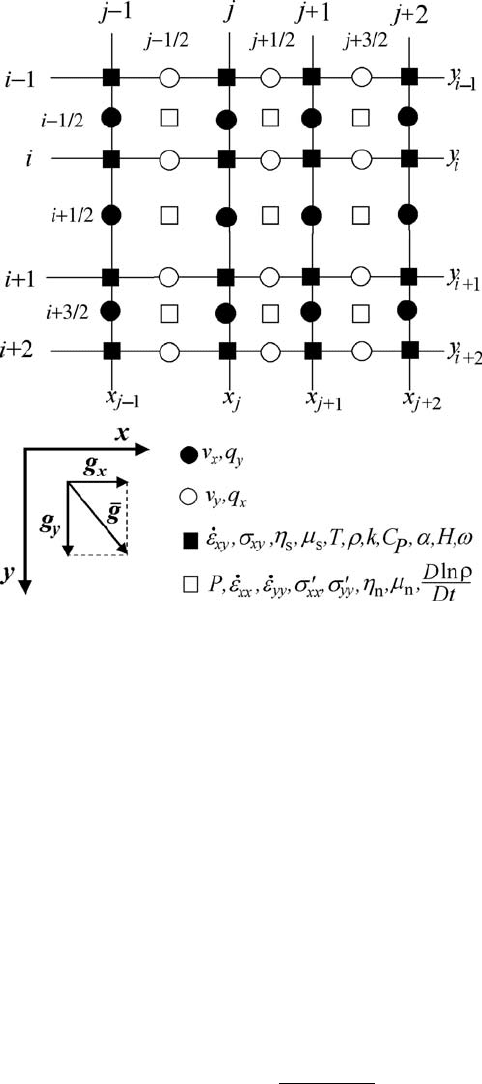
182 2D implementation of visco-elasto-plastic rheology

Fig. 13.2 Staggered 2D irregularly spaced numerical grid corresponding to the

algorithm presented in Fig. 13.1.

we will concentrate in the following sections on the new modiﬁcations that were

made to the code described in Chapter 11.

Step 1: Deﬁning an optimal computational time step

Note that the computational time step t, for the momentum and continuity equa-

tions and the displacement time step t

, for markers are generally independent

from each other and can only be related by the condition t

≤t. For an elas-

tic medium, the velocity ﬁeld numerically computed from the Stokes equation

strongly depends on the value of t. This time step inﬂuences the numerical

viscosity η

numerical

, which can be derived from Eqs. (13.2), (13.3)

numerical

= η

Z =

µt

+ µt

13.2 Structure of visco-elasto-plastic code 183

If t is much less then the Maxwell relaxation time

t

Maxwell

(13.5)

of a visco-elastic/visco-elasto-plastic medium, then this medium behaves purely

elastically, η

 µt and the numerical viscosity depends linearly on the time

step

numerical

= µt. (13.6)

In this situation, the smaller we take the time step, the smaller the computational

viscosity becomes which results in larger velocities. Clearly this causes numerical

problems, since if t tends to zero, the velocities will tend towards inﬁnity. Physi-

cally meaningful solutions can be obtained in two ways. The ﬁrst approach is to take

an extremely small time steps (on the order of seconds or less) and introduce inertial

forces into the system by using Navier–Stokes rather than the Stokes equations.

Numerical models in this case will only be able to address the seismic modes of

deformation, within a very limited period of time (hours, days), which is obviously

objectionable if we want to model geodynamic processes that last for millions and

even billions (as e.g. mantle convection) of years. The second approach (e.g. Kaus

and Becker, 2007) is (when possible) to choose t in such a manner that it will be

signiﬁcantly shorter than the Maxwell time of the rheologically strongest materials

that are present in the numerical experiment (e.g. a high-viscosity lithosphere), but

signiﬁcantly larger than the Maxwell time of any rheologically weak materials (e.g.

low-viscosity asthenosphere). In this case, the weak materials satisfy the condition

 µt and they will behave purely viscously in a broad range of t, such that

their numerical viscosity is independent of the time step

numerical

= η

, (13.7)

which will tend to stabilise the velocity ﬁeld computed inside the model. For real-

istic variations in viscosity 10

<η <10

and shear modulus 10

<µ<10

of solid rocks, this approach allows one to have geologically relevant computational

time steps on the order of 10

–10

years.

It should also be pointed out that the actual numerical viscosity contrast in

experiments with visco-elastic materials

min (η

vp(min)

,tµ

min

) ≤ η

numerical

≤ min (η

vp(max)

,tµ

max

), (13.8)

is typically reduced compared to purely viscous experiments

vp(min)

≤ η

numerical

≤ η

vp(max)

. (13.9)

This contrast can be further reduced by decreasing the computational time step

t. This actually makes the visco-elastic numerical experiments computationally

184 2D implementation of visco-elasto-plastic rheology

‘easier’ than the purely viscous ones. On the other hand, the visco-elastic numerical

solutions become equivalent to the viscous one if we choose very large computa-

tional time steps, which are bigger than the maximal Maxwell relaxation time (Eq.

13.5) estimated locally (e.g. on markers) within the model.

Step 2: Interpolation of scalar ﬁelds, vectors and tensor ﬁelds

According to our algorithmic approach, the temperature ﬁeld as well as components

of the σ



and ˙ε



tensors are represented by values assigned to the markers. The

effective values of all these parameters at the Eulerian nodal points are interpolated

from the markers at each time step. As in the viscous code, we favour local

interpolation schemes (within half grid distance) for some parameters: viscosity,

shear modulus and deviatoric stress components. In order to avoid non-physical

‘rigid boundary’ effects on interfaces between high-η-low-µ and low-η-high-µ

materials, one should use a harmonic average rather than arithmetic mean for the

shear modulus (see Eq. (8.18), Fig. 8.8 for notations)

(i,j)



m(i,j)



m(i,j)

. (13.10)

As in the viscous code, both the viscosity (η) and shear modulus (µ) are deﬁned at

different points (cf. open and solid squares in Fig. 13.2) when used for computing

the normal and shear components of the deviatoric stress tensor. The viscosity,

shear modulus and the respective stress and strain rate components for these nodal

points are interpolated from markers found around the nodes at a distance less than

half of the local Eulerian grid step (see dashed boundary in Fig. 8.8).

Step 3: Solving the momentum and continuity equations

In the case of 2D visco-elasto-plastic compressible ﬂuid, the solution of Stokes

equations (11.1) and (11.2) does not change. The only alteration concerns the

expressions for the deviatoric stresses and strain rates



= 2η

˙ε



Z + σ

o

(

1 − Z

)

=−σ



, (13.11)

= 2η

˙ε

Z + σ

(

1 − Z

)

= σ

, (13.12)

˙ε





∂v

∂x

−

∂v

∂y



=−˙ε



, (13.13)

˙ε



∂v

∂y

∂v

∂x



. (13.14)

13.2 Structure of visco-elasto-plastic code 185

The conservation of mass is approximated by a compressible time-dependent 2D

continuity equation

D ln ρ

∂v

∂x

∂v

∂y

= 0. (13.15)

The conservative FD representation of the momentum equations (Eqs. (11.4),

(11.5)) modiﬁed for a visco-elasto-plastic rheology with Equations (13.11)–(13.14)

is as follows (see Fig. 13.2 for the indexing of the grid points):

x-Stokes equation (11.4)



∂

∂x



2η ˙ε







i+1/2,j



∂

∂y

(2η ˙ε



i+1/2,j

− 2

i+1/2,j +1/2

− P

i+1/2,j −1/2

j+1

− x

j−1

=−



∂

∂x



o

(1 − Z)





i+1/2,j

−



∂

∂y



(1 − Z)





i+1/2,j

−

i,j

+ ρ

i+1,j

(13.16)



∂

∂x



2η ˙ε







i+1/2,j

= 4



η ˙ε





i+1/2,j +1/2

−



η ˙ε





i+1/2,j −1/2

j+1

− x

j−1



∂

∂x



o

(

1 − Z

)





i+1/2,j

= 2



o

(

1 − Z

)



i+1/2,j +1/2

−



o

(

1 − Z

)



i+1/2,j −1/2

j+1

− x

j−1



∂

∂y

(2η ˙ε



i+1/2,j

= 2

[η ˙ε

i+1,j

− [η ˙ε

i,j

i+1

− y



∂

∂z



(

1 − Z

)





i+1/2,j



(

1 − Z

)



i+1,j

−



(

1 − Z

)



i,j

i+1

− y



o

(

1 − Z

)



i+1/2,j +1/2

n(i+1/2,j +1/2)

(i+1/2,j +1/2)

tµ

(i+1/2,j +1/2)

+ η

(i+1/2,j +1/2)



(

1 − Z

)



(i,j)

s(i,j)

xy(i,j)

tµ

s(i,j)

+ η

s(i,j)



η ˙ε





i+1/2,j +1/2

tµ

n(i+1/2,j +1/2)

˙ε



xx(i+1/2,j +1/2)

tµ

n(i+1/2,j +1/2)

+ η

n(i+1/2,j +1/2)

[η ˙ε

(i,j)

tµ

s(i,j)

˙ε

xy(i,j)

tµ

s(i,j)

+ η

s(i,j)

˙ε



xx(i+1/2,j +1/2)

x (i+1/2,j+1)

−v

x (i+1/2,j)

2(x

j+1

− x

)

−

y (i+1,j+1/2)

−v

y (i,j +1/2)

2(y

i+1

− y

)

˙ε

xy(i,j)

x (i+1/2,j)

− v

x (i−1/2,j)

i+1

− y

i−1

y (i,j +1/2)

− v

y (i,j −1/2)

j+1

− x

j−1

186 2D implementation of visco-elasto-plastic rheology

where σ

and σ

o

are the deviatoric stress tensor components from the previ-

ous time step (corrected for advection and rotation), which are interpolated from

markers; t is the computational time step. Discretisation of the y-Stokes equation

(11.5) is analogous to Eq. (13.16) (derive as an exercise).

The time-dependent compressible continuity Eq. (13.15) is discretised as fol-

lows

x (i+1/2,j+1)

− v

x (i+1/2,j)

j+1

− x

y (i+1,j+1/2)

− v

y (i,j +1/2)

i+1

− y

=−



D ln ρ



i+1/2,j +1/2

(13.17)

where

D ln ρ

are substantive density changes (e.g. Eq. (12.52)) interpolated from

markers.

As in the viscous code, the global matrix is solved by a highly accurate, direct

method and the numbering of unknowns in this global matrix remains the same.

Step 5: Interpolation of stress changes from nodes to markers

After deﬁning the material displacement time step t

, the changes in the effective

stresses and new stress ﬁelds for the Eulerian nodes are calculated at the respective

nodal points according to Eq. (13.2)as

σ



xx(i+1/2,j +1/2)



2η

n(i+1/2,j +1/2)

˙ε



xx(i+1/2,j +1/2)

− σ

o

xx(i+1/2,j +1/2)



n(i+1/2,j +1/2)

t

n(i+1/2,j +1/2)

+ µ

n(i+1/2,j +1/2)

t

, (13.18)

σ

xy(i,j)



2η

s(i,j)

˙ε

xy(i,j)

− σ

xy(i,j)



s(i,j)

t

s(i,j)

+ µ

s(i,j)

t

, (13.19)



xx(i+1/2,j +1/2)

= σ

o

xx(i+1/2,j +1/2)

+ σ



xx(i+1/2,j +1/2)

, (13.20)

xy(i,j)

= σ

xy(i,j)

+ σ

xy(i,j)

. (13.21)

The corresponding stress increments for the markers are then added from the nodes

using a standard ﬁrst-order interpolation scheme (Fig. 8.9, Eq. (8.19)) and the

newly updated values of stress components σ



xx(m)

and σ

xy(m)

are thus obtained for

markers. Other stress components are not stored on markers since they are obtained

by using the standard relations σ



=−σ



and σ

= σ

The interpolation of the calculated stress component changes from the Eulerian

nodal points to the Lagrangian markers is similar to the temperature interpolation

strategy described in Chapter 10 and effectively reduces the problem of numerical

diffusion and non-physical subgrid oscillations. It uses a subgrid stress relaxation

operation occurring over a characteristic Maxwell time. In order to deﬁne this

operation, stress changes computed from Eqs. (13.18), (13.19) are decomposed into