Gerya T. Introduction to Numerical Geodynamic Modelling
Подождите немного. Документ загружается.

14.1 Multigrid – what is it? 197
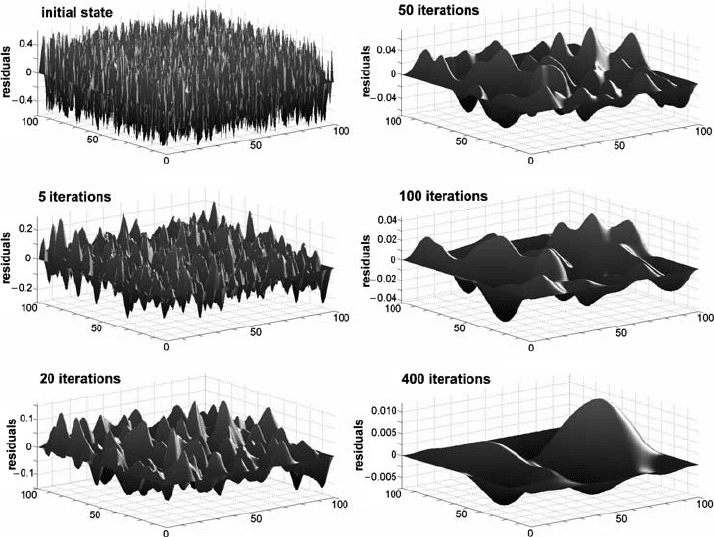
Fig. 14.2 Changes in the distribution of residuals during the iterative solution of 2D
Poisson equation for a model with initially random distribution of the density field.
Note that long-wavelength residuals decay much slower then short-wavelength
ones. The model is computed with the code Gauss_Seidel_iterations_Poisson.m
associated with this chapter. Model resolution is 100 ×100 grid points.
the corrections. To sum up: residuals and transport coefficients are interpolated
from finer to coarser levels (restriction operation) while computed corrections are
interpolated back from coarser to finer levels (prolongation operation). During one
iteration cycle, an accurate solution should only be obtained on the coarsest (last)
grid where many iterations or a direct matrix inversion can be employed (which can
be done at low computational costs since the resolution of this grid is small). On
other grids, some limited number of iterations (typically increasing by some factor
with increasing grid level) should be performed in order to propagate information
about the solution update and to compute new residuals. This process is called a
smoothing operation (the reason for using this term is obvious from Fig. 14.2).
It should be pointed out that an increase in the resolution by an integer factor
is not a strict requirement for multigrid. Generally, grid structures on different
levels could be made in a fully independent manner (e.g. by using independent
irregularly spaced meshes) and the only requirement is that coarser grids should
efficiently smooth residuals with larger wavelengths (Fig. 14.2). In this case, special
care should be taken when organising the restriction and prolongation operations
198 The multigrid method
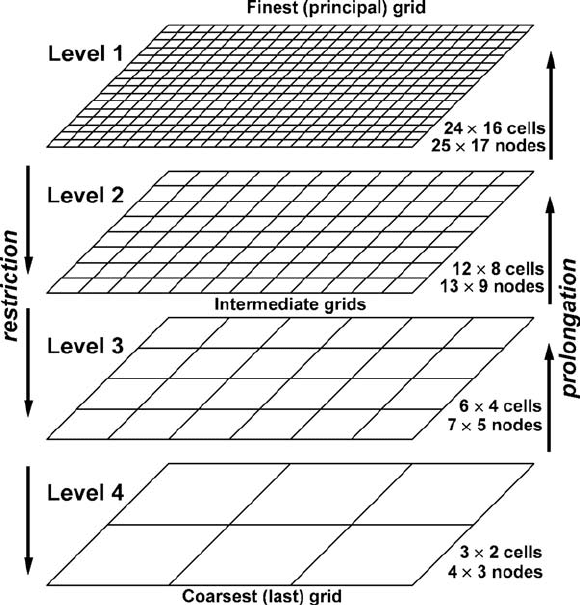
Fig. 14.3 Multigrid structure for a uniformly spaced, 2D rectangular non-staggered
grid with four levels of resolution. Resolution of the grid between two nearest levels
changes by the factor of 2 (see changes in the number of cells). Coarser levels
of resolution are responsible for the decay of larger residual wavelengths (see
Fig. 14.2).
between grids since the nodal points of the coarser grid do not overlap those
of the finer grid, even in the case of a regular rectangular non-staggered grid.
This situation is also very common for staggered grids (even in the case that
resolution increases by an even factor) – non-overlap of points between different
levels for a staggered grid is unavoidable and, therefore, the resolution at different
levels can be chosen quite independently. Indeed, the choice of grid resolution and
structure at various levels may notably affect the convergence of the solution. This
choice can thus be different for different numerical problems and can be optimised
empirically. Examples of programming such ‘arbitrary resolution multigrids’ for
the Poisson equation as well as for the momentum and continuity equations are
given respectively in the programs Poisson_Multigrid_planet_arbitrary.m and
Variable_viscosity_Multigrid_arbitrary.m associated with this chapter.
14.1 Multigrid – what is it? 199
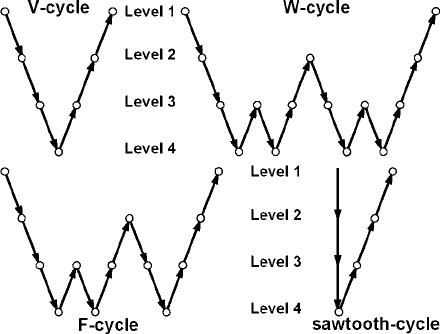
Fig. 14.4 Various multigrid schedules (or cycles) shown for the case of a four-
level multigrid algorithm (Fig. 14.3). Circles denote smoothing operation, arrows –
restriction (downward) and prolongation (upward) operations.
The order in which grids are visited is called the multigrid schedule or cycle.
Several standard schedules exist (Fig. 14.4): the V-cycle, the W-cycle, the F-cycle
and the sawtooth-cycle. The V-cycle is the simplest and most commonly used
multigrid schedule (Fig. 14.4) – restriction+smoothing go uniformly from the
finest level to the coarsest level through all intermediate levels, then prolongation+
smoothing go uniformly from the coarsest level to the finest level, also through
all intermediate levels. The order of operations for W- and F-cycles is more
complicated and contains several cycles of restriction+smoothing followed by
prolongation+smoothing between coarser levels (Fig. 14.4) before returning cor-
rections to the principal (finest) Level 1. The sawtooth-cycle is, in a way, similar to
the V-cycle but the smoothing operations are omitted during interpolation of resid-
uals from finer to coarser levels. Thus, this cycle first solves all equations on the
coarsest grid and then gradually ‘refines’ the solution toward the principal level by
applying prolongation+smoothing operations. The sawtooth-cycles are typically
applied when no good initial approximation of the solution exists on the principal
level, which is a common situation for the beginning of a numerical experiment.
Interpolation of residuals and transport coefficients from finer to coarser grid
(i.e. restriction operation) can be made in the same manner as the interpolation
of various parameters from markers to nodes (Eq. (8.18), Fig. 8.8). Consequently,
the interpolation of corrections from coarser to finer grid (i.e. prolongation
operation) can be organised by analogy with interpolation from nodes to mark-
ers (Eq. 8.19, Fig. 8.9). Since interpolation between markers and nodes was
already extensively discussed in Chapter 8, programming of restriction and
prolongation operations is rather straightforward, which is exemplified by several
200 The multigrid method
examples of written MATLAB functions (e.g. Poisson_restriction_planet,
Poisson_prolongation_planet, Viscosity_restriction, Stokes_Continuity_vis-
cous_restriction, Stokes_Continuity_prolongation) used in the codes associated
with this chapter. There are also more sophisticated schemes of organising
restriction and prolongation operations which give a higher multigrid performance
in specific cases (e.g. Wesseling, 1992).
It should also be mentioned that the method described in this chapter is called
geometrical multigrid, which requires the definition of several grids for the same
model, formulation of the same differential equations separately for each grid and
storing transport coefficients, solutions and corrections for all grids. Computational
and memory costs for the geometric multigrid are relatively small since coarser
grids have much less nodal points then the principal one. For example, in case of
grid coarsening by a factor of two, all coarser grids will have in 2D and 3D less
than 50% and 25% of grid points, respectively, compared to the finest grid.
However, there is also a class of more sophisticated multigrid approaches called
algebraic multigrid (AMG) which do not require the explicit definition of the
coarser grids, but rather uses algebraic operations based on multigrid principles to
process and solve global matrix constructed for the finest (principal) grid. In an
algebraic multigrid scheme, the coarse-level equations are generated from finer-
level equations without the use of any geometry or re-discretisation on the coarse
levels. This has the advantage that no coarse-level grid has to be generated or
stored, and no flux or source term needs be calculated on the coarse levels. This
feature makes AMG particularly important for use on unstructured meshes.
How efficient is multigrid? It is extremely efficient for simple cases like solv-
ing the Poisson equation on a regular grid (Fig. 14.2) and speeding up conver-
gence by several orders of magnitude (Fig. 14.5). In more complex, thermo-
mechanical modelling cases, it is typically less efficient, particularly when physical
phenomena (such as e.g. localisation of deformation) are not properly reproduced
on the coarser levels. For many geodynamic applications, the multigrid provides
one of the best options to build efficient and robust codes and is therefore widely
used in 3D numerical modelling of mantle convection and plate tectonic processes
(e.g., Tackley, 2000; 2008).
14.2 Solving the Poisson equation with multigrid
Implementation of a multigrid solver for the Poisson equation is generally quite
simple: a standard Gauss–Seidel iteration with a relatively high relaxation para-
meter θ
Poisson
relaxation
(up to 1.75 uniformly applied for all nodes in all grids) can be used
as an efficient smoother and the interpolation of residuals (restriction operation)
14.2 Solving the Poisson equation with multigrid 201
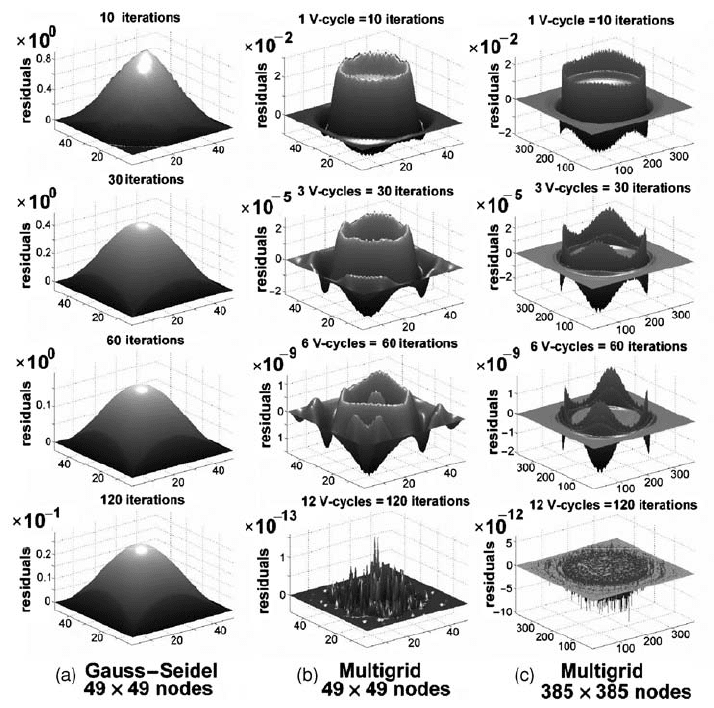
Fig. 14.5 Changes in the distribution of residuals during the iterative solution of
a 2D Poisson equation for a model with a density field that corresponds to a cir-
cular body (planet) embedded in a mass-less medium (space). (a) Gauss–Seidel
iterations at low grid resolutions. (b), (c) Multigrid iterations at both low (b) and
high (c) grid resolution, The multigrid cycle corresponds to a V-cycle with 5 +5
Gauss–Seidel iterations on the finest grid per cycle, four and seven levels of res-
olution are used for (b) and (c) respectively. Note that the convergence of the
numerical solution (decay of residuals) in case of multigrid is several orders of
magnitude faster (see bold numbers above vertical axes defining order of mag-
nitude for residuals) than for the same amount of simple Gauss–Seidel iterations
performed on the finest level. Also, in contrast to simple Gauss–Seidel iterations,
the convergence of the multigrid solutions is independent of grid resolution (com-
pare (b) and (c) with Fig. 14.1). The models are computed with the code Poisson_
Multigrid.m.
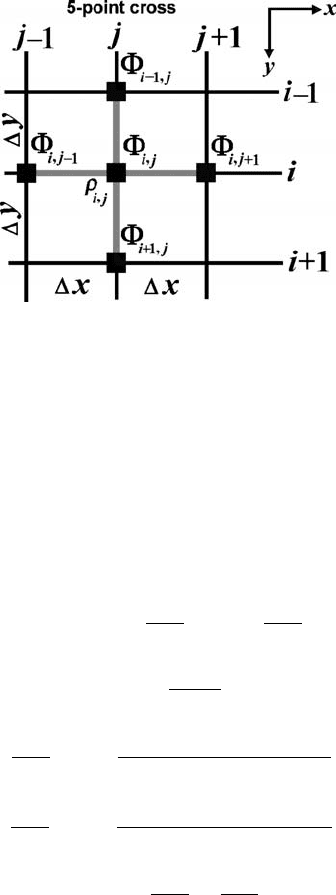
202 The multigrid method
Fig. 14.6 Stencil of the regular rectangular grid used for the discretisation of the
Poisson equation for the iterative Gauss–Seidel smoother used with multigrid.
and corrections (prolongation operation) is very straightforward particularly when
the resolution of a regular grid between adjacent levels increases by an integer
factor (2, 3 etc.) and grid lines of the coarser grid overlap with grid lines of the
finer grid (Fig. 14.3). A 5-point stencil in 2D for the discretisation of the Poisson
equation on such a regular grid is shown in Fig. 14.6 and the following iterative FD
representation is used for updating the solution with a Gauss–Seidel smoother
R
i,j
= R
i,j
−
∂
2
∂x
2
i,j
−
∂
2
∂y
2
i,j
, (14.6)
new
i,j
=
i,j
+
R
i,j
C
i,j
θ
Poisson
relaxation
, (14.7)
∂
2
∂x
2
i,j
=
i,j−1
− 2
i,j
+
i,j+1
x
2
, (14.8)
∂
2
∂y
2
i,j
=
i−1,j
− 2
i,j
+
i+1,j
y
2
, (14.9)
C
i,j
=−
2
x
2
−
2
y
2
, (14.10)
where
i,j−1
,
i−1,j
,
i,j
,
i+1,j
,
i,j+1
are the current values of either gravity
potential (at finest level) or corrections for this potential (at coarser levels) in
respective nodal points, C
i,j
is the coefficient at
i,j
in the discretised Poisson
equation, R
i,j
is the current residual and R
i,j
is the right-hand side of the Poisson
equation. On the principal level (finest grid), the right-hand side is computed from
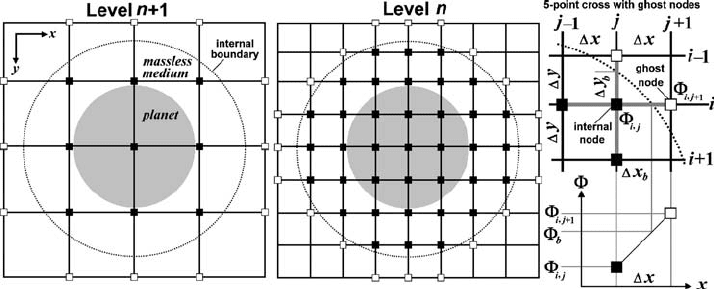
14.2 Solving the Poisson equation with multigrid 203
Fig. 14.7 Rectangular grids for two levels of resolution in case of solving Poisson
equation for 2D numerical model with an internal boundary based on multigrid.
Poisson equation is solved for internal nodes of the grids located inside the bound-
ary (solid squares). Ghost nodes (open squares) located immediately outside the
boundary are used to formulate internal boundary conditions when discretising
the Poisson equation for the nearest internal nodes.
the standard equation
R
i,j
= 4KπGρ
i,j
, (14.11)
where G is the gravitational constant and K depends on the geometry of self-
gravitating body modelled in 2D (K =1andK =2/3 stand for cylindrical and
spherical geometry, respectively, Eq. (11.16)). For coarser levels, R
i,j
is composed
of residuals interpolated from finer levels. Obviously, grid steps x and y are also
different for different levels of resolution. In a standard case, the simplest possible
boundary condition equation
i,j
=0 is used for all marginal nodes on all grids,
which also poses no difficulty for programming.
A peculiar case, occurs when an internal boundary is present within the model
on which a boundary condition to solve the Poisson equation has to be defined
(Fig. 14.7). This is, for example the case when we want to compute the gravity
potential inside and around a planet, which is a component of a spherical-Cartesian
approach for modelling self-gravitating bodies on a rectangular Cartesian grid
(Fig. 11.5). In order to force the planet to remain in the centre of the grid and obtain
a natural distribution of the gravitational acceleration vector inside the planet
(Chapter 11), a constant gravity potential boundary condition ( =
b
) in 2D can
be defined on a circle located at a distance from the planetary surface (Fig. 14.7).
In this case, the Poisson equation is solved only for the nodes located in the circle
(see solid squares in Fig. 14.7), while the boundary condition =
b
is applied
for all other nodes of the grid. In order to have consistent solutions for all levels

204 The multigrid method
of resolution, the FD representation of the Poisson equation should be modified
for the nodes located immediately next to the internal boundary with the use of a
ghost node approach. In this case, the derivative of the gravity potential on the side
of a 5-point cross which crosses the internal boundary should be defined in such
a manner that it satisfies the boundary condition =
b
. This situation is shown
in Fig. 14.7 (right part), where the horizontal derivative of gravity potential to the
right of the internal ij-th-node should satisfy the boundary condition =
b
and
the following FD equation can be formulated
∂
∂x
=
i,j+1
−
i,j
x
=
b
−
i,j
x
b
, (14.12)
where x is the horizontal grid step, x
b
is the distance from ij-th-node to the
circular boundary and
i, j+1
is the gravity potential for an imaginary (ghost) node
located at the distance x from ij-th-node. The value of gravity potential for the
ghost node can be then computed as
(i,j+1)
=
b
x
x
b
−
(i,j)
x − x
b
x
b
. (14.13)
Eq. 14.8 for the second x-derivative of gravity potential in Eq. 14.6 can be refor-
mulated to the form excluding
i, j+1
(verify as an exercise)
∂
2
∂x
2
i,j
=
i,j−1
1
x
2
−
i,j
x
b
+ x
x
2
x
b
+
b
xx
b
. (14.14)
A similar transformation can be done for Eq. 14.9 for the second y-derivative
of gravity potential for ij-th-node by using (i-1, j)-th-ghost-node (verify as an
exercise)
∂
2
∂y
2
i,j
=
i+1,j
1
y
2
−
i,j
y
b
+ y
y
2
y
b
+
b
yy
b
. (14.15)
Consequently, the coefficient C
i,j
in Eq. (14.7) will also change to
C
i,j
=−
x
b
+ x
x
2
x
b
−
y
b
+ y
y
2
y
b
. (14.16)
Ghost nodes are thus only used for reformulating the Poisson equation in the near-
est internal nodes and values of the gravity potential in the ghost nodes are not
computed explicitly. Moreover, the ‘implied’ gravity potential value (Eq. 14.13)
in a ghost node is generally different when the same ghost node is used in dif-
ferent Poisson equations formulated for different internal nodes. This is because
the gravity potential has a ‘kink’ on the circular boundary and it is taken to be
constant ( =
b
) for all nodes outside this boundary including all ghost nodes in
the final solution. However, the uniform use of Eqs. (14.14)–(14.16) to reformulate
14.3 Solving Stokes and continuity equations 205
the Poisson equation on different resolution levels is important and ensures the
geometrical compatibility of solutions between all multigrid levels. This is because
the boundary conditions for all grids are formulated on the same internal boundary,
irrespective of the resolution and actual positions of the nodal points relative to
this boundary. Note that the value of
b
should be set to zero for all levels of
resolution with the exception of the finest (principal) level since coarser levels are
used for computing corrections to the solution and these corrections should tend
to zero (and not to
b
) with an increasing number of iterations. An example of
a multigrid implementation with the circular internal boundary for gravity poten-
tial is given in the program Poisson_Multigrid_planet.m associated with this
chapter.
Solving the Poisson equation on an irregularly spaced grid is not very different
from the above procedures. Modifications only concern the manner of comput-
ing second derivatives of gravity potential in Eq. 14.6,theC
i,j
coefficient in
Eq. 14.7, and the way of finding a correspondence between nodal points of coarser
and finer grids when programming restriction and prolongation operations. The
necessary modifications of the Poisson equation can be made on the basis of
respective FD equations given in Chapter 11 (Fig. 11.4 Eq. (11.17)) while finding
a correspondence between nodal points is analogous to that between Lagrangian
markers (= nodes of finer grid) and Eulerian grid points (= nodes of coarser grid)
and can be based on the same bisection procedure presented in Chapter 8 (Fig.
8.8–8.10, Eqs. 8.18, 8.19).
14.3 Solving Stokes and continuity equations with multigrid
The main challenge for solving coupled momentum and continuity equations with
a multigrid method consists of programming a robust smoother that uses a prim-
itive variable (pressure–velocity) formulation. In the case of constant viscosity,
this challenge can be avoided by using a stream function formulation that requires
double solving of the Poisson equation (Chapter 5). However, we are more inter-
ested in creating a primitive variable smoother that allows explicitly computation
of pressure distribution in the model and is further applicable (with some modifica-
tions) to the variable viscosity case, which is much more relevant for geodynamic
applications. The main obstacle to building such a primitive variable smoother
comes from solving the incompressible continuity equation div(¯v) = 0 which does
not contain pressure and therefore (without modifications) cannot be converted into
a pressure solution update procedure as e.g. the Stokes equation (for velocity) or
Poisson equation (for gravity potential, see Eqs. 14.6, 14.7). This problem can be
overcome with the computational compressibility approach according to which an
iterative pressure update in a specific location is made proportional to the current

206 The multigrid method
residual of the continuity equation computed for the same location
R
continuity
i,j
= R
continuity
i,j
− div( ¯v)
i,j
, (14.17)
P
new
i,j
= P
i,j
+
R
continuity
i,j
β
computational
i,j
θ
continuity
relaxation
,
(14.18)
where R
continuity
i,j
is the right-hand side of the continuity equation (it is zero on the
finest level and is made of residuals for coarser levels), β
computational
i,j
is the com-
putational compressibility and θ
continuity
relaxation
is the relaxation coefficient used for the
continuity equation. Despite the artificial origin of this scheme for the incompress-
ible viscous medium, a surprisingly efficient choice of β
computational
i,j
can be made
for all levels of resolution on the basis of the simple relation:
β
computational
i,j
=
1
η
i,j
, (14.19)
where η
i,j
is the local viscosity. Equations (14.17)–(14.19) are applicable for
both variable and constant viscosity cases (in the constant viscosity case η
i,j
is
obviously equal to the global viscosity η for the entire model) and give stable
convergence of solutions for coupled momentum and continuity equations if the
relaxation coefficient θ
continuity
relaxation
is chosen to be 0.1–0.3. An explanation for this
surprising efficiency is that the computational compressibility provides a natural
way of coupling between pressure and velocity equations: in places where for the
current iteration step fluid converges and div( ¯v) < 0Eqs.(14.17)–(14.19) produce
an increase in pressure, thus creating an outward directed pressure gradient that
forces (through the Stokes equation) divergence of velocity and improves the
solution of the continuity equation; in places where fluid diverges and div( ¯v) > 0,
the reaction is opposite.
An efficient numerical representation of the momentum and continuity equations
for the multigrid can be based on a staggered grid with external velocity points
(Fig. 14.8), as discussed in Chapter 7 (Fig. 7.17). Since the global numbering of
unknowns is not needed in the case of iterative methods, the indexing of arrays
for different parameters can be done separately and these arrays will also have
different dimensions (Fig. 7.17): N
x
× N
y
for ρ and η
s
(viscosity used for shear
stress formulation) located in basic nodes, N
x
× (N
y
+ 1) for v
x
,(N
x
+1) ×N
y
for
v
y
and (N
x
−1) ×(N
y
−1) for P and η
n
(the viscosity used for normal deviatoric
stress components formulation), where N
x
and N
y
is respectively horizontal and
vertical resolution of the basic grid at a given multigrid level (see black rectangles
in Fig. 14.8).
