Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

15.2 3D staggered grid, discretisation of equations 227

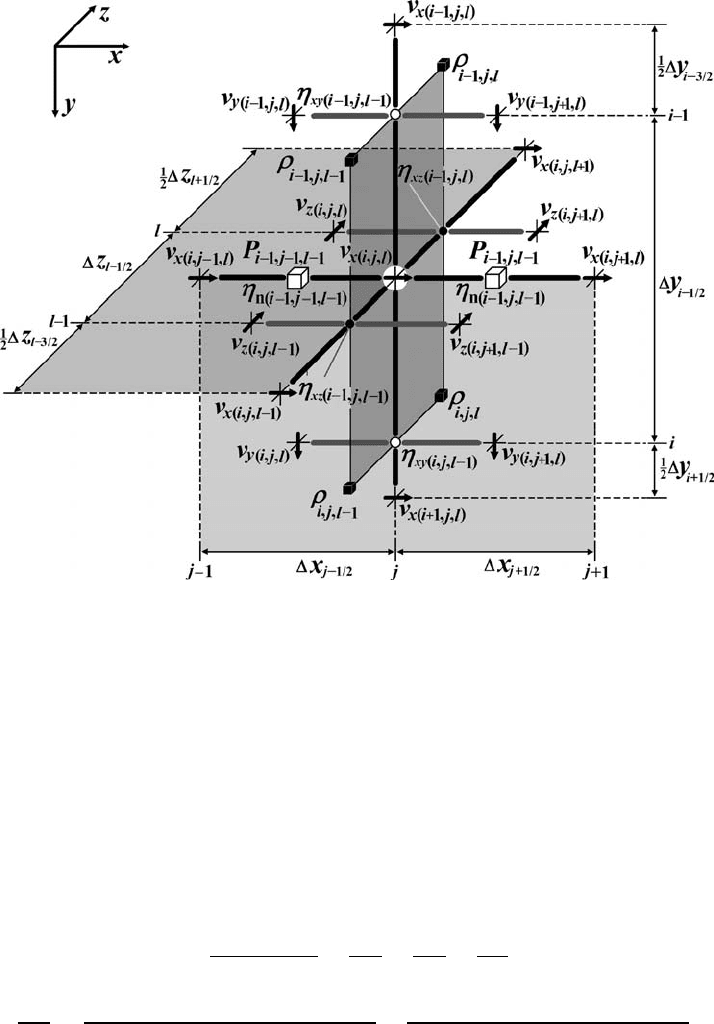
Fig. 15.5 Stencil of a 3D staggered grid used for the discretisation of the x-Stokes

equations with variable viscosity. The white circle in the centre corresponds

to a horizontal velocity node for which the x-Stokes equation is formulated.

The notation of different nodal points is as in Fig. 15.1. Indexing of different

variables corresponds to a 3D staggered grid with external velocity nodes

(Fig. 15.3).

Given that temperature advection is solved with markers (see Chapter 10),

discretisation of the 3D temperature equation with a variable thermal conductivity

can be done in a simple Lagrangian form, which does not include advective terms

and uses a stencil with 7 temperature nodes (7-point cross, Fig. 15.6). In implicit

form, the conservative FD can be written as follows

i,j,l

− T

i,j,l

t

∂q

∂x

∂q

∂y

∂q

∂z

= H

i,j,l

, (15.6)

∂q

∂x

i,j−1,l

+ k

i,j,l

)(T

i,j,l

− T

(i,j−1,l)

)

x

j−1/2

(x

j−1/2

+ x

j+1/2

)

−

i,j,l

+ k

i,j+1,l

)(T

i,j+1,l

− T

i,j,l

)

x

j+1/2

(x

j−1/2

+ x

j+1/2

)

(15.7)

228 Programming of 3D problems

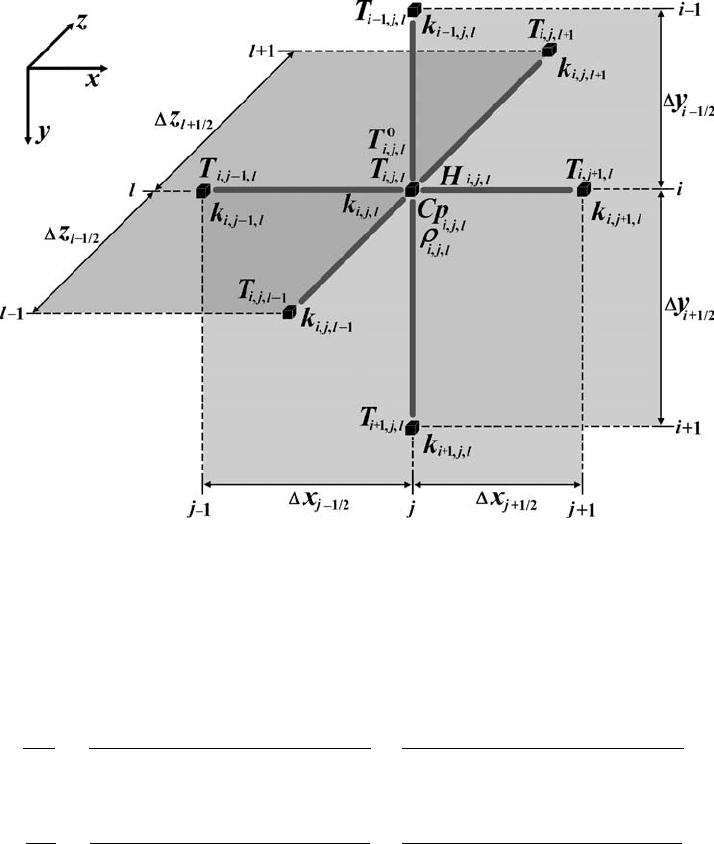
Fig. 15.6 Stencil of a 3D staggered grid used for discretisation of the temperature

equation with variable thermal conductivity. The temperature equation is formu-

lated for the central node T

i, j, l

which is one of the basic nodes of the 3D staggered

grid (Fig. 15.1). The notation of different nodal points is the same as in Fig. 15.1.

Indexing of different variables corresponds to a 3D staggered grid with external

velocity nodes (Fig. 15.3).

∂q

∂y

i−1,j,l

+ k

i,j,l

)(T

i,j,l

− T

i−1,j,l

)

y

i−1/2

(y

i−1/2

+ y

i+1/2

)

−

i,j,l

+ k

i+1,j,l

)(T

i+1,j,l

− T

i,j,l

)

y

i+1/2

(y

i−1/2

+ y

i+1/2

)

(15.8)

∂q

∂z

i,j,l−1

+ k

i,j,l

)(T

i,j,l

− T

i,j,l−1

)

z

l−1/2

(z

l−1/2

+ z

l+1/2

)

−

i,j,l

+ k

i,j,l+1

)(T

i,j,l+1

− T

i,j,l

)

z

l+1/2

(z

l−1/2

+ z

l+1/2

)

(15.9)

where T

i,j,l

is temperature for the current moment of time in the central ijl-th

node of the cross and T

i,j,l−1

, T

i,j,l+1

, etc. are temperatures in 7 nodal points

for the next moment of time, k

i,j,l−1

, k

i,j,l+1

, etc. stand for thermal conductivity

that can be different at different nodes, ρ

i,j,l

P i,j,l

, and H

i,j,l

is density, iso-

baric heat capacity and heat production values for the central node of the cross,

respectively.

15.2 3D staggered grid, discretisation of equations 229

Fig. 15.7 Stencil of a 3D staggered grid used for the discretisation of the Poisson

equation. The Poisson equation is formulated for the central node 

i,j,l

located

in one of the cell centres (pressure nodes) of the 3D staggered grid (Fig. 15.1).

The notation of different nodal points is the same as in Fig. 15.1. Indexing of

different variables corresponds to 3D staggered grid with external velocity nodes

(Fig. 15.3).

Like for the temperature equation, the discretisation of the Poisson equation in

3D is also based on a 7-point cross (Fig. 15.7)

∂



∂x

∂



∂y

∂



∂z

= πG(ρ

i,j,l

+ ρ

i+1,j,l

+ ρ

i,j+1,l

+ ρ

i+1,j +1,l

+ ρ

i,j,l+1

+ρ

i+1,j,l+1

+ ρ

i,j+1,l+1

+ ρ

i+1,j +1,l+1

)/2, (15.10)

∂



∂x

= 2



i,j+1,l

− 

i,j,l

x

j+1

(x

+ x

j+1

)

− 2



i,j,l

− 

i,j−1,l

x

(x

+ x

j+1

)

, (15.11)

∂



∂y

= 2



i+1,j,l)

− 

i,j,l

y

i+1

(

y

+ y

i+1

)

− 2



i,j,l

− 

i−1,j,l

y

(

y

+ y

i+1

)

, (15.12)

∂



∂z

= 2



i,j,l+1

− 

i,j,l

z

l+1

(

z

+ z

l+1

)

− 2



i,j,l

− 

i,j,l−1

z

(

z

+ z

l+1

)

. (15.13)

The density at the central node of the cross in Eq. (15.10) is computed as an

arithmetic average from 8 surrounding basic nodes. Alternatively, additional density

230 Programming of 3D problems

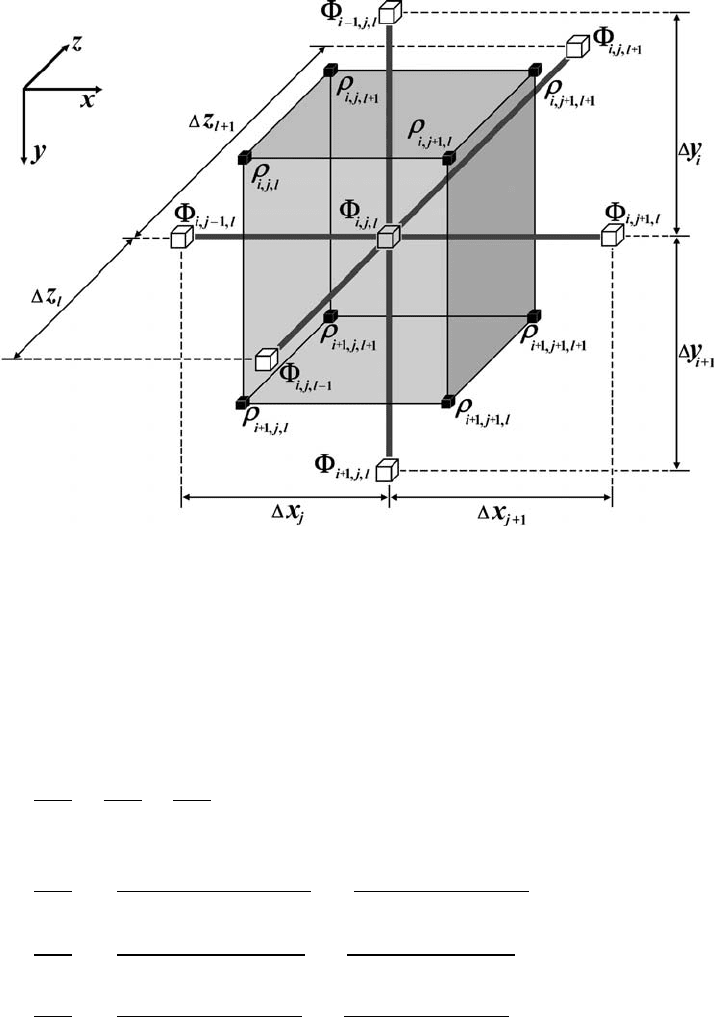
Fig. 15.8 Stencil of a 3D grid (8-nodes cell) used for the interpolation between

marker (grey cube) and nodes (black cubes).

points can be deﬁned in the same gravity potential nodes (i.e. in the centre of cells,

Fig. 15.1) and respective density values can be separately interpolated from markers

when deformation of self-gravitating body is modelled in 3D.

Finally, interpolation between markers and nodes in 3D is also based on the

same principles as those discussed for 2D interpolation in Chapter 8. It can be done

with the following standard ﬁrst-order of accuracy trilinear interpolation schemes

(Fig. 15.8): interpolation to ijl-th node from markers found in 8 cells surrounding

this node

(i,j,l)



m(i,j,l)



m(i,j,l)

, (15.14)

interpolation to a marker in a cell from 8 nodes surrounding the cell

= B

i,j,l

m(i,j,l)

+ B

i−1,j,l

m(i−1,j,l)

+ B

i,j−1,l

m(i,j−1,l)

i−1,j −1,l

m(i−1,j −1,l)

+ B

i,j,l−1

mi,j,l−1

+ B

i−1,j,l−1

mi−1,j,l−1

i,j−1,l−1

mi,j−1,l−1

+ B

i−1,j −1,l−1

mi−1,j −1,l−1

, (15.15)

where the statistical weight of m-th-marker for ijl-th-node depends on x

, y

z

distances to this nodes as

m(i,j,l)



1 −

x

j−1/2





1 −

y

i−1/2





1 −

z

l−1/2



. (15.16)

15.3 Solving discretised equations 231

15.3 Solving discretised 3D equations

After discussing discretisation of variable equations required for thermomechanical

geodynamic modelling in 3D, let us consider methods for solving these equations.

All approaches considered are iterative.

Temperature equation. Efﬁcient solving of the non-steady 3D temperature equa-

tion (15.6) does not require a multigrid since, in contrast to steady Stokes and Pois-

son equations, the time-dependent solutions for temperature are controlled locally

by local heat ﬂuxes rather than globally and can be implemented on the basis of a

Gauss–Seidel iteration with a relatively high relaxation parameter θ

temperature

relaxation

that

ranges from 0.5 to 1.5. The respective iterative temperature update scheme for a

regularly spaced grid based on Eqs. (15.6)−(15.9)isasfollows

new

i,j,l

= T

i,j,l

R

temperature

i,j,l

T (i,j,l)

temperature

relaxation

, (15.17)

R

temperature

i,j,l

= H

i,j,l

− ρ

i,j,l

P i,j,l

i,j,l

− T

i,j,l

t

−

∂q

∂x

−

∂q

∂y

−

∂q

∂z

(15.18)

∂q

∂x

i,j,l

+ k

i,j−1,l

)(T

i,j,l

− T

i,j−1,l

) − (k

i,j+1,l

+ k

i,j,l

)(T

i,j+1,l

− T

i,j,l

)

2x

(15.19)

∂q

∂y

i,j,l

+ k

i−1,j,l

)(T

i,j,l

− T

i−1,j,l

) − (k

i+1,j,l

+ k

i,j,l

)(T

i+1,j,l

− T

i,j,l

)

2y

(15.20)

∂q

∂z

i,j,l

+ k

i,j,l−1

)(T

i,j,l

− T

i,j,l−1

) − (k

i,j,l+1

+ k

i,j,l

)(T

i,j,l+1

− T

i,j,l

)

2z

(15.21)

T (i,j,l)

i,j,l

t

i,j−1,l

+ 2k

i,j,l

+ k

i,j+1,l

2x

i−1,j,l

+ 2k

i,j,l

+ k

i+1,j,l

2y

i,j,l−1

+ 2k

i,j,l

+ k

i,j,l+1

2z

, (15.22)

where x, y,andz are regular grid steps in respective directions, T

i,j,l

is the

temperature at the ijl-th node for the current moment of time, T

i,j,l

and T

new

i,j,l

are

old and new (updated) values of temperature at the ijl-th node for the next moment

of time. To satisfy the boundary condition equations, these equations are called for

marginal temperature nodes in the same Gauss–Seidel iteration cycle

upper boundary (i = 1)

no vertical heat ﬂux T

i=1,j,l

= T

i=2,j,l

constant temperature T

i=1,j,l

= T

top

232 Programming of 3D problems

left boundary (j = 1)

no horizontal heat ﬂux T

i,j=1,l

= T

i,j=2,l

constant temperature T

i,j=1,l

= T

left

front boundary (l = 1)

no lateral heat ﬂux T

i,j,l=1

= T

i,j,l=2

constant temperature T

i,j,l=1

= T

front

etc. for other boundaries. An example implementation of above algorithm is given

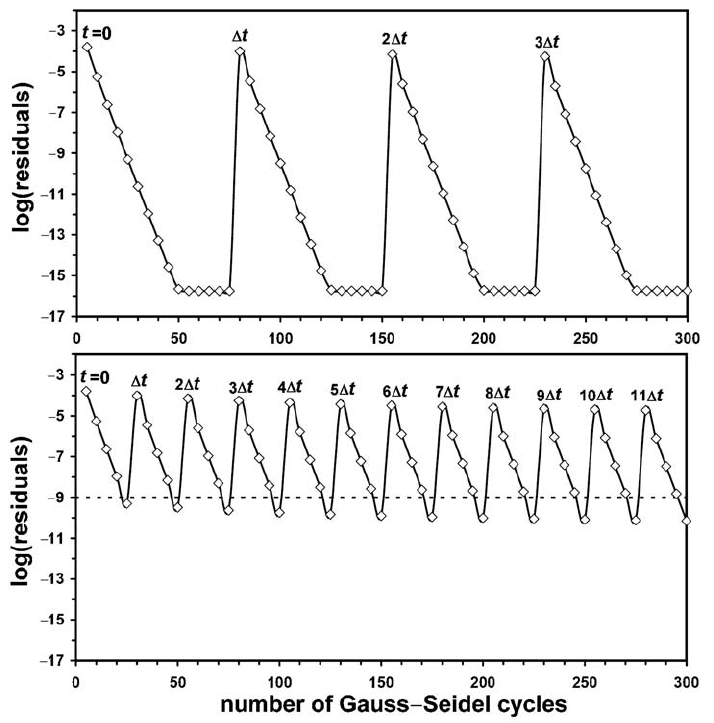
in the program Temperature3D_Gauss_Seidel.m. As can be seen from Fig. 15.9,

Gauss–Seidel iterations allow us to obtain high-accuracy solutions with 10–20

iterations per time step while the computer accuracy solution is obtained with a

few tens of iterations.

Poisson equation.Likein2D(Chapter 14), the efﬁcient solving of the 3D Pois-

son equation (15.10) can be based on a multigrid approach, that can again be

implemented on the basis of Gauss–Seidel iterations with a relatively high relax-

ation parameter θ

Poisson

relaxation

ranging from 0.5 to 1.5. The respective iterative gravity

potential update scheme for regularly spaced grid based on Eqs. (15.10)−(15.13)

is as follows



new

i,j,l

= 

i,j,l

R

i,j,l

(i,j,l)

Poisson

relaxation

, (15.23)

R

Poisson

i,j,l

= R

Poisson

i,j,l

−

∂



∂x

−

∂



∂y

−

∂



∂z

, (15.24)

∂



∂x



i,j−1,l

− 2

i,j,l

+ 

i,j+1,l

x

, (15.25)

∂



∂y



i−1,j,l

− 2

i,j,l

+ 

i+1,j,l

y

, (15.26)

∂



∂z



i,j,l−1

− 2

i,j,l

+ 

i,j,l+1

z

. (15.27)

(i,j,l)

=−

x

−

y

−

z

, (15.28)



i,j−1,l

,

i−1,j,l

, etc. are current values of either gravity potential (at ﬁnest level) or

corrections for this potential (at coarser levels) at respective nodal points, C

(i,j,l)

is the coefﬁcient at 

i,j,l

in the discretised Poisson equation, R

i,j,l

is the current

residual and R

i,j,l

is the right-hand side of the Poisson equation. On the ﬁnest

principal level of resolution, the right-hand side is computed from the standard

equation

i,j,l

= 4πGρ

i,j,l

, (15.29)

15.3 Solving discretised equations 233

(a)

(b)

Fig. 15.9 Decay of normalised residuals for the temperature equations with the

number of Gauss–Seidel cycles for a 3D model with variable thermal conductivity.

Residuals in (a) stabilise at computer accuracy level (10

−16

) after around 50

iterations (per time step). Iterations in (b) are terminated after reaching given level

of tolerance (10

−9

) that takes around 25 iterations per time step. Model resolution is

51 ×51 ×51 points with regularly spaced grid. Relaxation parameter θ

temperature

relaxation

1.25 is used (in Eq. 15.17). Numerical setup: rectangular block having higher

temperature is placed in lower temperature surrounding. Results are obtained with

program Temperature3D_Gauss_Seidel.m.

where G is the gravitational constant and ρ

i,j,l

the density deﬁned at the same

location as 

i,j,l

(alternatively use Eq. (15.10) when the gravity potential and

density are deﬁned at different points). For coarser levels, R

i,j,l

is composed of

residuals interpolated from ﬁner levels. Obviously, grid steps x, y and z are

different at different levels of resolution. Various boundary conditions are deﬁned

234 Programming of 3D problems

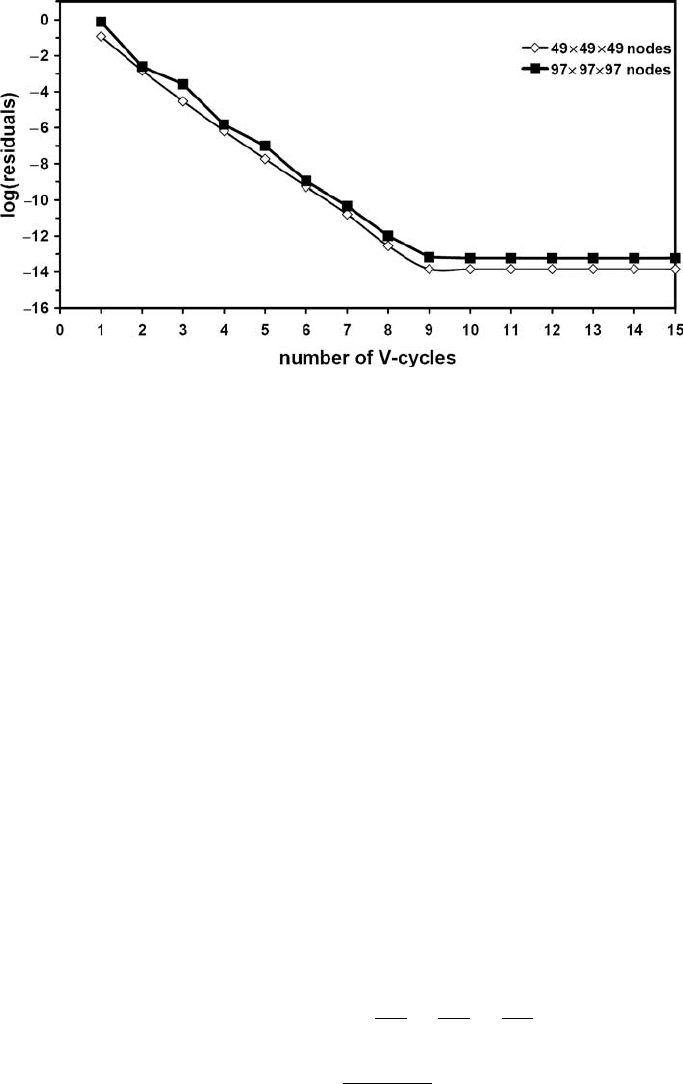
Fig. 15.10 Decay of normalised residuals for the 3D Poisson equation at various

resolutions versus number of multigrid V-cycles for a model with a spherical planet

embedded in a mass less medium (space). Residuals stabilise at computer accuracy

level. 5- and 6-level multigrid with resolutions respectively 49 ×49 ×49 (open

diamonds) and 97 × 97 ×97 (solid squares) nodes on the ﬁnest level are used

with a relaxation parameter θ

Poisson

relaxation

= 1.5. Results are obtained with program

Poisson3D_Multigrid_planet_arbitrary.m.

as in 2D (see Fig. 14.7,Eqs.(14.12)–(14.16)). An example implementation of

the above algorithm, for the case of a self-gravitating planet and gravity potential

boundary condition deﬁned on the internal spherical surface inside the grid is given

in the program Poisson3D_Multigrid_planet_arbitrary.m. As can be seen from

Fig. 15.10, multigrid allows us to obtain computer accuracy within around 10

V-cycles independent of the model resolution.

Momentum and continuity equations.Asin2D(Chapter 14), the efﬁcient solu-

tion of the 3D Stokes and continuity equations (15.1)−(15.5) can be based on a

multigrid approach that can be implemented on the basis of Gauss–Seidel iterations

with pressure updates computed from local divergence scaled to local viscosity. The

respective iterative pressure and velocity update schemes for a regularly spaced

grid can be derived on the basis of Eqs. (15.1)–(15.5)

new

i,j,l

= P

i,j,l

+ η

n(i,j,l)

R

continuity

i,j,l

continuity

relaxation

, (15.30)

R

continuity

i,j,l

= R

continuity

i,j,l

−

∂v

∂x

−

∂v

∂y

−

∂v

∂z

, (15.31)

new

x(i,j,l)

= v

x(i,j,l)

R

x-Stokes

i,j,l

(i,j,l)

Stokes

relaxation

, (15.32)

15.3 Solving discretised equations 235

new

y(i,j,l)

= v

y(i,j,l)

R

y-Stokes

i,j,l

(i,j,l)

Stokes

relaxation

, (15.33)

new

z(i,j,l)

= v

z(i,j,l)

R

z-Stokes

i,j,l

(i,j,l)

Stokes

relaxation

. (15.34)

For models with constant viscosity η, the respective residuals and coefﬁcients in

Eqs. (15.30)−(15.34) become

R

x-Stokes

i,j,l

= R

x-Stokes

i,j,l

− η



∂

∂x

∂

∂y

∂

∂z



∂P

∂x

, (15.35)

R

y-Stokes

i,j,l

= R

y-Stokes

i,j,l

− η



∂

∂x

∂

∂y

∂

∂z



∂P

∂y

, (15.36)

R

z-Stokes

i,j,l

= R

z-Stokes

i,j,l

− η



∂

∂x

∂

∂y

∂

∂z



∂P

∂z

, (15.37)

n(i,j,l)

= η, (15.38)

∂

∂x

x(i,j−1,l)

− 2v

x(i,j,l)

+ v

x(i,j+1,l)

x

, (Fig. 15.5) (15.39)

∂

∂y

x(i−1,j,l)

− 2v

x(i,j,l)

+ v

x(i+1,j,l)

y

, (Fig. 15.5) (15.40)

∂

∂z

x(i,j,l−1)

− 2v

x(i,j,l)

+ v

x(i,j,l+1)

z

, (Fig. 15.5) (15.41)

∂P

∂x

i−1,j,l−1

− P

i−1,j −1,l−1

x

, (Fig. 15.5) (15.42)

(i,j,l)

=−

2η

x

−

2η

y

−

2η

z

, (15.43)

and other terms can be derived in a similar manner (derive as an exercise).

For models with variable viscosity, the respective residuals and coefﬁcients in

Eqs. (15.32)–(15.34) become

R

x-Stokes

i,j,l

= R

x-Stokes

i,j,l

−

∂σ



∂x

−

∂σ

∂y

−

∂σ

∂z

∂P

∂x

, (15.44)

R

y-Stokes

i,j,l

= R

y-Stokes

i,j,l

−

∂σ



∂y

−

∂σ

∂x

−

∂σ

∂z

∂P

∂y

, (15.45)

R

z-Stokes

i,j,l

= R

z-Stokes

i,j,l

−

∂σ



∂z

−

∂σ

∂x

−

∂σ

∂y

∂P

∂z

, (15.46)

∂σ



∂x

= 2η

n(i−1,j,l−1)

x(i,j+1,l)

− v

x(i,j,l)

x

−2η

n(i−1,j −1,l−1)

x(i,j,l)

− v

x(i,j−1,l)

x

, (Fig. 15.5) (15.47)

236 Programming of 3D problems

∂σ

∂y

= η

xy(i,j,l−1)



x(i+1,j,l)

− v

x(i,j,l)

y

y(i,j+1,l)

− v

y(i,j,l)

yx



−η

xy(i−1,j,l−1)



x(i,j,l)

− v

x(i−1,j,l)

y

y(i−1,j +1,l)

− v

y(i−1,j,l)

yx



(Fig. 15.5) (15.48)

∂σ

∂z

= η

xz(i−1,j,l)



x(i,j,l+1)

− v

x(i,j,l)

z

z(i,j+1,l)

− v

z(i,j,l)

zx



−η

xz(i−1,j,l−1)



x(i,j,l)

− v

x(i,j,l−1)

z

z(i,j+1,l−1)

− v

z(i,j,l−1)

zx



(Fig. 15.5) (15.49)

(i,j,l)

=−2

n(i−1,j,l−1)

+ η

n(i−1,j −1,l−1)

x

−

xy(i,j,l−1)

+ η

xy(i−1,j,l−1)

y

−

xz(i−1,j,l)

+ η

xz(i−1,j,l−1)

z

, (15.50)

and other terms can be derived similarly (derive as an exercise).

The methodology of using a multigrid approach for 3D models is the same

as in 2D cases, with the single difference that trilinear (Eqs. (15.14)–(15.16))

and not bilinear interpolation schemes should be used to construct the restriction

and prolongation operations. Example implementations of the above algorithm

for the case of constant and variable viscosity are given respectively in the programs,

Stokes_Continuity3D_Multigrid.m, Variable_viscosity3D_Multigrid.m and

Variable_viscosity3D_MultiMultigrid.m associated with this chapter. As can

be seen from Figs. 15.11, 15.12, multigrid allows us to obtain high-accuracy 3D

mechanical solutions at various viscosity contrasts. In the case of large viscos-

ity contrasts, a computer accuracy solution can often be obtained with a ‘multi-

multigrid’ approach (Fig. 15.12) using repetitive cycles of gradual increase in a

computational viscosity contrast, as described in Chapter 14.

Elastic stress rotation. 3D numerical models including elasticity should take

into account the elastic stress rotation (Chapter 12). One possible way is to use the

general form of Jaumann stress rate (see Eqs. (12.29)–(12.36)), which allows us

to compute the rate of change caused by rotation for various stress components

˙σ



ij(Jaumann)

= σ



− ω



, (15.51)

where ˙σ

ij(Jaumann)

is rate of change for the σ



deviatoric stress components, repeated

index k indicates summation and ω

, ω

are components of the anti-symmetric

rotation rate tensor (Eq. (12.29)). Using Eq. (15.51) in 3D for e.g. σ



, the deviatoric

stress component gives (see Eq. (12.31))

˙σ



xx(Jaumann)

= 2σ

+ 2σ

. (15.52)