Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

15.3 Solving discretised equations 237

(a)

(b)

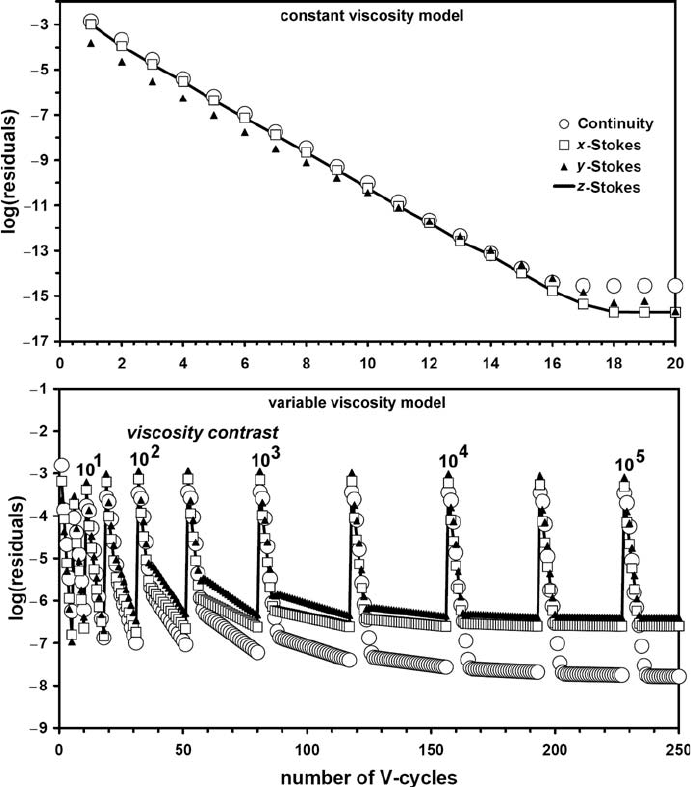
Fig. 15.11 Decay of normalised residuals for the Stokes and continuity equa-

tions versus number of multigrid V-cycles for 3D models with constant (a)

and variable (b) viscosity. A 5-level multigrid with resolution 49 ×49 ×49

nodes on the ﬁnest level is used with relaxation parameters θ

continuity

relaxation

= 0.3 and

Stokes

relaxation

= 0.9. Numerical setup: rectangular block having higher density (and

viscosity in (b) by factor 10

) sinks in lower density ﬂuid. Iterations start from

a hydrostatic pressure ﬁeld, zero velocities and no viscosity contrast. Resid-

uals in (a) stabilise at computer accuracy. Spikes in the solutions in (b) are

caused by an increase in viscosity contrast by the factor of 3.333 after reaching

given level of tolerance (10

−6

) for the sum of residuals. Results are obtained

with the programs Stokes_Continuity3D_Multigrid.m (a) and Variable_

viscosity3D_Multigrid.m (b).

238 Programming of 3D problems

(a)

(b)

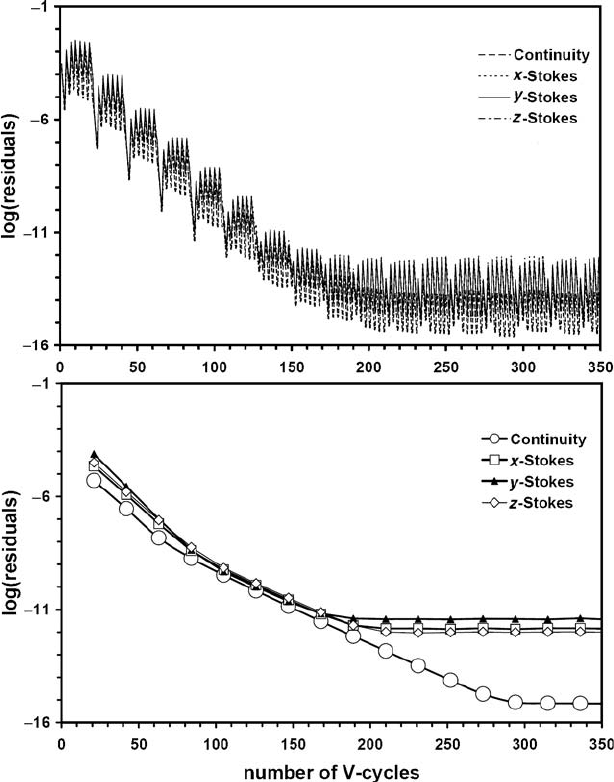
Fig. 15.12 Decay of normalised residuals for the Stokes and continuity equations

with the number of multigrid V-cycles for a 3D model with variable viscosity

in the case of a ‘multi-multigrid’ approach using repetitive cycles of gradual

increase in computational viscosity contrast. Residuals stabilise at computer accu-

racy level. 5-level multigrid with resolution 49 ×49 ×49 points on the ﬁnest level

is used with relaxation parameters θ

continuity

relaxation

= 0.75 and θ

Stokes

relaxation

= 1.25. Numer-

ical setup: rectangular block having higher density and viscosity (by factor 10

)

which sinks in ﬂuid with lower density and viscosity. Iterations start from a hydro-

static pressure ﬁeld and zero velocities. (a) Decay of local residuals computed

with current corrections and right-hand side within each cycle (steps) of gradual

viscosity contrast increase (spikes). (b) Decay of global residuals computed after

each cycle of gradual viscosity contrast increase. Spikes in (a) are caused by an

increase in viscosity contrast by the factor of 10 every 3 multigrid cycles. Results

are obtained with the program Variable_viscosity3D_MultiMultigrid.m.

Programming exercises and homework 239

Similar derivations can be made for other stress components (see Eqs. (12.32)–

(12.36)). Like in 2D models (Chapter 13,Eqs.(13.35)–(13.36)), the numerical

implementation of stress rotation is done by re-computing elastic stress components

stored at markers according to the ﬁrst-order accurate scheme



ij(rotated)

= σ



ij(m)

+ t

× ˙σ



ij(Jaumann)

= σ



ij(m)

+ t

(σ



− ω



), (15.53)

where σ



ij(m)

is the deviatoric stress component for a given marker, t

is the

marker displacement time step (Chapter 13)andω

the rotation rate components

that are deﬁned at the same nodal points and computed with similar FD schemes

as respective ˙ε



∂v

∂x

∂v

∂x



strain rate components (see Figs. 15.1, 15.3)

and then interpolated to markers using standard interpolation formula (Eq. (15.15),

Fig. 15.8).

Numerical algorithms. Numerical algorithms for the thermomechanical codes

in 3D, do not differ from algorithms described in Chapters 11, 13 for 2D codes with

the exception that direct solvers for various equations should rather be substituted

by the iterative ones described above.

Programming exercises and homework

Exercise 15.1

Program solving the 3D temperature equation on a regular 51 ×51 ×51 grid based

on Gauss–Seidel iteration (Eqs. (15.17)–(15.22)). The model setup corresponds

to hot rectangular block (20 ×20 ×20 km, T = 1500 K, ρ = 3100 kg/m

, C

1500 J/K/kg, k =1 W/m/K) which is located in a colder medium (T =1000 K, ρ =

3000 kg/m

, C

= 1000 J/K/kg, k = 3 W/m/K). The block is located in the

middle of the model, which is 100 ×100 ×100 km in size. Boundary conditions

are insulating at all boundaries. Use the relaxation parameter θ

temperature

relaxation

= 1.25 in

Eq. (15.17). An example is in Temperature3D_Gauss_Seidel.m.

Exercise 15.2

Generalise Exercise 14.1 to 3D. Solve the Poisson equation for the case of a

spherical planetary body embedded in a mass less-like medium (Eqs. (15.23)–

(15.29), Fig. 14.7). The number of resolution levels = 4, the resolution on the

coarsest (last) grid =7 ×7 ×7 nodal points, and the factor of increase in resolution

between the levels = 2. All other model parameters and material properties are

the same as in the 2D exercise. Use a ghost node approach along the spherical

boundary surface for the gravity potential in the same way as in 2D (Fig. 14.7,

Eqs. (14.13)–(14.16)), i.e. independently in x, y and z directions. An example is in

Poisson3D_Multigrid_planet_arbitrary.m.

240 Programming of 3D problems

Exercise 15.3

Generalise Exercises 14.2 and 14.3 to 3D. Solve the Stokes and continuity equations

for both constant and variable viscosity cases using a pressure–velocity formulation

and ghost node approach (Eqs. (15.30)–(15.50), Figs. 15.1–15.5). Model parame-

ters:modelsize= 100 ×100 ×100 km, block size = 20 ×20 ×20 km. Material

properties are the same as in 2D cases. Boundary conditions =free slip at all bound-

aries, number of resolution levels = 4, resolution of the basic grid on the coarsest

(last) level = 4 ×4 ×4 nodal points, factor of increase in resolution between the

levels = 2, relaxation coefﬁcients for Gauss–Seidel iterations θ

Stokes

relaxation

=0.9 and

continuity

relaxation

=0.3, number of smoothing iterations on the ﬁnest (basic) level = 5,

factor of increase in the number of iterations with the level coarsening = 2. For

the variable viscosity case, use a gradual increase in the viscosity contrast by a

factor 10

1/2

(Eq. (14.57)), to reach an accurate solution (Fig. 15.11). Examples are

in Stokes_Continuity3D_Multigrid.m and Variable_viscosity3D_Multigrid.m.

Numerical benchmarks

Theory: Numerical benchmarks: testing of numerical codes for various

problems. Examples of thermomechanical benchmarks.

Exercises: Programming of models for various numerical benchmarks.

16.1 Code benchmarking: why should we spend time on it?

Benchmarking of a numerical code means comparing the numerical solution

obtained with solving the system of linear equations with (i) analytical solutions

(ii) results of physical (analogue) experiments (iii) numerical results from other

(well-established) codes and (iv) general physical considerations. Benchmarking

of newly created numerical tools is sometimes very tedious, but an absolutely nec-

essary stage of code development as its purpose is to test the code’s robustness

in a broad range of situations relevant to geodynamic modelling applications. For

instance, if you plan to model with your code shear heating processes in deforming

rocks – make sure that your code provides the correct temperature changes related to

mechanical energy dissipation; if you model subduction – make sure that your code

handles correctly large viscosity contrasts and has no notable numerical diffusion

of the temperature ﬁeld and composition; if you intend to model self-gravitating

planetary bodies – make sure that your code computes correct gravity ﬁeld etc. We

should not be lazy and limit ourselves to one or two common benchmarks, such as

the Rayleigh–Taylor instability and convection with constant viscosity hoping that

everything else will work automatically. No, it will not! Therefore, test your code

on a broad range of challenging cases (several of which are discussed below), to

explore its limitations and be creative in inventing and calibrating new numerical

benchmarks. Then, in the end, you will be really proud of your ‘numerical child’.

Many of the analytical solutions that can be used for testing of thermomechanical

241

242 Numerical benchmarks

codes for geodynamically relevant situations can be taken from the textbook of

Turcotte and Schubert (2002), which we will also use for constraining some of our

numerical benchmarks.

Below we discuss details of several important benchmarks which test various

aspects of thermomechanical codes. These calibrating tests aim to verify the efﬁcacy

of numerical solutions for a variety of circumstances relevant to geodynamics.

These will include:

(a) sharply discontinuous viscosity distribution (test 1 and 2);

(b) strain rate dependent viscosity (test 3);

(d) shear heating for temperature dependent viscosity (test 5);

(e) advection of a sharp temperature front (test 6);

(f) heat conduction for temperature-dependent thermal conductivity (test 7);

(g) thermal convection with constant and variable viscosity (tests 8);

(h) elastic stress build-up and advection (test 9 and 10);

(i) localisation of visco-elasto-plastic deformation (test 11).

Of course this list is incomplete and many additional benchmarks exist, or can

be invented. Yet, performing the discussed benchmarks, we will at least get some

conﬁdence that we created a state-of-the-art numerical geodynamic modelling tool

which correctly reproduces a number of challenging geodynamic models.

16.2 Test 1. Rayleigh–Taylor instability benchmark

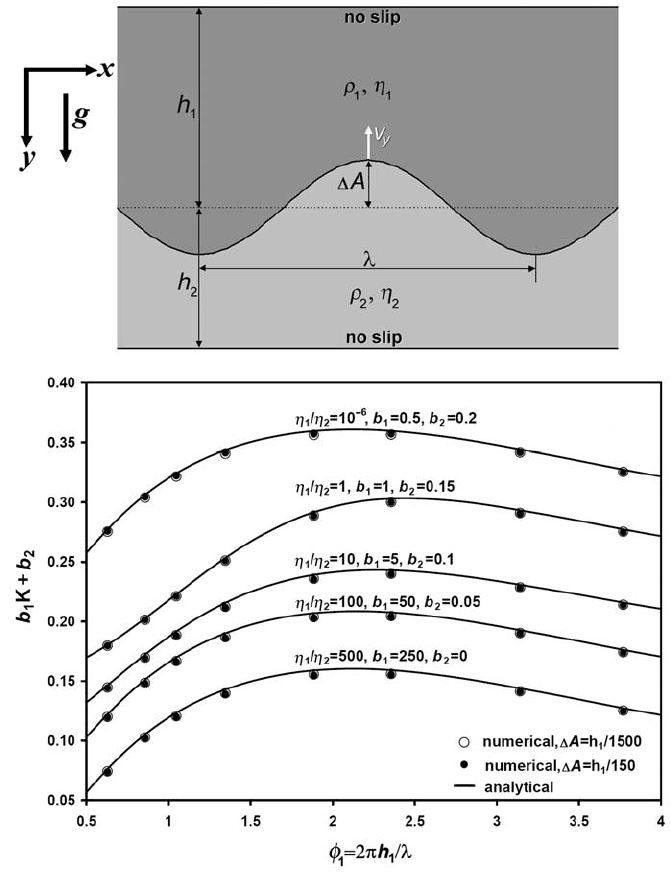
This is a typical analytical solution based benchmark. To test correctness of the

numerical velocity solution for gravity driven ﬂows, in the case of sharply het-

erogeneous density and viscosity ﬁelds, one can use a two-layer Rayleigh–Taylor

instability model (e.g. Ramberg, 1968) with a no-slip condition on the top and at the

bottom and symmetry conditions along the vertical walls (Fig. 16.1(a)). An initial

sinusoidal disturbance of the boundary between the upper (η

, ρ

)andthelower

(η

, ρ

) layers of thicknesses h

and h

, respectively, has a small initial amplitude

(A) and a wavelength (λ). Under this condition, the velocity of the diapiric growth

) is given by the relation (Ramberg, 1968)

A

=−K

− ρ

2η

K =

−d

− d

(16.1)

2φ



cosh 2φ

− 1 −2φ



−

2φ

cosh 2φ

− 1 −2φ

(

sinh 2φ

− 2φ

)



cosh 2φ

− 1 −2φ



sinh 2φ

− 2φ

cosh 2φ

− 1 −2φ

16.2 Test 1. Rayleigh–Taylor instability benchmark 243

(a)

(b)

Fig. 16.1 Rayleigh–Taylor instability benchmark. (a) Initial setup. (b) Compari-

son of numerical (symbols) and analytical (lines, Eq. (16.1)) solutions for the case

of two layers with equal thicknesses (h

). Arbitrary scaling coefﬁcients b

and

are used in (b) for plotting results computed at variable viscosity contrasts on

the same diagram. Growth factor K for numerical cases is computed from velocity

ﬁeld based on Eq. (16.1). Numerical results are calculated at resolution 51 ×51

nodes and 250 ×250 markers with the code Variable_viscosity_Ramberg.m.

244 Numerical benchmarks

(

sinh 2φ

+ 2φ

)



cosh 2φ

− 1 −2φ



(

sinh 2φ

+ 2φ

)

cosh 2φ

− 1 −2φ

2φ



cosh 2φ

− 1 −2φ



−

2φ

cosh 2φ

− 1 −2φ

2πh

where K is a dimensionless growth factor.

With a marker-in-cell method, a small layer boundary perturbation (less than

one grid step) can easily be prescribed on a sub-grid scale by small sinusoidal

(vertical) displacements of markers that are initially distributed regularly inside the

numerical grid

A

= cos



2π

− 0.5L



A, (16.2)

where x

and A

are horizontal coordinate and vertical displacement for a given

marker m and L is the horizontal width of the numerical model. For proper con-

straining the numerical models, the relationship L =2λ can be used together with

free slip (i.e. horizontal symmetry) conditions on two vertical boundaries.

Figure (16.1(b)) compares numerical and analytical solutions for the growth

rate of the instability estimated for two layers of equal thickness of (i.e. h

)

at different values of A, λ and η

/η

. Good accuracy at large variations of the

disturbance wavelength and layer viscosity contrasts (η

/η

=10

−6

–5 ×10

) sug-

gests that the tested numerical code is capable of correctly modelling the velocity

ﬁelds for gravity driven ﬂows across a boundary with sharp changes in density

and viscosity. Even very small perturbations of the horizontal boundary are prop-

erly captured by variations in relative position of markers via a bilinear density

interpolation procedure from markers to nodes. An example of the numerical setup

for conducting the Rayleigh–Taylor instability benchmark is given by the code

Variable_viscosity_Ramberg.m.

16.3 Test 2. Falling block benchmark

This is a typical example of a benchmark which is based on general physical

considerations. I personally like it very much, since it is simple to implement

but creates challenging conditions to be handled numerically. In the case of an

isolated rigid object, sinking in a low viscosity surrounding, the velocity of the

object mainly depends on the viscosity of its surrounding (weakest medium). As

16.3 Test 2. Falling block benchmark 245

Fig. 16.2 Initial conditions (top left) and results of the numerical experiments for

the falling block benchmark performed by Gerya and Yuen (2003a). Boundary

conditions: free slip at all boundaries. Black and white dots represent positions of

markers for the block and the medium, respectively. Grid resolution of the model

is 51 ×51 nodes, 22 500 markers.

was discussed in Chapter 14, this situation differs from modelling the Rayleigh–

Taylor instability where the strong layer is attached to the model boundaries and

the velocity ﬁeld is deﬁned by the strongest medium. According to our physical

intuition, (i) deformation of the block should vanish with increasing viscosity

contrast (Fig. 16.2) and (ii) the sinking velocity at high viscosity contrasts should

246 Numerical benchmarks

Fig. 16.3 Velocity of the rectangular block sinking in a viscous medium as a

function of viscosity contrast between the block and the background medium.

The model setup corresponds to Fig. 16.2. (top left). Numerical results are cal-

culated at a resolution of 51 ×51 nodes and 250 ×250 markers with the code

Variable_viscosity_block.m.

be independent of the absolute value of the viscosity of the block but should

solely depend on that of the surrounding medium (Fig. 16.3). In the case of using

ﬁnite differences for solving the momentum equations, they should be formulated

in a stress-conserving way (see Chapter 7). This test also proves the accurate

conservation properties of a numerical procedure in terms of preserving the block

edges geometry (Fig. 16.2) at large deformation and high (10

–10

) viscosity

contrast between the stiffer block and the weak surroundings. An example of the

numerical setup for conducting the falling block benchmark is given by the code

Variable_viscosity_block.m.

16.4 Test 3. Channel ﬂow with a non-Newtonian rheology

This test can be conducted to check the numerical solution of the momentum and

continuity equations for ﬂows with a strongly strain-rate/stress-dependent rheology,

which is characteristic of dislocation creep (Ranalli, 1995). The computation is

carried out for vertical ﬂow of a non-Newtonian (with a power-law index n) viscous

medium in a section of an inﬁnite vertical channel (Fig. 5.2) of width L in the

absence of gravity. Boundary conditions are taken as follows: a given constant