Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

10.2 Conservative ﬁnite differences 137

and 3 is given by

node 2:



∂q

∂x



= 2

− q

(x

+ x

)



∂q

∂x



=−

(

− T

)

/x

− k

− T

)/x

(x

+ x

)/2

, (10.8a)

node 3:



∂q

∂x



= 2

− q

(x

+ x

)



∂q

∂x



=−

(

− T

)

/x

− k

− T

)/x

(x

+ x

)/2

, (10.8b)

which imply that the expressions for heat ﬂux q

at nodes 2 and 3 are identical:

=−k

− T

x

Thus, a conservative FD formulation of the temperature equation (either explicit

or implicit) is based on the following three formal rules that are analogous

to the rules discussed in Chapter 7 for the Stokes equation with variable

viscosity.

(1) The temperature equation is initially discretised in term of heat ﬂuxes at basic nodes

of the grid (cf. nodes 2, 3, Fig. 10.4),

node 2:



ρC



= 2

− q

(x

+ x

)

node 3:



ρC



= 2

− q

(x

+ x

)

(2) These heat ﬂuxes are formulated for additional (heat ﬂux) nodes of the grid (cf. nodes

A, B, C, Fig. 10.4)

node A: q

=−k

− T

x

node B: q

=−k

− T

x

node C: q

=−k

− T

x

Note that we have to use thermal conductivity values k

, k

and k

for the additional

nodes (A, B, C) at the locations where the heat ﬂuxes are deﬁned. If these values are

not known, they can be computed by e.g. arithmetic averaging of known thermal

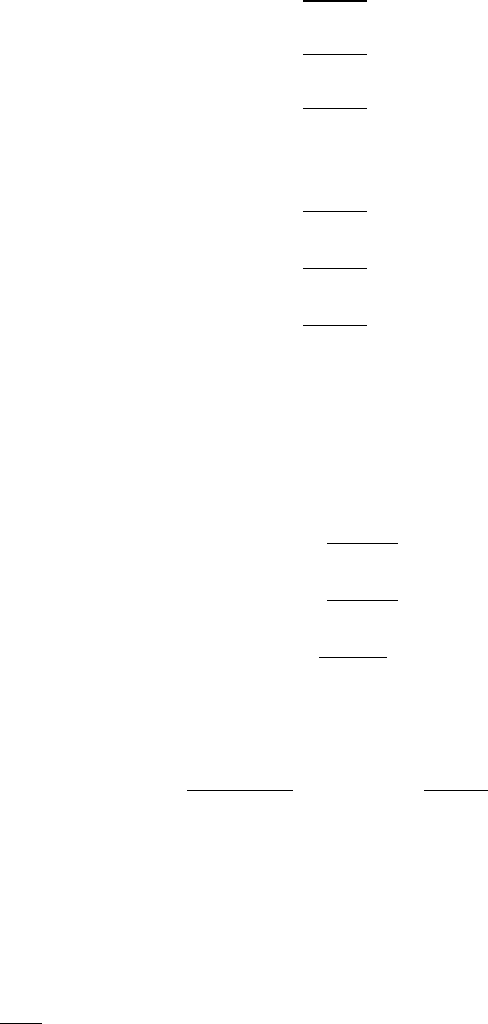
138 Numerical solution of the heat conservation equation

conductivity values from the basic nodes (1, 2, 3, 4)

+ k

Another possibility is to use harmonic averaging

+ k

The harmonic average formula can be derived from the condition that the heat ﬂux

to the left of the additional nodes must equal the ﬂux to the right of these nodes. The

derivation for node B is done under the assumption that the thermal conductivities

between nodes 2 and B, and between B and 3 remain constant, and are equal to k

and k

, respectively. Then the following equation can be formulated,

=−2k

− T

x

=−2k

− T

x

=−k

− T

x

Solving these equations with respect to T

and k

gives (please verify as an

exercise)

+ T

+ k

and k

+ k

Derivations for nodes A and C can be done similarly (please verify as an exercise).

(3) Identical formulations of heat ﬂuxes are used for the temperature equation at different

basic nodes.

It is important to mention that conservative ﬁnite differences are formulated

in terms of the thermal conductivity (k) and not in terms of the thermal diffusivity

κ =

ρC

, otherwise one can obtain artiﬁcial variations in heat ﬂuxes due to spatial

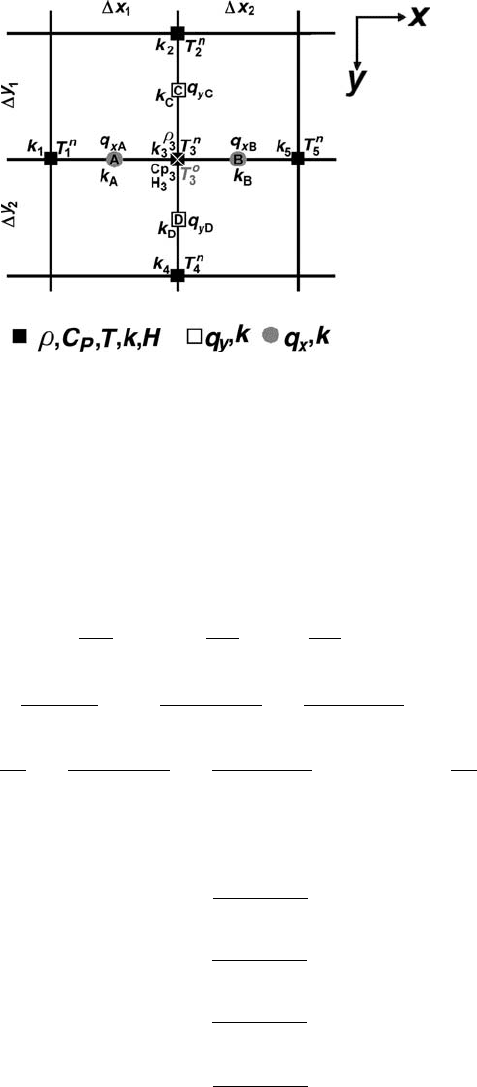
10.2 Conservative ﬁnite differences 139

Fig. 10.5 Stencil of a 2D grid used for the implicit discretisation of the Lagrangian

temperature equation with variable thermal conductivity. The crossed square

corresponds to the node for which the temperature equation is formulated.

variations in density (ρ) and/or heat capacity (C

). Both density and heat capacity

should always be taken from the basic node on which this equation is formulated.

By applying these rules in 2D, the following conservative implicit FD formula-

tion can be derived for the Lagrangian temperature equation (Fig. 10.5)





=−



∂q

∂x



−



∂q

∂y



+ H

, (10.9a)

− T

t

=−2

− q

x

+ x

− 2

− q

y

+ y

+ H

, (10.9b)

t

+ 2

− q

x

+ x

+ 2

− q

y

+ y

= H

+ ρ

t

, (10.9c)

where

=−k



− T



x

=−k



− T



x

=−k



− T



y

=−k



− T



y

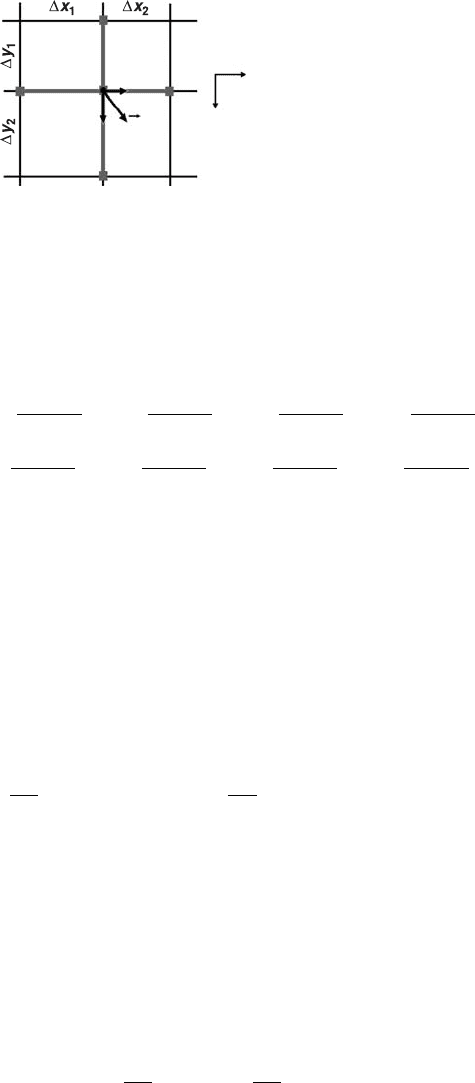
140 Numerical solution of the heat conservation equation

x 3

Fig. 10.6 Stencil of a 2D grid used for the explicit discretisation of the advective

term for the Eulerian temperature equation.

If values of thermal conductivity for heat ﬂux nodes (A, B, C, D) are not known,

they can be computed by averaging known thermal conductivity values from the

basic nodes (cf. black squares in Fig. 10.5). For example,

arithmetic average: k

+ k

;

harmonic average: k

+ k

Obviously, conservative 2D formulations can also be explicit (derive as an

exercise).

10.3 Advection of temperature with Eulerian methods

If the temperature equation is solved in an Eulerian form for a deforming/moving

medium, then the advective term v · grad(T ) is present in the temperature

equation

ρC



∂T

∂t

+v · grad(T )



=−

∂q

∂x

+ H. (10.10)

where i is a coordinate index and x

is a spatial coordinate, and it should be

included in the FD formulation. When discretising this term, explicit ﬁnite dif-

ferences are typically used, based on temperature and velocity at the current time

instant. A common approach is to use asymmetric ‘upwind’ differences (Chapter 8),

i.e. to perform the differencing against the direction of material ﬂow vector

(Fig. 10.6)

¯v

· grad(T )

= v



∂T

∂x



+ v



∂T

∂y



. (10.11)

10.4 Advection of temperature with markers 141

Explicit upwind differences are then as follows

¯v

· grad(T )

= v



∂T

∂x



+ v



∂T

∂y



, (10.11a)



∂T

∂x



− T

x

when v

> 0and



∂T

∂x



− T

x

when v

< 0,

(10.11b)



∂T

∂y



− T

y

when v

> 0and



∂T

∂y



− T

y

when v

< 0.

(10.11c)

Such explicit advection terms are simply added to the right-hand side of the tem-

perature equation (10.9).

It should be mentioned that advective terms can also be formulated implic-

itly. Indeed, irrespective of the formulation these terms always introduce artiﬁcial

numerical diffusion of temperature on the Eulerian grid (Chapter 8). This problem

is not relevant for slow ﬂow because real physical diffusion is typically faster than

numerical diffusion and the latter can be neglected. Numerical diffusion, however,

becomes relevant for models with rapid advection (e.g. in subduction models). This

problem can be minimised by: (i) using more complicated, higher-order Eulerian

advection FD schemes (Chapter 8) and (ii) advecting temperature with Lagrangian

points (method of characteristics, method of markers) which will be discussed

below. Including advective terms in the temperature equations imposes an addi-

tional restriction on the time step given by the Courant criteria (Eq. 8.5).

10.4 Advection of temperature with markers

In order to avoid numerical diffusion of temperature one can use the Lagrangian

form of heat conservation equation (Chapter 9) and advect temperature with the

marker-in-cell technique described in Chapter 8. The temperature equation is then

formulated in a Lagrangian form

ρC

=−

∂q

∂x

+ H, (10.12)

and is discretised with Eq. (10.9).

After solving the Lagrangian temperature equation on the Eulerian nodes

(Fig. 10.5) the changes in the effective temperature ﬁeld for the Eulerian nodes are

calculated as

T

i,j

= T

t+t

i,j

− T

i,j

. (10.13)

142 Numerical solution of the heat conservation equation

(a)

(b)

Fig. 10.7 Temperature structure of the markers for a zoomed-in area of the numer-

ical model of convection (Gerya and Yuen, 2003a). Different colours of markers

correspond to different values of temperature assigned to the markers. T

and T

are the maximal and minimal temperatures for the experiment. (a) and (b) show

the results calculated without (d = 0) and with (d = 1) subgrid diffusion (see

Eq. 10.16), respectively.

The corresponding temperature increments for the markers T

, are then interpo-

lated from the nodes using relation 8.20 (Fig. 8.9) in order to calculate new marker

temperatures T

t+t

= T

+ T

. (10.14)

The interpolation of the calculated temperature changes from the Eulerian nodal

points, to the Lagrangian markers reduces numerical diffusion in an efﬁcient man-

ner (Chapter 8). This method does not produce any smoothing of the temperature

distribution between adjacent markers (Fig. 8.11), thus resolving the thermal struc-

ture of a numerical model in much ﬁner details.

However, a main problem with treating advection-diffusion processes using the

simple incremental update scheme of Eq. (10.14) is that small-scale variations of

the thermal structures may appear on a subgrid scale (i.e. differences in tempera-

ture between closely located markers). These variations cannot be damped out by

the grid-scale corrections of Eq. (10.14). For example, in the case of strong chaotic

mixing of markers (e.g. due to thermal convection), Eq. (10.14) may produce

numerical oscillations of thermal ﬁeld assigned to the adjacent markers (Fig. 10.7a).

10.4 Advection of temperature with markers 143

These oscillations do not damp out with time based on a characteristic heat dif-

fusion timescale as would be the case if physical diffusion was active. The intro-

duction of a consistent subgrid diffusion operation is the way around this. In

order to deﬁne this operation, we decompose temperature changes computed from

Eq. 10.13 into a subgrid part T

subgrid

i,j

and a remaining part T

remaining

i,j

such

that

T

i,j

= T

subgrid

i,j

+ T

remaining

i,j

. (10.15)

In order to compute the subgrid part, we apply subgrid diffusion on the markers over

a characteristic local heat diffusion timescale t

diff

(Fig. 9.2) and then interpolate

the respective temperature changes back to nodes. Subgrid temperature changes on

markers are then computed as follows

T

subgrid



m(nodes)

− T





1 − exp



−d

t

diff



(10.16)

t

diff

(2/x

+ 2/y

)

where t

diff

is deﬁned for the corresponding cell of the grid where the marker is

located (Fig. 8.9); d is a dimensionless numerical diffusion coefﬁcient (one can

use empirical values in the range of 0 ≤ d ≤ 1). T

m(nodes)

, C

, ρ

and k

are

interpolated for a given marker, respectively, from T

i,j

, C

P(i,j)

, ρ

(i,j)

and k

(i,j)

values

for nodes using the relation (8.19) (Fig. 8.9).

After obtaining T

subgrid

for all markers T

subgrid

i,j

are computed by interpolation

from markers to nodes using Eq. (8.18) (Fig. 8.8)

T

subgrid

i,j



T

subgrid

m(i,j)



m(i,j)

(10.17)

where

m(i,j)



1 −

x





1 −

y



Then T

remaining

i,j

is computed for the nodes from Eq. (10.15)

T

remaining

i,j

= T

i,j

− T

subgrid

i,j

. (10.18)

Finally, the new corrected marker temperatures T

t+t

corrected)

are computed according

to the modiﬁed relation (10.14) that now takes into account Equations (10.15)–

(10.18) and thus removes the non-physical subgrid oscillations

t+t

m(corrected)

= T

+ T

subgrid

+ T

remaining

(10.19)

144 Numerical solution of the heat conservation equation

where T

subgrid

is given by Eq. (10.16)andT

remaining

is interpolated from

nodal values of T

remaining

i,j

to markers according to standard bilinear interpolation

(Eq. (8.19), Fig. 8.9).

Equation (10.16) requires the decay of differences between marker temperature

values T

and interpolated nodal temperature values T

m(nodes)

on the characteristic

timescale (t

diff

) of local heat diffusion. It is important to emphasise that the subgrid

diffusion does not change the total temperature increments T

i,j

computed on nodal

points from the heat conservation equation. Instead it splits them into two parts

T

subgrid

i,j

and T

remaining

i,j

. By introducing a subgrid diffusion operation, unrealistic

subgrid oscillations are removed (see Fig. 10.7(b)) over the characteristic local

heat diffusion timescale without affecting the accuracy of numerical solution of

the temperature equation. Realistic subgrid oscillations will, however, be preserved

by this scheme if they are related, for example, to the rapid mixing by advection

dominating ﬂows.

It is also important to mention that subgrid diffusion is a method for correcting

small non-physical subgrid oscillations that appear on the markers due to mechani-

cal mixing processes. It is not the way to remove any arbitrary discrepancy between

the marker and nodal temperature ﬁelds. Such discrepancies can appear, for exam-

ple, due to prescribing sharp temperature fronts on a ﬁne marker grid which cannot

be properly resolved by a coarse nodal grid. Big initial temperature discrepancies

between markers and nodes should always be eliminated by re-interpolation of the

initial nodal temperatures (with applied boundary conditions) back to markers with

the use of Eq. (8.19) before making the ﬁrst time step.

10.5 Thermal boundary conditions

In order to solve the temperature equation numerically, thermal boundary con-

ditions have to be speciﬁed. These conditions depend on the type of numer-

ical problem. The following boundary conditions are frequently used in geo-

modelling:

(1) constant temperature

(2) insulating boundary (zero heat ﬂux, symmetry condition)

(3) constant heat ﬂux

(4) inﬁnity-like conditions (external constant temperature)

(5) periodic boundary

(6) combined boundary conditions

Numerical examples of different boundary conditions are shown below

(Fig. 10.8).

10.5 Thermal boundary conditions 145

∆x

Fig. 10.8 Stencil of a 2D grid used for the discretisation of the thermal boundary

conditions.

(1) A constant temperature condition implies that the temperature at a boundary is assigned

a given value (which may change both along the boundary and in time)

T = const (x,y, z, t) (10.20a)

or in discretised form (Fig. 10.8)

= const (x, y,z,t) (10.20b)

This condition is typically applied at the lower and upper boundaries of geodynamic

models.

(2) An insulating boundary condition (no heat ﬂux, lateral symmetry condition) means

that heat does not ﬂux through a boundary which implies (from Eq. (9.1)) that no

temperature gradient exists across this boundary, i.e.

=−k

∂T

∂x

∂T

∂x

= 0, (10.21a)

or in discretised form (Fig. 10.8)

− T

= 0. (10.21b)

The symmetry condition is used at the lateral boundaries for almost every 2D and 3D

Cartesian geodynamic model.

(3) A constant heat ﬂux condition does not limit the temperature values at a boundary, but

prescribes a heat ﬂux across the boundary (this heat ﬂux can be time and coordinate

dependent)

=−k

∂T

∂x

= const(x, y, z, t), (10.22a)

or in discretised form (Fig. 10.8)

− T

x

= const(x, y, z, t). (10.22b)

(4) Inﬁnity-like conditions either mimic the absence of a thermal boundary or imply that

this boundary is located very far away. For example, the external constant temperature

condition (Burg and Gerya, 2005; Gerya et al., 2008b) implies that condition (10.20a)

146 Numerical solution of the heat conservation equation

and (10.20b) are satisﬁed at a parallel boundary located at the distance L from the

actual boundary of the model, and that the temperature gradient between these two

boundaries is constant

∂T

∂x

T − T

external

L

, (10.23a)

or in discretised form (Fig. 10.8)

− T

x

− T

external

L

, (10.23b)

− T

L

L +x

x

L +x

external

. (10.23c)

where T

external

= const (x, y, z,t) is the prescribed temperature at the parallel external

boundary.

(5) Periodic boundary conditions are typically established for paired parallel lateral bound-

aries of a model and imply that temperature ﬁelds at both sides of each boundary are

identical. The physical meaning and usage of this condition is the same as for the

respective mechanical boundary condition (Chapter 7).

(6) Combined conditions represent a mixture of several types of boundary conditions.

Thermal boundary conditions can also be applied inside the model.

Programming exercises and homework

Exercise 10.1

Write a program to solve the temperature equation in 2D, in both explicit and

implicit form (Figs. 10.1 and 10.3, respectively). Use a regular grid of 51 ×31

points. The model size is 1000 × 1500 km (i.e. 1 000 000 × 1 500 000 m). Use

constant thermal conductivity k =3 W/m/K, density ρ = 3200 kg/m

and heat

capacity C

= 1000 J/kg/K for the entire model. Test Eq. (10.4) for the time step

limitation in the case when explicit FD are used. The initial setup corresponds to

background temperature of 1000 K with a rectangular thermal wave (1300 K) in

the middle (‘wave’ means perturbation of the temperature ﬁeld). Global indexing

of the unknowns in the implicit case is the same as for the 2D Poisson equation

(Exercise 3.2)

k = N

× (j − 1) + i, (10.24)

where k is the index in the global matrix computed from horizontal (j) and vertical

(i) geometrical indices and N

is the number of nodes in the vertical direction.

Try using constant temperature (1000 K, Eq. (10.20)), and insulating bound-

ary conditions (Eq. (10.21)) at all boundaries. An example is in Explicit_

Implicit2D.m.