Gerya T. Introduction to Numerical Geodynamic Modelling

Подождите немного. Документ загружается.

8.2 Eulerian advection methods 107

upwind

central

downwind

i 1

i+1

(a)

(b)

(c)

x x

i +1

+ t

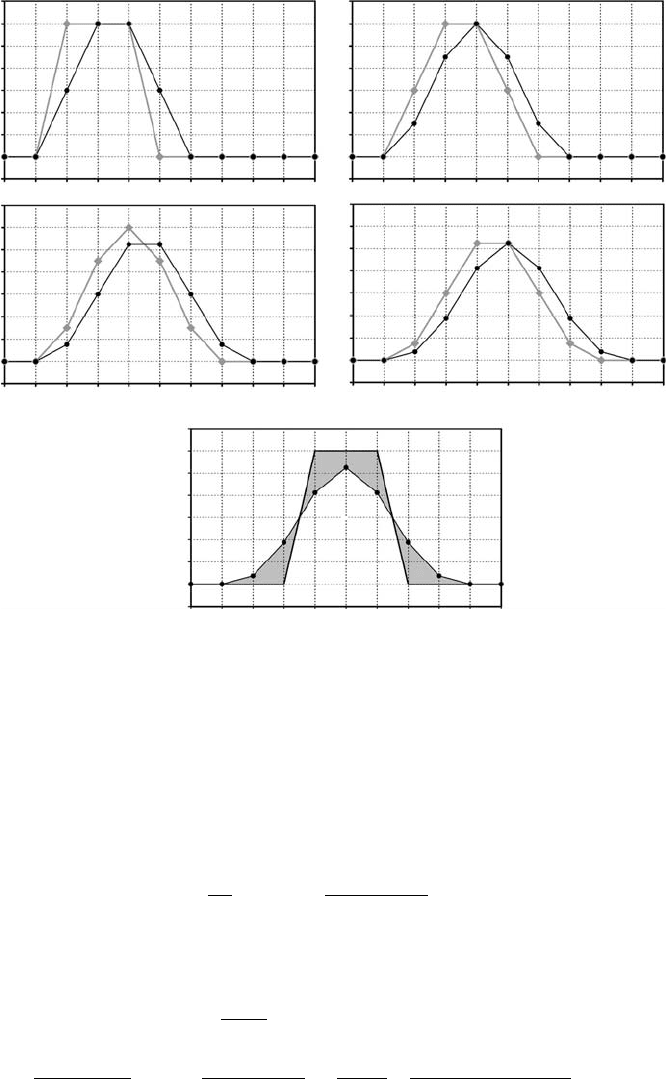
Fig. 8.2 Stencil of a 1D grid used for the discretisation of the Eulerian advection

equation with upwind (a), central (b) and downwind (c) differences.

Therefore, smaller time steps give more numerical diffusion for the same total

duration of advection (compare Fig. 8.1(b) and (c)). On the other hand, to ensure

stability of the numerical solution, the time step should be sufﬁciently small to

satisfy the time limitation condition

t ≤

x

, (8.5a)

which states that the material should not move for more than one grid step per

one time step (this is also called the Courant criteria). Condition (8.5a) should be

satisﬁed in every Eulerian point to prevent oscillations (Fig. 8.1(d)). Therefore,

one should use the minimal ratio between local grid step (which can be variable)

and local ﬂow velocity (which can be variable as well) found in a model. In 2D

and 3D, this limitation may be even stricter

t ≤

x

(8.5b)

to prevent artiﬁcial oscillations from appearing in the numerical solutions.

Figure 8.3 shows the progress of numerical diffusion during only four time steps.

Upwind differences (Eq. 8.4, Fig. 8.2(a)) are applied along with a constant time

step (t = 1/2x/v

), which results in the FD formulation:

t+t

= ρ

−

− ρ

i−1

, (8.6)

108 The advection equation and marker-in-cell method

t = 0

t = 0.5

t = 1

t = 1.5

t = 0.5

t = 1

t = 1.5

t = 2

3300

3350

3250

3200

3150

3100

3050

3000

2950

3300

3350

3250

3200

3150

3100

3050

3000

2950

3300

3350

3250

3200

3150

3100

3050

3000

2950

3300

3350

3250

3200

3150

3100

3050

3000

2950

012345678910

exact

diffusion

t = 2

x, m x, m

x, m

numerical

12345678910

3300

3350

3250

3200

3150

3100

3050

3000

2950

012345678910

ρ, kg/m

(a)

(c)

(b)

(d)

(e)

Fig. 8.3 Progress (a)–(d) in the development of the numerical diffusion during four

time steps (t = 1/2x/v

= 0.5 s) in the case of a 1D advection of a square

density wave, with constant velocity (v

= 1 m/s) on a regular Eulerian grid

(x = 1m).

which results in strong numerical diffusion (Fig. 8.3(e)). The diffusion term, hidden

in Eq. 8.4, can be ‘exposed’ by analysing this equation on the basis of symmetrical

central differences



∂ρ

∂x



central

i+1

− ρ

i−1

2x

Eq. 8.4 can be reformulated as follows

t+t

= ρ

−

t

2x



2ρ

− 2ρ

i−1

+ ρ

i+1

− ρ

i+1



, (8.7a)

t+t

− ρ

t

=−v

i+1

− ρ

i−1

2x

x



i−1

− 2ρ

+ ρ

i+1

x



, (8.7b)

8.2 Eulerian advection methods 109

taking that



∂

∂x



i−1

− 2ρ

+ ρ

i+1

x

we obtain



∂ρ

∂t



=−v



∂ρ

∂x



central

+ D



∂

∂x



, (8.7c)

where D = v

x/2 is the numerical diffusion coefﬁcient. This means that upwind

differences inherently contain numerical diffusion compared to central differences.

On the other hand, applying central and downwind differences for solving the

Eulerian advection equation:

central FD (Fig. 8.2(b)): ρ

t+t

= ρ

− v

t

i+1

− ρ

i−1

2x

, (8.8)

downwind FD (Fig. 8.2(c)): ρ

t+t

= ρ

− v

t

i+1

− ρ

x

, (8.9)

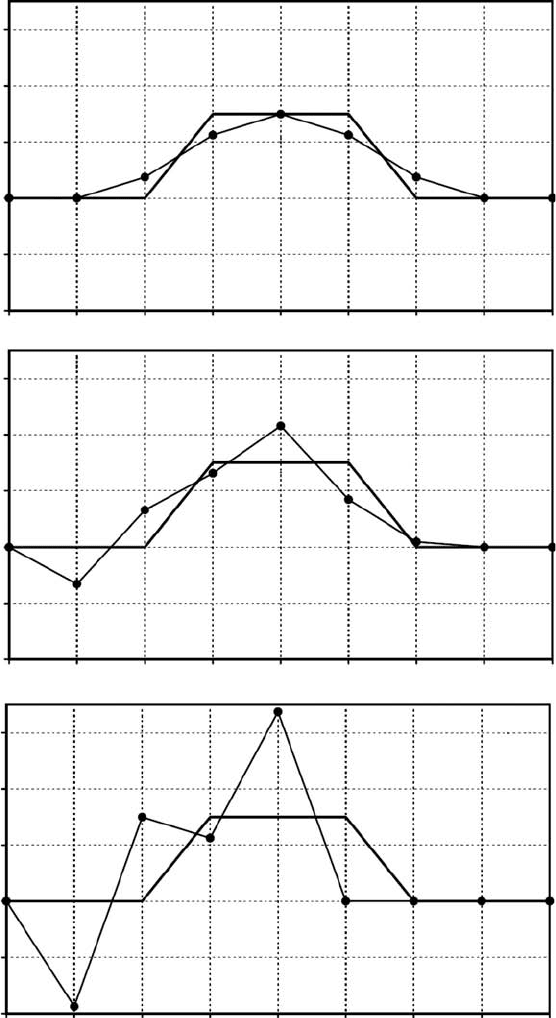
results in a strong oscillation of the numerical solution compared to the exact one

(Fig. 8.4(b),(c)), which is even more dramatic than the numerical diffusion prob-

lem which is characteristic for upwind differences (compare Fig. 8.4(a),(b),(c)).

The oscillations are caused by the erroneous evaluation of the spatial derivative

of density. With both central and downwind differences (in contrast to upwind

differences), we take into account the density distribution in the outgoing material

ﬂow which is useless for predicting density distribution in the incoming material

ﬂow.

One way to minimise numerical diffusion for the Eulerian advection equation is

to use higher-order numerical schemes such as the Flux-Corrected Transport (FCT)

algorithm (Boris and Book, 1973). The FCT is a conservative shock-capturing

scheme that can, in particular, be used for solving the advection equation. An FCT

algorithm consists of two stages, (I) a transport stage and (II) a ﬂux-corrected

anti-diffusion stage. The numerical diffusion errors introduced in the ﬁrst stage

are corrected by the anti-diffusion stage. The implementation of the FCT is more

complex than for upwind FD and is based on more nodal points (Fig. 8.5). For

the case of constant velocity and constant grid spacing, the algorithm of updating

advected parameters (e.g. density) on an Eulerian grid is as follows;

(I) Transport stage – using highly diffusive mass-conservative advection scheme (such as

upwind differences, Eqs. (8.4), (8.7)) to obtain preliminary values of density ( ˜ρ

t+t

)

at the next time instant t +t

˜ρ

t+t

= ρ

− v

t

i+1

− ρ

i−1

2x

+ Dt



i−1

− 2ρ

+ ρ

i+1

x



, (8.10)

where D =

x

t





t

x





is a numerical diffusion coefﬁcient.

exact

upwind differences

downwind differences

central differences

t = 1

x, m

numerical

3600

3400

3200

3000

2800

2600

012345678

ρ, kg/m

3600

3400

3200

3000

2800

2600

ρ, kg/m

3600

3400

3200

3000

2800

2600

ρ, kg/m

(a)

(b)

(c)

Fig. 8.4 Deviation of the numerical solution from the exact one after only two

time steps in the case of upwind (a) central (b) and downwind (c) ﬁnite differences

for advection of a square wave. The best results are, indeed, obtained by upwind

differences, while downwind FD yield strong numerical oscillations. Parameters

are as in Fig. 8.3.

8.2 Eulerian advection methods 111

i–1 ii–2 i+1 i+2

∆x ∆x ∆x ∆x

−2

∼

−1

∼

i +1

∼

i +2

i +1

i +2

−2

−1

−1/2

+1/2

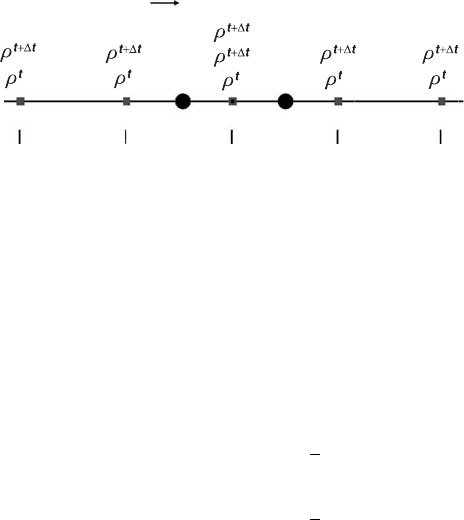
Fig. 8.5 Stencil of a 1D grid used for discretisation of the Eulerian advection

equation with FCT algorithm.

(II) Anti-diffusion stage – correcting the numerical diffusion introduced during the trans-

port stage by deﬁning anti-diffusive ﬂuxes to the left (f

i−1/2

), and to the right (f

i+1/2

)

of the nodal point i,

t+t

= ˜ρ

t+t

− f

i+1/2

+ f

i−1/2

, (8.11)

where

i−1/2

= S

i−1/2

max



0, min



i−1/2

 ˜ρ

t+t

i−3/2



 ˜ρ

t+t

i−1/2



i−1/2

 ˜ρ

t+t

i+1/2



i+1/2

= S

i+1/2

max



0, min



i+1/2

 ˜ρ

t+t

i−1/2



 ˜ρ

t+t

i+1/2



i+1/2

 ˜ρ

t+t

i+3/2



 ˜ρ

t+t

i−3/2

= ˜ρ

t+t

i−1

− ˜ρ

t+t

i−2

 ˜ρ

t+t

i−1/2

= ˜ρ

t+t

− ˜ρ

t+t

i−1

 ˜ρ

t+t

i+1/2

= ˜ρ

t+t

i+1

− ˜ρ

t+t

 ˜ρ

t+t

i+3/2

= ˜ρ

t+t

i+2

− ˜ρ

t+t

i+1

i−1/2

= sign



 ˜ρ

t+t

i−1/2



i+1/2

= sign



 ˜ρ

t+t

i+1/2



Here, sign(A) is a function that gives −1, 0 and 1 if A < 0, A = 0andA > 0,

respectively.

The FCT algorithm stencil (Fig. 8.5) involves ﬁve nodal points in a 1D grid,

compared to two nodal points in the case of upwind differences (Fig. 8.2(a)).

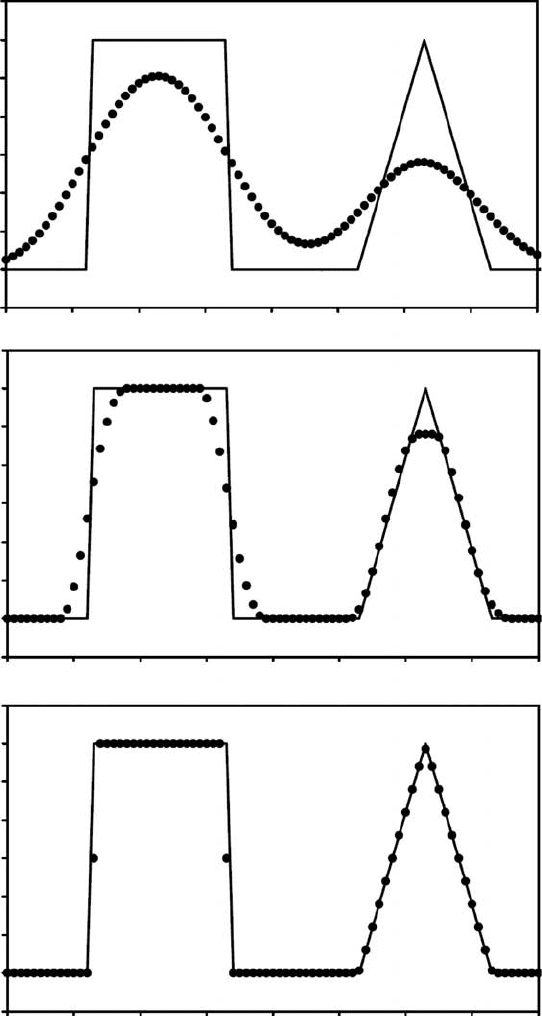
FCT stabilises the numerical diffusion (i.e. advected wave shape stops changing

after some amount of time steps) and gives noticeably better results compared to

upwind differences (compare Fig. 8.6(a) and (b)). These results, however, are still

not perfect and depend on the exact shape of the advected structures (e.g. triangular

waves are subjected to a noticeable decrease in amplitude compared to square

exact

upwind differences (800 time steps)

marker-in-cell method (800 time steps)

FCT (800 time steps)

x, m

numerical

3250

3300

3350

3200

3150

3100

3050

3000

2950

50 60 70 80 90 100 110 120 130

3250

3300

3350

3200

3150

3100

3050

3000

2950

50 60 70 80 90 100 110 120 130

3250

3300

3350

3200

3150

3100

3050

3000

2950

50 60 70 80 90 100 110 120 130

ρ, kg/m

(a)

(b)

(c)

Fig. 8.6 1D advection of a square and triangular density waves with upwind

differences (a), FCT (b) and marker-in-cell method (c). The results have been

obtained with the programs Upwind_1D.m, FCT_1D.m and Markers_1D.m.

8.3 Marker-in-cell techniques 113

i−1 i+1

x x

+ t

Fig. 8.7 Stencil of 1D Eulerian–Lagrangian grid used for advection with the

marker-in-cell technique. Mobile Lagrangian markers (open squares) move with

a prescribed velocity v

and carry information on material density. At every time

step, the density at the Eulerian nodes is interpolated from markers found within

two grid cells around the nodes.

waves, Fig. 8.6(b)). It should also be mentioned that various existing higher-order

Eulerian schemes such as FCT do not eliminate numerical diffusion completely,

but rather stabilise it to a certain acceptable level (Fig. 8.6(b)).

8.3 Marker-in-cell techniques

If numerical diffusion needs to be strongly minimised, Lagrangian and Eulerian–

Lagrangian advection algorithms can be used. In geomodelling, for example, very

accurate advection of non-diffusive properties such as rock type (composition)

with strongly discontinuous (e.g., layering) distribution in space is often required.

One of the most popular methods in this case is to combine the use of Lagrangian

advecting points (markers, tracers or particles) with an immobile, Eulerian grid

(e.g., Woidt, 1978; Christensen, 1982; Schmeling, 1987; Weinberg and Shmelling,

1992). In this approach, properties are initially distributed on a large amount of

Lagrangian points that are advected according to a given/computed velocity ﬁeld.

The advected material properties (e.g. density) are then interpolated from the

displaced Lagrangian points to the Eulerian grid (Fig. 8.7) by using a weighted-

distance averaging such as the following linear interpolation formula

t+t



m(i)



m(i)

= 1 −

x

m(i)

x

(8.12)

where w

m(i)

is the weight of the m-th marker for the i-th node, x

m(i)

denotes the

distance from the m-th marker, to the i-th node. In 1D, the density at an Eulerian

node is interpolated only with the markers found in the two surrounding cells (i.e.

114 The advection equation and marker-in-cell method

within one grid space from the node). For a more local interpolation, fewer markers

found within the surrounding cell (e.g. half grid space from the node) can be used.

This method is called the marker-in-cell (MIC) technique. Obviously, the results

of pure advection (e.g. of density, Fig. 8.6(c)) with MIC are not subjected to

numerical diffusion (with the exception of non-accumulating interpolation errors

between Lagrangian markers and Eulerian nodes) since markers always retain their

original density values and only change positions with time.

In order to move a Lagrangian marker A, different advection schemes can be

used. The most simple is the ﬁrst-order accurate advection scheme

t+t

= x

+ v

t, (8.13a)

t+t

= y

+ v

t, (8.13b)

t+t

= z

+ v

t, (8.13c)

where x

, y

and z

are the coordinates of marker A at the current time (t); x

t+t

and z

t+t

are the coordinates of the same marker at the next moment in time

(t + t); v

and v

are components of the material velocity vector at the

point A, at time t. The velocity of the Lagrangian point A can signiﬁcantly change

during the displacement if there is a strong spatial variation of the velocity ﬁeld.

In this case, a ﬁrst-order advection scheme will not be very accurate. This problem

can be rectiﬁed, by either using smaller time steps (t), or by using higher-order

advection schemes.

One of the most popular in geomodelling is the Runge–Kutta advection scheme,

given as

t+t

= x

+ v

eff

t, (8.14a)

t+t

= y

+ v

eff

t, (8.14b)

t+t

= z

+ v

eff

t, (8.14c)

where v

eff

, v

eff

and v

eff

are components of the effective material velocity vector for

the point A over the period between current (t) and next (t +t) moments of time.

Components of the effective material velocity are computed by using the material

velocity at several different points in space (varying from 2 to 4, depending on the

order of the scheme).

The second-order Runge–Kutta scheme uses two points (A and B)

eff

= v

, (8.15a)

eff

= v

, (8.15b)

eff

= v

, (8.15c)

8.3 Marker-in-cell techniques 115

where the coordinates of point B are computed as

= x

+ v

t

= y

+ v

t

= z

+ v

t

. (8.15d)

The third-order Runge–Kutta scheme uses three points (A, B and C)

eff

(

+ 4v

+ v

)

, (8.16a)

eff

+ 4v

+ v

), (8.16b)

eff

+ 4v

+ v

), (8.16c)

where the coordinates of points B and C are computed as

= x

+ v

t

= y

+ v

t

= z

+ v

t

, (8.16d)

= x

+ (2v

− v

)t, y

= y

+ (2v

− v

)t,

= z

+ (2v

− v

)t. (8.16e)

And ﬁnally, the classical fourth-order Runge–Kutta scheme uses four points (A, B,

C and D)

eff

+ 2v

+ v

), (8.17a)

eff

+ 2v

+ v

), (8.17b)

eff

+ 2v

+ v

), (8.17c)

where the coordinates of points B, C and D are computed as

= x

+ v

t

= y

+ v

t

= z

+ v

t

, (8.17d)

= x

+ v

t

= y

+ v

t

= z

+ v

t

, (8.17e)

= x

+ v

t, y

= y

+ v

t, z

= z

+ v

t. (8.17f)

The last advection scheme is very accurate in space (fourth-order accuracy) but less

accurate in time (ﬁrst-order accuracy) if the velocity ﬁeld for the current moment

of time (i.e. A-conﬁguration velocity ﬁeld) is used for B, C and D points. An

alternative algorithm is to use the Runge–Kutta scheme in both space and time:

all markers are ﬁrst displaced to their B points and then material properties are re-

interpolated to Eulerian nodes and a new B-conﬁguration velocity ﬁeld is computed

by solving the momentum and continuity equations, this B-velocity ﬁeld is then

used for moving markers to their C points for computing a C-conﬁguration velocity

116 The advection equation and marker-in-cell method

m-th-marker

ij-th-node

j+1

i+1

Fig. 8.8 Stencil of 2D grid used for the interpolation of physical properties from

the markers to the nodes. The dashed boundary indicates the area from which

markers are used for interpolating properties to node (i, j ) in the case of a local

interpolation scheme.

ﬁeld etc. Obviously this approach is computationally more expensive. Therefore, in

the case of non-steady ﬂows (i.e. with strong variations in velocity ﬁeld with time),

ﬁrst-order advection schemes with smaller time step are indeed more efﬁcient.

Various interpolation schemes can be used to interpolate physical properties

(e.g., density, viscosity, heat capacity) from the Lagrangian markers to the Eulerian

nodes. The following standard ﬁrst-order accurate bilinear scheme is often used to

calculate an interpolated value of a parameter B

(i, j )

for the ij-th-node using values

) assigned to all markers found in the four surrounding cells (Fig. 8.8)

i,j



m(i,j)



m(i,j)

(8.18)

m(i,j)



1 −

x





1 −

y



where w

m(i, j )

represents a statistical weight of the m-th-marker at the ij-th-node;

x

and y

are the distances from the m-th-marker to the ij-th-node. It is worth

mentioning that the use of a higher-order interpolation scheme (e.g. Fornberg, 1995)

produces undesirable numerical ﬂuctuations in scalar, vector and tensor properties

interpolated at the proximity of sharp transitions. This scenario frequently occurs

in geodynamic models, hence the ﬁrst-order interpolation is preferred. A more

local interpolation from markers to nodes can again be obtained by using fewer

markers located within a limited (e.g. half grid space, see dashed boundary in

Fig. 8.8) range of the vertical and horizontal distances around an Eulerian node.