Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

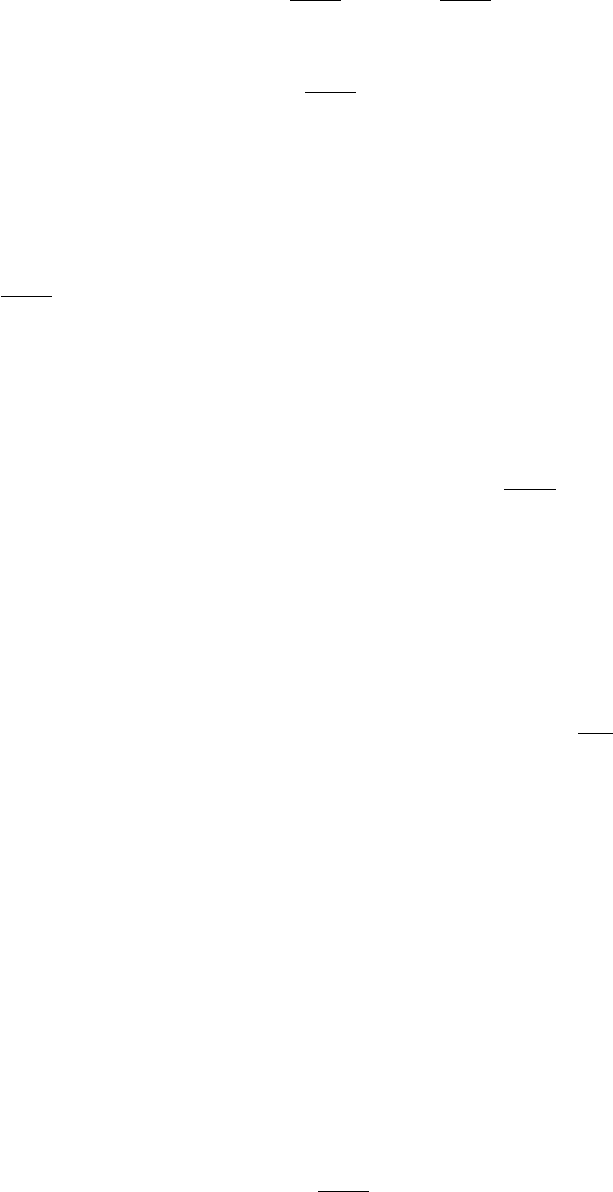
derivative, and denote it by

δW

δx(t)

[x] or

δ

δx(t)

W [x] (15)

so in this case, we can write

δW

δx(t)

[x] = 2

³

x(t) − t

´

(16)

Notice that the t dependence of the RHS of (16) comes from the t dependence of the differential

in the denominator of the LHS — again W [x] for some particular x is just a number with no t

dependence.

This deﬁnition of functional derivative is generally useful, so let’s discuss it in general:

δ

δx(t)

W [x] is the coefﬁcient of the linear term in δx(t) in W [x + δx]. (17)

This is a reasonable deﬁnition because it makes the functional Taylor series work in the same way

that the ordinary Taylor series does. In terms of the functional derivative, the functional Taylor

series starts like this:

W [x + δx] = W [x] +

Z

t

2

t

1

dt δx(t)

δ

δx(t)

W [x] + ··· (18)

In words, this says that the total change in the functional is obtained by adding up (actually in-

tegrating because the variable is continuous) the small changes δx(t ) in x(t) at each point times

the rate of change of the functional at that point. This is just what we always say, except that the

number of variables has become continuously inﬁnite. (18) is precisely analogous to the Taylor

series for functions of several variables that we will discuss in the appendix and in future lectures:

F (x

1

+ ∆x

1

, x

2

+ ∆x

2

, ···) = F (x

1

, x

2

, ···) +

X

j

∆x

j

∂

∂x

j

F (x

1

, x

2

, ···) + ··· (19)

The only difference is that instead of the sum over all the different variables that we have in (19),

in (18) we need an integral over t because in effect, the value of x(t) at each value of t is a separate

variable.

Finding functional derivatives

In general, functional derivatives can be difﬁcult to ﬁnd, but it is easy to ﬁnd them for functionals

like W [x] that have the form of an integral of an ordinary function —

W [x] =

Z

t

2

t

1

dt F

³

x(t)

´

(20)

In this case, the functional derivative of W [x] is related to the ordinary derivative of F —

δW

δx(t)

[x] = F

0

³

x(t)

´

(21)

6

The reason this is so simple is that we can calculate the functional Taylor expansion of W using

the ordinary Taylor expansion of F , and looking for the coefﬁcient of δx(t). Let’s show how this

works.

W [x + δx] =

Z

t

2

t

1

dt F

³

x(t) + δx(t)

´

(22)

But using the ordinary Taylor expansion for the ordinary function F (x), the right hand side be-

comes

=

Z

t

2

t

1

dt

h

F

³

x(t)

´

+ δx(t) F

0

³

x(t)

´

+ ···

i

(23)

Picking out the coefﬁcient of δx(t) on the right hand side gives (21). Notice the way that the

variable t gets promoted from being a dummy variable in (20) and (22) to being a real variable in

(23). We single out a particular value of t when we ﬁnd the coefﬁcient of δx(t) for that t.

The function F in (20) may depend on other functions of t, in which case we can generalize

(20) as follows:

δ

δx(t)

Z

t

2

t

1

dt

0

F

³

x(t

0

), y(t

0

), ···

´

=

∂

∂x

F (x, y(t), ···)|

x=x(t)

(24)

where . . . denotes and other functions that F depends on. Note that in (24), t

0

is a dummy index,

integrated over so that it could be called anything except t. The dependence on t is real (not

dummy) because the process of functional differentiation picks out a value of t. Here are some

examples:

F [x] =

Z

t

2

t

1

dt

0

x(t

0

)

3

⇒

δ

δx(t)

F [x] = 3 x(t)

2

F [x] =

Z

t

2

t

1

dt

0

sin

³

x(t

0

)

´

⇒

δ

δx(t)

F [x] = cos

³

x(t)

´

F [x, y] =

Z

t

2

t

1

dt

0

³

x(t

0

) y(t

0

)

´

3

⇒

δ

δx(t)

F [x, y] = 3 x(t)

2

y(t)

3

F [x, y] =

Z

t

2

t

1

dt

0

sin

³

x(t

0

) y(t

0

)

´

⇒

δ

δx(t)

F [x, y] = y(t) cos

³

x(t) y(t)

´

(25)

We can summarize these ideas by saying that when the functional is the integral of an ordi-

nary function, what the functional derivative does is to eliminate the integral and differentiate the

function. Think about it in the context of the examples in (25).

Back to Hamilton’s principle

With this new tool of the calculus of variations, we can go back and consider Hamilton’s principle.

Remember that what we want to do is to show that the functional S[x] has zero variation around

the same trajectory that we get by using F = ma.

According to our discussion, what we want to do to impose vanishing variation on S[x] is to

set the functional derivative of S[x],

δS

δx(t)

(26)

7

to zero. As in the simpler example, we calculate the functional derivative by performing a func-

tional Taylor series and picking out the coefﬁcient of δx(t). For pedagogical purposes, we will

break this up into two pieces:

S = S

T

− S

V

(27)

where

S

T

[x] ≡

Z

t

2

t

1

dt

·

T

³

˙x(t)

´

¸

=

Z

t

2

t

1

dt

m

2

³

˙x(t)

´

2

(28)

and

S

V

[x] ≡

Z

t

2

t

1

dt

·

V

³

x(t)

´

¸

=

Z

t

2

t

1

dt V

³

x(t)

´

(29)

For the S

V

term, because V does not depend on ˙x, this is just like the W [x] example,

δS

V

δx(t)

= V

0

³

x(t)

´

(30)

This is a good sign because the derivative of the potential is related to the force.

For the S

V

, term, we will need an extra step, so let’s write out the functional Taylor series in

detail.

S

T

[x + δx] =

Z

t

2

t

1

dt

m

2

³

˙x(t) + δ ˙x(t)

´

2

(31)

=

Z

t

2

t

1

dt

m

2

³

˙x(t)

´

2

+

Z

t

2

t

1

dt δ ˙x(t) m ˙x(t) + O(δx

2

) (32)

= S

T

[x] +

Z

t

2

t

1

dt δ ˙x(t) m ˙x(t) + O(δx

2

) (33)

But the δ ˙x(t) in (33) is the change in ˙x(t) when we make a change δx(t) in x(t). Thus since

d

dt

³

x(t) + δx(t)

´

= ˙x(t) +

d

dt

δx(t) (34)

δ ˙x(t) is given by

δ ˙x(t) =

d

dt

δx(t) . (35)

The trouble with (33) is that it depends on δ ˙x(t), while we have deﬁned the functional derivative

to be the coefﬁcient of δx(t). To take care of that, we can integrate by parts:

Z

t

2

t

1

dt δ ˙x(t) m ˙x(t) =

Z

t

2

t

1

dt

Ã

d

dt

δx(t)

!

m ˙x (t)

=

Z

t

2

t

1

dt

d

dt

³

δx(t) m ˙x(t)

´

−

Z

t

2

t

1

dt δx(t) m ¨x(t)

= −

Z

t

2

t

1

dt δx(t) m ¨x(t) + δx(t

2

) m ˙x(t

2

) − δx(t

1

) m ˙x(t

1

)

(36)

The last line in (36) has two terms from the endpoints of the integration. These don’t look like

everything else, and we want to get rid of them. This is where (4) comes in. We are supposed to

8

be restricting our attention to functions satisfying (4). But if x(t) and x(t) + δx(t) both satisfy (4),

then

δx(t

1

) = δx(t

2

) = 0 . (37)

In words, we are only interested in variations that vanish at the endpoints. These functions might

look something like this

x

1

x

2

t

1

t

2

.

..

....

.

..

......

.

..

....

.

.....

.

..

...

......

..

.

x(t)

x(t) + δx(t)

δx(t)

So in fact, the funny looking terms vanish because of (4). Then (36) becomes

Z

t

2

t

1

dt δ ˙x(t) m ˙x(t) = −

Z

t

2

t

1

dt δx(t) m ¨x(t) (38)

Now we can pick out the coefﬁcient of δx(t) and see that

δS

T

δx(t)

= −m ¨x(t) (39)

Now, ﬁnally, we can verify that Hamilton’s principle is correct. Putting (30) and (39) together,

we have that the condition for vanishing variation of S[x] is

δS

δx(t)

= −m ¨x(t) −V

0

³

x(t)

´

= 0 (40)

or

m ¨x(t) = −V

0

³

x(t)

´

(41)

which, since F = −V

0

, is just Newton’s second law!!!

More degrees of freedom

It is easy to see that Hamilton’s principle works just as well for more particles, or in more dimen-

sions. Suppose, for example, that there are n particles, so that

T =

n

X

j=1

m

j

2

˙x

2

j

and V = V (x

1

, ···, x

n

) (42)

9

Then it is easy to see by the same sort of arguments that

δS

δx

j

(t)

= −m

j

¨x

j

(t) − V

j

³

x

1

(t), ···, x

n

(t)

´

(43)

where

−V

j

(x

1

, ···, x

n

) = −

∂

∂x

j

V

j

(x

1

, ···, x

n

) (44)

is the force on particle j. For S[x] to have vanishing variation, we must have (43) vanish for each

j, which just gives F = ma for each particle.

The Lagrangian and the action

As we will see, Hamilton’s principle really captures more of what is going on in the world than

F = ma. It is worth going over the consequences of Hamilton’s principle again in a more general

language. In general, the combination T − V is called the Lagrangian, L. S[x], as I said above,

is called the action,

S[x] =

Z

t

2

t

1

dt L

³

x(t), ˙x(t )

´

(45)

Here, x might actually have indices that allows it to represent more than one particle or dimension

or both. We won’t write them explicitly in this formal derivation. Now we want the functional

derivative of S[x] with respect to x(t) to vanish. In general, the functional derivative is

δS

δx(t)

[x] =

∂

∂x(t)

L

³

x(t), ˙x(t )

´

−

d

dt

∂

∂ ˙x(t)

L

³

x(t), ˙x( t)

´

(46)

The ﬁrst term arises from the Taylor expansion of the x(t) dependence. The second term arises in

the same way as (39), from the Taylor expansion of the ˙x(t) dependence, followed by an integration

by parts, which gives the minus sign. Thus Hamilton’s principle implies that the solution for the

motion satisﬁes

∂

∂x(t)

L

³

x(t), ˙x(t )

´

−

d

dt

∂

∂ ˙x(t)

L

³

x(t), ˙x(t )

´

= 0 (47)

If x has several components, (47) must be true for each component separately.

The equation (or set of equations) (47) is called the Euler-Lagrange equation. We have seen

that in simple situations this equation is just a trivial rewriting of F = ma. However, there are

several important advantages to thinking about mechanics in terms of Hamilton’s principle, and

deriving the Euler-Lagrange equation, rather than using Newton’s second law directly.

1. The mathematics is kind of cool! In this course, we will just give you a small taste of

the beautiful mathematical structure of mechanics that was worked out in the 19th century.

If you like this sort of thing, you can look forward to a feast in Physics 151, where it is

described in more depth.

2. It is often easier to write down the kinetic and potential energies than to understand all of the

forces. Thus Hamilton’s principle can be a labor saving device.

10

3. In general, there may be many different ways of representing the conﬁguration of a physical

system, and thus many ways of choosing the variables that describe the system. Hamilton’s

principle makes it obvious that the particular choice of variables doesn’t matter, because

S[x], whose vanishing variation determines the trajectories, is just a single number that

doesn’t depend on how we choose to describe the system. This will be especially useful

when we work in spherical or cylindrical coordinate, which are more appropriate to some

problems.

4. More generally, Hamilton’s principle makes it very easy to understand the consequences of

symmetry. We will use it to see that there is a deep connection between symmetries and

conservation laws like conservation of momentum or angular momentum. I happen to love

symmetry (as will become apparent as the course goes on if it is not already obvious), so this

is one of my favorites.

5. Sometimes, we don’t know or care about all the forces in a mechanical system. This of-

ten happens when there is a constraint. There are many examples, like a bead sliding on a

frictionless wire, or a particle moving on the surface of the earth, where the system is con-

strained by some forces that we don’t understand in detail. We can use Hamilton’s principle

to solve such problems without even computing the constraining forces by simply choosing

coordinates that automatically incorporate the constraints — we’ll do some examples, and

there are more in David Morin’s notes.

The most compelling argument for Hamilton’s principle is none of the above, but a deeper, philo-

sophical one.

Quantum mechanics and the classical trajectory

In my view, the most important reason that Hamilton’s principle and the Lagrangian are so im-

portant has to do not with classical mechanics alone, but with quantum mechanics and the way in

which classical physics emerges as an approximation to the quantum world.

From the classical point of view, Hamilton’s principle is actually a little peculiar. Why should

it matter to a classical particle what the value of the action is for paths that the particle does not

actually take? OK – - so Hamilton’s principle works to give the classical equation of motion, but

it is hard to ﬁgure out what it means physically. But in quantum mechanics, it has a very deﬁnite

meaning, because in quantum mechanics, the particle really takes all paths! This is absolutely

nutty, but this is really the way the world works. Roughly, the way it works is this. When a

quantum mechanical particle moves from point x

1

at time t

1

to point x

2

at time t

2

, it takes all

trajectories from the starting point to the end simultaneously. But the different trajectories can add

together like the different ripples in a wave on a pond. Associated with each trajectory there is a

complex number A whose phase is the action divided by ¯h, Planck’s constant over 2π.

e

iS[x]/¯h

(48)

The most likely trajectories are those that are near the classical trajectory, because the action is

changing very slowly for these trajectories, they have approximately the action of the classical

trajectory, and therefore all the As have the same phase and all the nearby trajectories add up

11

coherently. Trajectories very far from the classical trajectory are unlikely because the phase is

changing rapidly and nearby trajectories have different phases and add nearly to zero.

There is another way of putting this that is perhaps more interesting. Euler-Lagrange equations

are differential equation, but not every differential equation is an Euler-Lagrange equation. The

fact that the world is quantum mechanical explains why the classical physics that we see can

be described by the solutions not just to any old differential equation, but speciﬁcally to Euler-

Lagrange equations. We will see why this distinction is important as we go along.

Appendix: On the functional Taylor series

It might be useful for some of you if I expand on the statement of the functional Taylor series

because it a pretty piece of math. Some of you, on the other hand, may ﬁnd this rather terrifying.

Please DON’T PANIC. This section is called an appendix because it is completely optional. I

probably won’t get to it at all in lecture. But for some of you it may be fun.

The picture of the functional Taylor series that I will give you is related to the following state-

ment that you may ﬁnd useful. The t in a function x(t) can be thought of as a kind of index,

labeling components of an inﬁnite dimensional vector. Or to put this the other way around, a vec-

tor ~r can be thought of as a function of the index that labels the component — r

j

is a number for

each j just like x(t) is a number for each t. In this way of thinking, a functional, W [x] is like a

function of several variables, f(r

1

, ···, r

n

) (depending on an n-dimensional “vector”), except that

W [x] depends on an inﬁnite number of variables, the values of x(t) for some range of t. Now what

does the Taylor expansion look like for a function of several variables, like f(r

1

, ···, r

n

)? We can

build up the Taylor series by looking at one variable at a time:

f(r

1

+ a

1

, ···, r

n

) =

Ã

1 + a

1

∂

∂r

1

+

1

2

a

2

1

∂

2

∂r

2

1

+ ···

!

f(r

1

, ···, r

n

)

f(r

1

+ a

1

, r

2

+ a

2

, ···, r

n

) =

Ã

1 + a

2

∂

∂r

2

+

1

2

a

2

∂

2

∂r

2

+ ···

!

f(r

1

+ a

1

, r

2

, ···, r

n

)

and so on for all n variables

(49)

This looks complicated, but it can be simpliﬁed easily using a very beautiful form for the Taylor

expansion of one variable:

g(x + a) = exp

Ã

a

∂

∂x

!

g(x) =

∞

X

k=0

a

k

k!

d

k

dx

k

g(x) (50)

The expansion of the exponential precisely reproduces the terms in the Taylor expansion. Using

(50), equation (49) becomes

f(r

1

+ a

1

, ···, r

n

+ a

n

) =





n

Y

j=1

exp

Ã

a

j

∂

∂x

j

!





f(r

1

, ···, r

n

) (51)

But because the product of exponentials is the exponential of the sum of the exponents, this can be

written as

f(r

1

+ a

1

, ···, r

n

+ a

n

) = exp





n

X

j=1

a

j

∂

∂x

j





f(r

1

, ···, r

n

) (52)

12

This is the Taylor series for more than one variable. It is rather neat that it looks just like the Taylor

series for a single variable, (50), except that we have to include derivatives with respect to all the

variables in the exponent. Now for an inﬁnite number of variables labeled by a continuous variable

t, in some range t

1

≤ t ≤ t

2

, the argument goes the same way, but instead of summing over the

indices, as we do in (52), we must integrate over the continuous variable t, so that the functional

Taylor series looks like

W [x + δx] = exp

Ã

Z

t

2

t

1

dt δx(t)

δ

δx(t)

!

W [x] (53)

Note that if we expand the exponential, we get a ﬁrst term which is just (18), as expected from

our earlier discussion.

13

lecture 7

Topics:

Where are we now?

The Lagrangian and Euler-Lagrange equations

Example - bead on a expanding ring

Example - bead on a rotating rod

More degrees of freedom

Example - frictionless table

Generalized Force and Momentum

Example - Reduced mass and center of mass

Energy again

Example - Atwood’s machine

Where are we now?

In the last lecture, I tried to convince you that Hamilton’s principle and the Euler-Lagrange equa-

tion captures what is really going on in classical mechanics, because it arises as the classical limit

of quantum mechanics. In this lecture, we will ﬁrst describe how energy conservation arises from

Lagrangians that do not depend explicitly on time. We will then go on to discuss the conservation

laws that arise when the Lagrangian does not depend on some coordinate. In particular, we will

discuss momentum conservation

I have included a lot in the notes for this lecture that we will probably not get to discuss in

any detail, just to give you more resources to use for the upcoming exam (both the take-home and

in-class parts). I have also included a number of appendices, which I will not discuss in lecture at

all, but which may be useful to read.

The Lagrangian and Euler-Lagrange equations

Let’s begin by going over Hamilton’s principle and the Euler-Lagrange equation again. We begin

by constructing the Lagrangian, L.

L

³

x(t), ˙x( t), t

´

= T

³

x(t), ˙x (t), t

´

− U

³

x(t), ˙x( t), t

´

(1)

Where T and U are the kinetic and potential energies, as functions of the variable x that describes

the conﬁguration of the system, and its time derivative, ˙x. This time I have included the possibility

that these functions also depend explicitly on t. By explicit time dependence, I mean dependence

beyond that coming from the time dependence of x(t). We will come back to this a little later when

we discuss energy.

From the Lagrangian, we construct the action S[x] by integrating in time from an initial time

t

1

to a ﬁnal time t

2

.

S[x] =

Z

t

2

t

1

dt L

³

x(t), ˙x(t), t

´

(2)

1

Then Hamilton’s principle is the statement that the actual trajectory that describes the evolution

of the system from x(t

1

) = x

1

to x(t

2

) = x

2

is the trajectory around which the variation of S[x]

vanishes. What I showed you last time is that we could turn this condition into a differential

equation for the trajectory by setting to zero the functional derivative

δS[x]

δx(t)

=

∂

∂x(t)

L

³

x(t), ˙x(t ), t

´

−

d

dt

∂

∂ ˙x(t)

L

³

x(t), ˙x(t ), t

´

(3)

Thus Hamilton’s principle implies that the solution for the motion satisﬁes

∂

∂x(t)

L

³

x(t), ˙x(t ), t

´

−

d

dt

∂

∂ ˙x(t)

L

³

x(t), ˙x(t ), t

´

= 0 (4)

This is the Euler-Lagrange equation. Hamilton’s principle tell us that the classical trajectory sat-

isﬁes (4). But we are usually interested not in checking that a given solution satisﬁes the Euler-

Lagrange equation, but rather in using the Euler-Lagrange equation to ﬁnd the solution. Then

because (4) is just a differential equation for x(t), it is conventional to drop the explicit time de-

pendence of x and write it as

∂

∂x

L

³

x, ˙x, t

´

−

d

dt

∂

∂ ˙x

L

³

x, ˙x, t

´

= 0 (5)

Solving the differential equation (5) and imposing the initial conditions then gives us x(t).

I hope that you have followed the arguments that lead to the Euler-Lagrange equation, and

are fascinated by the connection to quantum mechanics that I mentioned. But in a way it doesn’t

matter. What is most important for this course is that you understand what the Euler-Lagrange

equation says, and how to get it from the kinetic and potential energies.

Note that once we have used Hamilton’s principle to determine the Euler-Lagrange equation,

we don’t have to impose the initial conditions in the peculiar way we did in Hamilton’s principle by

specifying a beginning and ending position. Any way of specifying the two initial conditions will

do, as long as our solution satisﬁes the differential equation we derived from Hamilton’s principle.

Example - bead on an expanding ring

Let’s warm up by doing a couple of examples of Euler-Lagrange equations for systems with a

single degree of freedom. I’ll begin with a system that is mathematically very simple, but that I

don’t actually know how to build. Suppose we have a small bead with mass m that slides without

a friction on circular ring centered in the x − y plane, but whose radius grows as a function of time

as

r(t) = r

0

+ v t (6)

It will be most useful to analyze this in terms the polar angle θ in terms of which the x and y

coordinates of the bead are

x = r(t) cos θ y = r(t) sin θ (7)

2

Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

Подождите немного. Документ загружается.