Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

We can write the kinetic energy of the bead directly in terms of θ using the fact that the radial

motion of the bead due to the expansion of the ring and tangential motion associated with changing

θ are instantaneously perpendicular, so that ~v

2

can be written as

~v

2

= ˙x

2

+ ˙y

2

= ˙r(t)

2

+ r(t )

2

˙

θ

2

(8)

Remember here that r(t) is not a dynamical variable — the time dependence of r is imposed on

the system from the beginning. There is no potential energy because the system is in a horizontal

plane, so the Lagrangian is

L(θ,

˙

θ, t) =

m

2

³

˙r(t)

2

+ r(t)

2

˙

θ

2

´

(9)

The Euler-Lagrange equation here is particularly simple because the Lagrangian does not depend

at all on θ. Thus

0 =

∂

∂θ

L

³

θ,

˙

θ, t

´

−

d

dt

∂

˙

θ

L

³

θ,

˙

θ, t

´

= −

d

dt

∂

˙

θ

L

³

θ,

˙

θ, t

´

= −

d

dt

³

m r(t)

2

˙

θ

´

(10)

What is nice about (10) is that the solution (or more properly the “ﬁrst integral”) is really simple.

m r(t )

2

˙

θ = a constant (11)

To ﬁnd the constant, we need an initial condition. For example if the angular velocity at t = 0 is

˙

θ(0) = ω

0

, then we can write

m r(t )

2

˙

θ = m r

2

0

ω

0

(12)

thus

˙

θ =

dθ

dt

=

r

2

0

ω

0

(r

0

+ v t)

2

(13)

We can now integrate this to ﬁnd θ(t). Again we need an initial condition. If

θ(0) = θ

0

(14)

then

θ(t) = θ

0

+

Z

t

0

dt

0

r

2

0

ω

0

(r

0

+ v t

0

)

2

= θ

0

+

ω

0

r

0

t

r

0

+ v t

(15)

3

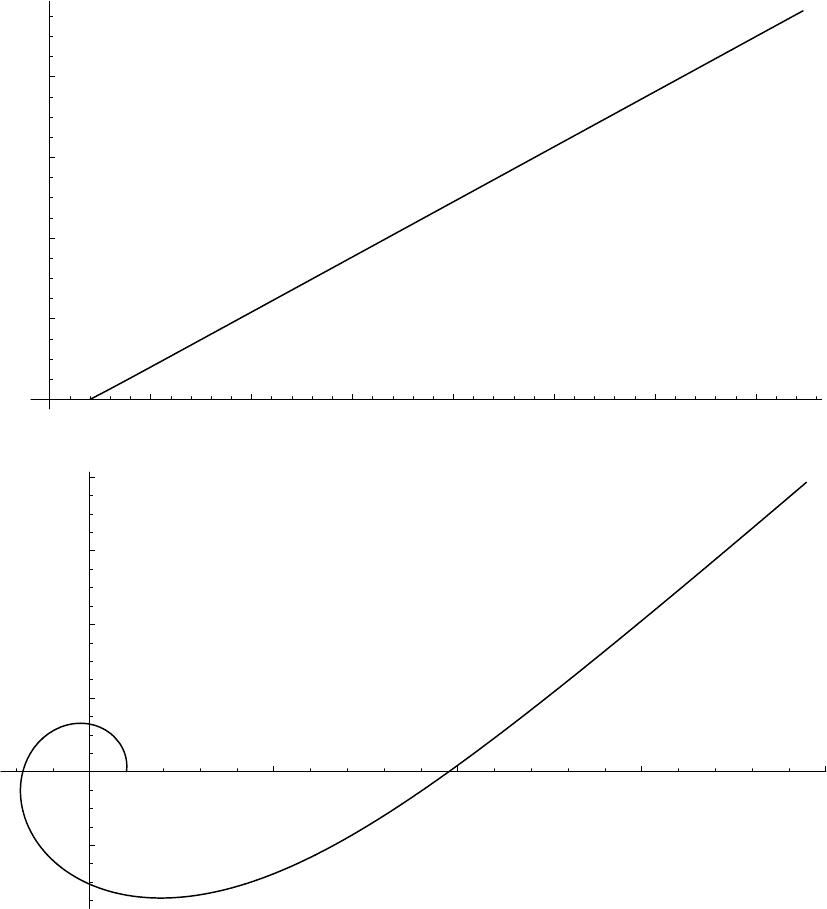
Here are some possible trajectories.

2.5

5 7.5

10 12.5

15 17.5

2

4

6

8

5

10

15

20

-2

2

4

6

8

4

-5 5

10

15

20

-8

-6

-4

-2

2

4

Example - bead on a rotating rod

Next, consider a bead with mass m on a straight frictionless rod that rotates with constant angular

velocity ω. For simplicity, we will let it rotate around the origin in the x-y plane. Then gravity

plays no role. The angle with the x axis at time t is ωt . This would not be a trivial problem if we

were armed only with

~

F = m~a. But with a Lagrangian it is easy. For one thing, the Lagrangian

technique allows us to focus just on where the bead is on the wire. Let ` (which can be negative)

be the distance along the rod where the bead sits at time t. This speciﬁes the conﬁguration of the

system. The position of the bead at time t is then

x = ` cos ωt y = ` sin ωt (16)

The velocity is

˙x =

˙

` cos ωt − `ω sin ω t ˙y =

˙

` sin ωt + `ω cos ω t (17)

Thus the kinetic energy is

1

2

m

³

˙x

2

+ ˙y

2

´

=

1

2

m

³

˙

`

2

+ `

2

ω

2

´

(18)

The explicit time dependence from (17) has gone away when we form the square of velocity. If

you think about the two terms on the right hand side of (18), you will realize that the ﬁrst one is

related to the motion of the bead along the rod, and the second one with the rotation of the rod.

Because these two motions are perpendicular, there is no cross term and the total kinetic energy is

just a sum of the two effects.

In this case, there is no potential, so the Lagrangian is just given by the kinetic energy, (18),

and it doesn’t depend on t explicitly, so we don’t need t in the list of variables,

L(`,

˙

`) =

1

2

m

³

˙

`

2

+ `

2

ω

2

´

(19)

and the Euler-Lagrange equation is

0 = m`ω

2

−

d

dt

(m

˙

`) (20)

5

or

¨

` = ω

2

` (21)

This is a differential equation we can solve easily because it is linear and TTI. The general solution

is

`(t) = C e

ωt

+ D e

−ωt

(22)

You are likely to see this written in term of the so-called hyberbolic functions,

sinh x =

e

x

− e

−x

2

cosh x =

e

x

+ e

−x

2

(23)

These are handy, because they have properties that are reminiscent of the more familiar trigonometic

functions, sin x and cos x. But if you are not used to them, you can always do everything in terms

of exponentials. At any rate, if the bead starts from rest at ` = `

0

at t = 0, the solution looks like

`(t) = `

0

cosh ωt = `

0

e

ωt

+ e

−ωt

2

(24)

Exponentials get big quickly, so this bead gets going pretty fast. For example, in the time π/ω,

while the rod rotates through 180

◦

, the distance from the origin increases by a factor of

cosh π ≈ 11.6 (25)

So this is at good way to launch things.

If instead, the rod rotates with constant angular velocity ω around the origin in the x-z plane in

the earth’s gravitational ﬁeld, then we have to include the effect of gravity - but this is easy. Again,

we take the angle with the x axis at time t is ωt.

The conﬁguration of the system looks the same except that z replaces y. Thus the kinetic

energy looks the same. But now there is a gravitational contribution to the potential energy

U(`, t) = mgz = mg` sin ωt (26)

Thus the Lagrangian in this case depends explicitly on t. It looks like

L(`,

˙

`, t) =

1

2

m

³

˙

`

2

+ `

2

ω

2

´

− mg` sin ωt (27)

and the Euler-Lagrange equation is

0 = m`ω

2

− mg sin ωt −

d

dt

(m

˙

`) (28)

or

¨

` = ω

2

` − g sin ωt (29)

6

More degrees of freedom

We didn’t get to discuss more degrees of freedom in detail last time, and it is sufﬁciently important

that I wanted to go over it slowly and give an example. We will do some more on Tuesday.

Hamilton’s principle works just as well for more particles, or in more dimensions. Suppose that

there are n particles, so that

T =

n

X

j=1

m

j

2

˙x

2

j

and U = V (x

1

, · · · , x

n

) (30)

Then it is easy to see by the same sort of arguments that

δS

δx

j

= −m

j

¨x

j

− V

j

³

x

1

, · · · , x

n

´

(31)

where

−V

j

(x

1

, · · · , x

n

) ≡ −

∂

∂x

j

V (x

1

, · · · , x

n

) (32)

is the force on particle j. For S[x] to be an extremum, we must have (31) vanish for each j, which

just gives F = ma for each particle.

In general, if the Lagrangian depends on more degrees of freedom, Hamilton’s principle re-

quires that an Euler-Lagrange equation be satisﬁed for each coordinate:

∂

∂x

j

L

³

x, ˙x, t

´

−

d

dt

∂

∂ ˙x

j

L

³

x, ˙x, t

´

= 0 (33)

where the xs and ˙xs in the function L now indicate all the components — that is L(x, ˙x, t) is really

a shorthand for

L(x

1

, x

2

, · · · , ˙x

1

, ˙x

2

, · · · , t) (34)

Example - frictionless table

Here is an example of a Lagrangian for a system with two degrees of freedom. Consider a friction-

less table in the x-y plane with a hole at the origin. A mass m

1

slides on the surface of the table,

but it is attached to a massless string of length R which goes through the hole in the center of the

table and hangs straight down where it is attached to a mass m

2

. We can describe the conﬁguration

of the system by giving the length, `, of string on the table and the angle, θ, of the string on the

7

table from the x axis. From above, this looks like this:

.

..

.

...

.

m

1

.

..

.

..

.

`

.

◦

θ

.

8

From the side, it looks like

m

1

..

.

...

.

m

2

.

...............................................................

.

................................................................................................................................................................................................................................................................................................

.

The kinetic energy contains a term from the rate of change of `, proportional to the sum of

the masses (because both masses move when ` changes), and a term from the rate of change of θ,

proportional to m

1

—

T (`, θ,

˙

`,

˙

θ) =

1

2

(m

1

+ m

2

)

˙

`

2

+

1

2

m

1

`

2

˙

θ

2

(35)

9

.

...

.

..

.

..

.

..

.

`

.

..

.

˙

`

.

..

.

`

˙

θ

.

◦

θ

.

There there is also a potential energy related to the height of the mass m

2

,

U(`, θ,

˙

`,

˙

θ) = m

2

g` (36)

Now

L(`, θ,

˙

`,

˙

θ) =

1

2

(m

1

+ m

2

)

˙

`

2

+

1

2

m

1

`

2

˙

θ

2

− m

2

g` (37)

The Euler-Lagrange equations are

0 = m

1

`

˙

θ

2

− m

2

g −

d

dt

³

(m

1

+ m

2

)

˙

`

´

(38)

and

0 = −

d

dt

³

m

1

`

2

˙

θ

´

(39)

10

Generalized Force and Momentum

For a particle of mass m moving in a potential V (x), the Euler-Lagrange equation of motion can

be written as

dp

dt

=

d

dt

(m ˙x) =

d

dt

∂L

∂ ˙x

=

∂L

∂x

= −V

0

(x) = F (x) (40)

— the rate of change of the momentum is equal to the force. In the more general situation, this

suggests that we might regard the Euler-Lagrange equations,

d

dt

∂L

∂ ˙q

j

=

∂L

∂q

j

(41)

as a generalization of this — we call

∂L

∂ ˙q

j

(42)

the “generalized momentum” corresponding to the coordinate q

j

and

∂L

∂q

j

(43)

the “generalized force” corresponding to the coordinate q

j

. Then the Lagrange equation says that

the rate of change of the generalized momentum equals the corresponding generalized force.

A particularly interesting case occurs when the Lagrangian does not depend at all on some

coordinate q

j

. In that case, (41) implies that the generalized momentum corresponding to q

j

is

constant. This statement becomes even more interesting when you realize that we have great

freedom to choose the coordinates any way we want to. Thus if there is any coordinate system in

which the Lagrangian does not depend on some coordinate, then there is a conservation law — the

corresponding generalized momentum is conserved.

For example, in the mass on the frictionless table, the Lagrangian,

L(`, θ,

˙

`,

˙

θ) =

1

2

(m

1

+ m

2

)

˙

`

2

+

1

2

m

1

`

2

˙

θ

2

− m

2

g` (44)

doesn’t depend on θ. Thus the generalized momentum corresponding to θ,

∂L

∂

˙

θ

= m

1

`

2

˙

θ (45)

is constant. Of course, this is just what we found explicitly when we wrote down the Euler-

Lagrange equation, (21). Later, we will see that this conserved generalized momentum is angular

momentum about the origin, which is conserved because the system has a rotation symmetry about

the origin.

Reduced mass and center of mass

A nice example of using a change of coordinates to make a conservation law more obvious is the

use of relative and center-of-mass coordinates. This is a way of simplifying the analysis of systems

11

with two particles and a conserved momentum. It is sometimes useful, and later we will discuss

the extension to more particles, which is quite important.

Consider two particles interacting with one another through a potential that depends only on

the difference of the coordinates,

L(x

1

, x

2

, ˙x

1

, ˙x

2

) =

1

2

m

1

˙x

2

1

+

1

2

m

2

˙x

2

− V (x

1

− x

2

) (46)

We know that there is a conserved momentum in this system,

p = m

1

˙x

1

+ m

2

˙x

2

(47)

It is sometimes useful to change variables so that one of the variables is the combination that

appears in the potential,

x ≡ x

1

− x

2

(48)

and the other is related to the momentum

X ≡

m

1

x

1

+ m

2

x

2

m

1

+ m

2

(49)

This variable is called the center of mass. The connection with the momentum is that p is

˙

X times

the total mass of the system,

p = (m

1

+ m

2

)

˙

X (50)

Let us now see what the Lagrangian looks like in terms of x and X. We can do that by ﬁnding x

1

and x

2

in terms of x and X and inserting them into (46). Solving (48) and (49) for x

1

and x

2

gives

x

1

= X +

m

2

m

1

+ m

2

x x

2

= X −

m

1

m

1

+ m

2

x (51)

You can check that this works. Putting (51) into (46) gives

L(x, X, ˙x,

˙

X) =

1

2

(m

1

+ m

2

)

˙

X

2

+

1

2

µ ˙x

2

− V (x) (52)

where

µ =

m

1

m

2

m

1

+ m

2

(53)

is called the reduced mass. (52) has the form of the Lagrangian for a free particle (describing the

free motion of the center of mass) plus the Lagrangian for a single particle with the reduced mass

in the potential. This effectively reduces the problem with two degrees of freedom to a simpler

problem with one degree of freedom.

Energy again

Now we are going to do a little math that will lead to a remarkable and beautiful result. If the

Lagrangian does not explicitly depend on time, we will ﬁnd that we can construct a function of

the coordinates and the velocities of the system that does not change with time for any solution

12

Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

Подождите немного. Документ загружается.