Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

as the total kinetic energy long after the collision. At some intermediate time, when the particles

were close together, some kinetic energy was converted to potential, but it all comes back as the

particles separate. Thus, as long as one only asks about the initial and ﬁnal states, kinetic energy

is conserved. And of course, because Newton’s third law is satisﬁed, momentum is conserved at

all times, and in particular for the initial and ﬁnal states. This is a scattering process. We say that

the two particle have scattered from one another.

Now the point is that kinetic energy and momentum conservation put very strong constraints

on this process. Suppose that particle 1 has velocity ~v

1f

after the interaction and particle 2 has

velocity ~v

2f

.

Since the initial momentum and energy of particle 2 are zero, we can write:

m

1

~v

1i

= m

1

~v

1f

+ m

2

~v

2f

m

1

2

~v

2

1i

=

m

1

2

~v

2

1f

+

m

2

~v

2

2f

(8)

These constraints are very powerful. If you don’t know the mass of particle 2, for example, you can

calculate it from the three velocities. Scattering gives you information about the particles involved.

There is an interesting linguistic distinction that is made in calculations like this. We talk

about the features that follow from very general principles like conservation of kinetic energy and

momentum as the “kinematics” of the process. This is to be distinguished from the “dynamics”

of the process, which is everything else — in particular the details of the force law. At this point,

the distinction probably seems a little arbitrary, but in the next couple of weeks, as we begin to see

how general these conservations laws really are, this distinction will be more and more important.

Another place where the idea of scattering is crucial is in my own ﬁeld of particle physics. I

study particles that are very small. We can detect them, we can see their tracks, measure their

velocities, and energies and momenta, just as we would with a larger object. But they are so small,

that we cannot follow what happens when two of them collide in detail. We simply cannot measure

the forces involved in the tiny fraction of a second during which colliding subatomic particles are

in “contact” with one another.

1

What we do is scattering experiments, in which we measure the

initial energies and momenta of the particles before the collision, and then again after the collision.

Here, conservation of energy and momentum are really useful, because they put very strong limits

on what can happen. We will discuss this a bit now, and then in much more detail in a few weeks

when we discuss energy and momentum in relativity.

Elastic collisions

A familiar example of the use of kinematics is in elastic collisions of rigid bodies, like billiard

balls. The force in this case is certainly short-range, because it is only non-zero when the balls are

actually touching. “Elastic” is just a code word meaning that kinetic energy is conserved.

A famous and beautiful result that follows simply from conservation of kinetic energy and

momentum in an elastic collision is that if a moving particle with velocity ~v collides elastically

with a particle at rest with the same mass, the dot product of the velocities, ~v

1

and ~v

2

, of the two

particles in the ﬁnal state vanish, ~v

1

·~v

2

= 0. Thus either one of the two velocities vanishes, or else

the two velocity vectors are perpendicular to one another. This is very neat result, and it is easy to

1

In fact, the whole notion of these particles being in contact with one another is rather problematic. It is not clear

what it means.

4

prove using conservation of kinetic energy and momentum. Conservation of kinetic energy gives

1

2

m ~v

2

=

1

2

m ~v

2

1

+

1

2

m ~v

2

(9)

Conservation of momentum gives

m ~v = m ~v

1

+ m~v

2

(10)

Eliminating the ms and taking the dot product of each side of (10) with itself gives

~v

2

= (~v

1

+ ~v

2

) · (~v

1

+ ~v

2

) = ~v

2

1

+ ~v

2

+ 2~v

1

· ~v

2

(11)

Comparing this with (9) gives the desired result. No forces were ever mentioned. In fact, it does

not even matter here which of the two particles in the ﬁnal state was initially at rest and which was

moving. Since they have the same mass, it doesn’t matter.

Inelastic collisions

One of the hard parts of doing physics is ﬁguring out what principles to use in a particular prob-

lem. At some level, for example, we believe that energy and momentum are always conserved.

Sometimes, as in the example we just discussed, kinetic energy and momentum are obviously con-

served. But for example, when I take an egg and drop in on the ﬂoor, it is certainly not obvious.

Before it hits the ﬂoor, the egg has kinetic energy and momentum. After it hits the ﬂoor, it is just

a scrambled mess, sitting still, with no kinetic energy or momentum. What happened? Clearly the

problem with the eggs momentum is that the egg is not an isolated system. The ﬂoor pushed up on

the egg’s shell (and broke it), to change the eggs momentum. The problem with the egg’s energy

is that energy can get transformed from one form to another. In the process of breaking, the egg’s

parts actually heated up slightly, so slightly that we don’t notice it, but enough so that energy is

conserved.

Frequently, we are interested in collisions in which momentum is conserved, but kinetic energy

is not. These are called “inelastic” collisions. The classic inelastic collision is two lumps of clay

hitting and sticking. If the two lumps have masses m

1

and m

2

with velocities v

1

and v

2

respectively,

the ﬁnal momentum is

m

1

~v

1

+ m

2

~v

2

(12)

We can now compute the ﬁnal velocity of the system by dividing by the total mass,

~v

ﬁnal

=

m

1

~v

1

+ m

2

~v

2

m

1

+ m

2

(13)

The unspoken assumption behind (13) is the common sense statement that mass is conserved, like

energy and momentum — that the mass of the system of two lumps stuck together is just the sum

of the masses of the two lumps. This is very reasonable, and it is consistent with what each of

knows in our bones about the world. However, it is wrong. We will see in a few weeks that when

particles collides at speeds close to the speed of light, conservation of mass may be completely

wrong. Nevertheless, it is a very good approximation as long as none of the particles are moving

at close to the speed of light, and since light travels so rapidly, this is not much of a restriction.

5

The speed of a bullet

There is a classic physics demonstration in which one shoots a bullet into a block on wood which is

the bob of a pendulum. By measuring the distance h the pendulum bob goes up, the mass M of the

bob and the mass m bullet, you can infer the initial speed v of the bullet. I like this as an example

of the use of conservation of energy and momentum because for this system, neither momentum,

nor kinetic plus potential energy are actually conserved. Nevertheless, if you keep your wits about

you, you can use conservation of energy and momentum to solve the problem.

.

......................................................................................................

.

.......................................................................................................

.

M

.

............................

.

............................

.

← v

m

.

............. ............. ............. ............. .

.

.....................................................

.

......................................................................................................

.

.......................................................................................................

.

M + m

.......................................................................................................................................................

.

..

.

..

.

h

.

The analysis is deceptively simple. The initial momentum of the bullet is mv. If the bullet stops

relatively quickly in the block of wood, it will still be moving almost horizontally when the bullet

stops. Because there is no horizontal force on the bullet-bob system, the horizontal component of

the momentum is also mv to a very good approximation. Thus after the bullet has come to rest

inside the bob, the velocity and the kinetic energy of the bob+bullet system is

V =

mv

M + m

E =

1

2

(M + m)V

2

=

1

2

m

2

v

2

M + m

(14)

6

This is much smaller than the initial kinetic energy of the bullet, by a factor of m/(M + m). Most

of the energy is lost to friction. But after the bullet comes to rest with respect to the bob, no more

frictional forces operate, and energy is conserved. The kinetic energy in (14) is converted into

potential energy at the bob rises, and the maximum height thus satisﬁes

1

2

m

2

v

2

M + m

= (M + m)gh or v =

M + m

m

q

2gh (15)

More elastic collisions and a dangerous demo

Let’s end with another example of an “elastic” collision in which the total kinetic energy of the ob-

jects involved is conserved. Then the kinematic constraints of energy and momentum conservation

apply. Here is an example that makes an amusing demo. Two elastic balls with different masses

are dropped on the ﬂoor as shown:

...

.

..

....

.

..

.

..

.

..

.

..

.

..

.

m

M

v

0

v

0

The way to do this one is to think of it in stages, imagining that the balls are just slightly separated.

Then the big one hits ﬁrst, and because of conservation of momentum and energy, just reverses

direction:

..

.

..

....

.

..

.

..

.

..

.

..

.

..

.

m

M

v

0

v

0

Then in the next stage, the two balls scatter:

...

.

..

......

.

...

..

.

..

.

..

.

..

.

m

M

V

f

v

f

7

Then conservation of energy and momentum gives

Mv

0

− mv

0

= MV

f

+ mv

f

Mv

2

0

+ mv

2

0

= MV

2

f

+ mv

2

f

(16)

We could solve these two equations by solving the ﬁrst for V

f

and inserting it into the second,

which then becomes a disgusting quadratic equation for v

f

. Instead, let’s mess around a bit. First

rewrite (16) as

M(v

0

− V

f

) = m(v

0

+ v

f

) (17)

and

M(v

2

0

− V

2

f

) = m(v

2

f

− v

2

0

) ⇒ M(v

0

− V

f

)(v

0

+ V

f

) = m(v

f

+ v

0

)(v

f

− v

0

) (18)

In the actual physical situation of interest, the two sides of (17) do not vanish (because, for example,

v

0

and v

f

obviously have the same sign). Thus we can divide (18) by (17) to get the much simpler

equation

v

0

+ V

f

= v

f

− v

0

(19)

Multiplying this by M and adding to (17) to eliminate V

f

, we get

2Mv

0

= (M + m)v

f

+ (m − M)v

0

⇒ (3M − m)v

0

= (M + m)v

f

(20)

Thus the solution for v

f

that we are interested in is

v

f

=

3M − m

M + m

v

0

(21)

Thus if M À m, the light ball on top ends up with nearly three times its initial velocity and nearly

nine times its initial kinetic energy.

We can illustrate this with a basketball and a baseball, but we have to be careful.

8

lecture 6

Topics:

F = ma → Euler-Lagrange equations

Hamilton’s principle

Functions of functions

Calculus of variations

Functional derivatives

Finding functional derivatives

Back to Hamilton’s principle

More degrees of freedom

The Lagrangian and the action

Quantum mechanics and the classical trajectory

Appendix: On the functional Taylor series

F = ma → Euler-Lagrange equations

This week, we will introduce some difﬁcult, but beautiful material - Lagrangian mechanics. Essen-

tially, having spent the last couple of weeks getting a better understanding of classical mechanics in

terms of second order differential equations, we are now going to introduce a completely different

formulation of mechanics based on the calculus of an inﬁnite number of variables! This proba-

bly sounds really scary. But DON’T PANIC! I am introducing this for several reasons. I think

that you will ﬁnd it fascinating, and I hope that it will give you a different philosophical slant on

classical mechanics. It may also give you a hint about how the quantum mechanical nature of the

world may determine the shape of the classical mechanics that we are used to. The mathematics

will sound unfamiliar to almost all of you. But in the end, we will not actually be doing anything

with it that you do not already know how to do. Finally, it is really useful — not just theoretically

but also for solving real problems.

The result of the painful analysis I am about to subject you is actually pretty simple. The

statement is this. To solve many classical problems (and we will discuss later why this works in

the most interesting cases) you construct a function (called the Lagrangian) which is the kinetic

energy T minus the potential energy V as a function of the coordinates and their time derivatives

(the velocities).

L

³

q, ˙q

´

T

³

q, ˙q

´

− V

³

q, ˙q

´

(1)

(T and V may not depend on both q and ˙q, but that will depend on the problem). Then for each

coordinate, you get an equation of motion as follows:

d

dt

Ã

∂

∂ ˙q

L

³

q, ˙q

´

!

=

∂

∂q

L

³

q, ˙q

´

(2)

This gives you a set of straightforward rules that will allow you to write down the second order

differential equations for the time evolution of a physical system in a single step, without identiﬁng

all the separate forces acting on the system. So I hope that even if you never fully appreciate all

the deep philosophical implications of the Lagrangian approach, you will love it as a labor-saving

device.

1

I could of course just write down (1) and skip all the difﬁcult math that leads up to it, because

the hard stuff won’t really be important in the way we use these results most of the time. I think

it is good to go through it once, but really what I am really most interested in is the philosophical

implications of all this. The deeper question that we are heading to is Why are energy and

momentum conserved? Next week, I will try to convince you that these conservation laws follow

directly from fundamental symmetries of the world plus the assumption that the laws of mechanics

arise from a Lagrangian by the simple set of rules you will learn today. This will move us quite a

way along in our quest to understand the fundamental meaning of classical mechanics.

Hamilton’s principle

We will start by showing in what sense Newton’s laws can be formulated in a way that appears very

different, not as a differential equation, but as a condition that picks out the classical trajectory of

a particle by comparing with all other motions the particle might have had! This probably sounds

pretty wierd. Later we will argue that this new formulation is actually much deeper and more

fundamental. It is also a gorgeous piece of mathematics. So hold on to your hats, and remember

that it is not going to be as complicated as it seems at ﬁrst.

Consider the one dimensional motion of a particle with coordinate x in a potential V (x). Call

the particle’s kinetic energy

T ( ˙x) =

m

2

˙x

2

(3)

Now we would like to ﬁnd a particular trajectory x(t) are such that the particle moves from x

1

at

time t

1

to x

2

at time t

2

— or

x(t

1

) = x

1

x(t

2

) = x

2

(4)

Hamilton’s principle is the statement that if you compute the quantity S[x] (called the action —

I’m not really sure why)

S[x] ≡

Z

t

2

t

1

dt

·

T

³

˙x(t)

´

− V

³

x(t)

´

¸

(5)

depending on a function x(t) satisfying

1

then the variation of S[x] with respect to the function

x(t) vanishes for the actual trajectory. The hard part of Hamilton’s principle will not be proving

this statement, but ﬁguring out exactly what it means to talk about the variation of something with

respect to a function.

The ﬁrst thing to notice is that T − V is an ordinary function of two variables, x and ˙x,

2

but

that S[x] is actually a function of a function — it depends on x (t) for all values of t from t

1

to t

2

1

We will see later that the restriction to functions satisfying (4) is important and has to do with the initial conditions

that we have spent so much time talking about in the ﬁrst couple of weeks.

2

In the simple example we are working out now, T is a function of one of them and V of the other, but in general,

both T and V could depend on both x and ˙x.

2

where x(t) can be any function satisfying (4) — something like

x

1

x

2

t

1

t

2

.

..

....

.

..

......

.

x(t)

Thus S[x] is a function whose argument is itself a function (such an object is sometimes called a

functional and I may sometimes use that term). I have put the x in square brackets to remind you

that in this case x is a function rather than a number. The value of S[x], on the other hand, is just

a number. It doesn’t depend on t. The variable t in (5) is a dummy variable. Now Hamilton’s

principle is a statement about the variation of S[x] as we let x(t) vary over all possible functions

satisfying (4).

3

We will ﬁnd that when x(t) is very near to a solution to Newton’s second law, then

S[x] changes slowly as a function of whatever parameters you use to specify the function x(t).

When x(t) is a solution, S[x] is not varying at all.

Functions of functions

I imagine that the idea of a functional — that is a function of a function — is pretty unfamiliar to

most of you, but you shouldn’t get too worried about it. Most of you have learned or are beginning

to learn about the calculus of functions of several variables, and dealing with functionals is not

really much different. The main differences are in notation. In fact, I would argue that the big jump

is going from one or two variables to more than that. Once you have made it to three variables, it

really doesn’t get any harder to think about more — not even an inﬁnite number more.

Here is what I mean by the peculiar statement that going from two variables to three variables

is what is hard. This has to do with visualization. As you have probably noticed, it gets harder to

make a mental picture of what a function means as the number of variables increase. A function

of a single variable is easy. We naturally associate a function f(x) with a graph of y = f(x).

This allows us to do things that bring the function alive to us, such as relating the derivative of the

function to the slope of the line in the graph. We can sort of do something similar with a function

of two variables f(x, y) by imagining a surface in three dimensional space with z = f(x, y). This

3

Really? All possible functions? One has to be reasonable here — it might be better to say all possible functions

for which the integral in (5) makes sense — differentiable functions in this example. We will ignore such issues and

leave them for the mathematicians.

3

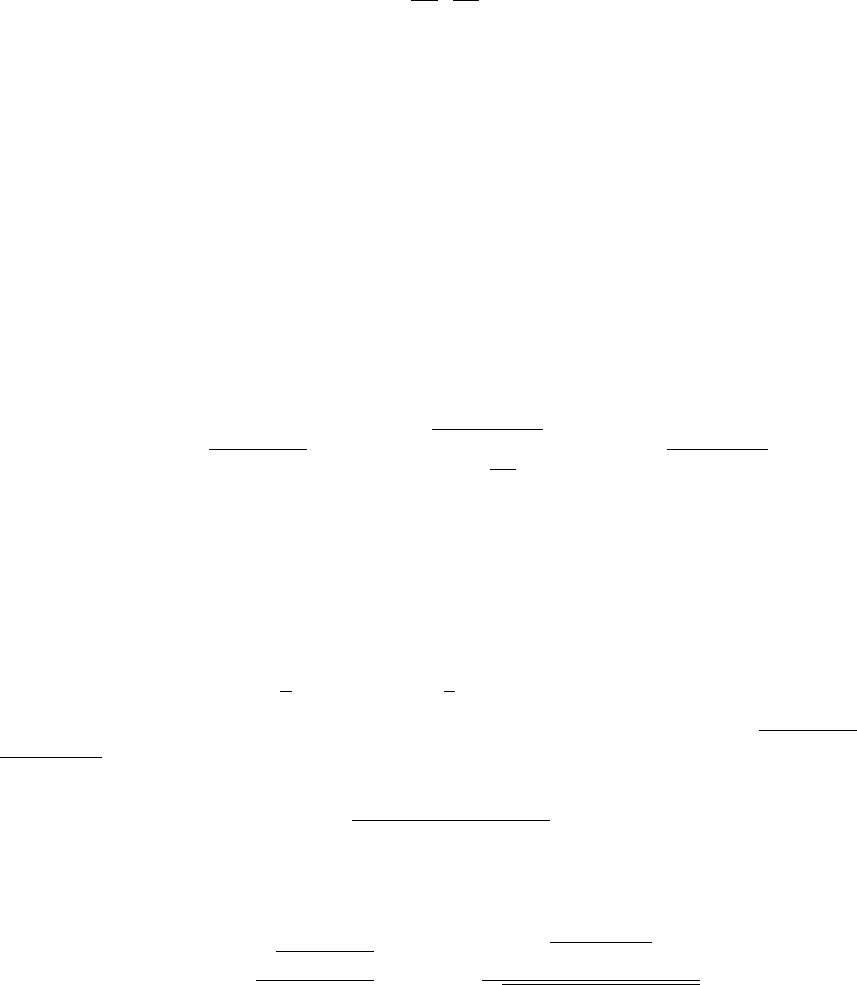
can be quite helpful, because it allows you to have a visual representation of features that only

appear with more than one variable, such as the gradiant vector, which for two variables x and y

looks like the two dimensional vector

~

∇ =

Ã

∂

∂x

,

∂

∂y

!

(6)

The vector

~

∇f(x, y) points in a direction that corresponds to going upwards on the surface z =

f(x, y).

But what do you do about visualizing functions of three variables, or more? There is really no

ideal way of doing this. So already by the time you get to functions of three variables, you have to

stop relying on visual crutches and just develop an analytic sense of what the function means.

A functional like S[x] is just a function of an inﬁnite number of variables where the variables

are the values of x(t) at all possible values of t. The really peculiar new thing about a functional is

that the variables are labeled by a continuous parameter, rather than having different names like x,

y and z, or different discrete indices, like a

1

, a

2

, etc. This is why functionals look so different and

why we have to invent some new notation to deal with them.

A mathematical example of a functional is the length of a path described by a curve, y = f (x).

The path length from x

1

to x

2

is

P [f] =

Z

x

2

x

1

q

dx

2

+ dy

2

=

Z

x

2

x

1

dx

v

u

t

1 +

Ã

dy

dx

!

2

=

Z

x

2

x

1

dx

q

1 + f

0

(x)

2

(7)

The path length depends on the function f that deﬁnes the shape of the curve. This example is

particularly interesting because it depends on the endpoints in same way that (5) does.

Here is a more physical example. Suppose that the function y = f(x) in (7) describes the

height of the track of of roller coaster. If a roller car is moving along the track with mass m and

energy

E =

1

2

mv

2

+ mgy =

1

2

mv

2

+ mg f(x) (8)

the time the car takes to get from x to x + dx is the inﬁnitesimal path length,

√

dx

2

+ dy

2

=

dx

q

1 + f

0

(x)

2

divided by the speed v which from (8) is

v =

r

2

³

E − mg f(x)

´

/m (9)

Thus the time the car takes to get from x

1

to x

2

is

τ[f] =

Z

x

2

x

1

√

dx

2

+ dy

2

v

=

Z

x

2

x

1

dx

q

1 + f

0

(x)

2

r

2

³

E − mg f(x)

´

/m

(10)

The time (10) is a function of E, m and g, but it is a functional of the function f(x) that describes

the height of the track. This is an important example to understand and we will try to come back

to it several times over the next few weeks.

4

Calculus of variations

Now let’s return to Hamilton’s principle. The proof and indeed the more precise mathematical

statement of the principle is an exercise in what is called the calculus of variations, which is sort of

calculus with an inﬁnite number of variables. It probably won’t surprise you that what we need to

do is to generalize the notion of a derivative to functionals and to explore the nature of the Taylor

series. After all, these are our main tools in understanding how things vary.

The actual example we are interested in is complicated because the integrand on the right hand

side of (5) depends on both x(t) and ˙x(t), so let us ﬁrst discuss a couple of simpler examples.

Consider the quantity

W [x] =

Z

t

2

t

1

dt

³

x(t) − t

´

2

(11)

and ﬁnd the value of x(t) for which the variation of W [x] with respect to x(t) vanishes. We can do

this by the following trick. Suppose that we have already found the soltuion x(t). Now consider

small variations about this particular function:

x(t) + δx(t) (12)

I’ve used the symbol δ rather than ∆ just to remind us that this is a “small” function rather than a

small number. Now look at (11) as function of x + δx,

W [x + δx] =

Z

t

2

t

1

dt

³

x(t) + δx(t) − t

´

2

=

Z

t

2

t

1

dt

³

x(t) − t

´

2

+

Z

t

2

t

1

dt δx(t) 2

³

x(t) − t

´

+

Z

t

2

t

1

dt

³

δx(t)

´

2

= W [x] +

Z

t

2

t

1

dt δx(t) 2

³

x(t) − t

´

+ O (δx

2

)

(13)

Now we look at the coefﬁcient of the linear term in δx(t), which is 2

³

x(t) −t

´

. This vanishes for

all possible small functions δx(t) if

x(t) = t (14)

and this is the answer we are looking for. Around the function x(t) = t, there is no linear term in

the expansion of W[x]. Note that while t in (13) is a dummy variable, we can say something about

the t dependence because we require that the variation vanishes for any possible δx(t). We will

come back to this below when discuss functional derivatives.

This result is quite reasonable and maybe obvious in this particular example because W [x] is

actually minimized for x(t) = t. The variation of a functional at a minimum vanishes for the

same reason that the derivative of a smooth function vanishes at a minimum. If there were a

linear variation, then on one side or the other, the result would be larger, which is impossible at a

minimum value. But what we want to extract from this calculation is not the result, but the general

technique.

Functional derivatives

What we did to solve the variational problem for (11) was to set to zero the coefﬁcient of the linear

term in δx(t) in W [x + δx]. It is useful to give this coefﬁcient a name, so we call it a functional

5

Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

Подождите немного. Документ загружается.