Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

Подождите немного. Документ загружается.

is just the statement that such a function exists. Since it exists, we can give it a name G and write

the statement A in mathematics as

A ⇔ x(t) = G

, v

, t

(12)

Furthermore, because we can specify x and ˙x at any time we choose. We can use any t

in (12)

and get the same trajectory so long as we take x

and v

to be the values of the position and the

velocity on that trajectory at the time t

. This function G contains everything about all possible

motions of the system!

The mild assumption we need to get F = ma from this is a smoothness assumption. We must

assume we can differentiate our function x(t) with respect to time. Obviously, if we can’t do this,

we have no hope of getting to Newton. This assumption is really very mild.

Now here is the basic idea. Because of the meaning of the initial conditions, we can put

= x(t

) and v

= ˙x(t

) into (12) and rewrite it as

x(t) = G

x(t

), ˙x(t

), t

, t

(13)

This is a peculiar equation, because the trajectory x(t) appears on both sides, on one side inside

the function G. Because of this, the equation is telling us something about the function x that

describes the trajectory. It is still more complicated than it has to be though, because it involves

two different times, t and t

. But the other peculiar thing is that the right hand side of (13) must be

completely independent of t

, because t

doesn’t appear on the left had side at all. We can use this

to get information on the trajectory that only depends on a single time. In particular, now we can

start differentiating both sides of the equation with respect to t and afterwards, setting t

equal to

t to get an equation that only depends on the the trajectory and its derivatives at a single time. We

will see that differentiating zero or one time doesn’t give us anything interesting - just tautologies.

But differentiating twice is interesting.

So here goes. First we set t

→ t in (13).

x(t) = G

x(t), ˙x(t ), t, t

(14)

This is a tautology, because we can use the time t as the initial time to specify the trajectory, and

this just says that the particle is where it is supposed to be at time t. To put it another way, if I

change all the ts to t

in (14),

x(t

) = G

x(t

), ˙x(t

), t

, t

= G

x(t

), ˙x(t

), t

, t

t=t

= x(t)|

t=t

(15)

this is just the statement of the initial condition for x(t

Likewise, differentiating once with respect to t gives us nothing new.

˙x(t) =

∂

∂t

x(t

), ˙x(t

), t

, t

∂

∂t

x(t

), ˙x(t

), t

, t

(16)

Again we can set t

→ t because the left hand side doesn’t depend on t

. The equation (16) just

says that the particle is going as fast as it should be going at time t.

˙x(t

) =

∂

∂t

x(t

), ˙x(t

), t

, t

∂

∂t

x(t

), ˙x( t

), t

, t

t=t

∂

∂t

x(t)|

t=t

(17)

But differentiating twice with respect to t gives us a second order differential equation that the

trajectory must satisfy. And this is Newton’s second law.

¨x(t) =

∂

∂t

x(t

), ˙x(t

), t

, t

∂

∂t

x(t

), ˙x(t

), t

, t

(18)

The right hand side of (18) is just some function of x(t), ˙x(t) and t. Thus as promised, is a second

order differential equation for x(t). This is just F = ma with

F (x(t), ˙x(t), t) = m

∂

∂t

x(t

), ˙x(t

), t

, t

(19)

From the function that is the mathematical description of the assumption A that the trajectory is

determined by an initial position and velocity, we can ﬁnd the force that makes F = ma work.

So what?

What have we really learned from this mathematical philosophy? We have shown that Newton’s

second law is actually equivalent to assumption A — each implies the other. Of course, we haven’t

really understood why F is equal to ma, because we still don’t know why assumption A is true.

Must it be true? Actually, I don’t think so. In fact, I don’t really think it is true. Like most of the

things we teach as “physical laws”, it is only an approximation to what is really going on. We will

come back to this much later. But this is a nice example of the kind of thinking that we will be

doing a lot of in this course.

Should you take Physics 16?

Because this is the ﬁrst day of classes, you are all full of adrenaline and are paying close attention

to every word I say. But normally, at about this point in an 1.5 hour lecture, you would all be

falling asleep and would need a little something to perk you up. This is where we normally put

a miniexam, a small problem that you work on with a random group of other students. Since we

haven’t done enough yet to warrant a miniexam, I thought that instead, I would say a bit about the

course, and then see whether you have any questions. There is a lot more detailed information on

the information sheet on the web page, so please read that carefully.

Presumably you are all here because you have good preparation in physics and math and you

are afraid that Physics 15a would be boring. The ﬁrst thing to say is that Physics 15a would

probably not be boring. It is a good rigorous course, and almost all of you would learn something.

However, for many of you, Physics 16 may be more fun, because I will spend a lot less time on

statics, assuming you already know about adding up vector forces and torques on objects that are

not moving. I will also spend a bit less time trying to nail down the connection between physics

and calculus, assuming that you are all pretty well started along that path. This will allow me more

time to indulge in ﬂights of theoretical fancy, such as trying to understand why F is equal to m a.

You should consider 16 if this appeals to you.

I would make one request. Don’t take 16 because you think that it is going to be hard for you

and you want a challenge. And don’t drop it because you think it is going to be hard for you and

you don’t want a challenge. In fact, Physics 16 is in many ways a very humane course. We will

do civilized things like having a take-home component of our exams so that we can correct for

problems that some people have with time pressure on exams. And while the material is hard,

as long as you get the help that we are eager to give you, the work is really not very different

from that in 15a. For some of you it may take a little more time, so as I say at the end of the

information sheet, it is important to think about it in the context of your whole schedule, curricular

and extracurricular.

Finding trajectories numerically

If you are given a complicated force law, depending (for one degree of freedom) on x, ˙x and t, you

will usually not be able to solve for the trajectories in terms of known functions. However, you

can always ﬁnd them by brute force, solving F = ma numerically. One simple way to do this is

to make small time steps and use the most important formula in Physics — the Taylor expansion.

Suppose that you are given the initial conditions, x(t

) and ˙x(t

). Then you can ﬁnd x and ˙x

approximately for a slightly later time, t

+ ∆t, by Taylor expanding the function x(t

+ ∆t)

around t

. The Taylor expansion looks like this:

x(t

+ ∆t) = x(t

) + ∆t ˙x(t

) + · · · (20)

where the · · · are terms with more powers of ∆t. I love the Taylor expansion, and we are going

to come back to it many times in the course, and later we will talk about the higher order term.

But here, these can be ignored if ∆t is sufﬁciently small. This ﬁrst term in the Taylor expansion is

nothing more than the deﬁnition of the derivative:

x(t

+ ∆t) = x(t

) + ∆t ˙x(t

) + · · · ⇔ ˙x(t

) =

x(t

+ ∆t) − x(t

)

∆t

+ · · · (21)

How does this help us ﬁnd x(t). This is ﬁne as far as it goes, because we are given the initial

conditions for x(t

) and ˙x(t

). But what we would like to do is to be able to iterate this procedure

and ﬁnd x(t

+ n∆t) which would mean that we could ﬁnd x(t) (at least approximately) at a

whole sequence of future times. And in the next step we have a problem because we don’t know

˙x(t

+ ∆t) from the initial conditions. But now the key point is that we can also keep track of ˙x

˙x(t

+ ∆t) = ˙x(t

) + ∆t ¨x(t

) + · · · (22)

And we know ¨x(t

) from F = ma:

¨x(t

) = a(t

) =

F (x(t

), ˙x( t

), t

) (23)

You can always do this for F = m a. Given x and ˙x at some time t

, you can always ﬁnd x

and ˙x for an inﬁnitesimally later time, t

+ ∆t.

Now that you know x and ˙x for the later time t

+∆t, you can apply exactly the same procedure

again and compute them for t

+ 2∆t.

Then do it again and get x and ˙x for t

+ 3∆t.

And so on!

This kind of iterative procedure is ideal for a computer — the computer just has to do the

same things over and over again to construct the approximate trajectory. And if you want your

approximation to be more accurate, you just have to make ∆ t smaller, so that the · · · that you

throw away in (20) and (22) are smaller. If you are doing this on a computer, it doesn’t matter how

complicated the function F is.

But sometimes, it is nice to have analytic expressions for the trajectories. You may be able

to ﬁnd such things if the force is a simple enough function. For the rest of this lecture and on

Thursday, we will give examples in which this can be done, both in general, using integration, and

in speciﬁc cases where the integrals can be done analytically.

Meanwhile, notice that the analysis we have just given really is a “physicist’s proof” of the

statement that a second order differential equation has a solution that is ﬁxed when we know q and

˙q at some time. We have “proved” this by actually constructing the solution! This is the best kind

of proof for a physicist — one that not only tells you that the solution exists, but actually shows

you how to ﬁnd it. Of course this would never satisfy a mathematician — too many loose ends?

But note that we can “prove” the general theorem this way — that an n-th order differential

equation requires n initial conditions. Because our original equation was a second order differential

equation, we had to keep track of both x(t) and ˙x (t) while we take our small time steps. In a ﬁrst

order differential equation, we would only have had to keep track of x(t), because the differential

equation would tell us ˙x(t) directly in terms of x(t). Then we need only one initial condition. In

a third order differential equation, we would have to keep track of x(t), ˙x(t) and ¨x(t), because the

differential equation only tells us the third derivative. Then we would need three initial conditions.

And so on.

Forces of the form F (t)

The big general principle of mechanics that we have talked about today is that we need two initial

conditions per degree of freedom to specify how a system moves. Staple this in your brains. This

is something we will come back to and will try to understand better. But now and next time we

will spend a bit of time discussing some examples of the different ways these initial conditions can

appear. There are more in Chapter 2 of Dave Morin’s book.

The simplest and least interesting example of a force law in which the trajectories can be found

formally using integration is a force depending only on t, not on x or ˙x. In this case, we can simply

use the fundamental theorem of integral calculus. The acceleration is the time derivative of the

velocity, so we can write F = ma in this case as

a(t) =

v(t) =

F (t) (24)

The fundamental theorem tells us that the general solution to (24) can be written as

v(t) =

F (t

) + constant (25)

There are a number of things to note about (25):

Note that t

here is a dummy variable. We will discuss dummy variables in more detail below, but there is a

possible notational confusion. The symbol t

does not mean “the derivative of t” but is just a symbol for a new

independent variable. We could have called it s instead, but Dave’s book uses the t

notation in this way, so I am trying

to do it in lecture as well. You will have keep your wits about you to ﬁgure out what is going on, but you can almost

always tell from the context. If a

appears on a function, it is a derivative. If the

appears on a variable, it is a new

variable. Thus f

(x) means the derivative with respect to x of the function f (x), but f (x

) means the function f of

the variable x

and f

) means the derivative with respect to the variable x

of the function f(x

1. We can easily verify that it works, because if we differentiate the left hand side with re-

spect to t, we just get the acceleration, a(t). On the right hand side, integral calculus tells

us that differentiating the integral with respect to t gives the integrand evaluated at t, and

differentiating the constant gives zero, so we get

a(t) =

F (t) (26)

which is F = ma.

2. We need to invent a new symbol for the argument of the integrand, because the previous

argument only works if the time dependence appears only as the upper limit of the integral,

so we have just put a prime on t. The dt

in (25) identiﬁes the variable t

as a completely

independent “dummy” variable. It is a “dummy” because in the expression (25), it doesn’t

have any particular value. It is just a symbol to indicate exactly what integral we are doing.

This is simple but important. You should never ever write an equation like

A(t) =

dt B(t) (27)

Because the variable t in (27) appears in two ways — as a real variable and as a dummy

variable — and it can’t be both. Thus (27) doesn’t mean anything at all, and if we see it

on one of your problem sets or tests we will deal sternly with it!

Also, the integral

B(t) (28)

is not the same as

B(t

) . (29)

Both of these expressions are sensible, they are just not the same. In fact, we can do the ﬁrst

integral explicity because the integrand B(t) doesn’t depend on the integration variable, the

dummy variable t

B(t) = (t − t

) B(t) . (30)

3. The integral needs some lower limit, and we have called this t

, expecting it to have some-

thing to do with the initial conditions.

4. Finally, (25) appears to depend on both t

and the unknown constant. But we can determine

the constant by just setting t = t

, which gives

v(t

) =

F (t

) + constant (31)

The integral vanishes here because the range of integration is zero, so we know that

constant = v(t

) = ˙x(t

) . (32)

We sometimes call the initial condition ˙x(t

) an integration constant because of the way it

appears in (31).

Putting (32) back into (25) gives the ﬁnal result for the velocity,

v(t) =

F (t

) + v(t

) (33)

Another way to think about the result (33) is from the following chain (really just going back-

wards through the same argument):

F (t

) =

a(t

) =

v(t

) = v(t) − v(t

) (34)

which is equivalent to (33).

Now that we know v(t) as a function of t (at least formally, in terms of an integral), we can

ﬁnd x(t) by just repeating the procedure. But v is the time derivative of x, we can write

x(t) =

v(t

) + x(t

) (35)

where again, the initial condition appears as an integration constant. Then we can put (33) into

(35) to get

x(t) =

F (t

) + v(t

)

+ x(t

) (36)

Note the new variable of integration, again to keep from getting the integration variable confused

with the range of integration. Finally, we can do the integral for the term proportional to v(t

because it is just a constant, and get the result

x(t) =

F (t

) + v(t

)(t − t

) + x(t

) (37)

The terms in (37) are easy to understand. The last term is where the object started — the initial

condition for the position. The middle term describes motion with constant velocity v(t

), which

is what the object would be doing if there were no force on it. And the ﬁrst term is the effect of

the force. Notice that (37) is valid for a constant force F (t) = F

(a constant is just a particularly

simple function of t). And sure enough, we can do the integral in that case and get (11).

x(t) =

F (t

) + v(t

)(t − t

) + x(t

)

+ v(t

)(t − t

) + x(t

)

− t

) + v(t

)(t − t

) + x(t

)

(t − t

)

+ v(t

)(t − t

) + x(t

)

(38)

lecture 2

Topics:

Where are we?

Forces of the form F(v)

Example: F (v) = −m Γ v

Another example: F (v) = −m β v

Forces of the form F(x)

Review of the harmonic oscillator

Linearity and Time Translation Invariance

Back to F (v) = −m Γ v

Where are we?

Last time, we discussed Newton’s second law — F = ma. I tried to convince you that this is

essentially equivalent to the statement that the motion of any given classical mechanical system

is determined by a set of initial conditions, the values of the coordinates which specify its con-

ﬁguration, and their ﬁrst derivatives at any given time. I also suggested that this is a very deep

and interesting fact about the world, and promised that we would come back to it at the end of the

course and give at least a provisional explanation of it.

We also discussed how to solve for the motion of a system numerically by keeping track of q

and ˙q as functions of time, and using the Taylor expansion and F = ma to calculate approximately

how they change in a small time step ∆t. By putting together many small time steps, we can trace

out the trajectory of the system. This procedure works for any any number of degrees of freedom,

and it should convince you that in principle, giving a second order differential equation for the

conﬁguration of a classical does just what expect - it determines the trajectory in terms a set of two

initial conditions per degree of freedom.

In a sense, our numerical analysis completely solves the problem - at least least your computer

can construct the solution to any problem. But for us people, it is nice to have analytic solutions that

we can use to develop our intuition. So we also talked about systems with one degree of freedom

in which the force depends only on time. In this VERY special case, we found that we could write

down the formal solution simply by integration. Then if the integral can be done analytically, we

get a completely analytic solution.

Today, we will give some more examples of very special systems in which we can do more

than just solving numerically. In some sense, I will just be showing you a collection of dirty tricks,

because it is only in very special cases that they work. But more generally, today’s lecture should

be regarded as a bunch of examples of the different ways in which initial conditions can enter into

the solutions of classical mechanics problems. We always need two initial conditions per degree

of freedom. But they appear in the actual trajectories in many different ways. In fact, I have

something else in mind as well. At the end, when we come to discuss the harmonic oscillator, we

will see that there are some very important general principles at work. These will be very useful,

and we will come back to them many times.

Forces of the form F (v)

Formally, it is almost as easy to solve for the trajectory for a system of one degree of freedom

in which the force depends only on v as for a force that depends only on t. For a force F (v)

depending only on v, we write F = ma as

= F (v) (1)

We can rewrite this as

dt = dt

F (v)

(2)

which we can simplify just by integration. Again we have to remember that the integration vari-

ables must be distinguished from the ranges of integration. Again I will use the notation in Morin’s

book and just put primes on them. Putting in all the steps very formally, we get

= t − t

F (v

)

v(t)

v(t

)

F (v

)

(3)

The last step is a change of variable in the integration from t

to v

= v(t

). A quick and dirty way

of getting to (3) is to write

dt =

F (v)

dv (4)

and integrate both sides.

This is a perfectly good way of looking at it. The equation (4) describes

how a small change in t is related to the small change in v that takes place during the small change

in t. Integration adds the small changes up.

Equation (3) implicitly determines v(t) in terms of t − t

and the initial condition v(t

). And

once we know v(t), we can integrate to get the trajectory x(t) (using the initial condition x(t

) as

usual).

Let’s see how this works in an important example, describing a frictional force.

Example: F (v) = −β v = −m Γ v

If an object moves very slowly through a thick gas or a liquid, there is almost always a frictional

force approximately proportional to the velocity (and in the opposite direction). What “slowly”

means depends on the size of the object and the viscosity of the stuff it is moving through. We will

come back later in the lecture to why this force should exist. For now, let’s see how (3) works for

such force, which we can take to have the form

F (v) = −β v = −m Γ v (5)

(3) becomes

= −

v(t)

v(t

)

Γ v

(6)

When we do that, we must turn them into dummy variables, which we do, as usual, by putting primes on the.

The factor of m is just there to make the units of the constant Γ simpler. It makes the ms cancel in (3). Physically,

the factor doesn’t really make any sense, because the frictional force on an object just depends on its size, shape and

surface properties — not on its mass. But of course the essential physics doesn’t change when you leave out the m

and write things in terms of β - the formulas just look a bit more complicated.

This looks nicer if we put the Γ on the other side

= −

v(t)

v(t

)

(7)

Γ (t − t

) = −ln v(t) + ln v(t

) (8)

ln v(t) = ln v(t

) − Γ (t − t

) (9)

ln v(t)

= e

ln v(t

)−Γ (t−t

)

(10)

v(t) = v(t

) e

−Γ (t−t

)

(11)

This makes sense. The constant Γ has units of 1/T , so the exponent is dimensionless, as it should

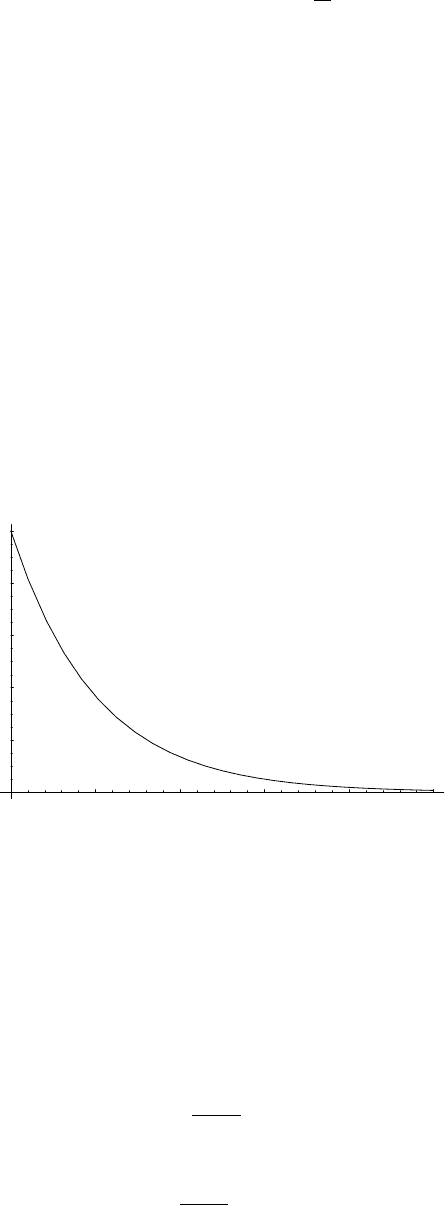
be. Thus the units work in (11). We can also check this in the limit Γ → 0. In this limit, where

the frictional force disappears, the velocity goes to a constant, as it should. For nonzero Γ, the

frictional force causes the velocity to gradually drop off. Because the force is proportional to v,

the drop-off gets slower and slower as the velocity gets smaller, in this case, exponentially. A plot

of the velocity (in units of v

) as a function of time (in units of 1/Γ) has an exponential shape that

I hope is familiar:

2 3

4 5

0.2

0.4

0.6

0.8

Now let’s compute x(t) by integrating (11).

x(t) = x(t

) +

v(t

) = x(t

) +

v(t

) e

−Γ (t

−t

)

(12)

Doing the integral is easier if we substitute

u = e

−Γ (t

−t

)

du = −dt

Γ e

−Γ (t

−t

)

(13)

we get

x(t) = x(t

) −

v(t

)

−Γ (t−t

)

du (14)

which gives

x(t) = x(t

) +

v(t

)

1 − e

−Γ (t−t

)

(15)

Note that the object moves a ﬁnite distance, v(t

)/Γ, in inﬁnite time. The distance traveled looks

like this, where for comparison, I have included the linear extrapolation of the initial velocity.

2 3

4 5

0.2

0.4

0.6

0.8

In Dave Morin’s book, he works out a slightly more interesting example in which there is also

a constant component of the force. This is relevant to objects falling in a gravitational ﬁeld and

also subject to friction. If the force looks like F (v) = F

− m Γ v, the velocity as a function of

time is

v(t) = v(t

) e

−Γ (t−t

)

m Γ

1 − e

−Γ (t−t

)

(16)

One interesting thing about this is that v(∞) =

m Γ

independent of v

. Whatever the initial condi-

tions, v approaches the same “terminal” velocity, as illustrated in the graph below:

2 3

4 5

0.5

1.5

2.5

If Γ is very large, this gives a kind of Aristotelian physics. When you push on something, it

moves with a velocity proportional to the force. If Γ is large enough, you might not notice that

it takes a little time (1/Γ) to settle down to this terminal velocity.

Another example: F (v) = −m β v

If an object moves rapidly through a gas, there is a frictional force proportional to v

. The force

arises because the object knocks the gas molecules out of the way, and the force is proportional

both to momentum change of the knocked molecules (which gives one factor of v) and to the

number of molecules that are knocked per unit time (another factor of v). Now let’s begin the same

analysis for such a force, of the form

F (v) = −m β v

(17)