Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)

Подождите немного. Документ загружается.

Now (3) becomes

= −

v(t)

v(t

)

β v

(18)

This looks nicer if we put the β on the other side

= −

v(t)

v(t

)

(19)

β (t − t

) =

v(t)

−

v(t

)

(20)

v(t)

v(t

)

+ β (t − t

) =

v(t

)

β v(t

) (t − t

)

v(t

)

1 + β v(t

) (t − t

)

v(t

)

(21)

v(t) =

v(t

)

1 + β v(t

) (t − t

)

(22)

I won’t work out the details here, but you can now integrate this again to get the position as a

function of time:

x(t) = x(t

) +

log

1 + β v(t

) (t − t

)

(23)

I did another example basically just to show how differently the initial condition (the value

of v(t

) in this case) comes into to the ﬁnal result in different cases [compare (22) and (23) with

(11) and (15)]. The trajectories always depend on two initial conditions, but what that dependence

looks like depends on the form of the force. You have to think and keep your wits about you — if

you try to remember formulas for all the different possible force laws, you will just get confused.

Instead concentrate on understanding the derivations! But nevertheless the matra — two initial

conditions per degree of freedom will be a useful check that you are doing sensible things.

Forces of the form F (x)

In this situation, we have to be a little less direct. We begin with F = ma in the form

= F (x) (24)

Multiplying both sides by v and using v = dx/dt we can write

m v

= F (x)

m v

(25)

We can now integrate both sides from t

to t to get

− v(t

)

x(t

)

F (x

) (26)

Next time we will see this again when discuss conservation of energy.

This determines v in terms of x. And then we can determine x(t) using

dt =

v(x)

(27)

which implies

= t − t

x(t

)

v(x

)

(28)

While this formally determines everything, this analysis is usually not very useful, because it is

only for very carefully chosen force laws that you can actually integrate and solve explicitly twice.

This can get complicated. If we are doing well on time, I will work out the example of a force of

the form

F (x) = b e

k x

(29)

using Mathematica. The results are in a Mathematica notebook on the website.

Meanwhile, we should note that this trick is related to conservation of energy, which we will

discuss next week.

Review of the harmonic oscillator

In general, if the force depends on both x and v (or x, v and t), things are much harder. But there

is one special system in which we can include both x and v dependence, and t dependence as well,

and still say interesting things rather simply. This is harmonic oscillator.

The harmonic oscillator is a very important mechanical system. We will start today at the

beginning but will go on to try to explain why it is important. The simplest example of a harmonic

oscillator is a mass attached to a spring, shown here sitting on a surface, which I will assume is

frictionless.

ªªªªªªªª

¤¡ ¤¡ ¤¡ ¤¡ ¤¡ ¤¡ ¤¡ ¤¡

-¾

(30)

There is an equilibrium position in which the spring is neither stretched nor compressed. In

equilibrium, the spring produces no force on the mass. If the mass moves so that the spring is not

in equilibrium, the spring exerts a force on the mass that tends to move it back to equilibrium. If

the mass is released from out of equilibrium, it accelerates towards the equilibrium position. When

it gets to the equilibrium position, the force goes to zero, but it is moving, so inertia keeps it going

to the other side of equilibrium. This is the classic recipe for oscillation.

But so far, this is just oscillation. What makes this a harmonic oscillator is the special force law

of the ideal “Hooke’s Law” spring, in which the force is proportional to minus the displacement

from equilibrium. If the block moves in the x direction, and we choose a coordinate system in

which x = 0 at equilibrium, then the force on the block looks like

F = −K x (31)

where K is called the spring constant. The larger the spring constant, the stiffer the spring.

Now Newton says

F = m a = m

x = m ¨x = −K x (32)

This is a force law that depends only on x, so we could ﬁnd the solution using the technique that

we just described for F (x) = −Kx. This works, but it is tedious. It is easier to just solve the

differential equation. You probably know that the general solution to the second order differential

equation (32) is

x(t) = a cos ωt + b sin ωt (33)

where

ω ≡

(34)

We can check this by differentiating (33):

˙x(t) = −aω sin ωt + bω cos ωt (35)

¨x(t) = −aω

cos ωt − bω

sin ωt = −ω

(a cos ωt + b sin ωt) = −ω

x(t) (36)

so that

m ¨x(t) = −m ω

x(t) = −m

x(t) = −K x(t) (37)

The constant ω is called the angular frequency. It is ﬁxed by the physics - the values of

the mass and the spring constant. But as we expected, there are an inﬁnite number of possible

trajectories, labeled by two constants, here a and b. Again as expected, we can determine a and b

by imposing initial conditions. The details of the way the constants enter are different here than

in our previous examples, but at least the number of initial conditions is right — two constants for

one degree of freedom. Setting t = 0 in (33) gives

x(0) = a cos 0 + b sin 0 = a (38)

Thus a is the position of the mass at t = 0. Setting t = 0 in (35) gives

v(0) = ˙x(0) = −aω sin 0 + bω cos 0 = bω (39)

Thus bω is the velocity of the mass at t = 0. Thus we can rewrite (33) as

x(t) = x(0) cos ωt +

v(0)

sin ωt (40)

As we will discuss in more detail later, we can easily adapt (40) to use the initial conditions at any

time t = t

as follows:

x(t) = x(t

) cos

ω(t − t

)

v(t

)

sin

ω(t − t

)

(41)

It is interesting to collect the various examples we have discussed in one table.

Force x(t)

⇒ x(t

) + v(t

) (t − t

) +

(t − t

)

−m Γ v ⇒ x(t

) +

v(t

)

1 − e

−

Γ (

−

)

−m β v

⇒ x(t

) +

log

1 + β v(t

) (t − t

)

−m ω

x ⇒ x(t

) cos

ω(t − t

)

v(t

)

sin

ω(t − t

)

(42)

What I think is interesting about this is that it shows very clearly that while each of these force

laws requires two initial conditions, which we can take to be the position and velocity at the time

, the way in which these two constants appear differs dramatically from one force law to another.

This is an important lesson. There are always two initial conditions per degree of freedom, the way

the initial conditions appear in the trajectory depends on the force law.

There is a very different way of writing the solution (33). Using (I hope familiar) trigonometric

identities, we can write

x(t) = a cos ωt + b sin ωt = c cos(ωt − φ) (43)

= c (cos ωt cos φ + sin ωt sin φ) (44)

= c cos φ cos ωt + c sin φ sin ωt (45)

a = c cos φ b = c sin φ (46)

c =

√

+ b

φ = arctan

(47)

The constant c is called the amplitude of the motion and φ is the phase of the oscillation. (44)-(47)

show that the two constants c and φ carry the same information as the two constants a and b. Both

pairs are determined by the initial conditions and either pair completely determines the trajectory.

The connection between these constants and the trajectory is illustrated in (48), a graph of the

trajectory x(t) versus t.

slope is b ω

2π

t →

↑

(48)

Because the sin and cos functions are periodic with period 2π,

x(t + 2π/ω) = c cos [ω(t + 2π/ω) − φ] = c cos(ωt − φ + 2π) = c cos(ωt − φ) = x(t) (49)

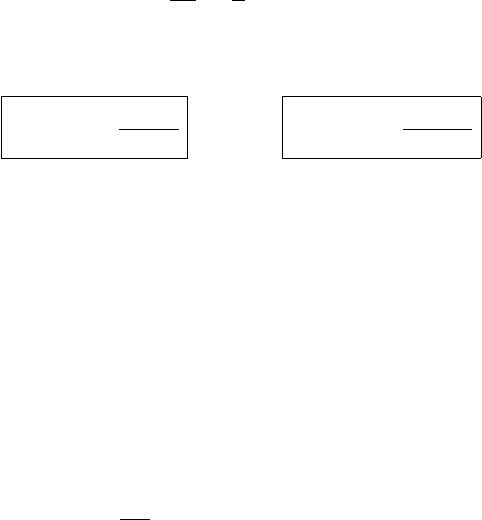
and thus the motion repeats after a time

τ = 2π/ω which is called “the period of the oscillation.” (50)

The frequency (as opposed to the angular frequency) is

ν =

2π

(51)

The product ωt — the argument of sin and cos is an angle.

Note that ν has units

cycles

sec

and ω has units

radians

sec

. (52)

These are really the same units in the sense of dimensional analysis because 2π is dimensionless,

but thinking about the units as stated in (52) will help you remember the factor of 2π which is just

the conversion factor between radians and cycles. It will make even more sense soon when we

make the connection between harmonic oscillation and uniform circular motion.

So what is it that is special about harmonic oscillation? — two general principles —

Linearity and Time Translation Invariance

Harmonic oscillation occurs almost everywhere. There are lots of physical systems whose motion

is described, at least approximately, by solutions to the same equation as the mass on a spring.

Why is that?

x + K x = 0 (53)

There are two key features.

1: Time translation invariance — there is no explicit dependence on time. There are dts — in

the derivatives with respect to time. But there are no ts. When the equation for motion has this

property, it follows that if x(t) is a solution then so is x(t + a). You can easily prove this using

the chain rule.

Time translation invariance is particularly useful for the harmonic oscillator because of the

other special property of its force law.

2: Linearity — because all the terms are proportional to one power of x or its derivatives, we can

make new solutions as linear combinations of old ones — if x

(t) and x

(t) are solutions then

so is A x

(t) + B x

(t). Again, this can be checked explicitly.

Time translation invariance is physically very reasonable. The laws of physics don’t change

with time. Or if they do, they do so very slowly (maybe on the scale of the age of the universe, 15

billion years or so), so that we can’t tell. There are lots of systems in which the coefﬁcients (things

like mass, spring constant, inductance, capacitance, etc) are determined directly by the laws of

physics and are therefore independent of time.

Linearity may seem more like an obscure mathematical concept — what does it have to do

with physics? Why should there be so many systems that are approximately linear? The word

“approximately” here is important. Probably, linearity is never exactly true for a classical system,

but it is often an excellent approximation.

So suppose that you are studying oscillations in some system, and all you know about it is that

it oscillates about a point of equilibrium. Let’s call the quantity that measures the displacement

from equilibrium x, to make it look like the mass on a spring. We expect that the time evolution

of the system can be described by the solutions to some second order differential equation (like

F = m a):

x = F(x) (54)

where F is the analog of the F/m in F = m a. Because I’ve assumed that we are in equilibrium

at x = 0, it must be that

F(0) = 0 (55)

Now, assuming that F(x) is smooth, we can use the most important formula in physics — and you

can probably guess what that is — the Taylor expansion

F(x) = F(0) + xF

(0) +

(0) + ··· = xF

(0) +

(0) + ··· (56)

Then unless F

(0) is exactly zero, the ﬁrst term will dominate for sufﬁciently small x. This is

why linearity is so important. Most functions in physics are smooth. Most of the time, there is no

particular reason for F

(0) to be zero, so it isn’t. Thus the equations of motion for most systems

are linear for sufﬁciently small x.

I should perhaps just note that the most important example of linearity has little to do with

classical mechanics — it is quantum mechanics itself. Just as classical sound waves or electromag-

netic waves can add together and sometimes interfere constructively and sometimes destructively,

so also the mysterious quantum matter waves that describe quantum states can be added. As far

as we know, the linearity of quantum mechanics is exact, not an approximation. At least, very

sensitive experiments have failed to ﬁnd any nonlinearities.

Next time, we will discuss the consequences of time translation invariance and linearity in

detail. We will see that when the physics of a system obeys these two general principles, the

trajectories can be written in a very simple form, as sums of exponentials. But sometimes, the

exponentials will be complex — that is they will involve i =

√

−1. Furthermore the generality

of argument will allow us to extend this result to systems with arbitrary numbers of degrees of

freedom, with rather dramatic results.

Back to F (v) = −m Γ v

For now, let us now return to the force law that we considered at the beginning of this lecture,

F (v) = −m Γ v. What is the physics of this force law? We saw that when friction arises because

stuff gets knocked out of the way, we get a v

dependence on velocity. But this v

dependence is

not linear. When v

is sufﬁciently small, we might expect that this effect will become negligible

compared to other effects that give a linear dependence on velocity. Indeed, in most liquids, we get

an approximately linear dependence of the frictional force on velocity for objects that are moving

slowing enough. Then the molecules of the liquid are not so much knocked as they are gently

pushed out of the way, so that the process is very smooth and reversible. This is a good excuse

to show you one of my very favorite demos, illustrating the smoothness that one gets in a in very

viscous medium, in which the linear regime is easy to reach.

lecture 3

Topics:

Where are we?

Consequences of Time Translation Invariance and Linearity

Uniform circular motion

Harmonic oscillation for more degrees of freedom

The double pendulum

The damped harmonic oscillator

Where are we?

Last time, we saw how initial conditions appeared in a number of different examples of force laws.

The last of these, the harmonic oscillator, is a particularly important system because it has two

general properties, time translation invariance and linearity, that appear in many many physical

systems.

Because linearity went by pretty quickly last time, let me brieﬂy review how it works. The

equation of motion, F = ma, for the harmonic oscillator is linear because there is a single x in

each term. It can be written as

+ K x = 0 (1)

We can think of this as a single “operator” acting on x.

+ K

x = 0 (2)

In this form, it may be more clear why you the solutions form a linear space. If you have two

solutions, x

(t) and x

(t), you can form an arbitrary linear combinations and still get solutions,

because the same operator acts on both, and multiplying by a constant doesn’t affect the validity

of the solution,

+ K

= 0

+ K

= 0

⇒

+ K

(a x

+ b x

) = 0

(3)

This fact has remarkable consequences, as we will see shortly.

Consequences of Time Translation Invariance and Linearity

Time translation invariance is an example of a symmetry. The physics of the harmonic oscillator

looks the same if all clocks are reset by the same amount. When a symmetry is combined with

the property of linearity, the result is an extremely powerful tool for studying the solutions of the

system’s equation of motion. The reason is that because of linearity, the solutions of the equation

of motion form what mathematicians call a linear space. You can add them together and multiply

them by constants and you still have solutions. Because of this, we can use the tools of linear

algebra to understand them. In particular, we can choose a convenient set of basis solutions that

behave as simply as possible under time translations. For the symmetry of time translation, it is a

mathematical fact that the basis solutions are just exponentials. We can always ﬁnd solutions of

the form

z(t) = z(0) e

(4)

What is special about this form (and I am not going to discuss this in detail - I hope that you will

see this beautiful argument in more detail in Physics 15c) is that when you change the setting of

your clock by taking t → t + a, the exponential (4) is the only function that just changes by a

multiplicative constant,

z(t + a) = z(0) e

H(t+a)

= z(0) e

= e

z(t) (5)

You can always use the linearity of the space of solutions to ﬁnd particularly convenient solutions

that behave in this simple way under time translations - and then the result has to be an exponential.

Once you realize that the solutions are just exponentials, you can ﬁnd the possible values of H

in a very simple way. If you do take (4) and put it into the equation of motion, time derivatives

acting on e

just bring down factors of H. This converts the differential equation into an algebraic

equation.

→ H (6)

Then once we have the basis soltutions, we can form linear combinations to satisfy the initial

conditions, in the same way that we can write a general vector in three dimensional space as a sum

of coordinates times basis vectors

~r = x ˆx + y ˆy + z ˆz

This simple dependence of ~r on the coordinates x, y and z is the power of linearity at work. We will

see that it works in a similarly simple way for the initial conditions in a linear and time translation

invariant mechanical system.

Let’s do this for the linear frictional force we talked about last time, of the form

−m Γ v (7)

with

Γ ≥ 0 (8)

We know how to solve this directly by integrating, as we did last time, but you will notice, I hope

that this force law is also time translation invariant and linear. There is just a single factor of x in

v =

(9)

and t enters only through derivatives. Therefore, we expect that the solution is a sum of exponen-

tials in time times coefﬁcients that depend on the initial conditions. The equation of motion has

the form

m ¨x = −m Γ ˙x (10)

This is essentially equivalent to the statement that a linear differential equation with constant coefﬁcients always

has an exponential solution — see Morin’s text.

This allows us to solve the problem in a different way, by assuming that the solution is a linear

combination of exponentials. If we put in a trial solution of the form

x(t) = e

H t

(11)

each dot becomes a factor of H and we get

m H

H t

= −m Γ H e

H t

(12)

= −Γ H ⇒ H = −Γ or H = 0 (13)

so there are two simple solutions,

x(t) = e

= 1 and x(t) = e

−Γ t

(14)

The general solution, because of linearity, is then a combination of these two solution with coefﬁ-

cients that depend on the initial conditions:

x(t) = A + B e

−Γ t

(15)

Comparing with the solution that we got by direct integration,

x(t) = x(t

) +

v(t

)

1 − e

−Γ (t−t

)

(16)

we see that it is equivalent to (15) with

A = x(t

) +

v(t

)

(17)

and

B = −

v(t

)

Γ t

(18)

I hope you agree that this calculation was quite a bit easier and quicker than integrating. Using

these general principles of time translation invariance and linearity is not only cool, it saves you

work. As you will see in more complicated examples in a few minutes, it often saves you a LOT

of work!

Before going on to the harmonic oscillator, let’s describe this process in the form of two simple

steps for dealing with systems with time translation invariance and linearity:

1. Put a trial solution of the form e

into your equation of motion. The derivatives become

powers of H and you can ﬁnd the values of H = h

that work by solving an algebraic

equation. This gives you your basis solutions e

2. Write a general solution by making a general linear combination of your basis solutions —

x(t) =

(19)

and ﬁnd the constants A

by imposing initial conditions, as usual.

The only time this procedure doesn’t work is when the algebraic equation you get has degenerate roots. We will

see what to do in this special case later.

Now let’s apply these two steps for the mass on the spring. Step 1 is straightforward.

m ¨z(t) = −K z(t) (20)

z(t) → e

(21)

= −K e

(22)

m H

= −K e

(23)

m H

+ K

= 0 (24)

m H

+ K = 0 (25)

H = ±iω for i =

√

−1 and ω =

(26)

So our two basis solutions are

iωt

and e

−iωt

(27)

The calculation in step 1 was very simple. The only curious thing here is that we are led to

complex numbers. While time translation invariance tells us that there are solutions of the form

, it doesn’t tell us that H is real, and for oscillations, it isn’t.

Now in step 2, we form the general solution by forming a general linear combination of our

basis solutions. Thus the most general solution for the harmonic oscillator looks like this:

x(t) = c e

iωt

+ d e

−iωt

(28)

Now this is a little peculiar. Unlike the situation with the frictional force, in (16), this doesn’t look

the same as the cosine and sine that we got by solving the differential equation. But in fact, it is the

same. The connection with sines and cosines is Euler’s formula, one of the more amusing relations

in mathematics:

iθ

= cos θ + i sin θ (29)

There are many ways of seeing this. Let’s just use the most important formula in physics again —

Taylor’s expansion

iθ

= 1 + (iθ) +

(iθ)

+ ··· (30)

1 −

(θ)

+ ···

+ i

θ −

+ ···

(31)

Because of Euler’s formula, you see that the general solution in terms of cosine and sine is

completely equivalent to the general solution in terms of complex exponentials.

x(t) = a cos ωt + b sin ωt

is equivalent to

x(t) = c e

iωt

+ d e

−iωt

= c (cos ωt + i sin ωt) + d (cos ωt − i sin ωt)

a = c + d b = i(c − d)

(32)