Georgi, Howard. Physics 16 - Mechanics and Special Relativity (англ.)
Подождите немного. Документ загружается.


superno
va.
↑
t
x →
0
.
..................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
light is
emitted
here
this is our
guess from
the redshift
assuming
constant
expansion
and current
value of H
.....................................................................
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
the supernova is
farther away
and therefore
dimmer than
we expect
from the
redshift
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
..
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Two groups have independently seen this effect. One is a local group involving my neigh-
boring Master, Bob Kirshner, in http://arxiv.org/abs/astro-ph/9805201. The other is a group from
Berkeley: http://arXiv.org/abs/astro-ph/9812133.
If all this is right, it implies that about 70% of the energy density of the universe, which it seems
is roughly equal to the critical density required for flatness, comes from the energy of the vacuum.
This is a bizarre, crazy result that I have a lot of trouble believing, for reasons that I will come
back to. I would not be surprised if the result changed as more data is accumulated. However, it
has been around for several years now as the number of supernovas on which the estimate is based
has grown from a few to hundreds. There is also growing indirect support for this view from the
consistency of the measured anisotropy of the CMBR with a model in which 30% of the energy
density of the universe is in the form of cold dark matter and the rest is energy density.
It is still hard to believe, but who knows. Here are some links to more recent information.
The most distant supernova - so far away that the the universe was still slowing down
The technical paper on the most distant supernova
The laws of physics and the Taylor expansion
Now finally, I want to return to the question that we discussed at the very beginning of the course.
Why is
~
F = d~p/dt? Why is Newton’s law a formula for acceleration? Of course, we know that
12

Ne
wton’s law is not right. It ignores special relativity and quantum mechanics, for example. But
in fact, our current theories of relativistic quantum mechanics are based on Lagrangians that are
really rather straightforward generalizations of those that we use to derive Newton’s law. The
Lagrangians that we use to describe the world still depend just on coordinates and their first time
derivatives. The equations of motion are thus still equations for “acceleration.” So in a certain
sense, Newton has survived the revolutions of special relativity and quantum mechanics, and the
question still remains an interesting one. I certainly don’t know the answer to this question. But I
think that it is related to a much deeper question, which may be the central mystery of the way the
universe works.
This mystery takes a bit of explaining. We have already talked about particle physics units, in
which ¯h and c are set equal to 1 because they are built into the way the universe works. If we adopt
these sensible units, then all dimensional quantities can be related. For example, we can express
everything in terms of mass. The properties of our world are primarily determined by the masses
of the electron and the proton, and a few numbers, like the fine structure constant, α =
e
2
¯hc
≈
1
137
.
Almost
all of the physics of the everyday world involves combinations of these basic parameters.
But one thing that is different is gravity. Gravity, you remember, is described by the gravitational
constant G, which in particle physics units is proportional to 1/m
2
Planck
where the Planck mass is
enormous, about 10
19
times the mass of the proton. G, is very very very tiny compared to any
quantity with the same units that we might construct out of the parameter that describe the rest of
our everyday world.
Why should we care about gravity? Well, aside from the fact that it keeps us from flying off
into space, there is a theoretical problem associated with gravity. It seems to be impossible to put
special relativity, quantum mechanics, and gravity together consistently, without changing the rules
in some way. This suggests that the Planck mass is the basic scale at which really interesting new
physics, some change of the rules beyond special relativity and quantum mechanics, is happening.
This is a very dicey argument, for various reasons,
3
but let’s assume that it is right. Then special
relativity and quantum mechanics, and with them Newton’s law, are just approximations that are
true for masses much smaller than the Planck mass.
Now the important point is this. Every dot in the Lagrangian, every derivative with respect to
time, in particle physics units, has units of mass (because a derivative is one over a distance). But
if the fundamental scale is the Planck mass, each dot should come generically with a power of
1/m
Planck
. Because m
Planck
is so huge, the terms with more than the minimum number of dots can
be ignored. They are there, but their effects are very small, and we don’t see them.
If this is right, then
~
F = d~p/dt is just an approximation, but it is a very good one because
gravity is so weak. The central mystery, then, is why is gravity so weak? Why is the Planck mass
so very much larger than all the other masses that we care about in physics? This seems crazy.
Where does the tiny dimensionless ratio of the proton mass to the Planck mass, about 10
−19
come
3
F
or example, maybe someone will discover a clever way of doing it. People are trying. Maybe the string theorists
have already done it, but they have really changed the rules, so this would just be an example of what I am saying.
Or maybe the rules change again well before the Planck scale, and gravity emerges in some complicated way from
physics at smaller masses. There are also some interesting ideas of this sort on the market today.
13

from?
Who know? Maybe one of you will figure it out, or maybe you will show that it is not the
right question.
In closing, let me finally come back once more to the cosmological constant. If the recent
reports of a nonzero energy density of the vacuum are correct, this is ever crazier that the mystery
of the proton mass. To see this, lets convert this cosmological constant to particle physics units.
The statement is that the cosmological constant is about 70% of the critical density. The critical
density is given by
µ
˙a
a
¶
2
=
1
T
2
=
8π
Gρ
c
3
(8)
where T is
the Hubble time, very roughly 10
10
yr. So
ρ
c
≈
3
8π
GT
2
(9)
The 1/G is just m
2
Planck
. One year is about π × 10
7
seconds. The way I remember how to do these
unit conversions is to convert things first to a funny unit of mass - billion electon volts - GeV -
which is about the mass of the proton. In these units, one second is about 10
24
GeV
−1
. But the
Planck mass is even larger, about 10
19
GeV, so 1 second is about 10
43
m
−1
Planck
. Thus a year is about
10
50
m
−1
Planck
(we can certainly drop the factor of π) and the Hubble time is about 10
60
m
−1
Planck
.
Thus
ρ
c
≈ 10
−120
m
4
Planck
(10)
This is an even smaller dimensional scale than the proton mass. That is why it seems so crazy.
Where does this tiny number come from? This situation is much worse even then the ratio of 10
19
between the Planck mass and proton mass. If we had to guess from first principles the energy
density of the universe, we would guess that the scale is set by the Planck mass, so we would
guess m
4
Planck
. We missed it by about a factor of 10
120
. This wasn’t a very good guess! I think it
is probably the worst guess in the history of mathematical science. What went wrong? Nobody
knows. But it is suspcious that no only is it very small, but it is not so different from the critical
density of the universe today.
There are two kinds of ideas that people have discussed to try to explain away this puzzle. Many
theorists believe that it has something to do with an odd kind of symmetry - called supersymmetry
- which would imply an equivalence between matter particles and force particles. If this symmetry
were exact, the cosmological constant would be zero. Unfortunately, we don’t see this symmetry
- it is certainly broken in our world - and nobody have found a plausible explanation of how the
symmetry could be broken, and still force the cosmological constant to be small.
The other set of ideas is even crazier and goes by the term “Anthropic argument.” This is an
updated version of an old idea that the laws of physics are what they are because if they were
different, we wouldn’t be here to study them. The modern version of this goes something like this.
Suppose that vacuum is a much more complicated thing than I have described to you, and actually
the structure of the vacuum in which we live depends on many many parameters, and the energy of
the vacuum is a complicated “landscape” with lots of peaks and basins. A two dimensional verison
14
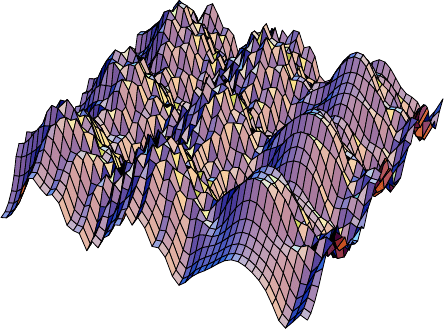
really
does look like a landscape —
b
ut of course the multidimensional version is much more complicated and hard to visualize. If
the vacuum looks like this, and quantum mechanics is causing fluctuations in this complicated
structure, then most regions in the huge chaotic universe are somewhere up on a hill, inflating away
like mad because of negative gravity. but in some regions the universe settles down into one of the
basins, producing matter and radiation which dominates the energy density. Then this region stops
inflating, at least for a while, until the ordinary Hubble expansion of this region of the universe
dilutes the matter and radiation and the cosmological constant dominates the energy density. Then
the expansion accelerates at a rate determined by the value of the energy density at the bottom of the
basin. This happens a huge number of times in different regions of the universe, in a huge number
of different basins, at random. Each basin will have a different of the cosmological constant. This
kind of universe is a kind of huge experimental laboratory with different experiments going on each
of the regions where the universe settles down. One constraint that many people think is relevant
has to do with the formation of galaxies. If the cosmological constant is too big in a basin, then
the space continues to grow so fast that matter doesn’t have a chance to fall into separate galaxies.
Then stars don’t form, planets don’t develop, and nobody gets to teach Physics 16. If you believe
that this is necessary, it goes a long way towards explaining why the cosmological constant is so
small.
I am not sure that this is science. But one could imagine getting enough information about
structure of this landscape to make predictions rather than just qualitatively explaining what we
see. That would be interesting.
At any rate, it seems clear that we need to understand the vacuum much better. If we are really
lucky, we will get some hints to what is going on by seeing some surprising property of the vacuum
15
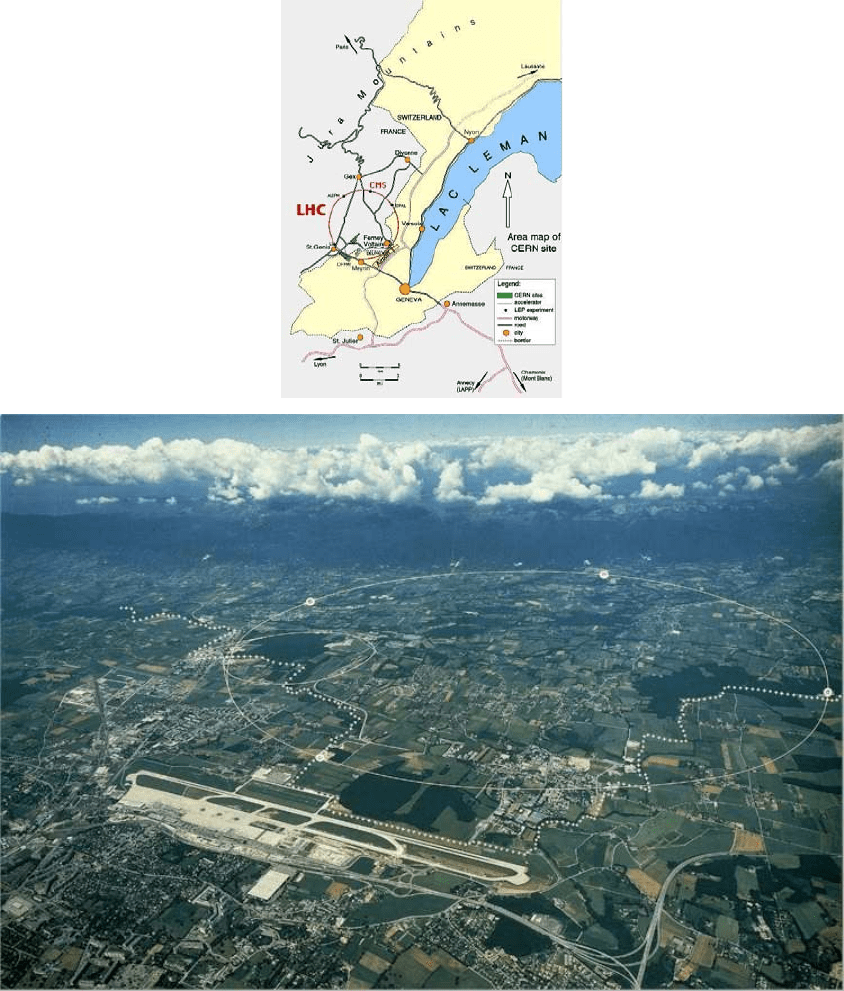
at
the LHC.
Abo
ve are a map and an arial photo of the CERN site, near the Geneva airport, where the LHC
is being constructed. This is a monster project involving many thousand scientists and engineers.
16

Belo
w is a photo in the tunnel - most of the 10 miles of it looks like this.
It
is pure speculation at this point to think that the LHC may teach us something about the dark
energy. But it could happen. Certainly, the LHC will be our first opportunity to directly probe the
mysterious physics of the vacuum, of which the dark energy seems to be another manifestation.
That should make the next ten years an incredibly exciting time for fundamental physics.
17
