George W. Stimson introduction to Airborne Radar (Se)

Подождите немного. Документ загружается.

CHAPTER 31 Principles of Synthetic Array Aperture Radar

417

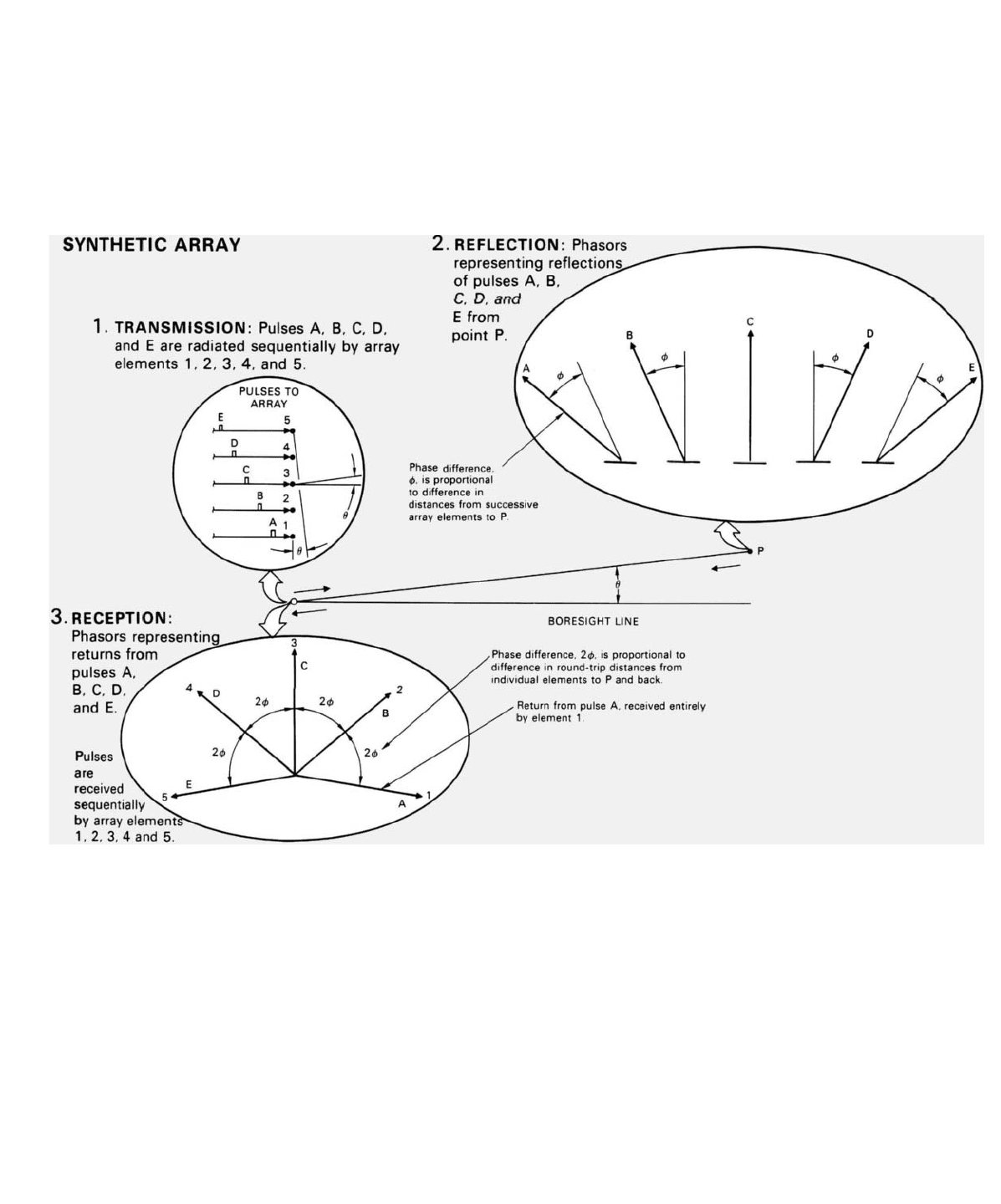
Synthetic Array. In the case of a synthetic array, transmission

bmthe individual array elements is sequential. The first pulse is

transmitted and received entirely by the first element; the second

pulse, entirely by the second element; and so on. Consequently,

the returns received by successive elements differ in phase by

amounts proportional to the differences in the

round-trip

distance

from each element to P and back to the element again.

Thus, for any one angle off the boresight line, the progressive

shift in the phases of the returns received by successive array

elements is twice as great for a synthetic array as for a real array

(The doubling of phase shift gives the beam of the synthetic

array its sin 2x/2x shape.)

Significance. Because of the doubling of phase shifts, the null-to-

null beamwidth of a synthetic array is only half the null-to-null

beamwidth of a real array of the same length. And the 3-dB

beamwidth is roughly 70 percent of the two-way 3-dB beamwidth

of the real array. (At the ⫺3 dB points, sin (2x/ 2x) ≅ 0.7 (sin x/x)

The doubling of the phase shifts must, of course, also be kept

in mind when calculating such factors as the phase corrections

necessary to focus an array and the angles at which grating lobes

(see Chapter 32) will occur.

PART VII High Resolution Ground Mapping and Imaging

418

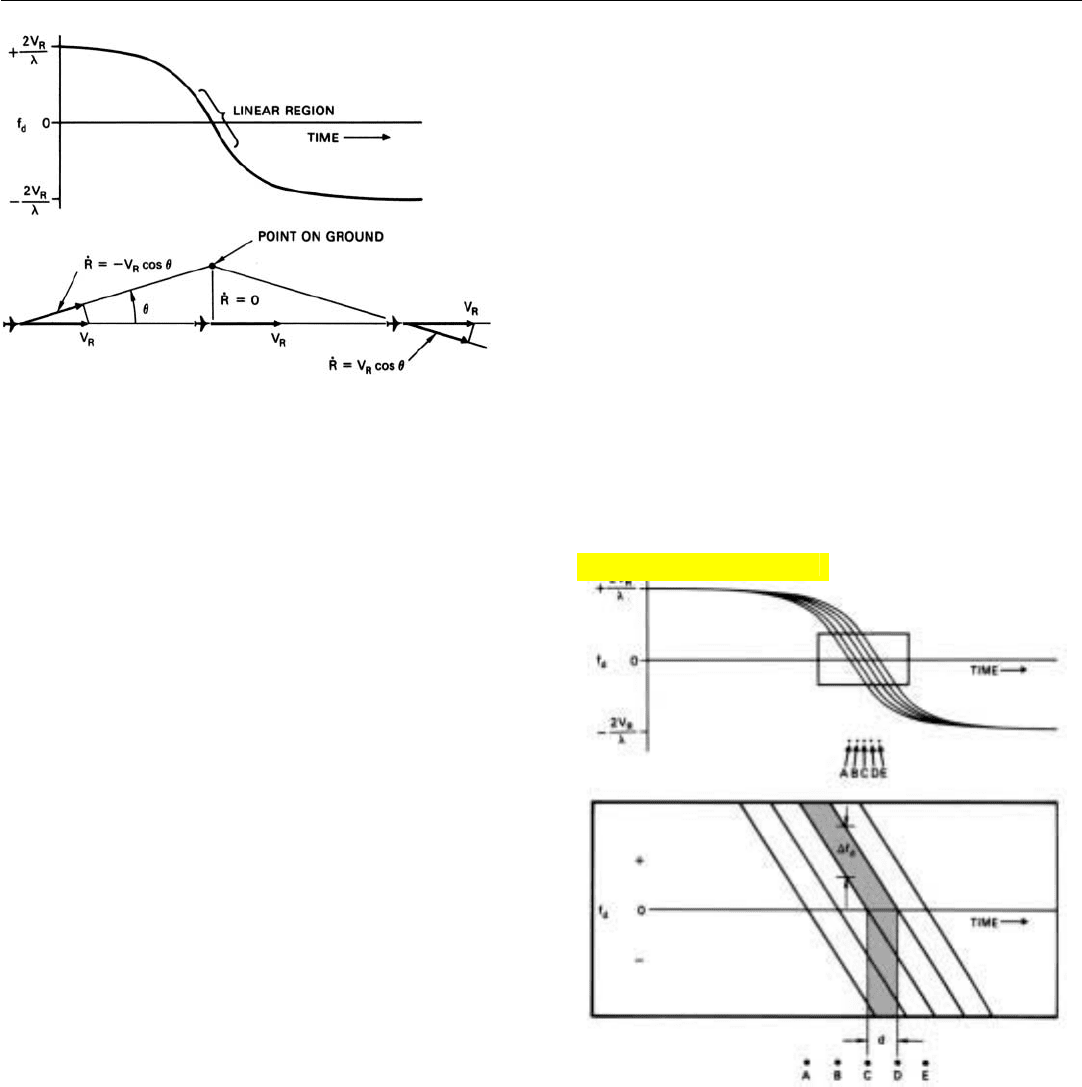
Doppler Frequency Versus Azimuth Angle. Figure 19

shows the doppler history of the return from a point of

ground offset from the radar’s flight path. When the point is

a great distance ahead, its doppler frequency corresponds

very nearly to the full speed of the radar and is positive.

When the point is a great distance behind, its doppler fre-

quency similarly corresponds to the full speed of the radar,

but is negative.

As the radar goes by the point, its doppler frequency

decreases at virtually a constant rate, passing through zero

when the point is at an angle of 90˚ to the radar’s velocity. If

the radar antenna has a reasonably narrow beam and is

looking out to the side at a reasonably large azimuth angle,

the point will be in the antenna beam only during this lin-

early decreasing portion of the point’s doppler history.

A plot of this portion of the doppler histories of several

evenly spaced points at the same offset range is shown in

Fig. 20.

19. As a radar passes a point on the ground, its doppler frequen-

cy decreases at a nearly linear rate, passing through zero

when the point is at an angle of 90

˚ to the radar‘s velocity.

20. Doppler histories of evenly spaced points on the ground. The

instantaneous frequency difference, ∆f

, is proportional to the

azimuthal distance between points, d.

As you can see, the histories are identical—the frequency

decreases at the same constant rate—except for being stag-

gered slightly in time. Because of this stagger, at any one

instant, the return from every point has a slightly different

frequency. The difference between the frequencies for adja-

cent points corresponds to the azimuth separation of the

points. We can isolate the return received from each point,

therefore, by virtue of this difference in doppler frequency.

Click for high-quality image

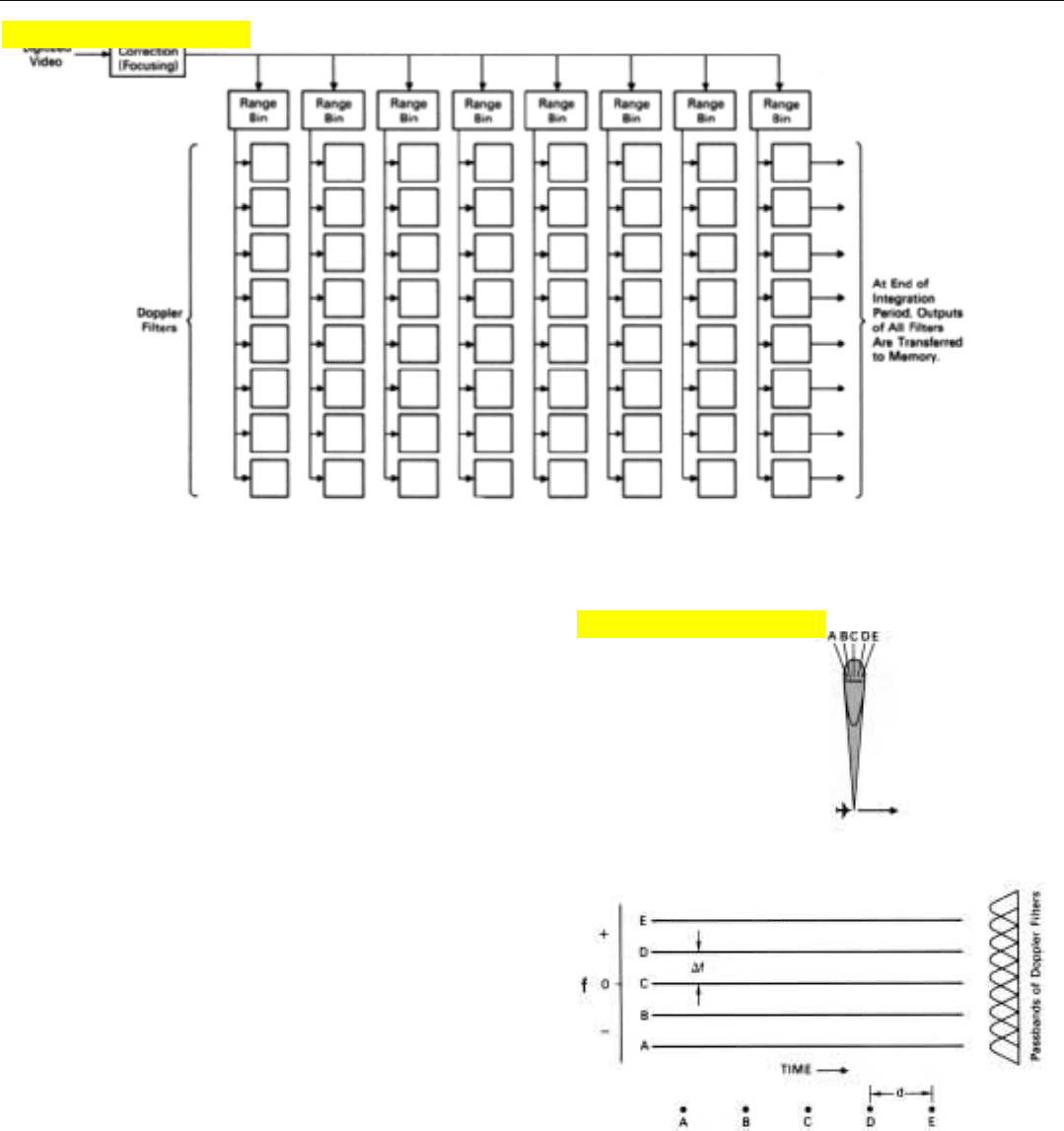
Implementation. The block diagram of Fig. 21 (above)

indicates in general how doppler processing is done.

At the outset, a phase correction is made to the returns

received from each pulse to remove the linear slope of the

doppler histories (i.e., to focus the array). This process,

called focusing, converts the return from each point on the

ground to a constant doppler frequency (Fig. 22). That fre-

quency corresponds to the azimuth angle of the point, as

seen from the center of the segment of the flight path over

which the return was received.

Every time the aircraft traverses a distance equal to the

length of the array that is to be synthesized, the phase-cor-

rected returns which accumulate in each range bin are

applied to a separate bank of doppler filters. Thus, for every

array length, as many banks of filters are formed as there

are range bins. The integration time for the filters is the

length of time the aircraft takes to fly the array length. The

number of filters included in each bank correspondingly

depends upon the length of the array. The greater it is (hence

the longer the filter integration time), the narrower the filter

passbands and the greater the number of filters required to

span a given band of doppler frequencies. The narrower the

filters, of course, the finer the azimuth resolution.

Since the frequencies to be filtered are relatively constant

over the integration time and (for uniformly spaced points

on the ground) are evenly spaced, the fast Fourier trans-

form (FFT) can be used to form the filters, greatly reducing

the amount of computation. Herein lies the advantage of

doppler processing.

CHAPTER 31 Principles of Synthetic Array Aperture Radar

419

21. How doppler processing is done. After focusing corrections have been made, returns are sorted by range. When returns from a complete

array have been received, a separate bank of filters is formed for each range bin.

22. A phase correction converts the return from each point on the

ground to a constant frequency, enabling the doppler filters to

be formed with the FFT.

Click for high-quality image

PART VII High Resolution Ground Mapping and Imaging

420

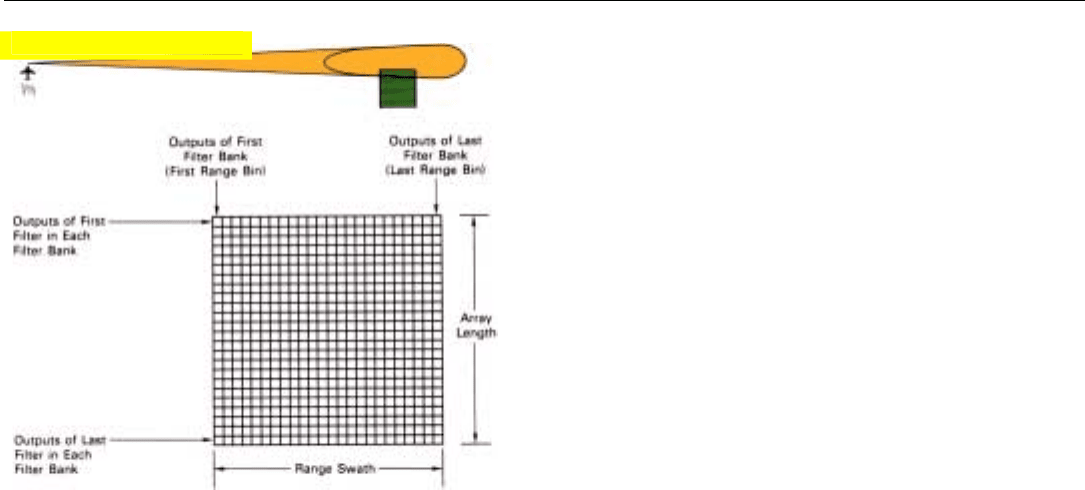
As required for the FFT, the filters are formed at the end

of the integration period, i.e., after the radar has traversed

an entire array length. The outputs of each bank of filters

represent the returns from a single column of resolution

cells at the same range—the range of the range bin for

which the bank was formed (Fig. 23). The outputs of all of

the filter banks, therefore, can be transferred as a block, in

parallel, directly to the appropriate positions in the display

memory. The radar, meanwhile, has traversed another array

length thereby accumulating the data needed to form the

next set of filter banks, and the process is repeated.

Incidentally, as illustrated in the panel on the facing page,

the focusing and azimuth compression process just

described is strikingly similar to the stretch-radar deramping

and range compression process for decoding chirp pulses.

Reduction in Arithmetic Operations Achieved. Having

gained (hopefully) a clear picture of the doppler-filtering

method of azimuth compression, let’s see what kind of sav-

ing in arithmetic operations it actually provides. To simplify

the comparison, we’ll assume that no presumming is done

by either processor.

In the doppler processor, phase rotation takes place at

two points: (1) when the return is focused, and (2) when

the doppler filtering is done. For focusing, only one phase

rotation per pulse is required for each range bin. As was

explained in Chap. 20, in a large filter bank the number of

phase rotations required to form a filter bank with the FFT

is 0.5N log

N, where N is the number of pulses integrated.

The total number of phase rotations per range bin for paral-

lel processing, then, is N + 0.5N log

N. For line-by-line

processing, as we just saw, the number of phase rotations

per pulse per range gate is N

Processing Phase Rotations

Line-by-line N

Parallel (doppler) N(1 + 0.5 log

To get a feel for the relative sizes of the numbers

involved, let’s take as an example a synthetic array having

1024 elements. With line-by-line processing a total of 1024

x 1024 = 1,048,576 phase rotations would be required.

With parallel processing, only 1024 + 512 log

1024 =

6,144 would be required. The number of additions and

subtractions would similarly be reduced. Thus, by employ-

ing parallel processing the computing load would be

reduced by a factor of roughly 170!

Correspondence to Conventional Array Concepts.

Superficially, doppler processing may seem like a funda-

23. The outputs of each filter bank represent the return from a sin-

gle column of range/azimuth resolution cells.

Click for high-quality image

CHAPTER 31 Principles of Synthetic Array Aperture Radar

421

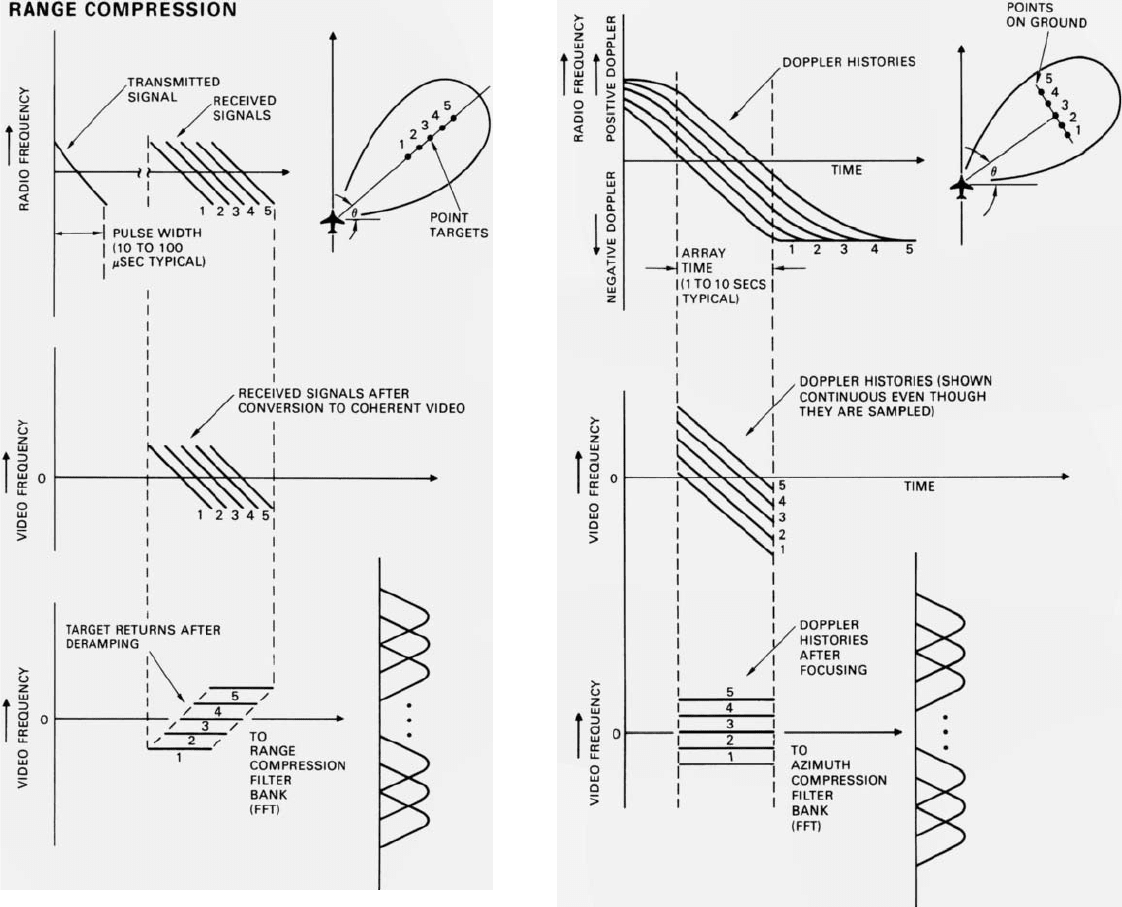
SIMILARITY OF AZIMUTH COMPRESSION TO

RANGE COMPRESSION WITH STRETCH RADAR

The focusing and azimuth compression performed in the

doppler processing of SAR signals are strikingly similar to the

deramping and range compression performed in the stretch-radar

decoding of chirp pulses(when that method of pulse compression

is used). The chief difference lies in the rate at which the

compression is performed. Whereas azimuth compression is

typically carried out over a period on the order of 1 to 10

seconds

range compression is typically carried out over a period on the

order of 10 to 100

microseconds

. In both cases, deramping

(focusing) may be performed either digitally, as described here,

or by analog means as described in Chapter 13.

PART VII High Resolution Ground Mapping and Imaging

422

mental departure from conventional array concepts. But it

is not. As we learned in Chap. 15, a doppler frequency is

nothing more nor less than a progressive phase shift. To say

that a signal has a doppler frequency of one hertz is but to

say that its phase is changing at a rate of 360˚ per second. If

the PRF is 1000 hertz, the pulse-to-pulse phase shift is 360˚

÷ 1000 = 0.36˚. Viewed in this light, the doppler histories

we have been considering are really phase histories.

Virtually every aspect of the doppler processor’s operation,

therefore, directly parallels that of the line-by-line processor

described earlier.

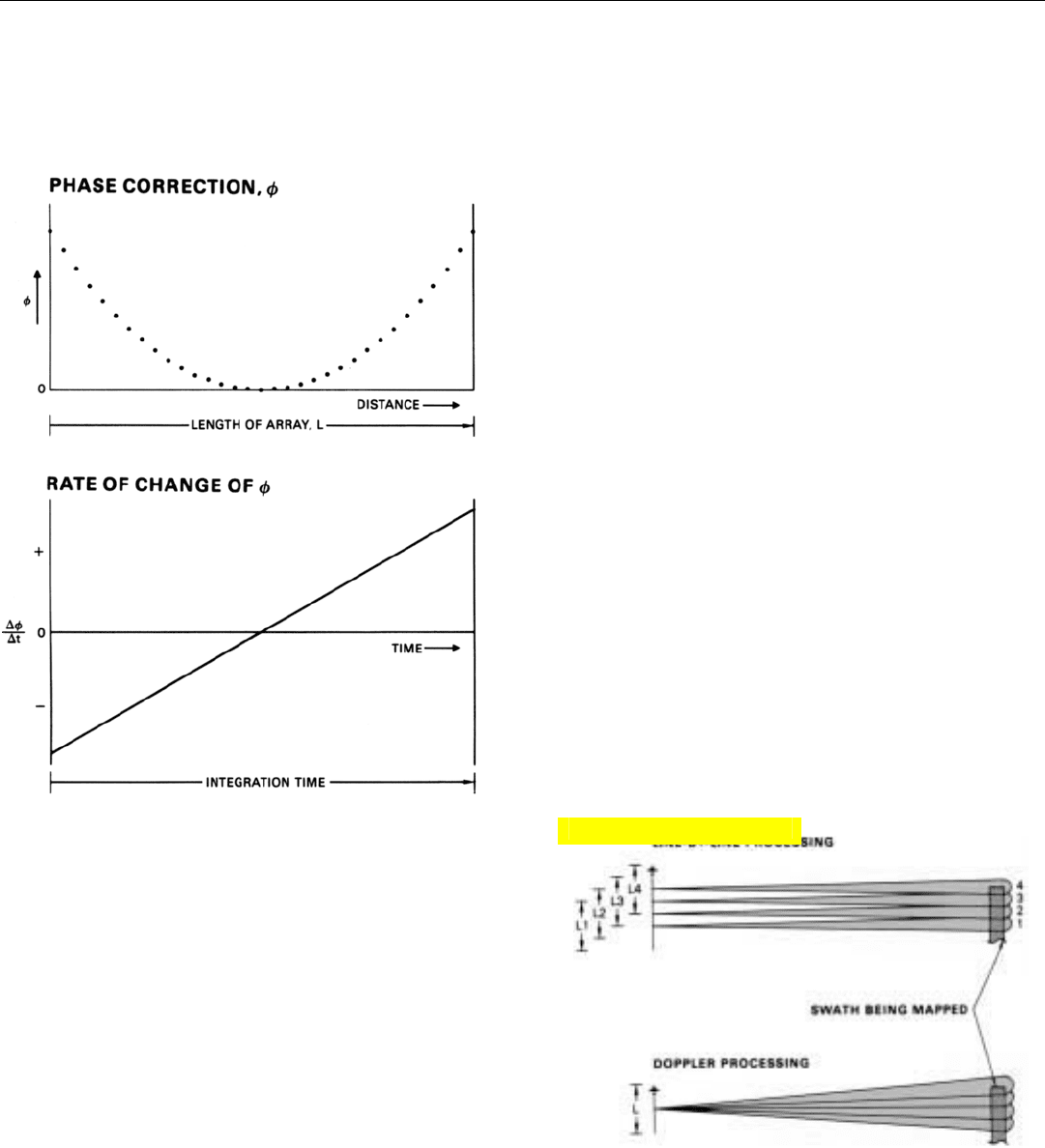
The phase corrections used to remove the slope of the

doppler history curves are exactly the same as the correc-

tions used to focus the array in the line-by-line processor.

This is illustrated by the graphs of Fig. 24. The “U” shaped

curve is a plot of the focusing corrections applied to the

returns received by successive array elements in line-by-

line processing. The straight diagonal line is a plot of the

rate of change of these corrections. Its slope, you will

notice, is identical to the slope of the doppler history of a

point on the ground but is rising, rather than falling. The

same focusing correction that is used by the line-by-line

processor, therefore, converts the linearly decreasing fre-

quency of the return from each point on the ground to a

constant frequency.

While not identical, the beams synthesized by the two

processors are virtually the same. The only difference is in

their points of origin (Fig. 25).

24. Focusing corrections, ø, made to return from successive blocks

of pulses. Rate of change of ø has same slope as doppler his-

tory of point on ground, but is rising rather than falling.

25. Synthetic array beams formed with line-by-line processing and

doppler processing differ only in their points of origin.

With the line-by-line processor, every time the radar

advances one azimuth resolution distance, d

, a new beam

is synthesized. Whereas, with the doppler processor, every

time the radar advances one array length, each doppler fil-

ter bank synthesizes a new beam.

Click for high-quality image

CHAPTER 31 Principles of Synthetic Array Aperture Radar

423

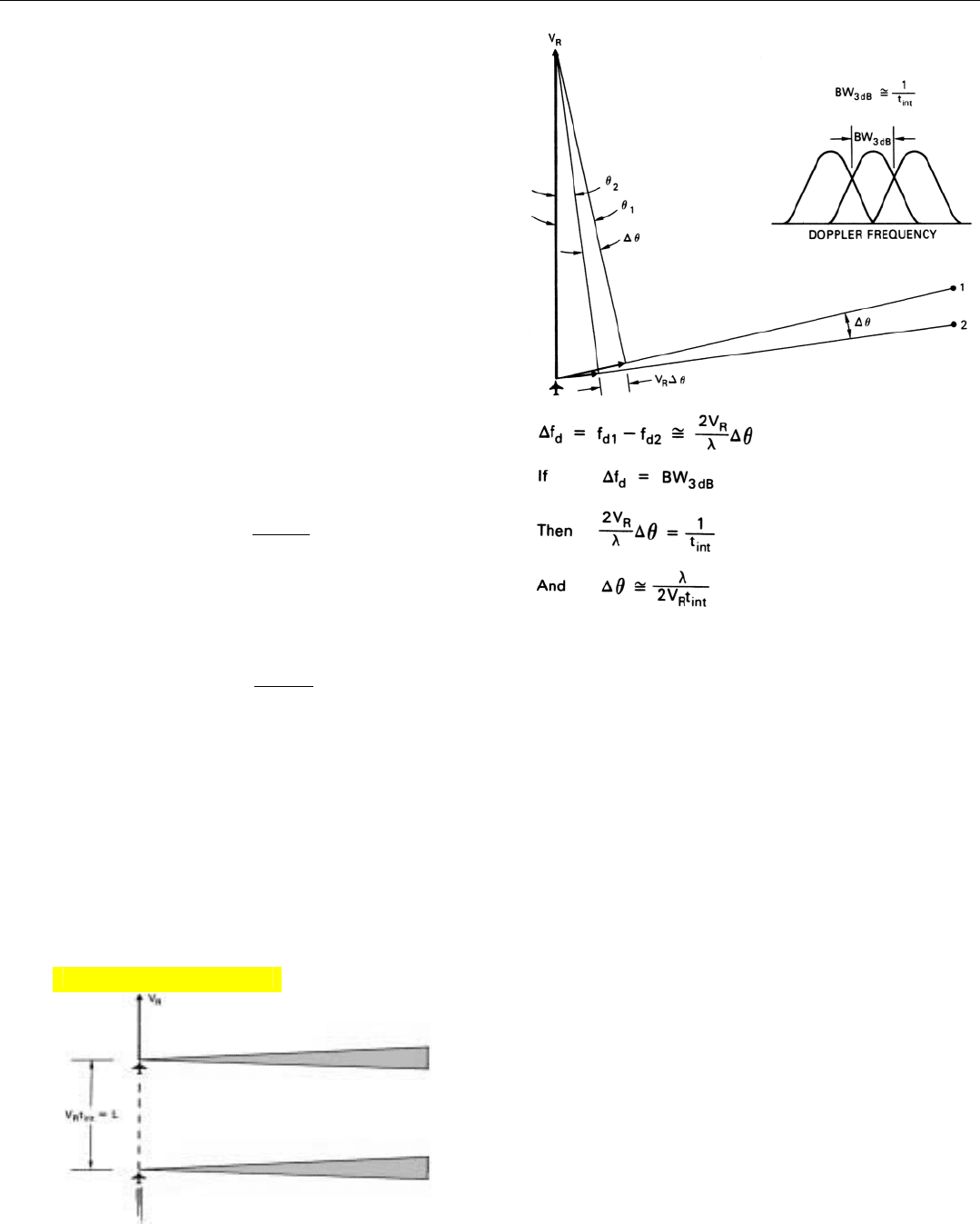
26. The 3-dB bandwidth of a doppler filter is one divided by the

integration time. The difference in doppler frequency, ∆f

, of the

returns from two points on the ground is proportional to their

angular separation, ∆

. Equating BW

3 dB

to ∆f

yields an

expression for the angular resolution.

27. The length of the array synthesized with doppler processing is the

distance flown during the integration time of the doppler filters.

The beams formed by the line-by-line processor all have

the same azimuth angle (90˚ in the example we have been

considering). But because of the radar’s advance, at the

range being mapped they overlap only at their half power

points.

The beams formed by the doppler filters, on the other

hand, all originate at the same point (center of the array).

But they fan out at azimuth angles such that they overlap

at their half power points.

And how do the azimuth resolutions provided by the

two processors compare?

The 3-dB bandwidth of the doppler filters is roughly

equal to one divided by the integration time (BW

3dB

≅

1/t

int

). As shown in Fig. 26, the difference between the

doppler frequencies of two closely spaced points on the

ground at azimuth angles near 90˚ is twice the radar veloci-

ty times the azimuth separation of the points, divided by

the wavelength.

∆f

∆

Equating ∆f

to BW

3 dB

and substituting 1/t

int

for it, we

obtain the following expression for the width of the beam

synthesized by the doppler processor.

∆

int

where

∆

= beamwidth

= radar velocity

int

= integration time

The product of the radar’s velocity and integration time,

int

, is the distance flown during the integration time. As

illustrated in Fig. 27, that is the length of the array, L.

Click for high-quality image

PART VII High Resolution Ground Mapping and Imaging

424

Substituting L for V

int

and multiplying by the range, R,

we find the azimuth resolution distance to be:

This is exactly the same as the azimuth resolution dis-

tance for the line-by-line processor: one half the resolution

distance for a real array of the same length.

So, whether you think of a synthetic array radar in terms

of doppler processing or of conventional array concepts is

largely a question of which view makes the particular aspect

of the array you are concerned with easier to visualize.

Summary

Fine azimuth resolution may be obtained by pointing a

small radar antenna out to one side, storing the returns

received over a period of time, and integrating them so as

to synthesize the equivalent of a long array antenna—SAR.

The points at which successive pulses are transmitted can

be thought of as the elements of this array.

Phase errors due to the greater range of a point on the

ground from the ends of the array than from the center

limit its useful length. The limitation may be removed

through phase correction, a process called “focusing.”

With focusing, azimuth resolution can be made virtually

independent of range by increasing the array length in pro-

portion to the range of the region being mapped.

Since that region must lie within the beam of the real

antenna throughout the entire time the array is being

formed, the length of an array having a fixed look angle is

limited to the width of the beam of the real antenna at the

range being mapped. (This limitation is removed in the

spotlight mode.) The smaller the real antenna, the wider its

beam will be, hence the longer the synthetic array can be

made.

Computation may in some cases be reduced by presum-

ming (when possible) the returns received by blocks of

array elements and applying the phase corrections for

focusing only to the sums.

In any event, computation may be substantially reduced

by integrating the phase-corrected returns in a bank of

doppler filters, with the FFT.

Some Relationships To Keep In Mind

• Minimum resolution requirements:

Road map details: 30 to 50 feet

Shapes: 1/5 to 1/20 of major dimension

• Achievable resolution

= 500 τ feet

τ = compressed pulse width

Required bandwidth = 1/

≈

R (for real array)

≈

R (for synthetic array)

(L = array length, same units as λ)

425

SAR Design

Considerations

n the last chapter, we saw how SAR takes advantage of

a radar's forward motion to synthesize a very long lin-

ear array from the returns received over a period of up

to several seconds by a small real antenna. We learned

how the array may be focused at virtually any desired range

and how the immense amount of computing required for

digital signal processing may be dramatically reduced

through doppler filtering techniques.

In this chapter, we will consider certain critical aspects

of SAR design which, if not properly attended to, may seri-

ously degrade the quality of the maps or perhaps even

render them useless: selection of the optimum PRF, side-

lobe reduction, compensation for phase errors resulting

from deviation of the radar bearing aircraft from a perfect-

ly straight constant-speed course—called motion compensa-

tion—and the minimization of other phase errors.

Choice of PRF

The PRF must be set low enough to avoid range ambi-

guities, yet high enough to avoid doppler ambiguities—or,

in terms of antenna theory, high enough to avoid problems

with grating lobes.

Avoiding Range Ambiguities. The maximum value of

the PRF is limited by the requirement that returns from the

ranges being mapped not be received simultaneously with

mainlobe returns from any other ranges. This requirement

may be readily met by setting the PRF so that the echo of

each pulse from the far edge of the real antenna's footprint

is received before the echo of the following pulse from the

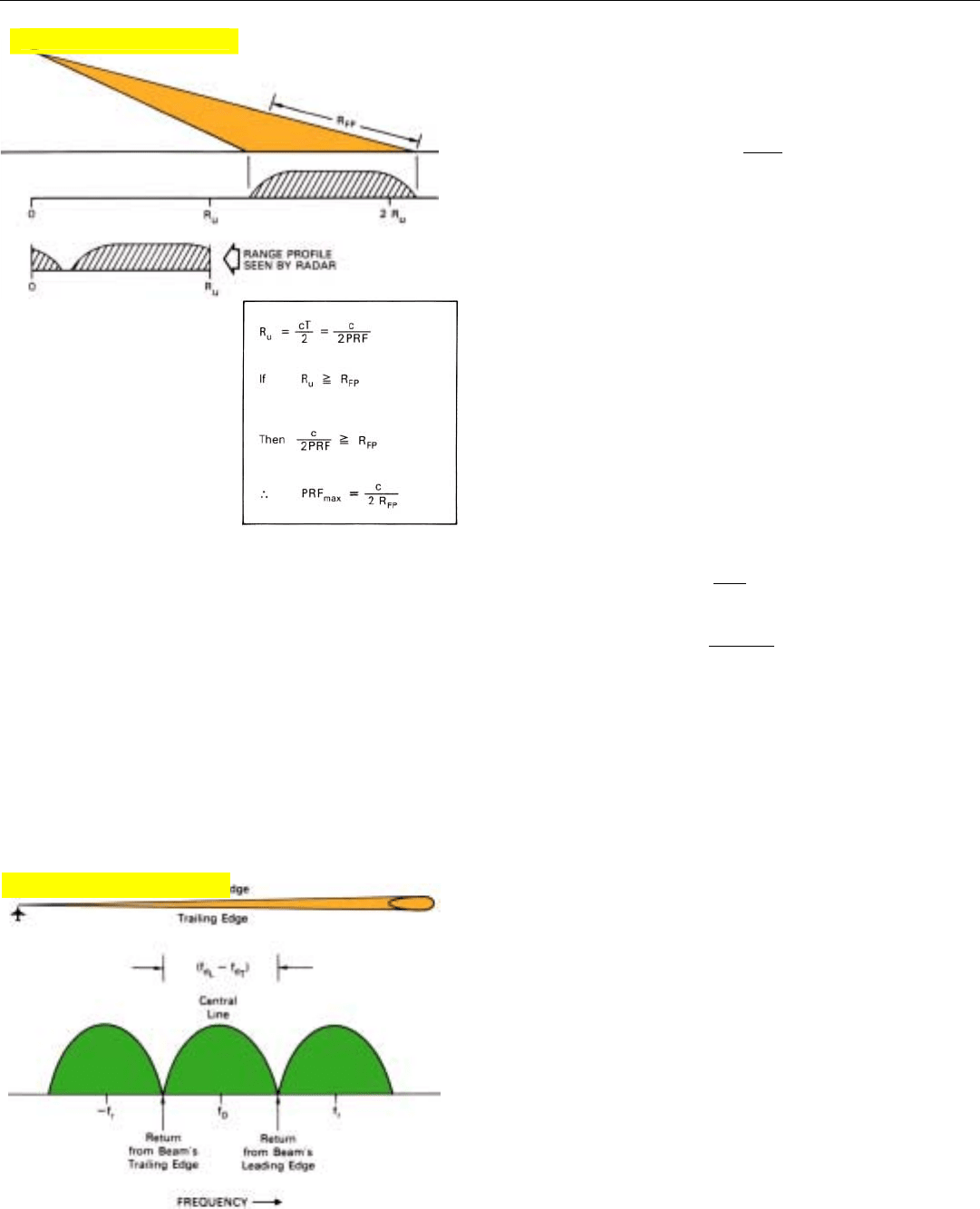
Find:

The maximum PRF a SAR radar can have and still avoid

range ambiguities under these conditions:

• Range segment being mapped may lie anywhere within

footprint of antenna beam.

• Slant range, R

FP,

spanning footprint = 20 nmi

• Speed of light = 162,000 nmi/sec

Calculation:

PRF

max

162,000

2 x 20

= 4050 Hz

PART VII High Resolution Ground Mapping & Imaging

426

near edge—in other words, so that the unambiguous range,

, is at least as long as the slant range, R

, spanning the

footprint (Fig. 1). That criterion will be satisfied if the PRF

is less than

PRF

max

where

c = speed of light (162,000 nmi/second)

= range spanning footprint of real antenna

1. Range ambiguities may be

avoided by making R

greater than the slant range

from the near edge to the

far edge of the real anten-

na’s footprint, R

2. To avoid doppler ambiguities, the PRF must exceed the differ-

ence between the doppler shifts at the leading and trailing

edges of the real antenna’s mainlobe.

Sample Computation of PRF

max

As you may be thinking, if only a small segment of R

being mapped, cannot higher PRFs in some cases be used?

Certainly. Within a narrow segment in the center of R

, for

instance, ambiguities may be avoided even with PRFs

approaching twice the maximum given by the above

expression.

Avoiding Doppler Ambiguities. The minimum PRF is

generally limited by the requirement that the “lines” of main-

lobe ground return must not overlap. To meet this require-

ment, the PRF must exceed the maximum spread between

the doppler frequencies of points on the ground at the lead-

ing and trailing edges of the mainlobe of the real antenna.

Therefore,

PRF

min

= f

– f

where f

and f

are the doppler frequencies at the main-

lobe's leading and trailing edges (Fig. 2).

In the case of a narrow azimuth beamwidth, the doppler

spread is approximately equal to 2 V

/ λ times the sine

Click for high-quality image