Genshiro Kitagawa. Introduction to Time Series Modeling (Введение в моделирование временных рядов)

Подождите немного. Документ загружается.

GENERATION OF GAUSSIAN WHITE NOISE 239

They showed that for p = 624, by taking A and B appropriately, the gen-

erated series has a period of length 2

19937

−1 and are distributed uni-

formly on the 623 dimensional space.

Different from these families of pseudo-random numbers that are

generated in software using certain algorithm s, hardware for generat-

ing physical (hardware) random numbers has a lso been developed. Such

hardware can be used whe n more precise random numbers are ne ces-

sary in a simulation, because random numbers generated in this way are

supposed to be free from any cycles or correlations.

16.2 Generatio n of Gaussian White Noise

A realization of G a ussian white noise is obtained by generating a se-

quence of random numbers that follows a normal distribution, na mely,

normal random numbers. The Box-Muller transform (Box and Muller

(1958)) for generating normal random numbers is well known. This

method applies the fact that, given two ind e pendent uniform random

numbers U

and U

on [0,1],

−2 lo gU

cos2

−2 lo gU

sin2

(16.6)

indepen dently follow the standard normal distribution N(0,1).

In practice, however, Marsaglia’s algorithm that follows c a n avoid

the explicit evaluation of sine and cosine functions a nd thus can generate

normal random numbers more efﬁciently.

1. Generate the uniform random numbers U

and U

2. Put V

= 2U

−1 and V

= 2U

−1.

3. Put S

= V

4. Return to Step (1), if S

≥ 1.

5. Put X

= V

−2 logS

and X

= V

−2 logS

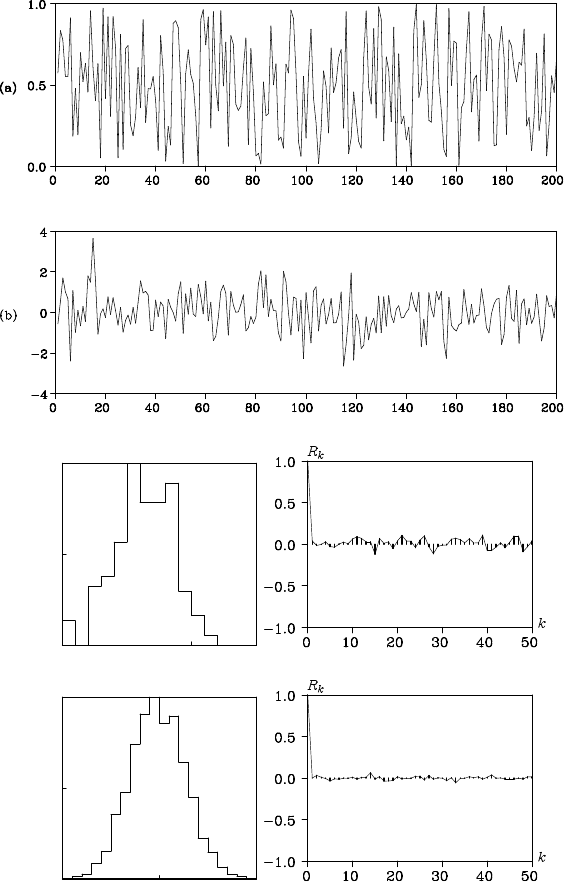
Figure 16.1 (a) shows 200 uniform random numbers generated by

the multiplicative congruence method of (16.1 ) with the initial value

= 1990103011. On the other hand, plo t (b) shows n ormal random

numbers (white noise) obtained with Ma rsaglia’s algo rithm using these

unifor m random numbers. Plot (c) depicts the histogram and the sample

autocorrelation function computed from those random numbers, whe re

the histogram looks somewhat different from the density of the normal

240 SIMULATION

Figure 16.1 Realizations, histograms and autocorrelation functions of uniform

random numbers and white noise.

SIMULATION USING A STATE-SPACE MODEL 241

distribution. Plot (d) shows th e histogram and the sample autocor rela-

tion function, respectively, when the number of realizatio ns is increa sed

to 2000. It can be seen that the histogra m resembles the normal density

and that the sample autocorrelation function approaches zero.

16.3 Simulation Using a Stat e -Space Model

Using the realizations of white noise introduced in the previous subsec-

tion, we can generate a time series that follows a given time series model.

This is called the simulation of the time series. Assume that the time se-

ries model is represented in the form of the state-space model :

= Fx

n−1

+ Gv

, (16.7)

= Hx

+ w

. (16.8)

Based on this state-space model, if the initial state vector x

, and

N realizations of k-dimensional Gaussian white n oise with mean 0 and

variance-covariance matrix Q, v

,.. ., v

, are given, the realizations of

the state vectors, x

,.. ., x

can be easily obtained by r e peatedly substi-

tuting them into the system model of (16.7). Further, if the realizations

of ℓ-dimensional Gaussian white noise with mean 0 and the variance-

covariance matrix R, w

,.. ., w

, are given, the time series y

,.. ., y

can

be generated by the obser vation model of (16.8).

A k-d imensional Gaussian white noise with mean 0 and variance-

covariance matrix Q ca n be obtained from k one- dimensional Gaussian

white noises generated by the method shown in the p revious subsec-

tion. Deﬁne a k-dimensional vector u

= (u

(1)

,···, u

(k)

)

, where u

( j)

is a

one-dimensional Gaussian white noise, then u

becomes a k-dimensional

Gaussian white noise with mean vector 0 and unit variance-covariance

matrix I

. Here, we assume that a k ×k lower triangular matrix L such

that Q = LL

can be obtained by the Cholesky d ecomposition of the

positive-deﬁnite symmetric matrix Q. Then, the k-dimensional vector v

deﬁned by

= Lu

(16.9)

satisﬁes

E(v

) = E(Lu

) = LE(u

= LI

= Q, (16.10)

showing that v

becomes a normal white noise with mean vector 0 and

the variance-covariance matrix Q.

242 SIMULATION

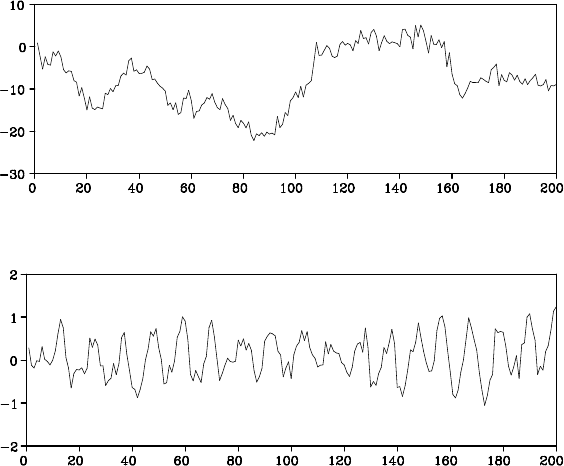
Figure 16.2: Simulation of a random walk model.

Figure 16.3: Simulation of an AR model.

Example (Simulation of a r andom walk model) Figure 1 6.2 sh ows

the results of the simulation f or the random walk model

= x

n−1

+ v

= x

+ w

, (16.11)

where the system n oise v

follows the normal distribution N(0,

/6)

and the observation noise w

is th e standard Gau ssian white noise that

follows N(0,1) and the initial state is x

= 0.

Example (Simulation of an AR model) Figure 16.3 shows the re-

sults of the simulation for the AR model with order 10 ﬁtted to the log-

arithms of the sunspot numbe r data. Since the state-space representation

for the AR model does not have any observation noise, we set R = 0.

Here, the initial state is set to x

= (0,... ,0)

and 400 time series are

generated. To remove the effects of the 0 initial state, the ﬁrst 200 ob-

servations are discarded and Figure 16.3 shows only the latter half of the

data.

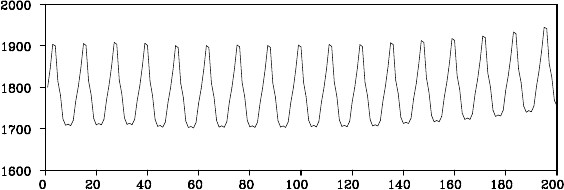
SIMULATION WITH NON-GAUSSIAN MODEL 243

Figure 16.4: Simulation of a seasonal adjustment model.

Example (Simulation of a seasonal adjustment model) Figure 16.4

shows the results of a simulation for the seaso nal adjustment model.

The model is shown in Figure 12.6 with the stationary AR componen t

= 2, m

= 1, m

= 2 and p = 12). As the initial state vecto r x

, the

vector x

0|N

is used for the smoothed estimate of the initial vector, which

is obtained from the actual seasonal data. A lthough the simulation of

the seasonal adjustment model resembles the actual tim e series shown

in Figure 1.1(d), it is evident that the tren d component of Figure 16.4 is

considerably different from that of Figure 1.1(d).

16.4 Simulation with the Non-Gaussian State-Space Model

The method of simulation for the state-space model presented in the pre-

vious section can be easily extended to the simulation of a non-Gaussian

time series mode l. Consider a non-Gaussian state-space model,

= Fx

n−1

+ Gv

, (16.12)

= Hx

+ w

, (16.13)

where v

and w

are not necessarily Gaussian and are distributed accord-

ing to the density functions q(v) and r(w), respectively.

For simplicity, it is assumed that the k componen ts of v

and the ℓ

components of w

are mu tually independent. To simulate the above non-

Gaussian state-space model, it is nec essary to develop a method of gen-

erating realizations of white n oise that follow an arbitrarily deﬁned den -

sity function p(x). For some speciﬁc distributions, such as the Cauchy

distribution, the

distribution and the two-sided exponential (Laplace)

distribution, they can be generate d by a transformation of the uniform

244 SIMULATION

random numbers or the normal random numbers. In the following sub-

section, some examples are given.

16.4.1

distribution

The

distribution w ith j degre es of freedom can be expressed a s

= X

+ ···+ X

, (16.14)

where X

,···, X

are n ormal random variables. Therefore, to generate

random numbers that follow the

distribution, we initially generate j

normal random num bers and then obtain

using equation (16.14). In

particular, exponential random numbers are obtained by puttin g j = 2.

Further, by deﬁning Z = log

, we obtain the double exponential ran-

dom numbers. Note that an exponential random number can be obtained

from a uniform ran dom nu mber directly by setting

v = −log u, (16.15)

given the uniform random number u. Then, the double exponential ran -

dom number is efﬁciently obtained by

v = lo g(−log u). (16.16)

16.4.2 Cauchy distribution

The density function of the Cauchy distribution that was u sed for the

non-Gaussian model in Chapter 14 is given by

p(x) =

+ 1)

. (16.17)

To generate Cauchy random numbers, we generate a unifo rm random

number on [0,1), and for u 6= 0.5, deﬁne v by

v = tan

u. (16.18)

16.4.3 Arbitrary distribution

In general, random numbers that follow an arbitrary density function

f (x) can be generated by using the inverse function of the distribution

function. The distribution function is a mono tone increasing function

deﬁned by

F(x) =

−∞

f (t)dt, (16.19)

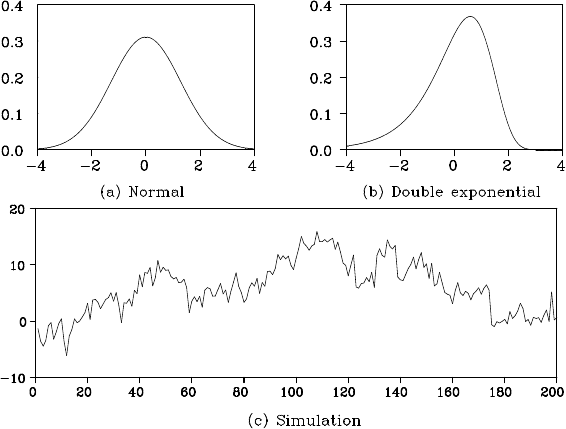
SIMULATION WITH NON-GAUSSIAN MODEL 245

Figure 16.5: Density functions of system noise and the results of the simulation.

which satisﬁes 0 ≤ F(x) ≤ 1, F(−∞) = 0, and F (∞) = 1. He re, if

we obtain an inverse function G(y) ≡ F

−1

(y), 0 ≤ y ≤ 1, that satisﬁes

F(G(y)) = y, then G is a function from (0,1 ) to (−∞,∞). Therefore,

if u is a uniform rand om number on [0, 1), v = G(u) becomes a random

number that follows the density function f (v). Applying this method, w e

can generate random numbers that f ollow various distributions by using

the density functions discussed in Ch apter 4.

Example (Trend model wit h double-exponentia l noise) Figu re

16.5 shows the results of the simulation, which were obtained by re-

placing the system noise of th e random walk model in Figure 16.2 by

= r

, where r

denotes a double exponential random number and

= 0.57722 deno te s the Euler constant.

For comparison, plots (a) and (b) show the density functions of the

normal distribution used in Figure 16.2 and the double exponential dis-

tribution. Even though the two density functions have the same mean and

the same variance, they have different shapes, and so different simulation

results are obtained.

As shown in Figure 16.2, simulation with the density given in plot

(a) yields symmetric movement around the trend. On the other hand, in

246 SIMULATION

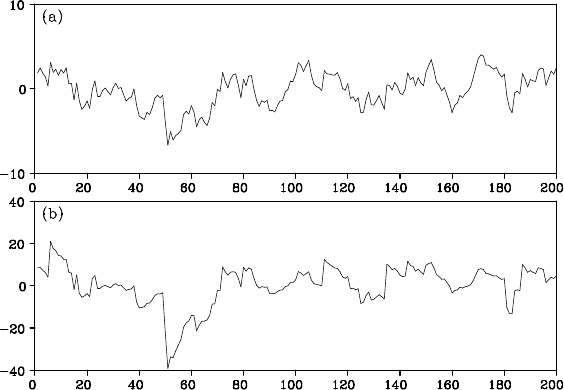
Figure 16.6 Simulation of an AR model with different noise distributions: (a)

normal distribution, (b) Cauchy distribution.

plot (c) obtain e d by usin g the density in plot (b), the behavior around

the trend shows asymmetric upward and downward tendencies. We can

observe such typical asymmetric behavior of time ser ie s freq uently in

ﬁnancial data.

Example (AR models with Gaussian and non-Gaussian noise) Fig-

ure 16.6 shows the simulation results for the AR model of ﬁrst order:

= 0.9y

n−1

+ v

. (16.20 )

Here, in plots (a) and (b), v

is assumed to be the standard no rmal dis-

tribution N(0, 1) and the Cauc hy distribution C(0,1), respectively. Even

though the AR models are of the same order and have the same AR co-

efﬁcients, the two time series in plots (a) an d (b) appear quite different,

because the distributions of the noise v

are different. In particular, in

plot (b), the time serie s occasionally shows big jumps, and the w idth of

the ﬂuctuation is, as a whole, more than twice as large as that of plot (a).

SIMULATION WITH NON-GAUSSIAN MODEL 247

Problems

1. Assume that U and V are uniform random n umbers deﬁned on [0,1].

What distribution does W = U +V follow?

2. In the simulation of an AR model y

= ay

n−1

+ v

, v

∼ N(0, 1), we

usually generate m +n data elements and discard the initial m realiza-

tions. How large should m be?

3. Show a method of simulating future values based on observations up

to the present time.