Гельруд Я.Д. Методы принятия решений

скомпенсирован за счет другого; например, малая продуктивность – за счет

низкой стоимости и т.д. Это, как правило, несправедливо.

Вспомним «критерий для оценки человека», полушутя полусерьезно

предложенный когда-то Львом Толстым. Он имеет вид дроби, в числителе

которой стоят действительные достоинства человека, а в знаменателе – его

мнение о себе. С первого

взгляда такой подход может показаться

логичным. Но представим себе человека, имеющего незначительные

достоинства, но совсем не обладающего самомнением. По критерию Л.И.

Толстого такой человек должен иметь бесконечно большую ценность, с

чем уж никак согласиться нельзя…

К подобным парадоксальным выводам может привести (и нередко

приводит) использование обобщенного показателя в виде

дроби, где, как

говорят, все, что «за здравие», – в числителе, все, что «за упокой», – в

знаменателе.

Нередко применяется и другой, чуть более замысловатый, способ

составления обобщенного показателя эффективности – он представляет

собой «взвешенную сумму» частных показателей, в которую каждый из

них F

i

входит с некоторым «весом» а

i

, отражающим его важность:

F = а

1

F

1

+ а

2

F

2

+… (1)

(для тех показателей, которые желательно увеличить, веса берутся

положительными, уменьшить – отрицательными).

При произвольном назначении весов а

1

, а

2

,… этот способ ничем не

лучше предыдущего (разве тем, что обобщенный критерий не обращается

в бесконечность). Его сторонники ссылаются на то, что и человек,

принимая компромиссное решение, тоже мысленно взвешивает все «за» и

«против», приписывая больший вес более важным для него факторам.

Это, быть может, и так, но, по-видимому, «весовые

коэффициенты», с

которыми входят в расчет разные показатели, не постоянны, а меняются в

зависимости от ситуации.

Поясним сказанное элементарным примером. Человек выходит из

дому, чтобы ехать на работу, боится опоздать, и размышляет: каким

транспортом воспользоваться? Трамвай ходит часто, но идет долго;

автобус – быстрее, но с большими интервалами. Можно взять такси, но это

дорого.

Перед нами типичная (намеренно упрощенная) задача исследования

операций с двумя критериями (показателями).

Первый – среднее

ожидаемое время опоздания Т, которое хотелось бы сделать

минимальным. Второй – ожидаемая стоимость проезда S; ее тоже

желательно сделать минимальной. Но эти два требования, как мы знаем,

несовместимы, поэтому человек должен принять компромиссное,

приемлемое по обоим критериям, решение. Возможно, он при этом

подсознательно взвешивает все «за» и «против», пользуясь чем-то

вроде

обобщенного показателя:

F = а

1

Т + а

2

S ⇒ min. (2)

Но беда в том, что весовые коэффициенты а

1

, а

2

никак нельзя считать

постоянными. Они зависят как от самих величин Т и S, так и от

обстановки. Например, если человек недавно уже получил выговор за

опоздание, коэффициент при Т у него, вероятно, увеличится, а на другой

день после получки, вероятно, уменьшится коэффициент при S. Если же

назначать (как это обычно и делается) веса

а

1

, а

2

произвольно, то, по

существу, столь же произвольным будет и вытекающее из них

«оптимальное» решение.

Здесь мы встречаемся с очень типичным для подобных ситуаций

приемом – «переносом произвола из одной инстанции в другую». Простой

выбор компромиссного решения на основе мысленного сопоставления

всех «за» и «против» каждого решения кажется слишком произвольным,

недостаточно «

научным». А вот маневрирование с формулой, включающей

(пусть столь же произвольно назначенные) коэффициенты а

1

, а

2

,…, –

совсем другое дело. Это уже «наука»! По существу же никакой науки тут

нет, и нечего обманывать самих себя.

Нечего надеяться полностью избавиться от субъективности в задачах,

связанных с выбором решений. Даже в простейших, однокритериальных

задачах она неизбежно присутствует, проявляясь хотя бы в выборе

показателя эффективности и математической модели явления. Тем

более

неизбежна субъективность (грубо говоря, произвол) при выборе решения в

многокритериальной задаче. Правда, бывают редкие случаи, когда

достаточно ознакомиться со значениями всех показателей для каждого

варианта, чтобы сразу стало ясно, какой из них выбрать. Представим себе,

например, что некий вариант решения имеет преимущество над другими

по всем показателям; ясно, что

именно его следует предпочесть. Но

гораздо чаще встречаются случаи, когда ситуация неочевидна: один из

показателей тянет в одну сторону, другой – в другую. При этом всегда

полезно провести дополнительные расчеты, пользуясь, быть может, даже

формулами типа (1), но, не доверяя им слепо, а сохраняя к ним

критическое отношение.

Выходит, что математический аппарат

не может нам ничем помочь

при решении многокритериальных задач? Отнюдь нет, он может помочь, и

очень существенно. Прежде всего, он позволяет решать прямые задачи

исследования операций, т.е. для любого решения х находить значения

показателей эффективности F

1

, F

2

,…, сколько бы их не было (кстати, для

прямых задач многокритериальность – не помеха).

1

И во-вторых, что

особенно важно, он помогает «выбраковать» из множества возможных

решений Х заведомо неудачные, уступающие другим по всем критериям.

1

) Под прямыми задачами Е.С.Вентцель[2] понимает задачи, которые отвечают на

вопрос: что будет, если в заданных условиях принять некоторое решение

х

∈

Х?

Например, чему будет при этом равен показатель эффективности или их набор.

Обратные задачи отвечают на вопрос: как выбрать решение

х, для которого показатель

эффективности F достигнет экстремального значения

.

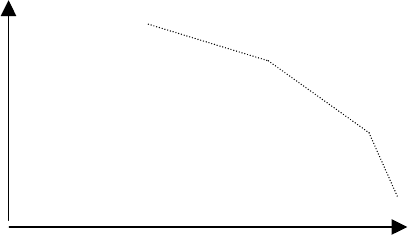
Покажем, как это делается. Пусть имеется многокритериальная задача

исследования операций с k критериями F

1

, F

2

,…, F

k

. Для простоты

предположим, что все эти величины желательно максимизировать.

Пусть в составе множества возможных решений есть два решения х

1

, х

2

такие, что значения всех критериев F

1

, F

2

,…, F

k

для первого решения

больше или равны соответствующим критериям для второго решения,

причем хотя бы один из них действительно больше. Тогда из состава

множества Х решение х

2

вытесняется ( говорят «доминируется») решением

х

1

. В результате такой процедуры отбрасывания заведомо невыгодных

решений во множестве Х сохраняются только эффективные

(«оптимальные по Парето» или «паретовские») решения, характерные

тем, что ни для одного из них не существует доминирующего решения.

4.2. Оптимальность по Парето.

Проиллюстрируем прием выделения паретовских решений на примере

задачи с двумя критериями: F

1

и F

2

(оба требуется максимизировать).

Множество Х состоит из конечного числа n возможных решений х

1

, х

2

,…,

х

n

. Каждому решению соответствуют определенные значения показателей

F

1

, F

2

; будем изображать решение точкой на плоскости с координатами F

1

,

F

2

и занумеруем точки соответственно номеру решения (рис. 8).

F

2

. .2

.1 .4 .5

.7 .3 .8 .9

.6 .10

.17 .16 .15 .14 .12

.18 .19 .11

.20 F

1

Рис. 8. Оптимальность по Парето.

Очевидно, из всего множества Х эффективными (доминирующими)

будут только решения х

2

, х

5

, х

10

, х

11

, лежащие на правой верхней

границе области возможных решений (см. точки, соединенные

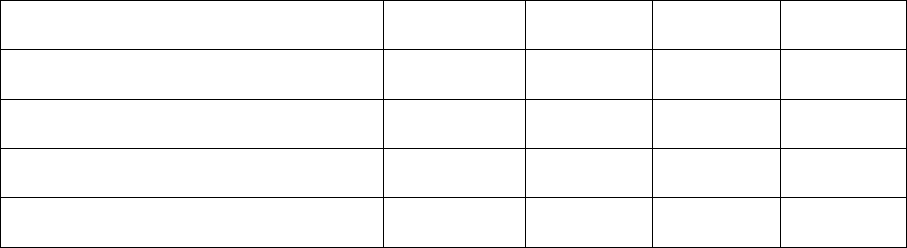
пунктиром), причем х

11

– наилучшее по критерию F

1

, х

2

– по критерию

F

2

. Дело лица, принимающего решение, выбрать тот вариант, который для

него предпочтителен и «приемлем» по обоим критериям.

Аналогично строится множество эффективных решений и в случае,

когда показателей не два, а больше (при этом геометрическая

интерпретация теряет наглядность, но суть дела сохраняется).

Рассмотрим макроэкономическую модель Финляндии, построенную в

70-х годах. Качество

решений оценивалось по четырем критериям:

С

!

– увеличение валового национального продукта (в %);

С

2

– уменьшение инфляции (в %);

С

3

– уменьшение безработицы (в %);

С

4

– уменьшение дефицита внешней торговли (млрд. фин. марок).

В табл.13 приведены три различных варианта экономической

политики.

Таблица 13. Значения критериев вариантов экономической политики

Вариант решения С

!

С

2

С

3

С

4

1 – 2,74 8,16 3,28 2,24

2 0,57 9,00 2,81 5,27

3 1,81 8,88 2,64 6,54

Наилучшие решения 7,18 8,16 1,88 1,21

В нижней строке табл.13 приведены наилучшие значения каждого из

критериев, которые можно получить, если оптимизировать по одному

критерию, не обращая внимания на другие. Наилучшие значения по всем

критериям одновременно не достижимы. Легко видеть, что приведенные

альтернативы являются точками множества Парето в четырехмерном

пространстве критериев. Действительно, первый вариант дает наименьшее

значение

инфляции и дефицита внешней торговли, но отрицательный

прирост ВНП и большую безработицу. Третий вариант лучший по росту

ВНД и уровню безработицы, но худший по дефициту внешней торговли.

Эти противоречия отражают типичный характер вариантов

многокритериальных решений.

Множество эффективных решений легче обозримо, чем множество Х.

Что касается окончательного выбора решения, то он по-прежнему остается

прерогативой человека. Только человек

, с его непревзойденным умением

решать неформальные задачи, принимать компромиссные решения (не

строго-оптимальные, но приемлемые по ряду критериев) может взять на

себя ответственность за окончательный выбор.

Однако сама процедура выбора решения, будучи повторена

неоднократно, может послужить основой для выработки некоторых

формальных правил, применяемых уже без участия человека. Речь идет о

так называемых «эвристических» методах выбора решений. Предположим,

что опытный менеджер (или, еще лучше, их группа) многократно выбирает

компромиссное решение в многокритериальной задаче исследования

операций, решаемой при разных условиях α. Набирая статистику по

результатам выбора, можно, например, разумным образом подобрать

значения «весов» а

1

, а

2

,… в формуле (1), в общем случае зависящие от

условий α и самих показателей F

1

, F

2

,…, и воспользоваться таким

обобщенным критерием для выбора решения, на этот раз уже

автоматического, без участия человека. На это иногда приходится идти в

случаях, когда времени на обдумывание компромиссного решения нет

(например, в условиях боевых действий), или же в случае, когда выбор

решения передается автоматизированной системе управления.

В некоторых случаях

очень полезной оказывается процедура выбора

решения в диалоговом (или интерактивном) режиме, когда компьютер,

произведя расчеты, выдает лицу, управляющему операцией, значения

показателей F

1

, F

2

,…, а это лицо, критически оценив ситуацию, вносит

изменения в весовые коэффициенты (или иные параметры управляющего

алгоритма) и расчеты повторяются.

Часто применяется на практике способ свести многокритериальную

задачу к однокритериальной – это выделить один (главный) показатель F

1

и стремиться его обратить в максимум, а на все остальные F

2

, F

3

,…

наложить только некоторые ограничения, потребовав, чтобы они были не

меньше каких-то заданных f

2

, f

3

,… Например, при оптимизации плана

работы предприятия можно потребовать, чтобы прибыль была

максимальной, план по ассортименту – выполнен или перевыполнен, а

себестоимость продукции – не выше заданной. При таком подходе все

показатели, кроме одного – главного (прибыль), переводятся в разряд

заданных условий α. Некоторый произвол в назначении границ f

2

, f

3

,…,

разумеется, при этом остается; поправки в эти границы тоже могут быть

введены в диалоговом режиме.

Существует еще один путь построения компромиссного решения,

который можно назвать методом последовательных уступок.

Предположим, что показатели F

1

, F

2

,… расположены в порядке

убывающей важности. Сначала ищется решение, обращающее в максимум

первый (важнейший) показатель F

1

= F

1

*. Затем назначается, исходя из

практических соображений, с учетом той точности, с которой нам

известны входные данные, некоторая «уступка» ∆F

1

, которую мы согласны

сделать для того, чтобы максимизировать второй показатель F

2

. Наложим

на показатель F

1

ограничение: он должен быть не меньше, чем F

1

* – ∆F

1

, и

при этом ограничении ищем решение, обращающее в максимум F

2

. Далее

снова назначаем «уступку» ∆F

2

, ценой которой можно максимизировать

F

3

, и т.д. Такой способ построения компромиссного решения хорош тем,

что здесь сразу видно, ценой какой «уступки» в одном показателе

приобретается выигрыш в другом и какова цена этого выигрыша.

Так или иначе, при любом способе ее постановки, задача

обоснования решения по нескольким показателям остается не до конца

формализованной, и окончательный выбор решения всегда определяется

волевым актом лица, принимающего решения (ЛПР

). Дело исследователя –

предоставить в распоряжение ЛПР данные, помогающие ему сделать

выбор не «вслепую», а с учетом преимуществ и недостатков каждого

варианта решения.

4.3. Метод идеальной точки.

Можно рекомендовать еще метод идеальной точки, который состоит в

отыскании среди паретовских решений ближайшего к точке утопии,

задаваемой ЛПР. Формулируется цель в виде желаемых

значений

показателей, и часто выбирается сочетание наилучших значений всех

критериев F

1

*, F

2

*,… (обычно эта точка не реализуется при заданных

ограничениях, поэтому ее и называют точкой утопии). Лучшим считается

решение х, обращающее в минимум сумму квадратов отклонений значений

всех критериев F

i

(х) от их наилучших значений F

1

*, F

2

*,…

Пример 6. Пусть множество допустимых планов описывается

системой неравенств:

Заданы две целевые функции

⎪

⎩

⎪

⎨

⎧

≤+

≤≤

.62

,20

,40

ух

у

х

F

1

=х + у +2,

F

2

=х – у + 6,

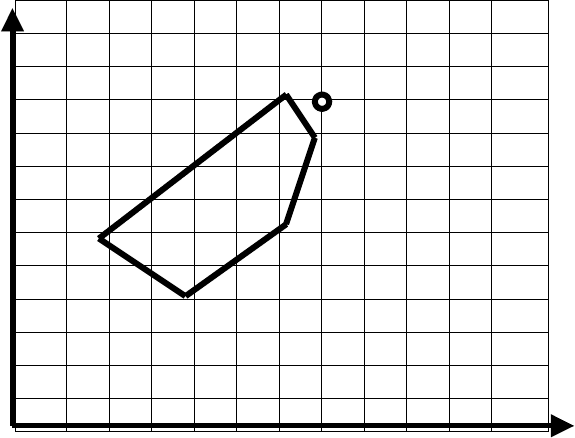
которые необходимо максимизировать. На рис. 9 представлено множество

возможных решений в пространстве критериев.

F

2

В М

С

А D

Е

F

1

Рис.9.

Отрезок ВС является множеством точек, оптимальных по Парето.

Действительно, в точке В F

2

принимает максимальное значение F

2

=10

(F

1

=6), а в точке С F

1

принимает максимальное значение F

1

=7 (F

2

=9).

Точка утопии М имеет координаты (7,10).

Идеальная точка – точка на отрезке ВС, ближайшая к точке утопии М. Эта

точка имеет координаты F

1

=6.5, F

2

=9.5, следовательно

х + у +2=6.5,

х – у + 6=9.5,

откуда х=4, у=0.5.

Тема 5. Управление организационными системами.

5.1. Распределение ресурсов.

Рассмотрим простейшую двухуровневую организационную систему,

состоящую из Центра и некоторого числа n однотипных Элементов

(в данном случае Потребителей). Центр на основании заявок Потребителей

(в размере s

i

) должен распределить имеющийся в его распоряжении ресурс

(в количестве R). Если (ситуация дефицита), то необходимо

определить по некоторому правилу х

i

– объемы ресурса, выделяемых i-му

Потребителю.

Rs

i

>

∑

,

1

n

i

=

5.1.1. Механизм прямых приоритетов.

Наряду с размерами заявок Центр учитывает приоритет каждого

Потребителя, который задается числом А

i

. В соответствие с механизмом

прямых приоритетов распределение осуществляется по правилу

(3)

{

}

minx ,,

iiii

sAs

γ

=

где γ – общий для всех потребителей параметр – определяется из условия

(4)

(весь ресурс распределяется без остатка).

,

1

Rх =

∑

Самый простой случай возникает при равенстве всех приоритетов.

Тогда, очевидно, х

i

= γs

i

, откуда γ=R/

(все заявки пропорционально «урезаются» путем умножения на γ).

Пример 7. Пусть 5 Потребителей подали заявки в размере 5,8,12,7 и 8.

Имеющийся в распоряжении Центра ресурс R=32. Как распределить этот

ресурс при равенстве приоритетов?

Определяем коэффициент

γ=R/ =32/40=0,8.

n

i

=

i

1

∑

=

n

i

s

1

∑

i

s

=

n

Решение находим в виде х

i

= γs

i

:

х

1

= 0,8×5=4, х

2

=0,8×8=6,4, х

3

=0,8×12=9,6, х

4

= 0,8×7=5,6, х

5

=0,8×8=6,4.

Отметим недостатки этого метода при равенстве приоритетов.

Гельруд Я.Д. Методы принятия решений

Подождите немного. Документ загружается.