Гельруд Я.Д. Методы принятия решений

Подождите немного. Документ загружается.

понятия, как критические работы, резервы времени и т.п.; в

состязательных задачах (теория игр) – понятия ход, платежная матрица,

чистые и смешанные стратегии и т.д…

При постановке задачи и ее моделировании необходимо прежде

всего оценить, какой из формулировок принципа экономичности

соответствует данная ситуация принятия решения.

Принцип экономичности может формулироваться двояко

- заданных целей (результатов) достигнуть при минимальных

затратах;

- при заданных пределах затрат достигнуть цели в максимальной

степени (достичь максимума результата).

Принцип экономичности в первой формулировке иногда называют

«принципом экономии средств», во второй – «принципом максимального

эффекта». Если задача формулируется по «принципу максимального

эффекта», то целевая функция являет собой условие достижения цели

(цель – максимум результата), остальные математические выражения,

входящие в модель, – суть условия-ограничения.

Часто принцип экономичности формулируют так:

«достигнуть максимальной степени реализации цели (максимального

результата) при минимальных затратах». Такое определение неверно,

внутренне противоречиво с содержательной точки зрения и ведет к

постановке математически неразрешимой задачи.

Кроме того, у руководителей возникает искушение

оптимизировать решение задачи по нескольким критериям. Например,

следующим образом: «найти такое решение, которое обеспечило бы

максимум размера торгового оборота при минимуме годовых издержек

производства и минимуме капитальных вложений».

При всей внешней привлекательности и кажущейся естественности –

такая постановка ведет к неразрешимой задаче. Желательно, как правило,

стремиться так формулировать задачи, чтобы при множественности целей

и ограничений, критерий оптимизации решения (а, стало быть, и целевая

функция) был один. Следует отметить, что в ряде сложных

организационных задач возникает проблема многокритериальности.

Некоторые подходы к постановке и решению такого рода задач будут

рассмотрены в Теме 4.

Изложенное выше еще раз подтверждает

важность правильного

обоснования цели и критерия эффективности при постановке задачи, так

как при этом определяется и выбор соответствующего варианта

формулировки принципа экономичности.

Важным достижением теории и практики применения

математического моделирования в решении организационных задач

является выработка типологии задач.

Индивидуальные различия задач относятся к их содержанию, а

сходство определяется их формой.

Любая задача обладает как

содержанием, так и формой. Под формой понимается структура задачи, то

есть состав ее переменных и постоянных и их взаимосвязь. Содержание же

определяется природой этих величин. Мы отделяем форму задачи от ее

содержания с помощью процесса абстракции. Язык, на котором

описывается форма задачи (условия задачи, абстрагированные от их

содержания), является языком математики. При необозримом числе

конкретных ситуаций принятия решений большинство задач может быть

отнесено к определенным типам с точки зрения их формы и, тем самым, к

определенным типам математических средств их описания и решения. Это

и позволило осуществить классификацию задач организационного

управления, приняв в качестве классификационного признака не

содержательные особенности задач, а формальные, иными словами,

общность задач, в конечном счете, определить типами математических

моделей, в наибольшей мере соответствующими формам этих задач, то

есть наилучшим образом описывающими условия этих задач и

обладающими алгоритмическими средствами их решения (уместно

отметить, что подобная классификация в свою очередь дала мощный

импульс развитию исследований в соответствующих областях прикладной

математики).

Различают задачи следующих основных классов:

1) распределения,

2) управления запасами,

3) замены,

4) массового обслуживания,

5) упорядочения и координации (управления проектами),

выбора маршрута,

7) состязательные,

8) поиска,

9) комбинированные.

Этим классам соответствуют определенные типы математических

моделей, а иногда и соответствующие направления прикладной

математики, такие как математическое программирование, теория

управления запасами, теория массового обслуживания, сетевое

моделирование, теория игр и т.п. (см. раздел 4 «Математики»). В каждом

классе могут быть выделены подклассы, в которых в

свою очередь можно

выделить виды и подвиды.

Всякая классификация является упорядочением, а потому весьма

информативна. Вспомним известную классификацию животного мира из

биологии. Теперь представим, что некий биолог рассматривает некое ранее

ему не известное существо и обнаруживает, что оно может быть отнесено

к классу млекопитающих. Какой огромный объем информации об этом

животном дает ему этот факт! Точно так же, управляющий,

сталкивающийся с ситуацией принятия решения, знакомясь с проблемой и

пытаясь сформулировать задачу, обнаруживает, что по форме эта задача

может быть отнесена, например, к задаче линейного программирования.

Теперь он способен дать четкую постановку задачи, теперь он

знает, какая информация и в каком виде потребуется для решения этой

задачи, какую информацию он может получить в результате решения

(например, кроме оптимальных объемов

производства определенных

видов продукции, еще и объективно обусловленные оценки ресурсов,

границы устойчивости оптимального решения и т.п.).

Теоретические концепции разработки управленческих решений с

применением методов математического моделирования и значительный

продуктивный опыт их применения на практике позволили создать

понятийный и терминологический аппарат для четкого описания

постановок задач не только на модельном

, но и на вербальном уровне.

Такие понятия как цели, контролируемые и неконтролируемые

переменные, параметры, ограничения, критерий эффективности, целевая

функция, область допустимых решений, оптимальное решение и т.п., –

стали неотъемлемой частью профессионального языка менеджеров, в

существенной мере влияя на их способ мышления.

Таким образом, включение математического моделирования в

профессиональный арсенал методов

и средств управляющего позволяет не

только повысить эффективность принимаемых им решений благодаря

непосредственному использованию математических моделей и методов

для решения конкретных управленческих задач, но и оснащает его

понятийными и терминологическими средствами и принципами

формулирования этих задач, тем самым способствуя выработке

профессионального образа и языка мышления.

1.3. Декомпозиция управленческого решения.

Разработка управленческого решения – сложный многоэтапный

процесс. Существует много предложений по декомпозиции этого процесса

на этапы и процедуры. Наиболее характерным является выделение

следующих этапов:

1) постановка задачи (или формулировка проблемы),

2) построение математической модели,

3) нахождение решения,

4) анализ модели и решения,

5) подстройка (уточнение) модели и нахождение уточненного

решения.

После принятия окончательного решения приступают к его

осуществлению.

Отметим особую важность первого этапа. Постановка задачи требует

правильного определения целей, границ влияния решений (т.е. границ

системы, с позиций которой будет приниматься решение), критерия

оценки вариантов решений. Именно на этом этапе системный подход

должен быть воплощен в максимальной степени.

Второй

этап – построение модели – по сути должен представлять

собой «перевод» на язык математики постановки задачи, выполненной на

первом этапе на вербальном уровне.

На третьем этапе посредством соответствующих алгоритмов

математические модели позволяют «проигрывать» различные варианты

управленческих решений («сжимать время»), производить анализ

вариантов и выбор наиболее целесообразного. Во многих случаях

нахождение лучшего варианта

сводится к решению математической

задачи, то есть к определению таких допустимых значений

контролируемых переменных, которые обеспечивают оптимальное

значение критерия эффективности решения, иными словами, находится

управленческое решение, реализация которого позволяет достигнуть цели

наилучшим способом или в наибольшей степени с позиций интересов

системы в целом.

Перед тем, как принимать решение, следует тщательно продумать его

цель. Для кого принимаемое решение должно быть наилучшим? Ведь

благо для одного лица (подразделения, предприятия) может быть во вред

другому. Поэтому понятие «

наилучший вариант действий» относительно,

оно жестко связано с тем, для кого и с какой целью принимается.

Человек, фактически осуществляющий выбор наилучшего варианта

действий, называется лицом, принимающим решения (ЛПР).

Варианты действий называют альтернативами. Альтернативы бывают

независимыми и зависимыми. Независимыми являются те альтернативы,

любые действия с которыми не влияют на качество других

альтернатив.

При зависимых альтернативах оценки одних из них оказывают влияние на

качество других. Так, при планировании развития города решение о

сохранении исторического центра влечет за собой рассмотрение всех

вариантов его реализации. Кроме того, существуют задачи, где

альтернативы появляются после принятия основных решений (задачи с

конструируемыми альтернативами).

Показатели привлекательности вариантов решений

для участников

процесса выбора называются критериями оценки альтернатив. На

сложность задач принятия решений влияет количество критериев. При

небольшом числе критериев (два-три) задача сравнения альтернатив

достаточно проста, качества по критериям могут быть непосредственно

сопоставлены и выработан компромисс. При большом числе критериев

задача выбора становится очень сложной, подходы к ее решению

рассмотрим в теме 4.

Каждой альтернативе в общем случае соответствует несколько

исходов, причем вероятность этих исходов может быть известна (эта

ситуация определяется как принятие решения в условиях риска), и

неизвестна (принятие решения в условиях неопределенности). При

моделировании задач принятия решений без учета риска и

неопределенности (каждой альтернативе соответствует один исход)

используются детерминированные модели исследования операций (см. [5],

темы 4-15).

Итак, чтобы найти наилучшее решение, следует:

• Определить цель решения.

• Определить возможные альтернативы решения

проблемы.

• Определить возможные исходы каждого решения.

• Оценить каждый исход.

• Выбрать наилучшее решение на основе поставленной цели.

Рассмотрим реализацию вышеперечисленных этапов на небольшом

примере.

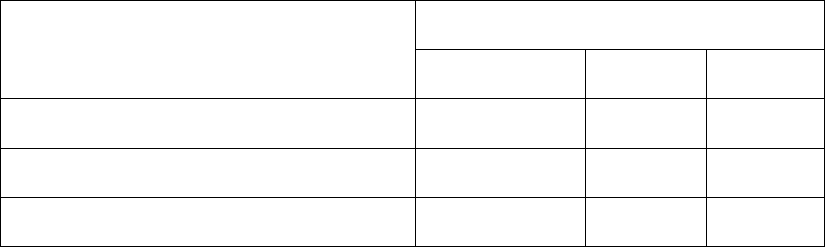
Пример 1. Отдел маркетинга представил своему руководству данные

об ожидаемом объеме сбыта некоторого товара при трех вариантах цены.

Таблица 1.

Возможная цена за единицу

Предполагаемый объем продаж при

данной цене (единиц в год)

8,00 8,60 8,80

Оптимистический прогноз

16000 14000 12500

Наиболее вероятный 14000 12500 12000

Пессимистический прогноз 10000 8000 6000

Пусть постоянные затраты составляют 40000 руб., переменные – 4

руб. за единицу.

Необходимо определить оптимальную цену, при которой будет

получена наибольшая прибыль. Мы имеем три альтернативы – три

варианта цены, и для каждой альтернативы по три возможных исхода –

различные годовые объемы продаж. Для каждого исхода рассчитаем

прибыль (цена минус переменные затраты умножить на объем продаж,

постоянные затраты пока не учитываем).

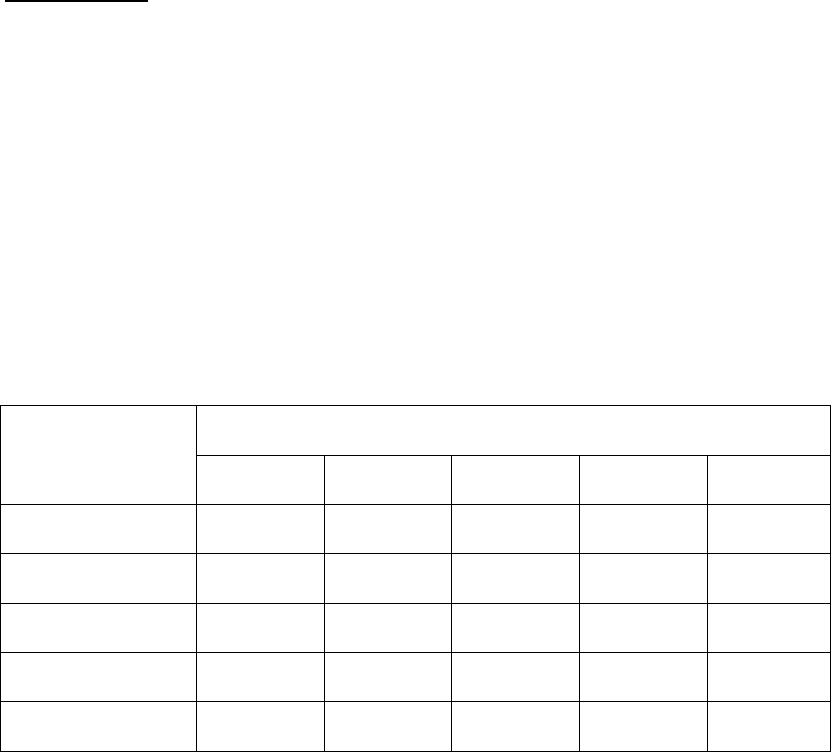
Таблица 2.

Возможная прибыль за единицу

Общая прибыль за год

(без учета постоянных затрат)

4,00 4,60 4,80

Оптимистический прогноз 64000 64400 60000

Наиболее вероятный 56000 57500 57600

Пессимистический прогноз 40000 36800 28800

Таким образом, на данном этапе оценка возможных исходов свелась к

расчету прибыли, получаемом при каждом варианте цены.

Теперь, на заключительном этапе принятия решения необходимо

выбрать оптимальное решение. Если ориентироваться на наиболее

вероятный объем продаж, то наибольшая прибыль 57600 будет получена

при цене 8,80, однако, следует заметить, что при цене 8,60 прибыль почти

такая

же (57500), зато при оптимистическом и пессимистическом прогнозе

существенно больше (на 4400 и 8000 соответственно). Если же принять во

внимание постоянные расходы, то только при цене 8,00 фирма не потерпит

убытков при худшем исходе, тогда как при другой цене возможны

существенные убытки (3200 при цене 8,60 и 11200 при цене 8,80).

Какое решение следует принять, зависит от поставленных

целей и

условий, в которых оно принимается (степень определенности

информации, отношение к риску и т.п.).

Тема 2. Правила принятия решений.

2.1. Правила принятия решений в условиях неопределенности

(без использования численных значений вероятностей исходов –

правила максимакса, Вальда, Сэвиджа, Лапласа).

Рассмотрим правила принятия решений в условиях неопределенности

на небольшом примере.

Пример 2. Пусть себестоимость пирожного в нашей кондитерской

составляет 7 руб., свеженькое продаем за 13 руб., а невостребованное за

день сдаем на свиноферму за 3 руб. Сколько пирожных надо производить

в день, если известно лишь, что спрос на них составляет от 1 до 5?

Составим таблицу возможных доходов, расположив построчно наши

альтернативы (производить от 1 до 5 пирожных), а

в столбцах исходы

(продать от 1 до 5), имея в ввиду, что доход от продажи одного пирожного

составляет 6 руб., а потери при не продаже составляют 4 руб.

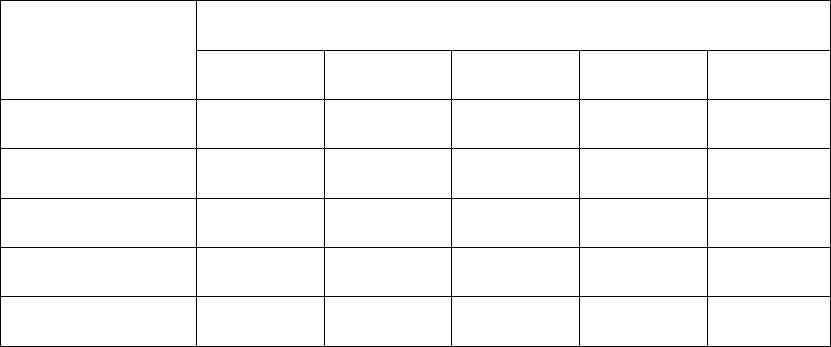
Таблица 3. Доход (прибыль) в день.

Возможные исходы: спрос пирожных в день

Объем

производства

1 2 3 4 5

1 6 6 6 6 6

2 2 12 12 12 12

3 –2 8 18 18 18

4 –6 4 14 24 24

5 –10 0 10 20 30

2.1.1. Правило максимакса – максимизация максимального дохода.

В каждой альтернативе найдем исход с максимальной оценкой (в табл.3

они все находятся в последнем столбце), и выбираем альтернативу,

позволяющую получить самый большой доход. В нашем примере это

соответствует решению производить 5 пирожных. Данный подход

использует азартный карточный игрок (или пан или пропал).

2.1.2. Правило максимина (Вальда) – максимизация минимального

дохода. В каждой альтернативе найдем исход с минимальной оценкой (в

табл.3 они все находятся в первом столбце), и выбираем альтернативу,

позволяющую максимизировать доход в самых худших для нас исходах. В

нашем примере это соответствует решению производить 1 пирожное. Это

очень осторожный подход к принятию решений – стратегия

крайнего

пессимиста.

2.1.3. Правило минимакса (Сэвиджа) – минимизация максимально

возможных потерь. Составим таблицу возможных потерь или упущенной

выгоды. Она составляется из таблицы доходов следующим образом:

для каждого исхода (столбца) находится максимальный доход, затем

вычисляются максимально возможные потери всех альтернатив данного

исхода (из максимального дохода вычитается доход соответствующей

альтернативы).

Таблица 4. Возможные потери

в день.

Возможные исходы: спрос пирожных в день

Объем

производства

1 2 3 4 5

1 0 6 12 18

2 4 0 6 12

3 8 4 0 6

8 4 0 6

12 8 4 0

Для каждой альтернативы находятся максимально возможные потери

(выделены жирным цветом). Затем выбирается та альтернатива, которой

соответствует минимальное значение максимальных потерь. В данном

примере этому правилу подходят альтернативы выпускать три или четыре

пирожных в день.

2.1.4. Правило, основанное на принципе неопределенности Лапласа. В

соответствие с этим принципом предполагается, что все исходы