Gebali F. Analysis Of Computer And Communication Networks
Подождите немного. Документ загружается.

Problems 379
differences. Explain why slotted ALOHA is expected to perform better than
ALOHA.
10.12 Write down the ratio of throughput for slotted ALOHA compared to ALOHA.
Approximate the expression for the limits when a 1 and a ≈ 1.
10.13 Use Equation (10.45) to find the maximum value for the throughput of a
slotted ALOHA network and the value of a at the maximum.
10.14 Using the results of Section A.6 in Appendix A on page 599, prove that the
maximum throughput of the slotted ALOHA network approaches the value
1/easN →∞.
10.15 Assume a slotted ALOHA network that is operating at its optimum condi-
tions. What is the average number of attempts for a frame to be transmitted
under these conditions?
10.16 Assume a slotted ALOHA network where the frame length is a multiple of
some unit of length with an upper limit on the maximum frame size. Draw a
possible transition diagram for such system and write down the correspond-
ing transition matrix.
10.17 Assume a slotted ALOHA network where the propagation delay is bigger
than the frame time T . Draw a possible transition diagram for such system
and write down the corresponding transition matrix.
10.18 Assume there are 25 users in a slotted ALOHA network. What is the trans-
mission request probability a that corresponds to maximum throughput and
what is the value of the maximum throughput?
10.19 Assume there are 25 users in a slotted ALOHA network and the probability
that a user request access is a = 0.06. What is the throughput of the channel
and what is the probability that a user will successfully transmit frame after
three unsuccessful attempts?
10.20 What is the average number of unsuccessful attempts before a user can trans-
mit a frame in the above problem?
10.21 Compare the maximum throughput values for ALOHA and slotted ALOHA
and the level of activity for the sources under these conditions assuming the
same number of users in both systems.
10.22 Assume an ALOHA network and a slotted ALOHA network. Both systems
support N users and each user is active with probability a = 0.02. What is
the optimum value of N for maximum throughput for both systems?
IEEE 802.3 (CSMA/CD, Ethernet)
10.23 Prove that the throughput for the IEEE 802.3 protocol in Section 10.5 ap-
proaches n/(n +1) when under heavy traffic.
10.24 Assume an IEEE 802.3 network where the frame length is not constant. In
that case, the number of time slots required by the transmitted frames could
take between n
min
and n
max
slots.
(a) Draw the resulting state transition diagram.
380 10 Modeling Medium Access Control Protocols
(b) Indicate on the diagram the transition probabilities.
(c) Write down the state transition matrix.
10.25 Assume the backoff parameter f = 1. What will be the expressions for the
IEEE 802.3 protocol
(a) Throughput
(b) Input traffic at maximum throughput
(c) Maximum throughput value
10.26 Assume an IEEE 802.3 network in which a transmitting user could move on
to transmit another frame without turning to the idle state. The probability of
this event happening is c.
(a) Identify the possible states of this Markov chain.
(b) Study the state transition probabilities and write down the state transition
matrix.
10.27 Analyze the IEEE 802.3 for p-persistent CSMA/CD where all collided users
attempt to access the channel with probability p.
10.28 Assume in the 802.3 that a collided station attempts a retransmission for a
limited number of times (assume two only). If it fails after two attempts, it
returns back to being idle. Analyze this situation.
10.29 In our analysis of CSMA/CD, we did not implement the exponential backoff
strategy for collided stations. How could the model we developed here be
modified to include this? Is there an alternative way to analyze this situation?
IEEE 802.11
10.30 Explain what is meant by the following PHY layer terms: frequency-hopping
spread-spectrum (FHSS), direct-sequence spread-spectrum (DSSS) link layer,
orthogonal frequency division multiple access (OFDM).
10.31 Explain what is meant by infrastructure wireless networks.
10.32 Explain what is meant by ad hoc wireless networks.
10.33 Explain what is meant by wireless sensor networks. How do these differ from
ad hoc networks?
10.34 Explain the operation of the distributed coordination function (DCF) and in-
dicate the type of LAN that uses it (infrastructure or ad hoc).
10.35 Explain how DCF reduces the probability of collisions.
10.36 Develop a discrete-time Markov chain model for the IEEE 802.11 user under
the DCF function. Choose a time step value equal to the propagation delay.
10.37 Simulate the performance of the IEEE 802.11 channel for different values of
the number of reservation slots w.
10.38 The analysis of the IEEE 802.11/DCF protocol assumed equally likely
assignment of users to the w reservation slots. Develop a model of the
References 381
channel when the assignment of active users to reservation slots follows a
distribution different from the uniform distribution.
10.39 The analysis of the IEEE 802.11/DCF protocol assumed that the backoff
counters of active users decrement by one when the channel is free. Develop
a model of channel when the backoff counters assume a new random value
each time the channel is busy. Only users that can transmit a frame are the
ones that happen to have a backoff counter value of 0.
10.40 Explain the operation of the point coordination function (PCF) and indicate
the type of LAN that uses it (infrastructure or ad hoc).
10.41 Explain why PCF eliminates collisions.
10.42 Investigate the types of scheduling protocols that could be used in the PCF
portion of the IEEE 802.11 channel.
10.43 Develop a discrete-time Markov chain model for the IEEE 802.11 user under
the PCF function. Choose a time step value equal to the poll period.
10.44 Repeat Example 10.4 for the case when the number of requests per user in-
creases to 100 each second. Comment on your results.
10.45 Assume the IEEE 802.11/PCF protocol that serves 10 customers and the
channel speed is 1 Mbps. Each customer is assumed to issue requests at a
rate of 100 requests/s and the average length of a frame is 5.12 kb. Obtain the
performance of this system.
10.46 Analyze the IEEE 802.11/PCF protocol in which there are two customer
classes. Class 1 has N
1
customers and class 2 has N
2
customers. Users in
class 1 can access the channel when they issue a request, while users in class
2 can only access the channel when none of the users of class 1 has a request.
The system can be modeled as two separate queues for each class but the
transition probabilities in class 2 queue depends on the state of requests of
class 1.
10.47 In the analysis of the IEEE 802.11/PCF protocol, where users had transmit
buffers, it was assumed that requests arriving at a given time step are pro-
cessed in that time step. Develop a new analysis that processes these requests
at the next time step.
References
1. A.S. Tanenbaum, Computer Networks, Prentice Hall PTR, Upper Saddle River, New Jersey,
1996.
2. L. Roberts, “Extension of frame communication technology to a hand held personal terminal”,
NCC, AFIPS, pp. 711–716, 1973.
3. S. Keshav, An Engineering Approach to Computer Networks, Addison-Wesley, Reading,
Massachusetts, 1997.
4. R.M. Metcalfe and D.R. Boggs, “Ethernet: Distributed frame switching for local computer
networks”, Communications of the ACM, vol. 19, pp. 395–404, 1976.
5. F.A. Tobagi, “Analysis of a two-hop centralized frame radio network: Part I — Slotted Aloha”,
IEEE Transactions on Communications, vol. COM-28, pp. 196–207, 1980.
382 10 Modeling Medium Access Control Protocols
6. M.E. Woodward, Communication and Computer Networks, IEEE Computer Society Press,
Los Alamitos, California, 1994.
7. A. Leon-Garcia and I. Widjaja, Communication Networks, McGraw-Hill, New York, 2000.
8. D.B. Jhonson and D.A. Maltz, “Dynamic source routing in Ad Hoc wireless networks”, in
Mobile Computing, T. Imielinski and H. Korth, Eds., Kluwer Academic Publishers, 1996.
9. P. Karn, “MACA - A new channel access method for frame radio”, ARRL/CRRL Amateur
Radio 9th Computer Networking Conference, September,1990.
10. S. Kapp, “802.11a. More bandwidth without the wires”, IEEE Internet Computing,vol.6,
no. 4, pp. 75–79, 2002.
11. J. Weinmiller, H. Woesner, and A. Wolisz, “Analyzing and improving the IEEE 802.11-MAC
protocol for wireless LANs”, Proceedings of the Fourth International Workshop on Model-
ing, Analysis, and Simulation of Computer and Telecommunication Systems (MASCOTS’96),
pp. 200–206, February, 1996.
12. S. Khurana, A. Kahol, S.K.S. Gupta, and P.K. Srimani, “Performance evaluation of distributed
coordination function for IEEE802.11 wireless LAN protocol in presence of mobile and hid-
den terminals”, Proceedings of 7th International Symposium on Modeling, Analysis and Sim-
ulation of Computer and Telecommunication Systems, pp. 40–47, Oct. 1999.
13. J. Liu, D.M. Nicol, L.F. Perrone, and M. Liljenstam, “Towards high performance modeling
of the 802.11 wireless protocol”, Proceedings of the Winter Simulation Conference,vol.9,
pp. 1315–1320, December 2001.

Chapter 11
Modeling Network Traffic
11.1 Introduction
Models that describe and generate telecommunication traffic are important for
several reasons [1]:
Traffic description: Network users might be required to give a traffic description
to the service provider. Based on that, the service provider decides whether
the new connection can be admitted with a guaranteed quality of service and
without violating the quality of service for established connections.
System simulation: Future networks and new equipment could be designed and
the expected network performance checked.
Different models are used to describe different types of traffic. For example, voice
traffic is commonly described using the on–off source or the Markov modulated
Poisson process. Studies suggest that traffic sources such as variable-bit-rate video
and Ethernet traffic are better represented by self-similar traffic models [2–7]. The
important characteristics of a traffic source are its average data rate, burstiness, and
correlation. The average data rate gives an indication of the expected traffic volume
for a given period of time. Burstiness describes the tendency of traffic to occur in
clusters. A traffic burst affects buffer occupancy and leads to network congestion
and data loss. Data burstiness is manifested by the autocorrelation function which
describes the relation between packet arrivals at different times. It was recently dis-
covered that network traffic exhibits long-range dependence, i.e., the autocorrelation
function approaches zero very slowly in comparison with the exponential decay
characterizing short-range-dependent traffic [2–7]. Long-range-dependent traffic
produces a wide range in traffic volume away from the average rate. This great
variation in traffic flow also affects buffer occupancy and network congestion. In
summary, high burstiness or long-term correlation leads to buffer overflow and net-
work congestion. We begin by discussing the different models describing traffic
time arrival statistics.
Simple traffic models are sometimes called point processes since they are ba-
sically counting processes that count the number of packets that arrive in a time
F. Gebali, Analysis of Computer and Communication Networks,
DOI: 10.1007/978-0-387-74437-7
11,
C
Springer Science+Business Media, LLC 2008
383
384 11 Modeling Network Traffic
interval. These point processes sometime give the random sequence representing the
time separations between packets. Several random processes are grouped together to
give more complex traffic patterns. The Internet traffic archive (http://ita.ee.lbl.gov/
index.html) provides data sets for network traffic and some useful software.
The other extreme for traffic modeling is to use fluid flow models. Fluid flow
modeling groups the traffic into flows that are characterized by average and burst
data rates. The object in these models is to investigate traffic at the aggregate level
such as Ethernet traffic or traffic arriving at ingress and egress points of some Inter-
net service provider (ISP). Fluid flow models do not concern themselves with the
details of individual packet arrivals or departures.
The difference between point processes and fluid flow models is similar to the
difference in modeling an electric current in terms of the individual electrons or in
terms of the current equations.
11.2 Flow Traffic Models
Flow traffic or fluid traffic models hide the details of the different traffics flowing
in the network and replace them with flows that have a small set of characterizing
parameters. The resulting models are easily generated, measured, or monitored.
For an end-to-end application, a flow has constant addressing and service re-
quirements [8]. These requirements define a flow specification or flowspec, which
is used for bandwidth planning and service planning. Individual flows, belonging
to single sessions or applications, are combined into composite flows that share the
same path, link, or service requirements. Composite flows, in turn, are combined
into backbone flows when the network achieves a certain level of hierarchy. De-
scribing flows in this fashion makes it easier to combine flow characteristics and to
work with a smaller set of data. For example, a core router might separate incoming
data into individual flows, composite flows, and backbone flows depending on the
quality of service (QoS) required by the users. This results in smaller number of ser-
vice queues and simpler implementation of the scheduling algorithm implemented
in the router. In most networks, the majority of the flows are low-performance
backbone flows; there will also be some composite flows, and there will be few
high-performance individual flows. The high-performance flows will influence the
design of the scheduling algorithm in the switch, size, and number of the queues
required since they usually have demanding delay and/or bandwidth requirements.
The backbone flows will influence the buffer size required since they will usually
constitute the bulk of the traffic and most of the storage within the switch.
11.2.1 Modulated Poisson Processes
In a Markov modulated traffic model, states are introduced where the source changes
its characteristic based on the state it is in. The state of the source could represent its
data rate, its packet length, etc. When the Markov process represents data rate, the
source can be in any of several active states and generates traffic with a rate that is
11.2 Flow Traffic Models 385
determined by the state. This is commonly called Markov modulated Poisson pro-
cess (MMPP). The simplest model is the on–off model, and more complex models
are described in the next section for video traffic.
11.2.2 On–Off Model
A popular model for bursty sources is the on–off model, where the source switches
between an active state, producing packets, and a silent state, where no packets
are produced. In that sense, the on–off model is a two-state MMPP. Traffic from
this type of source is characterized by many variable length bursts of activity, in-
terspersed with variable length periods of inactivity. This model is commonly used
to describe constant bit rate (CBR) traffic in ATM [9, 10]. Figure 11.1 shows the
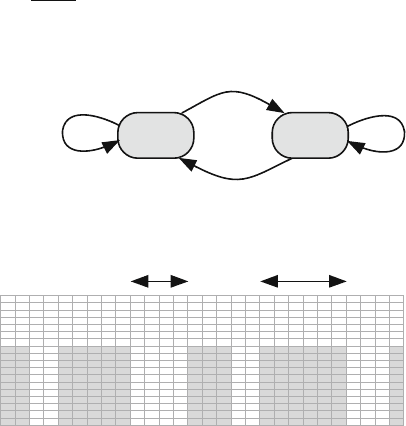
two-state model for the on–off source.
The source stays in the active state with probability a and stays in the silent state
with probability s. When the source is in the active state (called the soujorn time),
the source generates data at a rate λ in units of bits per second or packets per second.
The traffic pattern generated by this source is shown in Fig. 11.2.
The probability that the length of the active period is n time steps is given by the
geometric distribution
A(n) = a
n
(1 −a) n ≥ 1 (11.1)
The average duration of the active period is given by
T
a
=
a
1 −a
time steps (11.2)
Fig. 11.1 An on–off source
model
Silent
State
1-a
1-s
s
a
Active
State
Fig. 11.2 Packet pattern for
an on–off source model
Active
Period
Silent
Period
Time
0
Data rate

386 11 Modeling Network Traffic
Similarly, the probability that the length of the silent period is n time steps is
given by the geometric distribution
S(n) = s
n
(1 −s) i ≥ 1 (11.3)
The average duration of the silent period is given by
T
s
=
s
1 −s
time steps (11.4)
Assume that λ is the data rate when the source is in the active state. In that case,
the average data rate is obtained as
a
=
× T
a
T
a
+ T
s
=
1 + T
s
/T
a
≤ (11.5)
Example 11.1 Assume a 64 kbit/s voice source which is modeled as an on–off
source with an average duration of the active period of T
a
= 0.45 s and average
duration of the silent period is T
s
= 1.5 s. Estimate the source parameters and the
average data rate.
From (11.2), the probability that the source remains in active state is
a =
T
a
1 + T
a
= 0.3103
From (11.4) the probability that the source remains silent is
s =
T
s
1 + T
s
= 0.6
The average data rate is
a
= 14.77 kbps
11.2.3 Markov Modulated Poisson Process
The on–off traffic source model does not describe too well the effect of multiplexing
several data sources. There is only one rate when the source is active while actual
sources display differing data rates when they are active. To handle this situation,
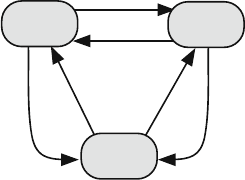
11.3 Continuous-Time Modeling: Poisson Traffic Description 387
Fig. 11.3 A three-state
MMPP source model
State
1
State
3
State
2
p
21
p
12
p
32
p
23
p
13
p
31
more states are added to the MMPP. Figure 11.3 shows a three-state configuration
which is naturally called three-state MMPP.
For an MMPP with N states, we construct an N × N state transition matrix P
whose element p
ij
represents the probability of making a transition from state j to
state i. This choice is consistent with our definition for the transition matrix of a
Markov chain. Needless to say, this matrix is a column stochastic matrix.
When the source is in state i,1≤ i ≤ N, the packets are produced at a rate
i
.
When the number of states is N = 2, we have a switched Poisson process (SPP)
[10]. When N = 2 and
1
= 0, we have an interrupted Poisson process (IPP),
which is also the on–off model that was discussed above.
11.2.4 Autoregressive Models
Autoregressive models produce traffic with short-range dependence where the au-
tocorrelation function decays exponentially. An autoregressive model of order N ,
denoted AR(N), is described by
X
(
n
)
=
N
k=1
a
i
X
(
n − k
)
+
(
n
)
(11.6)
where X
(
n
)
is a random variable indicating the traffic rate at that time;
(
n
)
is a
random variable having a small range to fit experimental data. The above formula
gives a simple method for generating the next random number, given the previous
set of N random numbers which is computationally appealing.
Alternative forms of the above expression using moving average (MA) and au-
toregressive moving average (ARMA) expressions were also proposed [11].
11.3 Continuous-Time Modeling: Poisson Traffic Description
Poisson traffic description is a model often used by many researchers due to the
simplicity of the model. A characteristic of traffic is the lull period in which no
packets arrive. We can think of the interarrival time between two successive packets

388 11 Modeling Network Traffic
as a random variable T . This r.v. is continuous for Poisson traffic. The attractive
feature of Poisson traffic is that the sum of several independent Poisson processes
results in a new Poisson process whose rate is the sum of the component rates [12].
Poisson traffic accurately describes user-initiated TELNET and FTP connections
[4]. To study the random variable T , we need to study the probability p(0) that no
packets arrive in the period t. Let us start by assuming Poisson traffic with proba-
bility p(k) that k packets arrive in a time period t which is given by
p(k) =
(
a
t)
k
k!
e
−
a
t
(11.7)
where
a
(packets/s) is the average packet arrival rate. Note that this expression for
probability is valid for all values of 0 ≤ k < ∞. Of course, we do not expect an
infinite number of packets to arrive in a time interval t, but this is the expression
and that is what it predicts. Note that Poisson distribution really talks about num-
bers. It specifies the probability of getting a number of packets k in a given time
period t.
For the interarrival time, we ask a different sort of question: what is the probabil-
ity that the time separation between adjacent packets is t? To derive an expression
for the pdf distribution for the interarrival time, we need to find the probability that
no packets arrive in period t. The probability that no packets arrive in a time period
t is obtained by substituting k = 0 in (11.7) to obtain
p(0) = e
−
a
t
(11.8)
This probability is equivalent to the event A : T > t, and we can write
p(A : T > t) = p(0)
= e
−
a
t
(11.9)
The event A is basically the event that no packets arrived for a time period t.
What happens after this time period is not specified. A packet might arrive or no
packets arrive.
In order to find the pdf associated with the interarrival time, we need to define
event B which is complementary to A as follows:
B : T ≤ t
and the probability associated with event B is
p(B : T ≤ t) = 1 − p(A)
= 1 −e
−
a
t
(11.10)
