Gebali F. Analysis Of Computer And Communication Networks
Подождите немного. Документ загружается.

268 7 Queuing Analysis
cannot be served until the next time step. What will be the expression for the
state matrix? Compare your result to (7.94).
7.31 Consider an M/M
m
/1/B queue with arrival probability a = 0.5, departure
probability c = 0.2, m = 2, and maximum queue size B = 5. The queue
is not stable since the average number of arrivals is larger than the average
number of departures.
(a) Construct the transition matrix P.
(b) Find the values of the equilibrium distribution vector.
(c) Calculate the queue performance.
7.32 In the analysis of the M/M
m
/1 queue, it was assumed that when a packet
arrives, it can be serviced at the same time step. Suppose the arriving packet
is serviced the next time step. Draw the state transition diagram and at write
down the corresponding transition matrix. Derive the main performance equa-
tions of such a queue.
References
1. F. Elguibaly, “Analysis and design of arbitration protocols”, IEEE Transactions on Computers,
vol. 38, No. 2, pp. 1168–1175, 1989.
2. D.G. Kendall, “Stochastic processes occurring in the theory of queues and their analy-
sis by means of the embedded Markov chain”, Annals of Mathematical Statistics, vol. 24,
pp. 338–354, 1953.
3. M. E. Woodward, Communication and Computer Networks, IEEE Computer Society Press, Los
Alamitos, CA, 1994.
4. I. Peterson, Fatal Defect: Chasing Killer Computer Bugs, Random House, New York, 1995.
5. W.J. Stewart, Introduction to Numerical Solutions of Markov Chains, Princeton University
Press, Princeton, New Jersey, 1994.
6. J. Billington, M. Diaz and G. Rozenberg (eds.), Application of Petri Nets to Communication
Networks: Advances in Petri Nets, Springer, New York, 1999.
7. K. Jensen, Coloured Petri Nets: Basic Concepts, Analysis Methods and Practical Use, Springer-
Verlag, New York, 1997.

Chapter 8
Modeling Traffic Flow Control Protocols
8.1 Introduction
In this chapter, we illustrate how to develop queuing models for three protocols of
traffic management:
1. The leaky bucket algorithm
2. The token bucket algorithm
3. Virtual scheduling algorithm (VS)
Modeling a protocol or a system is just like designing a digital system, or any
system for that matter. There are many ways to model a protocol based on the as-
sumptions that one makes. My motivation here is simplicity and not taking a guided
tour through the maze of protocol modeling. My recommendation to the reader is
to read the discussion on each protocol and then lay down the outline of a model
that describes the protocol. The model or models developed here should then be
compared with the one attempted by the reader.
8.2 The Leaky Bucket Algorithm
Computer traffic is seldom uniform and is characterized by periods of burstiness.
Traffic bursts tax the network resources such as switch buffers and lead to network
congestion and data loss. Because it is impossible for the network to accept only
uniform traffic, mechanisms have been proposed to regulate or smooth out these
bursts.
Thus traffic shaping, also known as traffic policing, aims at regulating the aver-
age rate of traffic flow even in the presence of occasional bursts [1]. This helps to
manage the congestion problem at the switches.
When a user accesses the network, the important parameter to describe the traffic
is the average data rate (λ
a
). This is estimated by observing the number of packets
(N) sent over a long time interval t and finding the average data rate as λ
a
= N/t.
This rate is compared to a maximum rate (λ
b
) that is specified by the leaky bucket
algorithm. As long as λ
a
<λ
b
, the user is classified as conforming, and data is
F. Gebali, Analysis of Computer and Communication Networks,
DOI: 10.1007/978-0-387-74437-7
8,
C
Springer Science+Business Media, LLC 2008
269
270 8 Modeling Traffic Flow Control Protocols
accepted. Users that obey this traffic contract are termed conforming users, while
users that violate this contract are termed violating or nonconforming users.Traffic
policing to ensure that each user is conforming is done at the points where users
access the network (ingress points).
Leaky bucket is a rate-based algorithm for controlling the maximum rate of traf-
fic arriving from a source. If the input data rate is less than the maximum rate spec-
ified by the algorithm, leaky bucket accepts the data. If the input data rate exceeds
the maximum rate, leaky bucket passes the data at the maximum rate and excess
data is buffered. If the buffer is full, then excess data is discarded. In our modeling
of the leaky bucket algorithm, we are interested only in the state of the data buffer
since the state of that buffer dictates the actions to be done on the incoming traffic.
Our aim then is to simply model the buffer state so that we are able to predict the
performance of the algorithm.
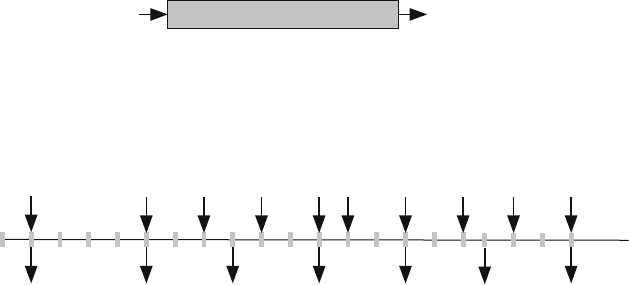
Figure 8.1(a) shows the leaky bucket buffer. The buffer accepts incoming data
and releases the stored packets at a data rate that does not exceed λ
b
. Depending on
the data arrival rate λ
a
and the state of occupancy of the packet buffer, the following
scenarios could take place.
1. λ
a
<λ
b
: Data arrive at a rate (λ
a
) lower than the maximum rate (λ
b
) specified by
the leaky bucket algorithm. In that case, data will be accepted as shown by the
arrival of packets 1 and 2 in Fig. 8.1(b). The long time interarrival time between
packets 1 and 2 indicate a low data arrival rate. We assumed in the figure that the
maximum departure rate λ
b
is equivalent to three time steps between packets.
As soon as these packets arrive, they are passed through by the leaky bucket
algorithm.
Variable rate
input traffic
Output traffic with
fixed maximum rate
Packet buffer
Output traffic with maximum rate
time
1235674
123 54
(a)
(b)
Input traffic with variable rate
6
8 9 10
7
Fig. 8.1 The leaky bucket algorithm smoothes input variable rate traffic by buffering it and regu-
lating the maximum buffer output traffic rate: (a) Packet buffer; (b) Packet arrival and departure

8.2 The Leaky Bucket Algorithm 271
2. λ
a
>λ
b
: Data arrive at a rate higher than λ
b
, and the data buffer is not full. In
that case, data will be buffered so that it can be issued at the maximum rate λ
b
.
This is shown by the arrival of packets 3, 4, and 5 in Fig. 8.1(b). Note that packets
3, 4, and 5 arrive close together in time at the input indicating a high-input data
rate. The interarrival time is 2 time steps, which indicates higher data rate than λ
b
which is equivalent to two time steps. At the output, the spacing between these
packets is equivalent to data transmitted at the rate λ
b
.
3. λ
a
>λ
b
: Data arrive at a rate higher than λ
b
, and the data buffer is full. In that
case, data will be discarded or labeled as nonconforming. This is shown by, ar-
rival of packets 6 and 7 in Fig. 8.1(b).
Figure 8.2 shows the variation of output data rate in relation to the input data rate.
Grey areas indicate input data rate and solid black lines indicate maximum data rate
λ
b
. Output data rate does not exceed λ
b
, and any excess input traffic is buffered or
lost. The figure shows two occasions when the input data rate exceeds λ
b
. When this
situation happens, excess data are buffered and then released when the output data
rate becomes low again.
8.2.1 Modeling the Leaky Bucket Algorithm
In this section, we perform Markov chain analysis of the leaky bucket algorithm.
The states of the Markov chain represent the number of packets stored in the leaky
bucket buffer.
Packets arrive at the input of the buffer at a rate λ
in
, which varies with time
because of the burstiness of the source. To model the source burstiness in a simple
manner, we assume that the data source has the following parameters:
λ
a
average data rate of source
σ source burst rate when it is nonconforming
λ
a
and σ typically satisfy the relations
λ
a
<λ
b
(8.1)
σ>λ
b
(8.2)
Time0
Maximum output rate
Data rate
Fig. 8.2 Control of data rate by the leaky bucket algorithm. Data rate at the input is indicated by
the grey areas, and data rate at the output is indicated by the black lines

272 8 Modeling Traffic Flow Control Protocols
where λ
b
is the maximum data departure rate as determined by the leaky bucket
algorithm.
On the other hand, packets leave the buffer with an output rate λ
out
given by
λ
out
=
min
(
λ
in
,λ
b
)
when packet buffer is empty
λ
b
when packet buffer is not empty
(8.3)
Notice that the output data rate is governed by the state of the data buffer and not
by the input data rate.
The leaky bucket algorithm can be modeled using two different types of queues
depending on our choice of the time step. These two approaches are explained in
the following two sections.
8.2.2 Single Arrival/Single Departure Model (M /M /1 /B)
In this approach to modeling the leaky bucket algorithm, we take the time step equal
to the inverse of the maximum data rate on the line.
T =
1
λ
l
(8.4)
where the time step value is measured in units of seconds, and λ
l
is the maximum
input line rate (in units of packets/second) such that
λ
b
<λ
l
The above inequality is true since the line is shared by many users. The time T
is the time between packet arrivals at the maximum allowable rate on the input line.
When λ
l
is specified in units of bits per second (bps), T is obtained as
T =
A
λ
l
(8.5)
where A is the average packet length.
Figure 8.3 shows the events of packet arrival and departure and also the time step
value as indicated by the spacing between the grey tick marks.
At a given time step, a maximum of one packet could arrive at or leave the buffer.
The packet arrival probability (a) is given by studying the number of arriving pack-
ets in a time t. The average number of packets arriving in this time frame is
N(in) = λ
a
t (8.6)

8.2 The Leaky Bucket Algorithm 273
Variable rate input traffic
Output traffic with maximum rate
time
time step
1 2345
12345
67
Fig. 8.3 The leaky bucket algorithm where the time step is chosen equal to the inverse of the
maximum line rate
But during this time period, we have N time steps with N = t/T . The average
number of arriving packets is estimated also using the binomial distribution as
N(in) = aN= a
t
T
(8.7)
From the above two equations, we get
a = λ
a
T =
λ
a
λ
l
(8.8)
Of course, when the source is conforming, the departure probability is c = 1.
Using a similar argument, the minimum packet departure probability (c)isgiveby
c =
λ
out
λ
l
(8.9)
Therefore, we have a single-input, single-output data buffer whose size is as-
sumed B. The queue, we are studying becomes M/M/1/B queue, and the transition
matrix is (B + 1) ×(B + 1) and is given by
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
f
0
bc 00··· 000 0
ad f bc 0 ··· 000 0
0 ad f bc ··· 000 0
00ad f ··· 000 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0000··· fbc00
0000··· ad f bc 0
0000··· 0 ad f bc
0000··· 00ad 1 −bc
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(8.10)
where b = 1 −a, d = 1 −c, f
0
= 1 −ad, and f = 1 −ad − bc.
274 8 Modeling Traffic Flow Control Protocols
8.2.3 Leaky Bucket Performance (M /M /1/B Case)
Having obtained the transition matrix, we are able to calculate the performance of
the leaky bucket protocol.
The throughput of the leaky bucket algorithm when the M/M/1/B model is used
is given from Section 7.6 by
Th = c
(
1 −bs
0
)
(8.11)
The throughput is measured in units of packets/time step. The throughput in units
of packets/second is expressed as
Th
=
Th
T
= Th ×
λ
l
A
(8.12)
whereweassumedλ
l
was given in units of bits/second.
The average number of lost or tagged packets per time step is obtained using the
results of the M/M/1/B queue
N
a
(lost) = s
B
ad (8.13)
The lost traffic is measured in units of packets/time step. And the number of
packets lost per second is
N
a
(lost) =
N
a
(lost)
T
= N
a
(lost) ×
λ
l
A
(8.14)
where we assumed λ
l
was given in units of bits/second. The packet loss probability
is given by
L =
N
a
(lost)
N
a
(in)
=
s
B
ad
λ
a
(8.15)
The average queue size is given by
Q
a
=
B
i =0
is
i
(8.16)
where s
i
is the probability that the data buffer has i packets.
Using Little’s result, the average wait time in the buffer is
W =
Q
a
Th
(8.17)

8.2 The Leaky Bucket Algorithm 275
The wait time is measured in units of time steps. The wait time in units of seconds
is given by
W
=
Q
a
Th
(8.18)
Example 8.1 A leaky bucket traffic shaper has the following parameters.
λ
a
= 1 Mbps σ = 4 Mbps
λ
b
= 1.5 Mbps λ
l
= 50 Mbps
A = 400 bits B = 5 packets
Derive the performance of this protocol using the M/M/1/B modeling approach.
The arrival probability is
a =
λ
a
λ
l
= 0.02
The minimum departure probability is
c =
λ
b
λ
l
= 0.03
We see that under the assumed traffic conditions the arrival probability is larger
than the departure probability and we expect the packet buffer to be filled.
The transition matrix will be
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.9399 0.0281 0000
0.0601 0.9117 0.0281 0 0 0
00.0601 0.9117 0.0281 0 0
000.0601 0.9117 0.0281 0
0000.0601 0.9117 0.0281
000 0.0601 0.9719
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
The equilibrium distribution vector is
s =
0.0121 0.0258 0.0551 0.1177 0.2516 0.5377
t
Since s
5
= 0.5377, we conclude that 53.77% of the time the packet data buffer
is full. The other performance parameters are

276 8 Modeling Traffic Flow Control Protocols
Th = 0.0297 packets/time step
Th
=3.7076 × 10
3
packets/s
N
a
(lost) = 0.0323 packets/time step
N
a
(lost) = 4.0424 ×10
3
packets/s
L =1.0432 ×10
−8
Q
a
= 4.1843 packets
W = 141.0713 times steps
W
= 94.048 s
We note that the leaky bucket is tagging or dropping 76.02% of the incoming
packets.
8.2.4 Multiple Arrival/Single Departure Model (M
m
/M /1/B)
In this approach to modeling the leaky bucket algorithm, we take the time step equal
to the inverse of the maximum data rate as dictated by the leaky bucket algorithm
for that particular source.
T =
1
λ
b
(8.19)
where the time step is measured in units of seconds and the leaky bucket rate λ
b
is
in units of packets/second. Usually, λ
b
is specified in units of bits/second. In that
case, T is obtained as
T =
A
λ
b
(8.20)
where A is the average packet length.
Figure 8.4 shows the events of packet arrival and departure and also the time step
value as indicated by the spacing between the successive output packets.
Variable rate input traffic
Output traffic with maximum rate
time
time step
12345
12345
67
Fig. 8.4 Events of packet arrival and departure for the leaky bucket algorithm. The time step value
is equal to the time between two adjacent output packets

8.2 The Leaky Bucket Algorithm 277
At a given time step, one or more packets could arrive at the buffer and only
one packet can leave if the buffer is not empty. Therefore, we have an M
m
/M/1/B
queue to describe the state of the packet buffer.
The average data rate of the source as seen by the leaky bucket algorithm is given
by λ
a
. The maximum number of packets that could arrive at the queue input in one
time step is determined by the maximum burst rate σ
N =σ × T =
$
σ
λ
b
%
(8.21)
where x the is ceiling function which produces the smallest integer that is larger
than or equal to x.
The probability of k packets arriving in one time step is given by
a
k
=
N
k
a
k
b
N−k
k = 0, 1, 2, ..., N (8.22)
where a is the probability that a packet arrives and b = 1 −a.
The average number of packets arriving in one time step is estimated as
N
a
(in) = λ
a
T (8.23)
The average input packets is estimated also using the binomial distribution as
N
a
(in) = aN= a σ T (8.24)
From the above two equations, we get
a =
λ
a
T
σ T
≤
λ
a
σ
(8.25)
Because of our choice for the time step size, the queue size can only decrease by
one at most at any instant with probability c = 1. Assuming the packet buffer size
is B, the transition matrix will be (B + 1) ×(B + 1) and will be slightly modified
from the form given by (7.63) on page 241:
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
xa
0
000··· 0
a
2
a
1
a
0
00··· 0
a
3
a
2
a
1
a
0
0 ··· 0
a
4
a
3
a
2
a
1
a
0
··· 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0
a
B
a
B−1
a
B−2
a
B−3
a
B−4
··· a
0
z
B
z
B−1
z
B−2
z
B−3
z
B−4
··· z
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(8.26)
