Gebali F. Analysis Of Computer And Communication Networks
Подождите немного. Документ загружается.

248 7 Queuing Analysis
7.8 M/M
m
/1/B Queue
In an M/M
m
/1 queue at any time step, at most one customer could arrive and at
most m customers could leave. We shall encounter this type of queue when we
study network switches where first-in-first-out (FIFO) queues exist at each input
port. For each queue, one packet arrives at the input line to the storage buffer, but a
maximum of m packets can leave the queue destined to the different switch outputs.
Therefore, the queue size can increase by one, but can decrease by more than one.
The probability that a packet arrives is a and b = 1 − a is the probability that a
packet does not arrive at a time step. Define c
i, j
as the probability that j customers
leave the queue when there are i customers in the queue.
c
i, j
=
i
j
c
j
d
i−j
(7.93)
where c is the probability that a packet departs and d = 1 − c. The state transition
matrix is an upper (B + 1) × (B + 1) Hessenberg matrix in which all the elements
of subdiagonals 2, 3, ... are zero—i.e., p
ij
= 0fori > j + 1. The matrix has only
m superdiagonals. If we assume an arriving packet is served at the same time step,
then the transition matrix for the case when B = 6 and m = 3 will have the form
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
q
0
r
1
s
2
t
3
000
p
0
q
1
r
2
s
3
t
4
00
0 p
1
q
2
r
3
s
4
t
5
0
00p
2
q
3
r
4
s
5
y
000p
3
q
4
r
5
x
2
0000p
4
q
5
x
1
00000p
5
x
0
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(7.94)
where the matrix elements are given by the general expressions
p
i
= ac
i+1,0
(7.95)
q
i
= ac
i+1,1
+bc
i,0
(7.96)
r
i
= ac
i+1,2
+bc
i,1
(7.97)
s
i
= a
i+1
j=m
c
i+1, j
+bc
i,2
(7.98)
t
i
= b
i
j=m
c
i, j
(7.99)
x
i
= c
6,i
(7.100)
y =
B
j=m
c
B, j
(7.101)

7.8 M/M
m
/1/B Queue 249
The condition for the stability of the queue is when average traffic at the queue
input is smaller than the average traffic at the queue output:
a < mc (7.102)
7.8.1 M/M
m
/1/B Queue Performance
The average input traffic for the M/M
m
/1/B queue is obtained simply as
N
a
(in) = a (7.103)
Traffic is lost in the M/M
m
/1/B queue when it becomes full and a packet
arrives while no packets leave. The average lost traffic N
a
(lost) is expressed
simply as
N
a
(lost) = as
B
c
B,0
(7.104)
The packet loss probability L is the ratio of lost traffic relative to the input
traffic:
L =
N
a
(lost)
N
a
(in)
= s
B
c
B,0
(7.105)
The throughput of the queue is obtained using the traffic conservation principle:
Th = N
a
(in) − N
a
(lost)
= a
(
1 −s
B
)
(7.106)
The efficiency of the M/M
m
/1/B queue is given by
η = 1 − L
= 1 −s
B
c
B,0
(7.107)
The average queue size is given by the equation
Q
a
=
B
i=0
is
i
(7.108)
We can invoke Little’s result to estimate the wait time, which is the average num-
ber of time steps a packet spends in the queue before it is routed:
Q
a
= W ×Th (7.109)

250 7 Queuing Analysis
where W is the average number of time steps that a packet spends in the queue.
Thus, W is give by
W =
Q
a
Th
(7.110)
The wait time is measured in units of time steps. The wait time in units of seconds
is given by the unnormalized version of Little’s result.
W
=
Q
a
Th
(7.111)
Example 7.9 Consider the M/M
m
/1/B queue with the following parameters
a = 0.1, c = 0.07, m = 2, and B = 5. Check its stability condition and find
the equilibrium distribution vector and the queue performance.
Using (7.94), the transition matrix is
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎣
0.9070 0.0635 0.0044 0 0 0
0.0930 0.8500 0.1186 0.0126 0 0
00.0865 0.7966 0.1661 0.0241 0
000.0804 0.7464 0.2069 0.0425
0000.0748 0.6994 0.2618
00000.0696 0.6957
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎦
The transition matrix has two superdiagonals because m = 2.
The steady-state distribution vector is the eigenvector of P that corresponds to
unity eigenvalue. We have
s =
0.2561 0.3584 0.2414 0.1043 0
.0324 0.0074
t
We see that the most probable state for the queue is state s
1
which occurs with
probability 35.8%.
The queue performance is as follows:
N
a
(lost) = 6.4058 ×10
−4
packets/time step
Th = 0.0994 packets/time step
L = 0.0064 ×10
−2
η = 0.9936
Q
a
= 1.3205 packets
W = 13.2906 time steps
Example 7.10 Find the performance of the queue in the previous example when the
queue size becomes B = 10.
7.8 M/M
m
/1/B Queue 251
The queue performance is as follows:
N
a
(lost) = 2.6263 ×10
−8
packets/time step
Th = 0.1 packets/time step
L = 2.6263 ×10
−7
η = 1
Q
a
= 1.3286 packets
W = 13.2862 time steps
We see that increasing the queue size exponentially decreases the loss probability.
The throughput is not changed by much.
Example 7.11 Plot the M/M
m
/1/B performance when m = 2 and the input traffic
varies between 0 ≤ a ≤ 1forB = 5 and c = 0.05.
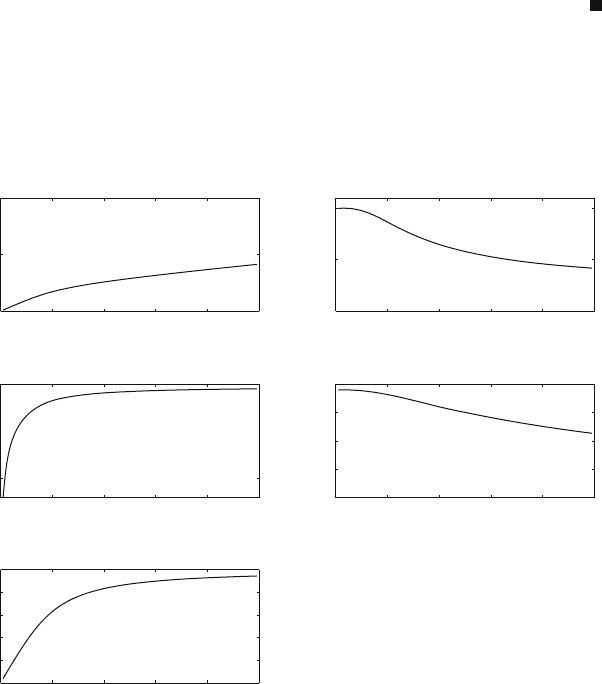
Figure 7.7 shows the throughput, efficiency, loss probability, and delay to plot
these quantities versus input traffic.
0 0.2 0.4 0.6 0.8 1
0
0.5
1
0 0.2 0.4 0.6 0.8 1
0 0.2 0.4 0.6 0.8 1
0 0.2 0.4 0.6 0.8 1
0 0.2 0.4 0.6 0.8 1
0
0.5
1
Input traffic
Throughput
Input traffic
Efficiency
10
−5
10
0
Input traffic
Loss probability
0
5
10
15
20
Input traffic
Delay
0
1
2
3
4
5
Input traffic
Queue Size
Fig. 7.7 M/M
m
/1/B throughput, efficiency, loss probability and delay versus input traffic when
m = 2, B = 5, and c = 0.05

252 7 Queuing Analysis
The important things to note from this example are as follows:
1. The throughput of the queue increases with increasing input traffic but shows
slight decrease when the input traffic approaches the value mc.
2. The efficiency of the queue is very close to 100% until the input traffic ap-
proaches the maximum output traffic mc.
3. Packet loss probability is always present but starts to increase when the input
traffic approaches the value mc.
4. Packet decreases when the input traffic approaches the value mc. This is due to
the queue size becoming constant while the throughput keeps increasing.
7.8.2 Performance Bounds on M/M
m
/1/B Queue
The previous examples help us get some rough estimates for the performance
bounds of the M/M/
m
1/B queue.
Under full load conditions, the M/M
m
/1/B becomes full and we can assume
a → 1 (7.112)
b → 0 (7.113)
s
0
→ 0 (7.114)
s
B
→ 1 (7.115)
Q
a
→ B (7.116)
The maximum lost traffic is given from (7.104) by
N
a
(lost)
max
= c
B,0
= (1 −c)
m
≤ d
m
(7.117)
where n = min(B, m). The reason for the inequality sign is that s
B
seldom
approaches 1.
The maximum packet loss probability is given from (7.105) by
L(max) = c
B,0
= (1 −c)
n
≤ d
n
(7.118)
The maximum throughput is given from (7.106) by
Th(max) = 1 −c
B,0
≥ 1 −(1 −c)
m
= 1 −d
m
(7.119)
7.9 The D/M/1/B Queue 253
The minimum efficiency of the M/M
m
/1/B queue is given from (7.107) by
η(min) ≥ 1 −d
m
(7.120)
The maximum delay is given by the approximate formula
W(max) ≤
B
Th(max)
≤
B
1 −d
m
≤
B
1 −d
m
(7.121)
7.8.3 Alternative Solution Method
When B is large, it is better to use numerical techniques such as forward- or back-
ward substitution using Givens rotations.
At steady state, we can write
Ps= s (7.122)
We can use the technique explained in Section 4.10 on page 140 to construct a
system of linear equations that can be solved using any of the specialized software
designed to solve large systems of linear equations.
7.9 The D/M/1/B Queue
In the D/M/1/B queue, packets arrive at a fixed rate but leave the queue in a ran-
dom fashion. Let us assume that the time step is chosen such that exactly one packet
arrives at the nth time step. Assume also that c is the probability that a packet leaves
the queue during one time step. We also assume that at most one packet leaves
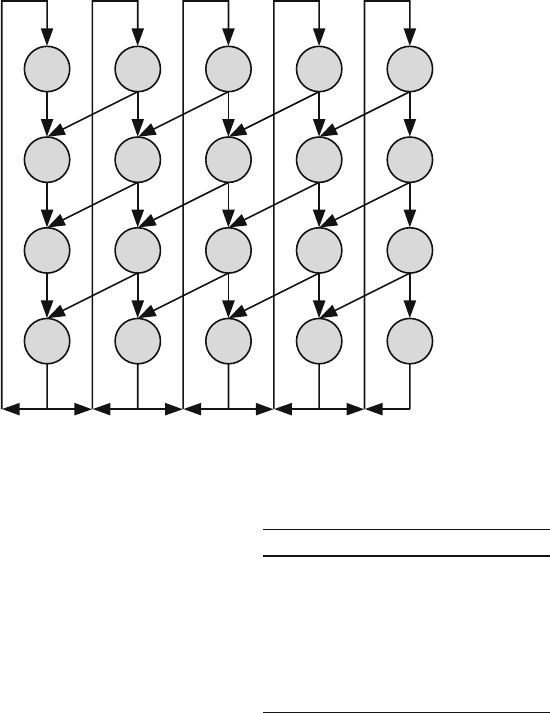
the queue in one time step. d = 1 − c has the usual meaning. Figure 7.8 shows
the state transition diagram for such queue for the case when n = 4 and B = 4
also. The number of rows correspond to the number of time steps between packet
arrivals. The last row corresponds to the states when a packet arrives. The number of
columns corresponds to the size of the queue such that each column corresponds to a
particular state of queue occupancy. For example, the leftmost column corresponds
to the case when the queue is empty. The rightmost column corresponds to the case
when the queue is full. The state of occupancy of the queue is indicated in Table 7.1.
In that case, we know that a packet arrives when the queue is in one of the bottom
states s
3,0
, s
3,1
, s
3,2
, s
3,3
,ors
3,4
.
254 7 Queuing Analysis
s
0,0
s
0,0
s
1,0
s
2,0
s
3,0
s
0,1
s
1,1
s
2,1
s
3,1
s
0,2
s
1,2
s
2,2
s
3,2
s
0,3
s
1,3
s
2,3
s
3,3
s
0,4
s
1,4
s
2,4
s
3,4
cdcdcdcd
1
1
1
1
c
d
c
d
c
d
c
d
c
d
c
d
c
d
c
d
c
d
c
d
c
d
c
d
Fig. 7.8 State transition diagram for the discrete-time D/M/1/B queue
Table 7.1 Relation of the
queue states and the
D/M/1/B queue occupancy
States Queue occupancy
s
0,0
–s
3,0
Queue empty
s
0,1
–s
3,1
One customer in queue
s
0,2
–s
3,2
Two customers in queue
.
.
.
.
.
.
s
0, j
–s
3, j
j customers in queue
.
.
.
.
.
.
The state vector s can be grouped into B subvectors
s =
s
0
s
1
···s
B
t
(7.123)
where the subvector s
j
correspond to the jth column in Fig. 7.8 and is given by
s
j
=
s
0, j
s
1, j
···s
n−1, j
t
(7.124)
which corresponds to the case when there are j customers in the queue. The
state transition matrix P corresponding to the state vector s will be of dimension
n(B +1) ×n(B + 1). We describe the transition matrix P as a composite matrix of
size (B + 1) ×(B + 1) as follows:
7.9 The D/M/1/B Queue 255
P =
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
AC0··· 000
BDC··· 000
0BD··· 000
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
000··· DC0
000··· BDC
000··· 0BE
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
(7.125)
where all the matrices A, B, C, D, and E are of dimension n×n. For the case n = 4,
we can write
A =
⎡
⎢
⎢
⎣
000c
1000
0100
0010
⎤
⎥
⎥
⎦
, B =
⎡
⎢
⎢
⎣
000d
0000
0000
0000
⎤
⎥
⎥
⎦
, C =
⎡
⎢
⎢
⎣
0000
c 000
0 c 00
00c 0
⎤
⎥
⎥
⎦
D =
⎡
⎢
⎢
⎣
000c
d 000
0 d 00
00d 0
⎤
⎥
⎥
⎦
, E =
⎡
⎢
⎢
⎣
0001
d 000
0 d 00
00d 0
⎤
⎥
⎥
⎦
Having found the state transition matrix, we are now able to find the steady-
state value for the distribution vector of the D/M/1/B queue. At steady state, the
distribution vector s is derived from the two equations
Ps= s (7.126)
1s= 1 (7.127)
where 1 is a row vector whose components are all 1s.
We can find the vector s by iterations as follows. We start by assuming a value
for element s
0,0
= 1. As a consequence, all the elements of the vector s
0
can be
found as follows
s
1,0
= s
0,0
= 1 (7.128)
s
2,0
= s
1,0
= 1 (7.129)
s
3,0
= s
2,0
= 1 (7.130)
.
.
.
Thus, we know that s
0
is assumed to be a vector whose components are all 1s. To
find s
1
we use the equation
s
0
= As
0
+Cs
1
(7.131)

256 7 Queuing Analysis
or
s
1
= C
−1
(I −A)s
0
(7.132)
Since we have an initial assumed value for s
0
, we now know s
1
. In general, we
can write the iterative expressions
s
i
= C
−1
(I −A)s
i−1
1 ≤ i ≤ B (7.133)
Having found all the vectors s
i
, we obtain the normalized distribution vector s
as
s
= s
!
n−1
i=0
B
j=0
s
i, j
(7.134)
7.9.1 Performance of the D/M/1/B Queue
The average input traffic N
a
(in) is needed to estimate the efficiency of the queue and
queue delay. Since we get one packet every n time steps, N
a
(in) is given by
N
a
(in) =
1
n
(7.135)
The throughput of the queue is given by
Th = cs
n−1,0
+c
n−1
i=0
B
j=1
s
i, j
= c
"
1 −
n−2
i=0
s
i,0
#
(7.136)
The efficiency of the D/M/1/B queue is given by
η =
Th
N
a
(in)
= cn
"
1 −
n−2
i=0
s
i,0
#
(7.137)
Packets are lost in the D/M/1B queue when the queue is full and a packet arrives
but does not leave. The average lost traffic is given by
N
a
(lost) = ds
n−1,B
(7.138)
7.10 The M/D/1/B Queue 257
The packet loss probability L is given by
L =
N
a
(lost)
N
a
(in)
= dns
n−1,B
(7.139)
The average queue size is given by
Q
a
=
n−1
i=0
B
j=0
is
i, j
(7.140)
7.10 The M/D/1/B Queue
In the M/D/1/B queue, packets arrive in a random fashion but leave the queue at a
fixed rate. Let us assume that the time step is chosen such that a packet leaves at the
nth time step. Assume also that a is the probability that it arrives at queue during one
time step. b = 1 −a has the usual meaning. We also assume that at most one packet
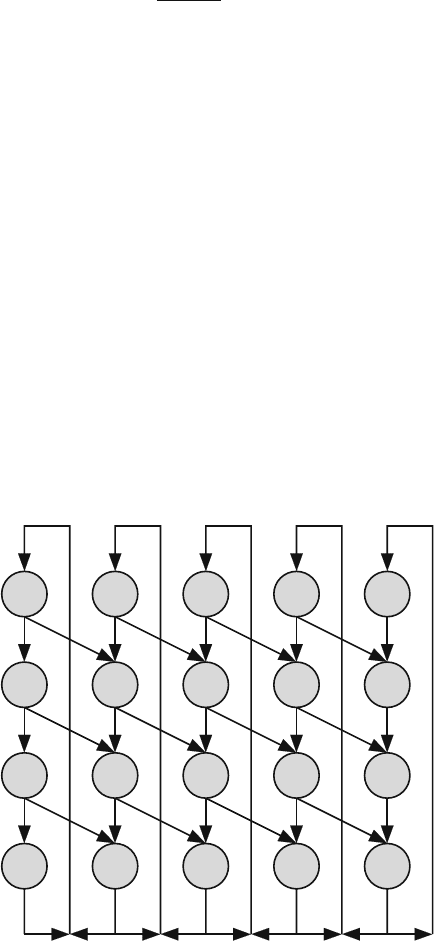
arrives in the queue in one time step. Figure 7.9 shows the state transition diagram
for such queue for the case when n = 4 and B = 4 also. The number of rows
corresponds to the number of time steps between packet departures. The last row
corresponds to the states when a packet leaves. The number of columns corresponds
to the size of the queue such that each column corresponds to a particular state of
queue occupancy. For example, the leftmost column corresponds to the case when
the queue is empty. The rightmost column corresponds to the case when the queue
s
0,0
s
0,0
s
1,0
s
2,0
s
3,0
s
0,1
s
1,1
s
2,1
s
3,1
s
0,2
s
1,2
s
2,2
s
3,2
s
0,3
s
1,3
s
2,3
s
3,3
s
0,4
s
1,4
s
2,4
s
3,4
ab
1
1
1
1
a
b
a
b
a
b
ababab
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
a
b
Fig. 7.9 State transition diagram for the discrete-time M/D/1/B queue
