Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.

91
Согласно (2.112), решение сопряженной системы (2.111) в общем
случае имеет вид
1
)(
1
)( ψetψ
ttA
T
−−
=
, где
1
ψ
– значение решения
)(t
ψ
при
1
tt =
. Положим
∗
=tt
1
, а
T
Сψ =
1
. Тогда
TttA
Cetψ
T
)(
)(
∗
−−
=
.
Транспонируем это выражение, заменим
t
на
τ
, найдем отсюда С и
подставим в равенство (2.134). В результате получим
∫
τττ=
+ht
t
T
dBgψtI
)()()(
.
Таким образом, формулу (2.133) можно записать следующим образом
∫
τττ+=+
+ht
t
ThA
dBgψtxCehty
0
0
)()()()(
00
. (2.135)
Подчеркнем, что в формуле (2.135)
)(tψ
это решение сопряженной
системы (2.111), равное
T
С
при
httt +==
∗
0
, а величина
h
– конечный
интервал интегрирования.
Принцип суперпозиции. Одним из важнейших свойств линейных
динамических систем является то, что они удовлетворяют принципу су-
перпозиции.
Пр инцип ом с упер пози ци и называется свойство, заключающееся
в том, что реакция системы на сумму воздействий равна сумме реакций
этой же системы на каждое из воздействий в отдельности.
Покажем, что линейные динамические системы, движения которых
описываются уравнениями (2.127), (2.128), удовлетворяют этому прин-
ципу. С этой целью положим
)()()(
21
tgtgtg
+=
и подставим в равенст-
во (2.133), которое описывает движения рассматриваемых динамических
систем. Тогда при
0
0
=
t
и
0
=
D
будем иметь
( )
=
∫
ττ+τ+=
τ−
t
tAAt
dggBCexCety
0
21
)(
0
)()()(
∫
ττ+
∫
ττ+=
τ−τ−
t
tA
t
tA
At
dBgCedBgCexCe
0
2
)(
0
1
)(
0
)()(
.
92
Отсюда следует, что
)()()()(
21
tytytyty
вынвынсв
++=
, (2.136)
где
)(ty
св
,
)(
1
ty
вын
и
)(
2
ty
вын
– реакции рассматриваемой системы на
каждое воздействие
0
x
,
)(
1
tg
и
)(
2
tg
в отдельности.
Из соотношения (2.136) непосредственно следует, что линейные ди-
намические системы удовлетворяют принципу суперпозиции.
В заключение приведем простой пример решения неоднородной
системы дифференциальных уравнений (2.127) и (2.128) с помощью пе-
реходной матрицы
At
e
.
Пример 2.20. Найти решение неоднородной системы дифференци-
альных уравнений следующего вида:
,
1
0
20
01
gxx
+
−
−
=
&
gxy
2]11[ +=
,
где
t
eg
3
5
−
=
, а вектор начальных условий
]11[
0
−=
T
x
при
0
0
=t
.
Решение. Так как матрица А диагональная, то по формуле (2.113)
−
−
=
t
t
At
e
e
e
2
0
0
.
Применяя формулу Коши (2.132) при
0
0
=t
, найдем
∫
=ττ+=
τ−
t
tAAt
dBgexetx
0
)(
0
)()(
=τ
∫
+
−
=
τ−
τ−−
τ−−
−
−
de
e
e
e
e
t
t
t
t
t
3
0
)(2
)(
2
5
1
0
0
0
1
1
0
0
∫
τ
+
−
=
∫
τ
+
−
=
τ−−
−
−
τ−τ−−
−
−
t
t
t
t
t
t
t
t
dee
e
e
d
ee
e
e
0
2
2
0
3)(2
2
0
5
0
5
.
Отсюда, следует
93
−
−
=
−−
−
tt
t
ee
e
tx
32
56
)(
.
Итак, переменные состояния рассматриваемой системы описывают-
ся выражениями
t
etx
−
−=)(
1
,
tt
eetx
32
2
56)(
−−
−=
.
Подставляя
)(tx
в уравнение выхода, получим
ttttt
tt
t
eeeee
ee
e
ty
3323
32
105610
56
]11[)(
−−−−−
−−
−
+−+−=+
−
−
=
или окончательно
ttt
eeety
32
56)(
−−−
++−=
.
Обратим внимание, что решение заданной системы уравнений
включает три экспоненты, причем две первые из них имеют показатели,
совпадающие с собственными числами матрицы А системы, а третья яв-
ляется экспонентой, содержащейся во входном воздействии. Ни каких
других функций решение не содержит.
Как отмечалось выше, экспоненты, показатели которых совпадают с
собственными числами матрицы А из уравнения (2.127) некоторой дина-
мической системы, называются модами этой системы. Аналогично, экс-
поненты или другие функции, содержащиеся в воздействии, можно на-
звать модами воздействия. Поэтому составляющими решения системы
дифференциальных уравнений всегда являются моды или системы и
(или) воздействия. Это свойство решений линейных систем дифференци-
альных уравнений является всеобщим и, как видно, вытекает из формулы
Коши. Причем, если у матрицы А некоторой динамической системы,
описываемой уравнениями (2.127), (2.128), имеются вещественные
µ
λ
и
комплексные
iii
jω±σ=λ
собственные числа, то в решениях
)(
tx
и
)(
ty
этой системы наряду с модами, обусловленными воздействием
)(
tg
, в об-
щем случае, будут содержаться моды самой системы вида
t
etC
µ
λ
µ
)(
и
)sin()(
ii
t
i
tetC
i
ϕ+ω
σ
, где
)(tC
µ
,
)(
tC
i
– некоторые функции времени, а
i
ϕ
– постоянные величины.
94
§ 2.5. Определение реакции динамических систем
Модели воздействий. Реальные динамические системы подвер-
гаются влиянию воздействий различных видов. Выходная переменная
некоторой системы, вызванная некоторым воздействием, называется ре -
ак цие й системы на это воздействие. В случае воздействия произвольно-
го вида определение реакции даже линейной системы затруднительно.
Поэтому анализ линейных динамических систем обычно проводится при
простейших видах воздействий. Основанием для такого подхода является
свойство суперпозиции линейных систем, а также возможность пред-
ставления воздействия сложной формы в виде суммы (линейной комби-
нации) воздействий простейших видов. Наиболее часто употребляемые
для исследования динамических систем воздействия называются ти по-
вы ми в оз дей ств ия ми . Перейдем к рассмотрению их математических
моделей.
Ступенчатое воздействие. Это воздействие описывается выраже-
нием
)(1)(
0
tgtg =
, (2.137)
где
)(1 t
– ступенчатая единичная функция (функция Хевисайда). Сту-
пенчатая единичная функция определяется соотношением
<
≥
=
0,0
0,1
)(1
t
t
t
(2.138)
т.е. при всех отрицательных t эта функция равна нулю, а при всех
0
≥
t
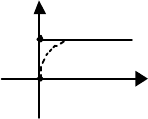
она равна единице. График ступенчатого воздействия приведен на рис.
2.10. Как видно, это воздействие также равно нулю при всех значениях
0
<
t
, а при
0
=
t
мгновенно принимает значение
0
g
и затем остается постоянным. В действитель-
ности это невозможно. Поэтому ступенчатое воз-
действие – это идеализация реальных воздейст-
вий, изменяющихся так, как показано на рис. 2.10
пунктиром. Такое реальное воздействие можно
описать выражением
)1()(
~
/
0
τ−
−=
t
egtg
,
где число
1
<<
τ
. Другими словами, ступенчатое воздействие – это мо-
дель реальных воздействий, которые изредка и очень быстро принимают
g
0
0
t
g
Рис. 2.10
95
новые постоянные значения. Таким образом изменяется, например, со-
противление нагрузки
н
R
рассмотренного выше электрического генера-
тора постоянного тока.
Выражение
pgpg /)(
0
=
, которое является изображением по Лап-
ласу ступенчатого воздействия, представляет собой операторную форму
модели ступенчатого воздействия.
Очень часто рассматриваются модели воздействий в виде некоторо-
го полинома
)(pG
. Здесь
)(pG
это характеристический полином неко-
торого однородного дифференциального уравнения, решение которого
при определенных начальных условиях совпадает с воздействием
)(tg
при всех
0
≥
t
. Данный полином
)(pG
называется
p
K
-изображением
воздействия
)(tg
. Это название связано с именем академика В.С. Куле-
бакина, который впервые предложил использовать полином
)(pG
при
создании инвариантных систем автоматического управления.
Полином
)(pG
, представляющий собой
p
K
-изображение некото-
рого воздействия
)(tg
, всегда совпадает со знаменателем изображения
по Лапласу
)(pg
этого воздействия.
В случае ступенчатого воздействия
p
K
-изображение, очевидно,
имеет вид
ppG
=
)(
.
Нетрудно записать соответствующее дифференциальное уравнение. В
изображениях по Лапласу это уравнение имеет вид
0)(
=
ppg
. Переходя в
нём к оригиналам, получим искомое дифференциальное уравнение
0)(
=
tg
&
.
Общее решение
Сtg
общ
=)(
этого уравнения при
0
g
С
=
, очевидно,
совпадает со ступенчатым воздействием
)(1)(
0
tgtg =
при всех
0
≥
t
.
В переменных состояния ступенчатое воздействие описывается
уравнениями
0=
g
x
&
,
g
xg =
.
Толчковое воздействие. Это также идеальное воздействие. Оно
описывается выражением
)()(
0
tgtg δ=
, (2.139)
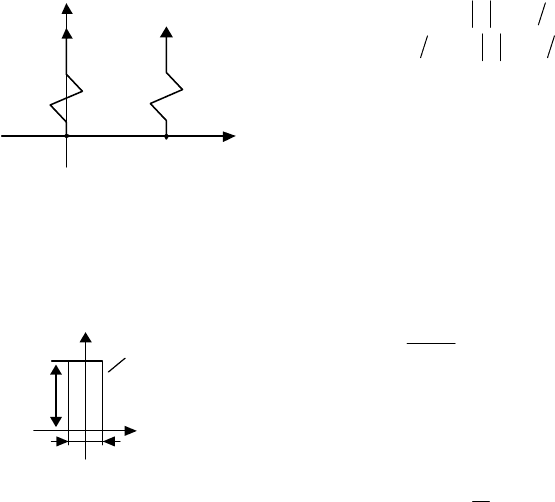
96
где
)(t
δ
– дельта-функция, которая была введена физиком П. Дираком.
Она определяется выражениями
≠
=∞
=δ
0,0
0,
)(
t
t
t
(2.140)
1)( =δ
∫
∞
∞−
dtt
. (2.141)
На рис. 2.11 (слева) приведено условное графическое обозначение
обычной дельта-функции
)(t
δ
, а справа запаздывающей дельта-функции
)(
1
tt −δ
, которая не равна нулю лишь в точке
1
tt =
.
Дельта-функцию
)(t
δ
можно рассматривать как предел прямо-
угольного импульса
)(tS
, показанного на рис. 2.12 и описываемого
выражениями
∆≤∆
∆>
=∆
2,1
2,0
),(
ttt
tt
ttS
,
при
∞
→
∆
t
, т.е.
)(),(lim
0
tttS
t
δ=∆
→∆
.
Таким образом, толчковое воздейст-
вие (2.139) является идеализацией кратко-
временных внешних воздействий, ударов,
порывов ветра и т.п., то есть импульсных
воздействий.
Можно также считать (не строго), что
)(t
δ
– это производная по
времени от ступенчатой единичной функции
)(1 t
, т.е.
dt
td
t
)(1
)( ≈δ
.
Это позволяет, в частности, найти изображение
по Лапласу дельта-функции
)(t
δ
. Пользуясь извест-
ным свойством преобразования Лапласа, получим
1
1
)}(1{)( =⋅==δ
p
ptpLp
,
δ
(t-t
1
)
δ
(t)
t
1
0 t
Рис.2.11
1/
∆
t
∆
t
S
(
t
)
Рис. 2.12

97
так как
ptL 1)}(1{ =
.
Экспоненциальное воздействие. Это воздействие описывается экс-
понентой, т.е.
t
egtg
α
=
0
)(
.
Графики его изменения во времени при различных значениях показа-
теля экспоненты
α
приведены на рис. 2.13.
Изображение по Лапласу экспоненциального воздействия имеет вид
α−
=
p
g
pg
0
)(
.
Следовательно,
p
K
-изображение экспоненциального воздействия
α
−
=
ppG )(
, а его уравнения в переменных состояния имеют вид
gg
xx α=
&
,
g
xg =
.
Полиномиальное воздействие. Это
воздействие описывается полиномом от t ,
который имеет вид
r
r
tgtgtggtg K+++=
2
210
)(
, (2.142)
где
i
g
– параметры, r – степень полинома
(2.142), а величина
1
+
r
– порядок данного
воздействия.
Таким образом, порядок полиномиального воздействия всегда на
единицу больше степени полинома, описывающего это воздействие.
Фактически величина
1
+
r
это порядок такой динамической системы,
выходная переменная которой при соответствующих начальных условиях
(в соответствии с определением
p
K
-изображения) совпадает с данным
воздействием при всех
0
≥
t
.
Различают следующие полиномиальные воздействия.
• линейное воздействие (r = 1):
tggtg
10
)( +=
.
α
=0
α
>0
α
<0
g
0
t
g
0
Рис. 2.13

98
Графики этого воздействия при различных знаках параметра
1
g
приведены на рис. 2.14.
p
K
-изображение этого воздействия
2
)( ppG =
,
т.е. его порядок
21
=
+
=
rn
;
• параболическое воздействие (r = 2):
2
210
)( tgtggtg ++=
.
p
K
-изображение этого воздействия
3
)( ppG =
, а порядок
3
1
=
+
=
rn
.
Уравнения в переменных состояния поли-
номиального воздействия (2.142) можно записать следующим образом:
gg
xx
=
0000
1000
0100
0010
K
K
MOMMM
K
K
&
,
1g
xg =
, (2.143)
где
g
x
– вектор размерности
1
+
=
rn
.
Модель – полиномиальное воздействие используется для описания
сложных, не колебательных воздействий, таких как изменения темпера-
туры, давления, координат движущихся объектов, средних значений слу-
чайных нестационарных воздействий и т.п.
Частным случаем полиномиального воздействия, очевидно, является
рассмотренное выше ступенчатое воздействие.
Гармоническое воздействие. Это колебательное воздействие, опи-
сывается функциями
)sin()( ϕ+ω=
tgtg
m
или
)cos()( ϕ+ω=
tgtg
m
. (2.144)
Соответствующие графики гармонических воздействий при
0
=
ϕ
приведены на рис. 2.15. Воздействия данного типа характеризуются сле-
дующими параметрами: амплитудой
m
g
, круговой частотой
f
π
=
ω
2 ]/[ срад
, фазой
ϕ
],[ градрад
и периодом
ωπ=
2T ][с
, где
Tf 1
=
][
1
−
с
– число колебаний в секунду.
g
0
g
1
>0
g
1
<0
g
t0
Рис. 2.14

99
Очень часто вместо синусоидального или косинусоидального воз-
действий (2.144) применяется ко мпл екс ное воздей ст ви е
)(
)(
ϕ+ω
=
tj
m
egtg
. Это воздействие часто называется просто «к ом -
плек с», причем обычно полагают
0
=
ϕ
.
В изображениях по Лапласу гармониче-
ские воздействия описываются выражениями
22
)(
ω+
=
p
p
gpg
m
или
22
)(
ω+
ω
=
p
gpg
m
,
т.е. эти модели учитывают только амплитуду и частоту воздействия.
На основании двух предыдущих выражений заключаем, что
p
K
-
изображением гармонических воздействий с частотой
ω
является полином
22
)( ω+=
ppG
. (2.145)
Соответствующие уравнения в переменных состояния можно запи-
сать следующим образом:
gg
xx
ω−
=
0
10
2
&
,
1g
xg =
. (2.146)
Две последние модели (2.145) и (2.146) являются, очевидно, наибо-
лее общими, так как включают только частоту гармонического воздейст-
вия.
Гармонические, как и любые другие рассмотренные выше воздейст-
вия, по о пре де лени ю, существуют только при
0
≥
t
или, в более об-
щем случае, при
0
tt ≥
. При всех
0
<
t
или
0
tt <
они равны нулю, так
как считается, что динамическая система начинает функционировать,
начиная с момента времени
0
=
t
или, в более общем случае, начиная с
момента времени
0
tt =
.
Определение реакции систем на типовые воздействия. Будем
считать, что уравнения динамической системы, схема которой показана
на рис. 2.16, имеют вид
g
g
m
0
T
t
Рис. 2.15

100
bgAxx
+
=
&
, (2.147)
gxcy
T
β+=
. (2.148)
Начальные условия
0
)0( xx =
, воздействие
)(
tgg
=
, матрица
At
e
, векторы b, c и число
β
– заданы. Необходимо найти выходную переменную системы. По
формуле (2.133) можно записать
)()()(
0
)(
0
tgdbgecxecty
t
tATAtT
β+ττ+=
∫
τ−
. (2.149)
Реакция на ступенчатое воздействие. Пусть
)(1
0
tgg =
,
0det
≠
A
,
и
1
−
A
определена. Тогда с учетом свойств матрицы
At
e
из выражения
(2.149) имеем
)(1)(
00
0
0
tgbgdeecxecty
t
AAtTAtT
β+τ+=
∫
τ−
.
Найдем интеграл в этом выражении
)(
1
0
1
0
EeAeAde
At
t
A
t
A
−−=−=τ
−−τ−−τ−
∫
.
Подставляя в предыдущее равенство, получим
=β+−−=
−−
)(1)()(
00
1
0
tgbgEeAecxecty
AtAtTAtT
)(1)(
00
1
0
tgbgeEAcxec
AtTAtT
β+−−=
−
или окончательно
44 344 21444 3444 21
)(
0
1
)(
0
1
0
)()()(
ty
T
ty
AtT
устпер
gbAcbgAxecty
−−
−β++=
,
0
≥
t
. (2.150)
Как видно, решение состоит из двух составляющих, показанных на
рис. 2.17.
W
g y
Рис. 2.16
