Гаспер Б.С., Липатов И.Н. ИВС и АСУТП. Учебное пособие

Подождите немного. Документ загружается.

Случайные сигналы делятся на: стационарные и нестационарные. У ста-

ционарных сигналов вероятностные характеристики не зависят от времени (посто-

янны), что позволяет значительно упростить их математическое описание.

Во множестве стационарных сигналов выделяется подмножество эргодиче-

ских сигналов, не совсем строгое определение которых можно дать следующим

образом. Вероятностные характеристики случайных сигналов могут быть получе-

ны либо усреднением во времени, т.е. путем рассмотрения всех значений одной

реализации сигнала, либо усреднением по множеству (ансамблю) реализаций, т.е.

путем рассмотрения значений всех реализаций случайного сигнала в один и тот

же момент времени. Сигналы, для которых вероятностные характеристики не за-

висят от способа усреднения (по времени и ансамблю) называются эргодически-

ми.

Все случайные сигналы в конечном итоге классифицируются по виду зако-

на распределения плотности вероятности, который является полной и исчерпы-

вающей характеристикой любого случайного сигнала.

3.2.Формы аналитического описания сигналов

Возможна форма представления сигналов с помощью спектров. Рассмот-

рим ее для непрерывных одномерных сигналов общего вида x(

) (

- некоторый

аргумент, в частном случае время t).

При этом сигнал на заданном интервале его определения [

min

max

] рас-

сматривается как совокупность элементарных сигналов

(

), умноженных на ко-

эффициенты c

и составляющих систему функций {

(

)} определенного типа:

xc() ()

ξϕξ

αα

∞

∑

. (3.1)

При этом система функций {

(

)} называется базисной, а представление

сигнала в виде (3.1) - его разложением по системе базисных функций или обоб-

щенным рядом (многочленом). Если сигнал x(

) является комплексным, то и ко-

эффициенты c

и система базисных функций {

(

)} также будут являться ком-

плексными.

Если система функций выбрана, то сигнал полностью характеризуется на-

бором (вектором) спектральных коэффициентов {c

} - его спектром.

В общем случае ряд (3.1) для непрерывных сигналов содержит бесконечное

число членов. При практических расчетах такой ряд обычно ограничивают (усе-

кают). В этом случае представление сигнала будет приближенным

xx c

() () ()

ξξ ϕξ

αα

−

∑

(3.2)

и имеет место аппроксимация сигнала x(

) конечным рядом (3.2).

Выбирая приближенное описание сигнала, естественно, стремятся к тому,

чтобы оно, в определенном смысле, наилучшим образом соответствовало ориги-

налу. При этом каждый раз необходимо формулировать критерий приближения,

так как в выражение «наилучшее приближение» можно вкладывать различный

смысл.

Приведем наиболее широко применяемые критерии приближения (сходи-

мости).

1. Можно потребовать, чтобы максимальное значение погрешности ап-

проксимации

Δ() () ()

ξξ ξ

=−xx (3.3)

было минимальным на заданном интервале определения функции x(

Этот вид аппроксимации, при котором минимизируется величина

Δ()

max

, называется равномерным приближением.

2. В качестве критерия приближения можно выбрать среднюю погреш-

ность

xxd=−

∫

() ()

min

max

ξξξ

, (3.4)

где T =

max

min

Такая аппроксимация называется приближением в среднем.

3. Если в качестве меры представления принимается минимум среднеквад-

ратичной погрешности

[]

σξξξ

=−

∫

xx d() ()

min

max

, (3.5)

то такой вид аппроксимации называется приближением в среднеквадра-

тическом.

Существуют и другие критерии приближения [1,2]. В большинстве техни-

ческих применений преимущественное распространение получил среднеквадрати-

ческий критерий, учитывающий интегральный эффект - ошибку, накопленную на

всем интервале определения сигнала, и в большинстве случаев лучше соответст-

вующий физическому смыслу исследуемых явлений. Кроме того, что тоже нема-

ловажно, теория, основанная на этом критерии, имеет наиболее простой и удоб-

ный для практики вид.

Все рассмотренные критерии приближения взаимосвязаны. Если ряд (3.2)

сходится к x(

) равномерно, то он тем более сходится среднеквадратически. Из

среднеквадратической сходимости вытекает сходимость в среднем.

Для того, чтобы разложение сигнала в форме (3.1) было возможным, сис-

тема базисных функций (СБФ) должна удовлетворять ряду требований:

1) Быть упорядоченной системой линейно независимых функций.

2) Быть полной, для того, чтобы по выбранной системе функций можно было раз-

ложить любой сигнал из заданного множества.

3) Число линейно независимых функций в полной системе должно быть равным

размерности рассматриваемого множества сигналов, т.е. количеству чисел, с

помощью которых можно выбрать любой сигнал из этого множества. Когда

рассматривается множество непрерывных сигналов произвольной формы, то их

размерность бесконечно велика и в этом случае СБФ должна содержать также

бесконечно большое число линейно независимых функций.

Наиболее удобно производить разложение сигналов, если базисная система

{

(

)} является ортогональной на интервале определения сигнала [

min

max

]. Ус-

ловие ортогональности двух различных базисных функций заключается в равенст-

ве нулю их взаимной мощности:

∫

max

min

)()(

ξξϕξϕ

, (3.6)

где символ Кронекера и мощность

-й базисной функции

пи

⎧

⎨

⎩

≠

;

(3.7)

∫

max

min

)(

αα

ξξϕ

. (3.8)

Интервал определения ортогональных базисных функций называется также

интервалом ортогональности

Если система ортогональных функций полная, то к ней нельзя добавить ни

одной новой функции, которая была бы ортогональна одновременно ко всем дру-

гим функциям данной системы. Известно, что любую систему линейно независи-

мых функций можно ортогонализировать, т.е. преобразовать в ортогональную

систему [1].

Представление сигналов с помощью ортогональных СБФ обладает

тем

важным свойством, что повышение порядка аппроксимирующего многочлена все-

гда улучшает аппроксимацию по сравнению с представлением сигналов неортого-

нальными СБФ. Если при N→∞ многочлен x

()

[см. (3.2)] сходится к x()

, то

()

совпадает с x()

в рамках выбранного критерия приближения.

Система ортогональных функций называется также нормированной

, если

мощности всех базисных функций равны единице (в этом случае СБФ называется

еще ортонормированной)

ϕξξ

()

min

max

∫

. (3.9)

Любую систему ортогональных функций можно нормировать, если разде-

лить каждую базисную функцию на ее мощность.

При представлении сигналов в форме (3.2) необходимо решать вопрос о

способе вычисления спектральных коэффициентов. Он во многом будет зависеть

от используемого метода аппроксимации (вида принятого критерия сходимости).

В случае применения среднеквадратического критерия коэффициенты c

, выби-

рают таким образом, чтобы среднеквадратическая ошибка σ была минимальной.

Это достигается с помощью обобщенной формулы Фурье расчета спектра:

c [1/(Q T

)]·

∫

max

min

)()(

ξξϕξ

. (3.10)

Очевидно, что среднеквадратическая аппроксимация имеет смысл тогда,

когда мощность сигнала

x()

и функций

(

) на интервале аппроксимации имеет

конечное значение. В случае комплексных базисных систем в формуле (3.10) рас-

чета спектра должна стоять комплексно-сопряженная функция

ϕξ

().

Увеличивая неограниченно число членов в аппроксимирующем многочле-

не с коэффициентами в форме (3.10), получим в пределе равенство

()

= x()

выполняемое при

σ →∞. При этом аппроксимирующий многочлен примет вид

бесконечного ряда, называемого обобщенным рядом Фурье.

В спектральном представлении (3.1) и в формуле расчета спектра (3.10) ба-

зисные функции являются функциями двух переменных

, а спектральные ко-

эффициенты - функциями переменной

. Это приводит к симметрии выражений

(3.1) и (3.10), называемых соответственно прямым и обратным преобразованием

Фурье, из которой следует математическое равноправие функций

x()

и с

как

различных форм представления сигнала. Для рядов Фурье справедливо равенство

Парсеваля [3]:

∑

∫

∞

max

min

)(

ξξϕ

αα

с . (3.11)

Так как правая часть этого равенства определяет мощность сигнала при его

представлении с помощью спектров, а левая - его мощность при записи в виде ма-

тематической функции, то равенство Парсеваля отражает эквивалентность двух

форм представления сигналов с физической (энергетической) точки зрения. Вы-

полнение равенства Парсеваля свидетельствует также о полноте ортогональной

СБФ

Рассмотрим представление с помощью спектров дискретных сигналов. Ре-

шетчатая функция

x(i), i ∈ [0, N] записывается в виде обобщенного дискретного

ряда

∑

−

)()(

iсix

αα

(3.12)

по любым полным и ортогональным системам решетчатых базисных функций

{

(i)}. При этом моменты отсчетов базисных функций должны совпадать с мо-

ментами отсчетов раскладываемых сигналов.

Условия ортогональности и нормированности дискретных СБФ определя-

ются уравнениями

∑

−

)()(

ϕϕ

αα

; (3.13)

∑

−

1)(

αα

, (3.14)

а равенство Парсеваля для дискретных сигналов имеет вид

∑∑

−

)(

αα

. (3.15)

Для дискретных функций, удовлетворяющих условию

∑

−

∞<

)(

справедлива следующая формула для определения спектра:

c [1/(Q N

)]·

∑

−

)()(

iix

. (3.16)

Формулы (3.12) и (3.16) представляют собой дискретные преобразования

Фурье.

3.3. Системы базисных функций

Один и тот же сигнал может быть разложен по различным СБФ или, что

одно и то же, рассмотрен в различных системах координат. При этом внутренние

закономерности сигналов не могут нарушаться при изменении системы коорди-

нат. Однако спектральному анализу в различных СБФ соответствует различная

физическая интерпретация и, что особенно важно, различная практическая реали-

зация. Так, например, технические характеристики (точность, быстродействие, за-

траты памяти и оборудования) цифровых фильтров, построенных в спектральной

области, зависят от применяемых СБФ и для

различных систем существенно раз-

личны. В соответствии с этим, при решении практических задач целесообразно

подбирать наиболее подходящие СБФ. Выбор базиса во многом обусловлен спе-

цификой решаемых задач и требованиями, предъявляемыми при их решении.

Полных и ортогональных СБФ существует бесчисленное множество. Да-

дим краткий обзор некоторых известных СБФ, применяемых в настоящее

время в

теории и практике обработки сигналов.

Системы единичных функций

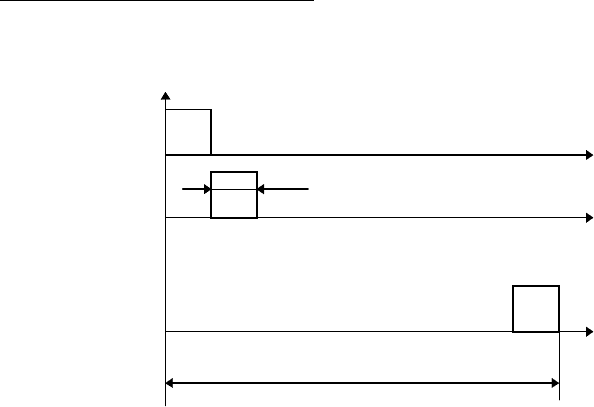
. Два прямоугольных импульса, не перекры-

вающие друг друга, ортогональны. Поэтому система прямоугольных импульсов

(рис. 3.6), приставленных друг к другу и заполняющих интервал [t

, t

], будет ор-

тогональной системой.

Рис. 3.6

Такая система полна только для подмножества ступенчатых сигналов с шириной

ступени

t, где

t - длительность импульсов, N = T /

t - число импульсов на рас-

сматриваемом интервале. Система таких функций будет полна для любого непре-

рывного сигнала при

t → 0 и N → ∞. В этом случае она превращается в систему

единичных импульсов {u

(t)}, имеющих единичную амплитуду и бесконечно ма-

лую длительность, положение которых определяется сдвигом по оси

αΔ

t = t при

→ 0,

→ ∞. Система функций {u

(t)} является полной ортогональной системой.

Из нее дискретизацией можно получить систему дискретных единичных

функций {u

(i)}, каждая из которых имеет вид единичного импульса бесконечно

малой длительности и аналитически записывается в виде

()=

⎧

⎨

⎩

пи

;

≠

(3.17)

N-1

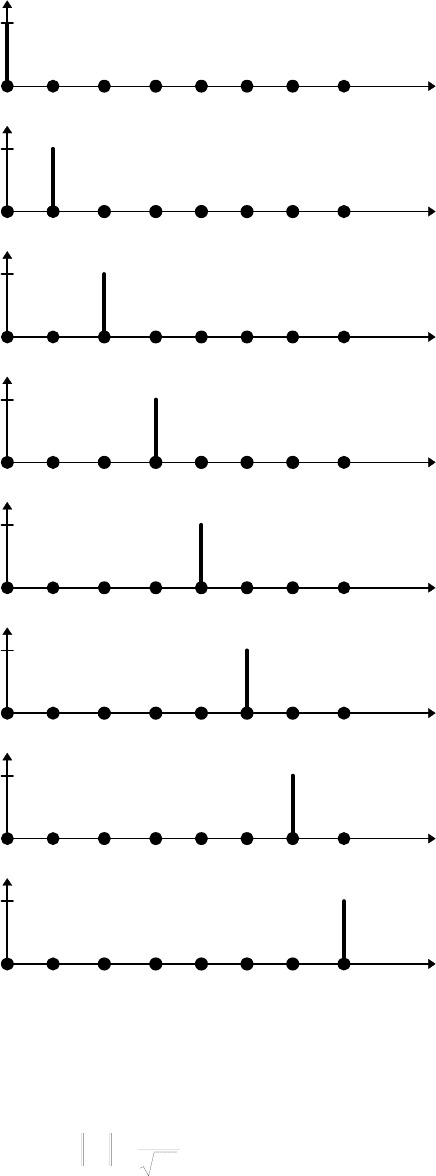
Такая система определена на целочисленном интервале [0, N). Для N=8 она

приведена на рис. 3.7.

Рис. 3.7

Система {u

(i)} в форме (3.17) является ненормированной, и ее норма (ко-

рень квадратный из мощности)

. (3.18)

Эта система представляет собой полную СБФ, служащую для разложения

дискретных сигналов произвольной формы.

Система дискретных единичных функций обладает тем свойством, что ее

0 1 2 34567

спектральный коэффициент с номером

совпадает со значением сигнала в точке i

его интервала определения, т.е.

= x(

). (3.19)

Подобным свойством обладает и непрерывная система {u

(t)}. Это свойст-

во единичной системы позволяет проиллюстрировать взаимосвязь между пред-

ставлением сигнала в области аргументов и спектральной области. В соответствии

с ним представление в области аргумента можно рассматривать как частный слу-

чай спектрального представления в единичном базисе. Это позволяет получать ре-

зультаты в области аргументов, используя более общие результаты

в спектраль-

ной области.

Системы тригонометрический базисных функций

. Система тригонометри-

ческих функций {cos(k

) , sin(k

)} = { 1, sin(

), cos(

), sin(2

), cos(2

), ...} является

полной ортогональной системой с интервалом ортогональности [-

], либо [0,

]. Система является периодической с периодом 2

и ненормированной (норма

равна 1/

2). Проведя нормирование на ее основе, можно получить полную орто-

нормированную систему { 1,

2 sin(

), 2 cos(

), 2 sin(2

), 2 cos(2

), ...}.

Дискретный аналог этой СБФ - полная ортонормированная система дис-

кретных тригонометрический функций

,)2cos(,

)1(2

cos2,,

cos2,

sin2,1

sin2,

cos2

⎭

⎬

⎫

⎩

⎨

⎧

−

⎭

⎬

⎫

⎩

⎨

⎧

ππππ

определенная на интервале [-N/2, N/2) или [0, N).

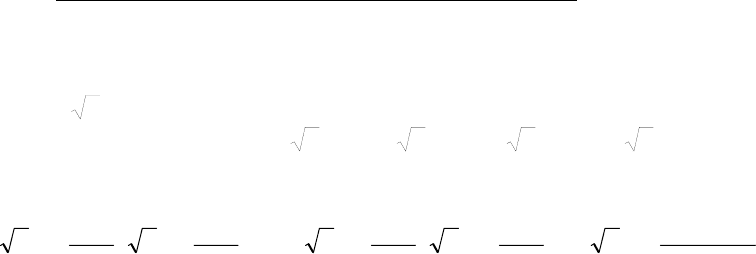
В качестве примера на рис.3.8 приведена система из восьми функций с ин-

тервалом определения [-4, 4).

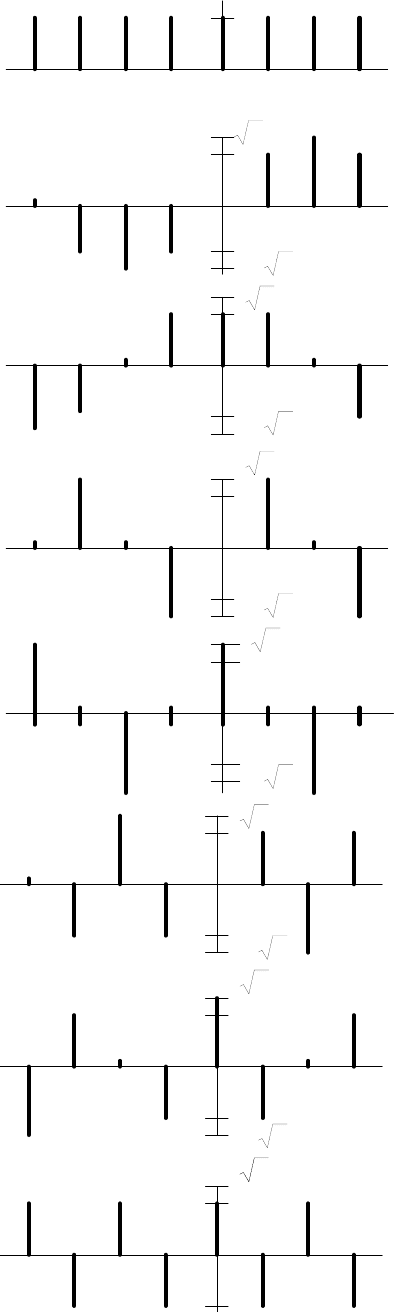
Рис. 3.8

cos

-1

sin

cos

− 2

-1

− 2

cos

-4-3-2-10123

sin

cos

-1

sin

− 2

-1

− 2

cos

-1

− 2

Системы комплексных экспоненциальных функций. Полной ортогональной

системой на интервале [-

] или любом другом интервале длительностью 2

яв-

ляется система комплексных экспоненциальных функций

{

}

. Это нормирован-

ная периодическая система с периодом 2

. Для нее характерно свойство мультип-

ликативности, заключается в том, что произведение двух любых ее функций явля-

ется также функцией этой системы:

ll l

jk jm jl

ξξ ξ

, (3.20)

где

l = k + m.

Дискретный аналог этой системы - система дискретных комплексных экс-

поненциальных функций

⎧

⎨

⎩

⎫

⎬

⎭

, обладающая свойствами полноты, нормирован-

ности, ортогональности и мультипликативности на интервале, содержащим

N от-

счетов. Зависимости (3.12) и (3.16) ряда и коэффициентов Фурье при использова-

нии в качестве базиса системы дискретных комплексных экспоненциальных

функций называются дискретными преобразованиями Фурье[3]

xi c

()=

−

∑

; (3.21)

−

∑

()l

, (3.22)

где

−

⎧

⎨

⎩

⎫

⎬

⎭

- система комплексно-сопряженных экспоненциальных функций, оп-

ределенных на интервале в

N точках.

Спектр

в базисе

⎧

⎨

⎩

⎫

⎬

⎭

является комплексной функцией. Системы ком-

плексных экспоненциальных функций широко применяются при решении различ-

ных технических и научных задач и достаточно подробно описаны в литературе

[1,2,3].

Полиномиальные базисные системы

. К ним относят системы, построенные

на основе ортогональных полиномов [4]. Рассмотрим две такие системы, опреде-

ленные на конечных интервалах.

Полиномы Чебышева

. На интервале [-1, 1] можно построить полную орто-

нормальную систему

ϕξ π ξ

T() ( ) ()=

−

, n=0,1,2,..., (3.23)

где

(

) - полиномы Чебышева, задаваемые следующим образом:

(

)=1,

Tnn

( ) cos( arccos( )),

ξξ

=⋅ ≥

−

. (3.24)

Полиномы Чебышева обладают тем важным свойством, что из всех поли-

номов n-ой степени, имеющих коэффициент при

, равный единице, полином

Чебышева T

(

) наименее отклоняется от нуля на интервале [-1, 1]. При n≥3 значе-

ние T

(

) можно вычислять по рекуррентной формуле

TT T

nn n

() () . ()

−

−−12

025 . (3.25)

Полиномы Лежандра

. Нормированные и ортогональные функции

ϕξ

()=

ϕξ ξ

()=

ϕξ ξ ϕξ ξ

() , , () ()=−

⎡

⎣

⎢

⎤

⎦

⎥

P образуют

полную систему базисных функций на отрезке [-1,1]. Здесь {P

(

)} - полиномы

Лежандра, определяемые по формуле по формуле

()

=−

(3.26)

или по рекуррентной зависимости

(

) = (2n - 1)

n-1

(

) - (n - 1)P

n-2

(

). (3.27)

Непосредственная дискретизация непрерывных СБФ, построенных на ос-

нове ортогональных полиномов, образует системы дискретных функций с нерав-

ноотстоящими отсчетами. В этом смысле непрерывные полиномы не имеют ре-

шетчатых аналогов. Однако в классе полиномиальных функций можно построить

решетчатые полиномы, используя непосредственное представление их аргумента

в виде дискретной переменной. Среди таких функций конечный

интервал опреде-

ления имеют функции дискретных систем Чебышева, Кравчука, Шарлье и Мейк-

снера.

Функции систем этого класса ортогональны на интервале [0, N) и являются

ненормированными. Для каждой системы известны рекуррентные соотношения,

позволяющие строить аналитические описания функций при различных значениях

номера функции

и числа отсчетов N. Данные аналитические описания можно

представить в форме обобщенных степенных полиномов

pol i a i

()=

∑

, (3.28)

где a

- коэффициенты, зависящие от конкретного типа системы.

От типа системы зависят и нормы базисных функций, поскольку эти систе-

мы не являются нормированными. Например, для системы Чебышева коэффици-

енты и норма записываются как [3]

kkNNNk

−+

−−− −

()( )!

(!)( )!( )( ) ( )

; (3.29)

pol i

NN N

NNNN

αα

()

()( )

()()()()

−

+−− −

21 1 2

. (3.30)

Проведя нормирование, можно построить нормированные системы дис-

кретных полиномов. Для нормированного базиса Чебышева первые три его функ-

ции представляются следующим образом:

⎪

⎭

⎪

⎬

⎫

−+−−−−

−−

)]1(6)2(6)2)(1[(

)1)(2(

)(

)21(3

)(,1)(

iiNiNN

ipol

ipolipol

(3.31)

и для N=8 приведены на рис. 3.9.