Гашков С.Б. Современная элементарная алгебра в задачах и решениях
Подождите немного. Документ загружается.


§ 4.9. Решение методом Лагранжа уравнений четвертой степени 241
Однако заметим, что некоторые перестановки дают выражения, про
-
порциональные t, причем коэффициенты пропорциональности являются
корнями четвертой степени из 1.
Это происходит при циклической перестановке Π = x
1
→x
2
→x
3
→
→x
4
→x
1
и, следовательно, еще при двух перестановках, являющихся
ее степенями, а именно при перестановках Π
2
, Π
3
(перестановка Π
4
уже
является тождественной). Можно это проверить и непосредственно, на
-
пример, заметив, что перестановка Π
2
меняет местами переменные x
1
и x
3
, а также переменные x
2
и x
4
, и выражение t при этом меняет знак
на противоположный.
Заметим, что при этих перестановках выражение t
4
вообще не меня
-
ется.
Упражнение 107. Проверьте, что любая другая перестановка не об
-
ладает этим свойством.
Упражнение 108. Проверьте, что при всех 24 перестановках выра
-
жение t
4
принимает ровно 24
/
4 = 6 значений:
t
4
1
= [(x
1
−x
2
) + (x
3
−x
4
)i]
4
; t
4
2
= [(x
1
−x
3
) + (x
2
−x
4
)i]
4
;
t
4
3
= [(x
1
−x
4
) + (x
2
−x
3
)i]
4
; t
4
4
= [(x
1
−x
2
) + (x
4
−x
3
)i]
4
;
t
4
5
= [(x
1
−x
3
) + (x
4
−x
2
)i]
4
; t
4
6
= [(x
1
−x
4
) + (x
3
−x
2
)i]
4
.
Эти значения являются корнями уравнения шестой степени, коэффи
-
циенты которого полиномиально выражаются через коэффициенты ис
-
ходного уравнения. Получившееся уравнение шестой степени можно раз
-
ложить на два кубических. Однако этот способ требует слишком много
вычислений.
Попытаемся найти более удобные выражения, чем t(x
1
, x
2
, x
3
, x
4
). Для
этого рассмотрим подробнее метод разложения на два множителя, при
-
мененный Феррари.
Его идея состоит в том, чтобы представить левую часть уравнения
x
4
+ ax
3
+ bx
2
+ cx + d = 0 в виде разности двух квадратов. Тогда ее
можно будет разложить на два множителя второй степени, и решение
уравнения приведется к решению двух квадратных уравнений. Для этого
левую часть представим в виде
x
2
+
a
2
x +
y
2
2
−
a
2
4
x
2
−
ayx
2
−
y
2
4
−yx
2
+ bx
2
+ cx + d =
=
x
2
+
a
2
x +
y
2
2
−
h
a
2
4
+ y −b
x
2
+
ay
2
−c
x +
y
2
4
−d
i
,
где y
––
вспомогательная неизвестная, которую подберем так, чтобы вы
-
ражение в квадратных скобках оказалось квадратом линейного двучлена.
16 Гашков
242 Глава IV. Алгебраические уравнения
Для этого необходимо и достаточно выполнения условия
ay
2
−c
2
−4
a
2
4
+ y −b
y
2
4
−d
= 0.
Это условие есть кубическое уравнение относительно y. Оно называется
резольвентой Феррари.
После раскрытия скобок уравнение преобразуется к виду
y
3
−by
2
+ (ac −4d)y − (c
2
+ a
2
d −4bd) = 0.
Пусть y
1
––
один из корней этого уравнения. Тогда при y = y
1
условие
будет выполнено, так что имеет место
a
2
4
+ y
1
−b
x
2
+
ay
1
2
−c
x +
y
2
1
4
−d
= (kx + l)
2
при некоторых k и l. Исходное уравнение примет вид
x
2
+
a
2
x +
y
1
2
2
−
(
kx + l
)
2
= 0,
или
x
2
+
a
2
x +
y
1
2
+ kx + l
·
x
2
+
a
2
x +
y
1
2
−kx −l
= 0.
Приравняв к нулю каждый из сомножителей, находим четыре корня ис
-
ходного уравнения.
Пусть x
1
и x
2
––
корни первого сомножителя, x
3
и x
4
––
корни второго.
Тогда x
1
x
2
=
y
1
2
+ l, x
3
x
4
=
y
1
2
−l. Сложив эти равенства, получим, что
y
1
= x
1
x
2
+ x
3
x
4
. Таким образом, мы получим выражение корня y
1
вспо
-
могательного кубического уравнения через корни исходного уравнения
четвертой степени.
Другими корнями кубического уравнения будут
y
2
= x
2
x
3
+ x
1
x
4
, y
3
= x
2
x
4
+ x
1
x
3
.
Таким образом, мы нашли такое выражение y
1
= x
1
x
2
+ x
3
x
4
от корней x
1
,
x
2
, x
3
, x
4
, что при их всевозможных перестановках получается толь
-
ко два новых выражения. Поэтому эти выражения являются корнями
уравнения третьей степени, коэффициенты которого полиномиально вы
-
ражаются через коэффициенты исходного уравнения четвертой степени.
Данный результат можно было получить и двигаясь от этих выраже
-
ний к уравнению третьей степени.
Действительно, y
1
+ y
2
+ y
3
=
P
x
i
x
j
= b согласно теореме Виета для
уравнения x
4
+ ax
3
+ bx
2
+ cx + d = 0.

§ 4.9. Решение методом Лагранжа уравнений четвертой степени 243
Аналогично
y
1
y
2
+ y
2
y
3
+ y
3
y
1
= x
2
1
x
2
x
3
+ x
1
x
2
2
x
4
+ x
1
x
2
3
x
4
+ x
2
x
3
x
2
4
+ ... =
= (x
1
+ x
2
+ x
3
+ x
4
)(x
1
x
2
x
3
+ x
1
x
3
x
4
+ x
2
x
3
x
4
+ x
1
x
2
x
4
) −4x
1
x
2
x
3
x
4
=
= ac −4d
и также
y
1
y
2
y
3
= (x
3
1
x
2
x
3
x
4
+ x
1
x
3
2
x
3
x
4
+ x
1
x
2
x
3
3
x
4
+ x
1
x
2
x
3
x
3
4
) +
+ (x
2
1
x
2
2
x
2
3
+ x
2
1
x
2
2
x
2
4
+ x
2
1
x
2
3
x
2
4
+ x
2
2
x
2
3
x
2
4
) =
= x
1
x
2
x
3
x
4
(x
2
1
+ x
2
2
+ x
2
3
+ x
2
4
)
2
+ (x
1
x
2
x
3
+ x
1
x
2
x
4
+ x
1
x
2
x
3
+ x
2
x
3
x
4
)
2
−
−2(x
1
x
2
+ x
1
x
3
+ x
1
x
4
+ x
2
x
3
+ x
2
x
4
+ x
3
x
4
)x
1
x
2
x
3
x
4
=
= d(a
2
−2b) + (c
2
−2bd) = c
2
+ a
2
d −4bd.
Значит, y
1
, y
2
, y
3
––
корни уравнения
y
3
−by
2
+ (ca −4d)y − (c
2
+ a
2
d −4bd) = 0.
После решения этого уравнения остается справиться с системой
x
1
x
2
+ x
3
x
4
= y
1
;
x
1
x
3
+ x
2
x
4
= y
2
;
x
1
x
4
+ x
2
x
3
= y
3
.
Упражнение 109. Решите эту систему.
Рассмотрим еще один метод решения уравнения 4
-
й степени x
4
+
+ ax
2
+ bx + c = 0.
Возьмем другое выражение от корней x
1
, x
2
, x
3
, x
4
, которое тоже
принимает при переставлении корней всего 3 значения:
θ
1
= (x
1
+ x
2
)(x
3
+ x
4
), θ
2
= (x
1
+ x
3
)(x
2
+ x
4
), θ
3
= (x
1
+ x
4
)(x
2
+ x
3
).
Найдем кубическое уравнение с корнями θ
1
, θ
2
, θ
3
. Другими слова
-
ми, выразим его коэффициенты A = −θ
1
−θ
2
−θ
3
, B = θ
1
θ
2
+ θ
2
θ
3
+ θ
3
θ
1
,
C = −θ
1
θ
2
θ
3
через коэффициенты a, b, c:
θ
1
+ θ
2
+ θ
3
= 2(x
1
x
2
+ x
3
x
4
+ x
2
x
3
+ x
1
x
3
+ x
1
x
4
+ x
2
x
4
) = 2a,
θ
1
θ
2
+ θ
2
θ
3
+ θ
3
θ
1
= a
2
−4c, θ
1
θ
2
θ
3
= −b
2
.
Используя теорему Виета, имеем
(x −θ
1
)(x −θ
2
)(x − θ
3
) = x
3
−2ax
2
+ (a −4c)x + b
2
.
Найдя из этого уравнения θ
1
, θ
2
, θ
3
, можно определить и корни x
1
, x
2
,
x
3
, x
4
. Для этого используем равенство x
1
+ x
2
+ x
3
+ x
4
= 0, из которо
-
го следует, что (x
1
+ x
2
) = −(x
3
+ x
4
), (x
1
+ x
3
) = −(x
2
+ x
4
), (x
1
+ x
4
) =
= −(x
2
+ x
3
).
16*

244 Глава IV. Алгебраические уравнения
Значит,
x
1
+ x
2
=
p
−θ
1
; x
3
+ x
4
= −
p
−θ
1
;
x
1
+ x
3
=
p
−θ
2
; x
2
+ x
4
= −
p
−θ
2
;
x
1
+ x
4
=
p
−θ
3
; x
2
+ x
3
=
p
−θ
3
.
Отсюда можно выразить x
1
, x
2
, x
3
, x
4
.
Упражнение 110. Сделайте это.
Любопытно, что дискриминант найденного выше кубического уравне
-
ния равен дискриминанту уравнения 4
-
й степени для x. В самом деле,
θ
1
−θ
2
= −(x
1
−x
4
)(x
2
−x
3
);
θ
1
−θ
3
= −(x
1
−x
3
)(x
2
−x
4
);
θ
2
−θ
3
= −(x
1
−x
2
)(x
3
−x
4
).
Упражнение 111. Вычислите этот дискриминант.
Задачи и упражнения к § 4.9
1. Решите биквадратное уравнение методом Лагранжа.
2. Решите уравнения:
а) x
4
−2(a
2
+ b
2
)x
2
+ (a
2
−b
2
)
2
= 0;
б) x
4
−a(a + b)x
2
+ a
3
b = 0;
в) (x
2
+ 1)
2
= 4(2x − 1);
г) (x
2
−16)(x −3)
2
+ 9x
2
= 0;
д) x
4
−12x + 323 = 0;
е) (6x + 5)
2
(3x + 2) (x + 1) = 35;
ж) x
4
+ x
3
+ x + 1 = 4x
2
;
з) (1 + x)
4
= 2(1 + x)
4
;
и) 45(x
2
+ x + 1)
2
= 49(x + 1)
2
(x + 1)
2
;
к) (x
2
−10x + 15) (x
2
−8x + 15) = 3(x
2
−6x + 15)x.
3. Составить уравнение 4
-
й степени с корнями α, 1
/
α, −α, −1
/
α.
4. Пусть a и b
––
два из четырех корней многочлена x
4
+ x
3
−1. До
-
кажите, что ab
––
корень многочлена x
6
+ x
4
+ x
3
−x
2
−1.
§ 4.10. Решение методом Эйлера уравнений
четвертой степени
Существуют и другие способы решения уравнения четвертой степени.
Один из наиболее изящных принадлежит Эйлеру. Этот способ состоит
в следующем.

§ 4.10. Решение методом Эйлера уравнений четвертой степени 245
Полное уравнение четвертой степени
y
4
+ Ay
3
+ By
2
+ Cy + D = 0 (5)
подстановкой y = x −
A
4
приводится к более простому виду:
x
4
+ ax
2
+ bx + c = 0. (6)
Полагаем:
2x = u + v + w. (7)
В равенство (7) введено три неизвестных. Чтобы определить их, нужно
будет дать три уравнения.
Возводя обе части равенства (7) два раза в квадрат, получаем:
4x
2
= u
2
+ v
2
+ w
2
+ 2(uv + uw + vw),
16x
4
= (u
2
+ v
2
+ w
2
)
2
+ 4(uv + uw + vw) (u
2
+ v
2
+ w
2
) +
+ 4(u
2
v
2
+ u
2
w
2
+ v
2
w
2
) + 8uvw(u + v + w). (8)
Подставляя в уравнение (6) вместо x, x
2
и x
4
их выражения из ра
-
венств (7) и (8), после упрощения получим:
(u
2
+ v
2
+ w
2
)
2
+ 4(uv + uw + vw) (u
2
+ v
2
+ w
2
+ 2a) +
+ 4a(u
2
+ v
2
+ w
2
) + 8(uvw + b) (u + v + w) +
+ 4(u
2
v
2
+ u
2
w
2
+ v
2
w
2
) + 16c = 0. (9)
Для того чтобы выполнялось равенство 2x = u + v + w, где x
––
корень
уравнения (6), необходимо и достаточно выполнение уравнения (9). Оно
содержит три неизвестных. Чтобы определить их, нужны еще два урав
-
нения, которые можно выбрать произвольно. Свободой выбора следует
воспользоваться для наибольшего упрощения уравнения.
Руководствуясь этим, положим
u
2
+ v
2
+ w
2
= −2a; uvw = −b. (10)
При этом выборе величин u, v и w уравнение (9) обращается в уравнение
u
2
v
2
+ u
2
w
2
+ v
2
w
2
= a −4c. (11)
Из (10) и (11) заключаем, что u, v и w удовлетворяют системе уравнений
u
2
+ v
2
+ w
2
= −2a;
u
2
v
2
+ u
2
w
2
+ v
2
w
2
= a
2
−4c;
u
2
v
2
w
2
= b
2
.
(12)

246 Глава IV. Алгебраические уравнения
Отсюда следует, что числа u
2
, v
2
и w
2
являются корнями уравнения:
σ
3
+ 2aσ
2
+ (a
2
−4c) −b
2
= 0. (13)
Оно совпадает с резольвентой Феррари, полученной ранее.
Пусть σ
1
, σ
2
, σ
3
––
корни резольвенты. Положим u
2
= σ
1
, v
2
= σ
2
,
w
2
= σ
3
. Извлекая корни, имеем
u = ±
√
σ
1
, v = ±
√
σ
2
, w = ±
√
σ
3
. (14)
При этом, в силу равенства (10), выполняется равенство
(±
√
σ
1
) · (±
√
σ
2
) · (±
√
σ
3
) = −b. (15)
У двух радикалов в равенствах (14) можно взять любое из их значений.
После этого значение третьего радикала следует взять определенное
––
оно находится из равенства (15).
Подставляя полученные выражения для u, v, w в уравнение (7), при
-
ходим к следующей теореме.
Теорема 100 (Эйлер). Корни приведенного уравнения четвер-
той степени
x
4
+ ax
2
+ bx + c = 0
выражаются через корни резольвенты Феррари
σ
3
+ 2aσ
2
+ (a
2
−4c)σ − b
2
= 0
по формулам:
2x
1
=
√
σ
1
+
√
σ
2
+
√
σ
3
; 2x
2
=
√
σ
1
−
√
σ
2
−
√
σ
3
;
2x
3
= −
√
σ
1
+
√
σ
2
−
√
σ
3
; 2x
4
= −
√
σ
1
−
√
σ
2
+
√
σ
3
.
При этом значения радикалов
√
σ
1
,
√
σ
2
и
√
σ
3
должны быть вы-
браны так, чтобы выполнялось равенство:
√
σ
1
·
√
σ
2
·
√
σ
3
= −b.
Задачи и упражнения к § 4.10
1. Решите биквадратное уравнение методом Эйлера.
2. Решите уравнения:
а) x
4
+ 2x +
3
2
= 0;
б) x
4
−
17
2
x
2
+ 10x −
31
16
= 0;
в) x
4
−12x
2
−24x −14 = 0.

§ 4.11. Основная теорема алгебры 247
3. Разложите на множители над полем действительных чисел
а) (x
2
+ x + 4)
2
+ 8x(x
2
+ x + 4)
2
+ 15x;
б) (x + 1) (x + 3) (x + 5) (x + 7) + 15;
в) 4(x + 5) (x + 6) (x + 10) (x + 12) −3x
2
;
г) x
4
+ 4;
д) x
4
+ 4x
2
+ 4x + 1.
§ 4.11. Основная теорема алгебры
Важным шагом в развитии теории алгебраических уравнений стало
использование комплексных чисел в качестве коэффициентов уравнений.
В 1799 г. Гаусс дал первое строгое доказательство существования ком
-
плексных решений для любого алгебраического уравнения (этот факт был
известен и ранее и был доказан Даламбером *, правда, с некоторым про
-
белом).
Теорема 101 (Даламбер
––
Гаусс). Всякий многочлен степени
n > 1 имеет комплексный корень.
Д о к а з а т е л ь с т в о. Для понимания идеи одного из самых на
-
глядных доказательств этой теоремы можно предложить следующие
неформальные рассуждения. Это доказательство, носящее название
«
Дама с собачкой
»
, рассказывалось А. Н. Колмогоровым в 1930
-
е годы
на лекции для школьников в МГУ.
Рассмотрим многочлен f(z) = z
n
+ a
1
z
n−1
+ ... + a
n
с комплексными
коэффициентами и a
n
6= 0. Заметим, что все его корни (если они суще
-
ствуют) лежат в круге радиуса R = n ·max
i
|a
i
|. Действительно, при |z|> R
|z
n
|> |a
1
z
n−1
+ ... + a
n
|,
и поэтому f(z) 6= 0. В тоже время при малых по модулю z значение f(z)
близко к a
n
.
Представим f(z) в виде суммы двух частей z
n
и g(z) = a
1
z
n−1
+ ...
... + a
n
, которые назовем соответственно
«
дамой
»
и
«
собачкой
»
. Рас
-
смотрим образы окружностей различных радиусов c центрами в точке O
при отображении f(z) (рис. 34).
Для радиуса R при движении по окружности
{R(cos ϕ + i sin ϕ) : 0 6 ϕ 6 2π}
* Ж. Л. Даламбер (Jean Le Rond d’Alembert, 1717
–
1783)
––
выдающийся французский
математик и механик, один из организаторов издания знаменитой
«
Энциклопедии
»
.
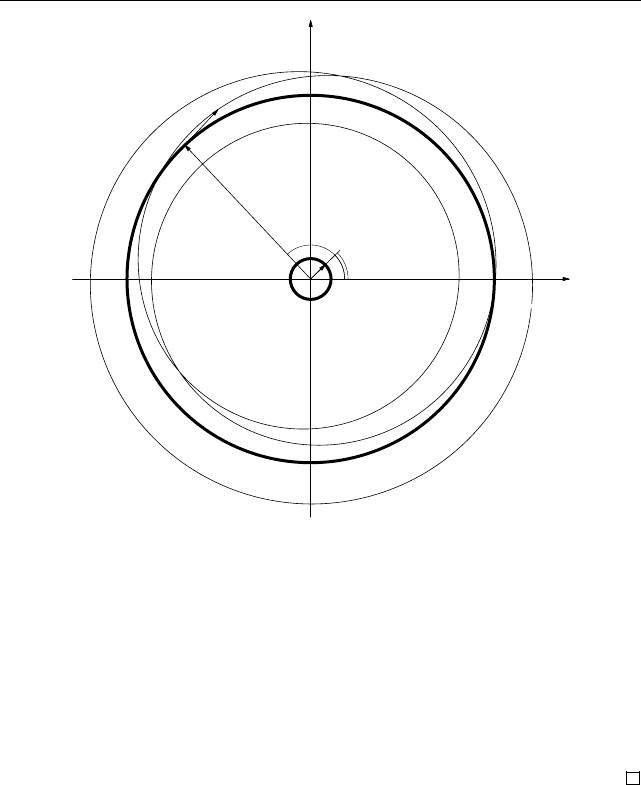
248 Глава IV. Алгебраические уравнения
α
nα
z
z
n
g (n)
y
x
R
R
n
Рис. 34
дама будет двигаться в образе со скоростью, в n раз большей, по окруж
-
ности радиуса R
n
. Собачка g(z) = f(z) −z
n
будет мала по модулю и не за
-
денет за точку (0, 0), как было показано выше. При малых радиусах образ
будет
«
бегать
»
неподалеку от точки a
n
6= 0.
Начнем непрерывно уменьшать радиус окружности от R до 0. В начале
точка (0, 0) была внутри, а в конце стала находиться вне множества,
ограниченного образом окружности. В силу непрерывности будет момент
прохождения через эту точку. Это означает, что в этот момент f(z) = 0,
т. е. у многочлена f(z) есть комплексный корень.
Следующие теоремы являются следствиями основной теоремы ал
-
гебры.
Теорема 102 (о разложении на линейные множители). Всякий
многочлен f(x) ∈C [x], deg f(x) = n > 1, над полем комплексных чисел
раскладывается в произведение n линейных множителей.
Д о к а з а т е л ь с т в о. Индукция по n. При n = 1 многочлен яв
-
ляется линейным. Предположим, что утверждение уже доказано для
многочленов степени n, и пусть f(x)
––
многочлен степени n + 1. Тогда

§ 4.11. Основная теорема алгебры 249
f(x) имеет некоторый корень α
1
∈C, и по теореме Безу f(x) представ
-
ляется в виде f(x) = (x − α
1
) f
1
(x). Но многочлен f
1
(x) имеет степень n,
и по предположению индукции раскладывается в произведение n линей
-
ных множителей. Но тогда f(x) является произведением n + 1 линейного
множителя.
Теорема 103 (о числе корней). Всякий многочлен степени n > 1
с комплексными коэффициентами имеет n корней, если считать
каждый корень столько раз, какова его кратность.
Д о к а з а т е л ь с т в о. Как мы только что доказали, многочлен сте
-
пени n > 1 раскладывается в произведение n линейных множителей:
f(x) = a
0
(x −α
1
)(x −α
2
) ... (x −α
n
). Ясно, что α
1
, ..., α
n
––
это корни
многочлена f(x).
Объединяя равные сомножители в степени, f(x) можно представить
в виде
f(x) = a
0
(x −α
1
)
k
1
(x −α
2
)
k
2
... (x − α
s
)
k
s
,
где корни α
1
, . . ., α
s
уже все различны, а показатели k
1
, . .., k
s
––
это крат
-
ности этих корней.
Поскольку степени многочленов в левой и правой частях этого равен
-
ства одинаковы, то n = k
1
+ k
2
+ ... + k
s
.
Упражнение 112. Многочлен f(x) делится на многочлен g(x) тогда
и только тогда, когда всякий корень f(x) является корнем g(x) и крат
-
ность его в g(x) не больше кратности в f(x).
У к а з а н и е. Используйте разложение многочленов f(x) и g(x)
на линейные множители.
Теорема 104 (Виет). Пусть
f(x) = a
0
x
n
+ a
1
x
n−1
+ ... + a
n−1
x + a
n
, a
0
6= 0,
––
многочлен с комплексными коэффициентами. Тогда для любо-
го k = 1, .. ., n сумма всевозможных произведений корней многочле-
на f(x), состоящих из k сомножителей, равна (−1)
k
a
k
/
a
0
. В част-
ности, сумма всех корней многочлена f(x) равна −a
1
/
a
0
, сумма по-
парных произведений равна a
2
/
a
0
, произведение всех корней равно
(−1)
n
a
n
/
a
0
.
Д о к а з а т е л ь с т в о. Представим f(x) в виде:
f(x) = a
0
(x −α
1
)(x −α
2
) ... (x −α
n
).
250 Глава IV. Алгебраические уравнения
Тогда после раскрытия скобок в правой части имеем:
a
0
x
n
+ a
1
x
n−1
+ ... + a
n
=
= a
0
x
n
−a
0
(α
1
+ ... + α
n
)x
n−1
+ ... + (−1)
n
a
0
α
1
α
2
... α
n
.
Если два многочлена равны, то равны их коэффициенты. Поэтому
−a
0
(α
1
+ ... + α
n
) = a
1
, .. ., (−1)
n
a
0
α
1
... α
n
= a
n
.
Теорема 105 (о разложении действительных многочленов). Вся-
кий многочлен степени n > 1 с действительными коэффициентами
раскладывается в произведение линейных двучленов и квадратных
трехчленов с отрицательными дискриминантами, имеющими дей-
ствительные коэффициенты.
Д о к а з а т е л ь с т в о. Индукция по n. Для многочленов степени 1
и 2 утверждение верно. Предположим, что оно справедливо для любых
многочленов степени, не большей n, и пусть f(x) имеет степень n + 1.
Многочлен f(x) имеет комплексный корень α. По теореме Безу
f(x) = (x −α) g(x), (16)
и если число α действительное, то g(x)
––
многочлен с действительными
коэффициентами. Тогда по предположению индукции g(x) раскладыва
-
ется в произведение требуемого вида. Но тогда в силу (16) такое разло
-
жение существует и для многочлена f(x).
Пусть теперь α
––
число не действительное, т. е. ¯α 6= α. По следствию
из теоремы 93 число ¯α также является корнем многочлена f(x). Тогда
из (16) при x = ¯α получаем, что f( ¯α) = ( ¯α −α) g( ¯α), и, следовательно,
g( ¯α) = 0. Снова применяя теорему Безу, имеем g(x) = (x − ¯α)h(x), а тогда
из (16) следует, что
f(x) = (x − α) (x − ¯α)h(x) = (x
2
− (α + ¯α)x + α ¯α)h(x). (17)
Так как α + ¯α и α ¯α
––
числа действительные, то трехчлен x
2
− (α + ¯α)x +
+ α ¯α имеет действительные коэффициенты (и, очевидно, отрицательный
дискриминант), значит, и многочлен h(x) имеет действительные коэффи
-
циенты как частное двух многочленов с действительными коэффициен
-
тами.
Но многочлен h(x) имеет степень меньше n, так что к нему приме
-
нимо предположение индукции. После этого требуемое утверждение для
многочлена f(x) вытекает из равенства (17).
Приведем примеры применения доказанных теорем при решении
задач.
