Гашков С.Б. Современная элементарная алгебра в задачах и решениях
Подождите немного. Документ загружается.


§ 4.3. Комплексные числа 211
П р и м е р ы. 1. (3 + 4i)
−1
=
3
25
−
4
25
i.
2. (1 + i)
−1
=
1
2
−
1
2
i.
Определение 94. Обозначим через |z| неотрицательное действитель
-
ное число
p
Re z
2
+ Im z
2
=
p
a
2
+ b
2
,
называемое модулем комплексного числа z. Через
z обозначим ком
-
плексное число Re z − i Im z = a −ib, называемое сопряженным к z
комплексным числом.
П р и м е р ы. 1. |3 + 4i|=
√
3
2
+ 4
2
= 5.
2. 3 + 4i = 3 −4i.
Упражнение 85. Проверьте, что
z
−1
=
¯
z
|z|
2
, |
¯
z| = |z|, z +
¯
z = 2a, |z
−1
|=
1
|z|
, |z|
2
= z ·
¯
z.
Проверьте, что уравнение z
2
w = z
1
с комплексной неизвестной w при
z
2
6= 0 имеет единственное решение w = z
1
·z
−1
2
. Найдите это решение
непосредственно.
Определение 95. Число z
1
·z
−1
2
называется частным чисел z
1
, z
2
и обозначается
z
1
z
2
.
П р и м е р ы. 1.
1
(3 −4i)
=
3
25
+
4
25
i.
2.
(3 + 4i)
(3 −4i)
= (3 + 4i)
3
25
+
4
25
i
= −
7
25
+
24
25
i.
3. Если |z| = 1, то
1
z
=
¯
z.
4. Иногда деление комплексных чисел можно выполнить быстрее, чем
пользуясь непосредственным определением:
8 −27i
2 + 3i
=
2
3
+ 3
3
i
2 + 3i
= 2
2
−6i −9 = −5 −6i.
Далее множество всех комплексных чисел обозначается C.
Упражнение 86. Проверьте, что для любых z, w ∈C
z ±w = z ± w, zw = z · w, z
/
w = z
/
w,
где в последнем тождестве, естественно, w 6= 0.
На алгебраическом жаргоне предыдущее утверждение сформулирова
-
ли бы так: операция сопряжения является автоморфизмом поля C.
14*
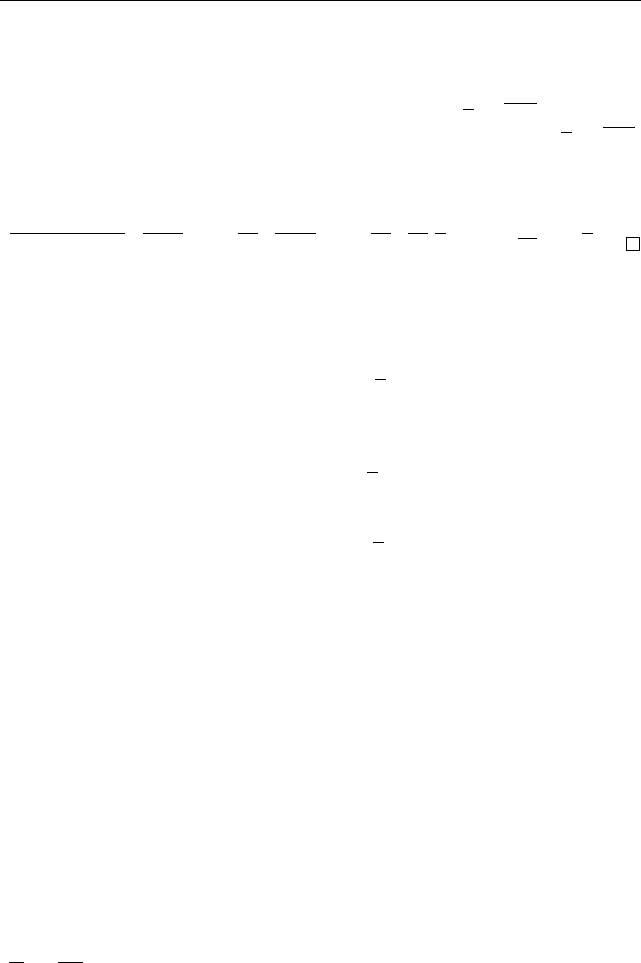
212 Глава IV. Алгебраические уравнения
Это утверждение обобщается в следующей теореме.
Теорема 93. Пусть f(z)
––
произвольный многочлен с комплексны-
ми коэффициентами, а многочлен f
∗
(z) получается из него заменой
всех коэффициентов на сопряженные. Тогда f
∗
(
z) = f(z) и, в част-
ности, если все коэффициенты f(z) действительные, то f(
z) = f(z).
Д о к а з а т е л ь с т в о. Пусть f(z) = a
n
z
n
+ ... + a
0
, тогда, применяя
индукцию и тождества упражнения 86, имеем
a
n
z
n
+. ..+a
0
=a
n
z
n
+. ..+a
0
=a
n
z
n
+. ..+a
0
=a
n
(z)
n
+. . .+a
0
= f
∗
(z).
Следствие из теоремы 93. Пусть f(z)
––
произвольный многочлен
с комплексными коэффициентами, а многочлен f
∗
(z) получается
из него заменой всех коэффициентов на сопряженные. Тогда
f
∗
(z) = 0 ⇔ f(
z) = 0
и, в частности, если все коэффициенты f(z) действительные, то
f(z) = 0 ⇔ f(
z) = 0.
Определение 96. Скалярным произведением чисел z = a + ib
и w = c + id назовем число hw, zi= Re (w
z) = ac + bd.
Упражнение 87. Проверьте следующие свойства скалярного произ
-
ведения:
а) симметричность: hw, zi= h z, wi;
б) однородность: ahw, zi= haw, zi для любого a ∈R;
в) аддитивность hw
1
+ w
2
, zi= hw
1
, zi+ hw
2
, zi;
г) неотрицательность квадрата (положительная определенность)
hz, zi = |z|
2
> 0.
Определение 97. Числа z и w назовем ортогональными, если
hw, zi = 0.
Упражнение 88. Проверьте, что
а) числа z и iz всегда ортогональны,
б) числа z и w ортогональны ⇔ z = iaw, где a ∈R.
Упражнение 89. Выведите из упражнения 86, что модули ком
-
плексных чисел удовлетворяют следующим тождествам: |zw|= |z|·|w|,
z
w
=
|z|
|w|
.

§ 4.3. Комплексные числа 213
Упражнение 90. а) Запишите первое из двух предыдущих тождеств,
заменяя модули их выражениями через действительные и мнимые части.
Полученное тождество называется тождеством Фибоначчи и было от
-
крыто задолго до появления комплексных чисел.
б) Докажите его непосредственно.
в) Натуральное число назовем шумерским, если оно является суммой
двух квадратов натуральных чисел. Докажите, что произведение шумер
-
ских чисел
––
шумерское число.
г) Проверьте тождество hw, zi
2
+ hiw, zi
2
= |z|
2
|w|
2
. У к а з а
-
н и е. Так как Re (iz) =−Im z, то hiw, zi = Re (iw
z) = − Im (wz), значит,
hw, zi
2
+ hiw, zi
2
= Re (w
z)
2
+ Im (wz)
2
= |wz|
2
= |z|
2
|w|
2
.
д) Проверьте, что предыдущее тождество
––
это просто другая запись
тождества Фибоначчи.
Из тождества Фибоначчи немедленно следует частный случай нера
-
венства Коши
––
Буняковского
––
Шварца |hw, zi|6 |z|·|w|.
Упражнение 91. Проверьте, что в равенство оно обращается тогда
и только тогда, когда z = aw, где a ∈R.
Из неравенства |hw, zi|6 |z|·|w| немедленно следует неравенство
треугольника |z|+ |w|> |z + w|. Действительно, согласно упражне
-
нию 87 и неравенству Коши
––
Буняковского
|z + w|
2
= hw + z, w + zi= hw, wi+ hz, zi + 2hw, zi6
6 |w|
2
+ |z|
2
+ 2|z||w|= (|z|+ |w|)
2
.
Для комплексных чисел есть удобная геометрическая интерпрета
-
ция *
––
их изображают точками плоскости с координатами (a, b).
*
z(a, b)
Re z
• •
•
Im z
-
6
Рис. 24
Эквивалентным образом, их можно изоб
-
ражать векторами, выходящими из начала
координат и с концом в точке (a, b) (рис. 24).
Множество всех действительных чисел при
этом изображается одной из осей координат,
называемой действительной осью, а мно
-
жество всех чисто мнимых чисел, т.е. чисел
с нулевой действительной частью, изображается другой осью координат,
называемой мнимой осью. Модулем комплексного числа является длина
изображающего его вектора.
* Предложенная в начале XIX в. независимо французом Ж. Арганом и датчанином
К. Весселем, но вошедшая во всеобщее употребление благодаря Гауссу.

214 Глава IV. Алгебраические уравнения
H
H
H
H
H
H
H
H
•
•
z(2, 1)
¯
z (2, −1)
-
6
Рис. 25. Операция
сопряжения
Очевидно, например, что на комплексной
плоскости числа z и
¯
z расположены симметрич
-
но относительно действительной оси (рис. 25).
Операция сложения комплексных чисел ин
-
терпретируется как сложение векторов (рис. 26).
Определение 98. Угол ϕ, образованный
вектором z и положительным направлением
действительной оси Ox, называется аргумен-
том комплексного числа z и обозначается arg z.
Аргумент определяется только для нену
-
левых чисел и обычно берется в пределах
0 6 arg z < 2π.
*
•
z
1
(2, 1)
•
•
z
2
(1, 1)
3
*
z(3, 2) = z
1
+ z
2
-
6
Рис. 26. Сложение комплексных
чисел
(a, b)
|z|
-
6
•
ϕ
a
b
Рис. 27. Тригонометрическая
форма
П р и м е р ы. 1. arg(1 + i) = π
/
4. 2. arg(1 −i) = 7π
/
4. 3. arg(−1 −i) =
= 5π
/
4. 4. arg(−1 + i) = 3π
/
4.
Из треугольника, изображенного на рис. 27, легко выразить тригоно
-
метрические функции от аргумента ϕ:
cos ϕ =
a
p
a
2
+ b
2
, sin ϕ =
b
p
a
2
+ b
2
, tg ϕ =
b
a
.
Отсюда
a =
p
a
2
+ b
2
cos ϕ = |z| cos ϕ,
b =
p
a
2
+ b
2
sin ϕ = |z| sin ϕ,
значит,
z = a + bi = |z|(cos ϕ + i sin ϕ).
Получившаяся (так называемая тригонометрическая) форма записи чис
-
ла z удобна при умножении.
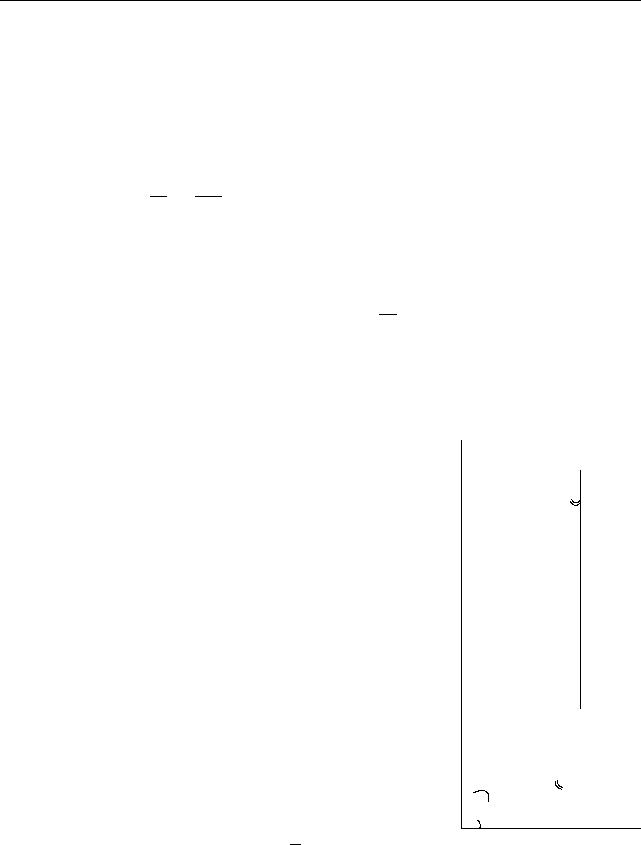
§ 4.3. Комплексные числа 215
Упражнение 92. Используя тригонометрические теоремы сложения,
проверьте, что если
z
1
= |z
1
|(cos ϕ
1
+ i ·sin ϕ
1
), z
2
= |z
2
|(cos ϕ
2
+ i ·sin ϕ
2
),
то
z
1
·z
2
= |z
1
·z
2
|(cos(ϕ
1
+ ϕ
2
) + i sin(ϕ
1
+ ϕ
2
)),
z
1
z
2
=
|z
1
|
|z
2
|
(cos(ϕ
1
−ϕ
2
) + i sin(ϕ
1
−ϕ
2
)).
В последнем равенстве предполагается, конечно, что z
2
6= 0.
Упражнение 93. Из предыдущих равенств выведите, что
arg
(
z
1
z
2
)
= (arg z
1
+ arg z
2
) mod 2π, arg
z
1
z
2
= (arg z
1
−arg z
2
) mod 2π.
Применяя индукцию, докажите, что
arg(z
1
z
2
... z
n
) = (arg z
1
+ arg z
2
+ ... + arg z
n
) mod 2π.
z
2
(2, 2)
•
*
z
1
(2, 1)
•
z(2, 6) = z
1
z
2
•
-
1
-
6
ϕ
ϕ
ψ
ψ
Рис. 28. Умножение
комплексных чисел
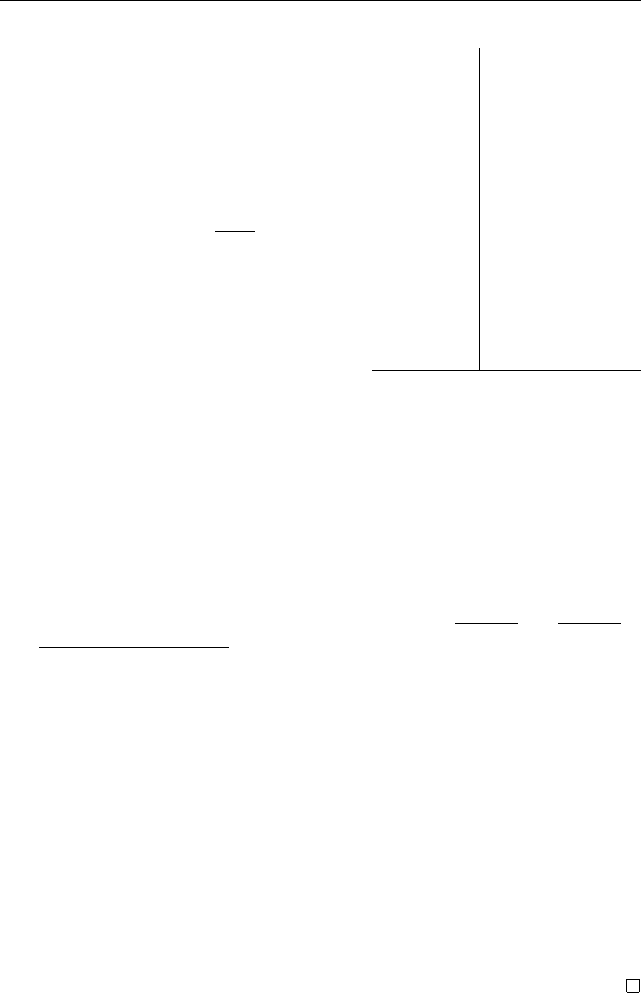
Упражнение 94. Докажите, что при умноже
-
нии чисел z
i
всегда на диаграмме Весселя
––
Аргана
(рис. 28) треугольники с вершинами в точках (0, 0),
(1, 0), z
1
и (0, 0), z
2
, z подобны.
Упражнение 95. Постройте циркулем и ли
-
нейкой сумму, разность, произведение и частное
двух данных комплексных чисел (единица масшта
-
ба, действительная и мнимая оси заданы). Попро
-
буйте сделать это самым экономным образом.
Скалярное произведение чисел z и w теперь,
оказывается, совпадает со скалярным произве
-
дением векторов z и w, которое геометрически
определяется как произведение длин векторов на
косинус угла между ними.
Упражнение 96. Проверьте, что действитель
-
но для ненулевых векторов
|z||w| cos arg(w
/
z) = Re (w
z) = hw, zi.
Теперь мы можем использовать комплексные
числа для доказательства геометрических тео
-
рем. Например, теорему о высотах треугольни
-
ка можно доказать следующим образом. Пусть дан треугольник ABC
(см. рис. 29). Выберем систему координат так, чтобы основание AB
216 Глава IV. Алгебраические уравнения
a
P
P
P
P
P
P
P
P
P
O
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
−iab
/
c
ic
ic
b
Рис. 29. Теорема об ортоцентре
лежало на действительной оси, а мни
-
мая ось проходила по высоте CO, где O
совпадает с началом координат. Тогда
вершины треугольника A, B изобража
-
ются действительными числами a, b,
а вершина C
––
чисто мнимым числом ic.
Тогда ортоцентру H (точке пересече
-
ния высот) треугольника ABC отвеча
-
ет чисто мнимое число
−iab
c
. Действи
-
тельно, вектор AH соответствует числу
a + (iab)
/
c, а вектор BC
––
числу b −ic,
а согласно упражнению 88 эти век
-
тора ортогональны (перпендикулярны),
так как a + (iab)
/
c = (b − ic)ia
/
c, ана
-
логично BH ортогонален AC, так как
b + (iab)
/
c = (a −ic)ib
/
c, а ортогональ
-
ность OH и AB ясна из условия.
Неравенства |z
1
|−|z
2
|6 |z
1
±z
2
|6 |z
1
|+ |z
2
| можно интерпретиро
-
вать на комплексной плоскости как неравенства треугольника. Первое
из них уже было доказано. Второе неравенство следует из первого при
смене знака у z
2
.
Упражнение 97. а) Найдите условие обращения неравенства тре
-
угольника в равенство с помощью комплексных чисел.
б) Докажите неравенство |z
1
+ z
2
|6 |z
1
|+ |z
2
| с использованием
действительных чисел, сведя его к неравенству
√
x
2
1
+ y
2
1
+
√
x
2
2
+ y
2
2
>
>
p
(x
1
+ x
2
)
2
+ (y
1
+ y
2
)
2
.
в) Докажите неравенство |z
1
±... ±z
n
|6 |z
1
|+ ... + |z
n
|.
С помощью тригонометрической формы доказывается следующая те
-
орема.
Теорема 94 (формула Муавра). Если z = r (cos α + i sin α), то при
любом натуральном n
z
n
= r
n
(cos nα + i sin nα).
Д о к а з а т е л ь с т в о. Доказательство проводится по индукции. Ба
-
за индукции (n = 1) очевидна. Шаг индукции обосновывается с помощью
упражнения 92. Легко видеть, что формула Муавра верна и для отрица
-
тельных целых n.
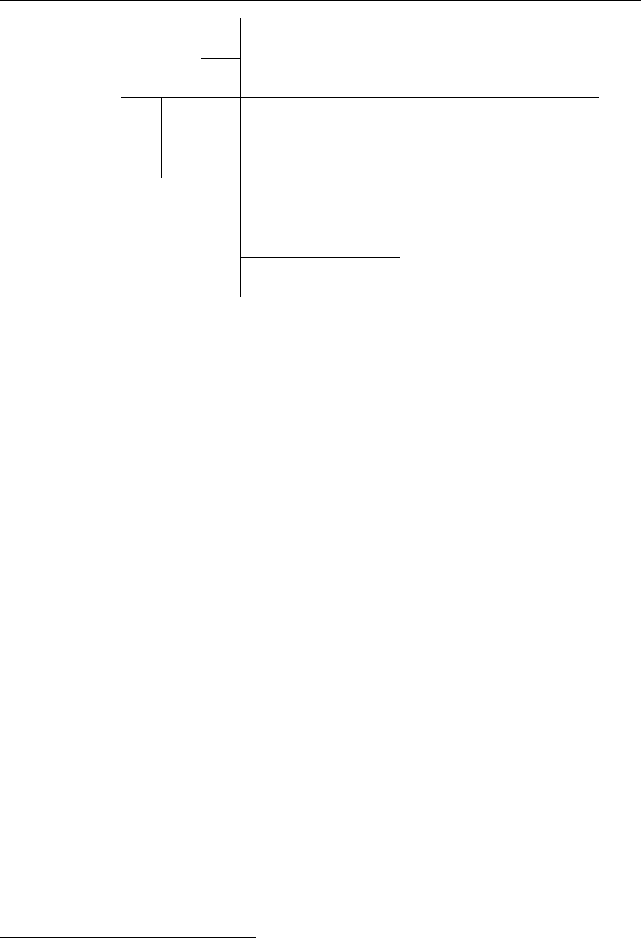
§ 4.3. Комплексные числа 217
z(1, 1)
@
6
6
z
2
(2, 0)
@
@I
z
3
(−2, 2)
z
4
(−4, 0)
z
5
(−4, −4)
?
z
6
(0, −8)
@
@
@
@
@
@
@
@
@
@
@
@R
z
7
(8, −8)
-
z
8
(16, 0)
-
Рис. 30. Возведение в степень комплексных чисел
На рис. 30 видно, что точки w
n
укладываются на спиральную линию,
состоящую из точек w, удовлетворяющих условию
|w| = c
arg w
.
Упражнение 98. Найдите эту константу c, соответствующую изоб
-
раженным числам.
Свойство этой спирали не изменяться при преобразованиях подобия
так потрясло Якоба Бернулли *, что согласно завещанию ее изобразили
на его могильной плите в Базельском соборе с надписью
«
Eadem mutata
resurgo
»
**. Кроме Бернулли, ее изучали ранее Декарт и Торичелли. Лю
-
бопытно, что логарифмическая спираль используется в технике и даже
встречается в живой природе (ее можно увидеть на раковине моллюс
-
ка Haliotis splendis, а также внимательно разглядывая расположение
семечек в подсолнухе).
Задачи и упражнения к § 4.3
1. Вычислите (29 + 23i)
/
(1 + 5i).
2. Докажите, что:
а) точки 1 + 4i, 2 + 7i, 3 + 10i лежат на одной прямой;
б) точки 2 + i, 4 + 4i, 6 + 9i, 8 + 16i лежат на одной параболе.
* Я. Бернулли (Jacob Bernoulli, 1654
–
1705)
––
знаменитый швейцарский математик.
Брат не менее знаменитого Иоганна Бернулли.
** Измененная, воскресаю прежней (лат.).

218 Глава IV. Алгебраические уравнения
3. Докажите неравенство треугольника с помощью тригонометриче
-
ской формы.
У к а з а н и е. Пусть z
1
=r
1
(cos ϕ
1
+i sin ϕ
1
), z
2
=r
2
(cos ϕ
2
+i sin ϕ
2
),
тогда z
1
+ z
2
= r
1
cos ϕ
1
+ r
2
cos ϕ
2
+ i(r
1
sin ϕ
1
+ r
2
sin ϕ
2
), откуда
|z
1
+ z
2
|
2
= (r
1
cos ϕ
1
+ r
2
cos ϕ
2
)
2
+ (r
1
sin ϕ
1
+ r
2
sin ϕ
2
)
2
=
= r
2
1
+ 2r
1
r
2
cos(ϕ
1
−ϕ
2
) + r
2
2
6 (r
1
+ r
2
)
2
= (|z
1
|+ |z
2
|)
2
.
4. Какие части комплексной плоскости C выделяются условиями:
Re z > 0, Re z > 0, Re z = 0, a 6 Im z 6 b, |z −z
0
|= R, |z −z
0
|< R,
R 6 |z|6 R
′
, Re 1
/
z = 1
/
R?
5. Найдите множество точек на комплексной плоскости C, удовле
-
творяющее условиям:
а) |z −a|+ |z −b| = k (эллипс);
б) |z − a|+ |z − b|6 k;
в) |z −a|−|z −b|= k (гипербола);
г) |z − a|
/
|z −b|= k (окружность Аполлония);
д) |z − a|
/
|1 −
¯
az|< 1;
е) |z − a|
/
|1 −
¯
az| > 1.
6. Отображение комплексной плоскости C в себя, задаваемое фор
-
мулой w = iz, есть поворот вокруг начала координат на угол 90
◦
.
7. Отображение комплексной плоскости C в себя, задаваемое фор
-
мулой w = az, |a|= 1, есть поворот вокруг начала координат.
8. Отображение комплексной плоскости C в себя, задаваемое фор
-
мулой w = az + b, a, b ∈C, есть подобие первого рода (не меняющее
ориентации), при |a|= 1
––
движение (т. е. преобразование, не меняющее
расстояния между точками), при a = 1
––
параллельный перенос.
9*. Отображение комплексной плоскости в себя, задаваемое фор
-
мулой w = 1
/
¯
z, есть инверсия с центром в 0 относительно окружности
|z| = 1.
10. Найдите максимум и минимум |z| при условии
z +
1
z
= a.
11. Отображение C в C, задаваемое формулой
w =
az + b
cz + d
, a, b, c, d ∈C, ad − bc 6= 0,
переводит прямую и окружность в прямую или окружность и сохраняет
углы между ними.
12. Если точки z
k
лежат на одной прямой, то (z
1
−z
2
)
/
(z
2
−z
3
) ∈R,
и обратно.

§ 4.3. Комплексные числа 219
13. Если точки z
k
лежат на одной окружности, то
(z
1
−z
3
)
/
(z
2
−z
3
)
/
(z
1
−z
4
)
/
(z
2
−z
4
)
∈R,
и обратно.
14*. Найдите наибольшее натуральное n такое, что существуют числа
z
1
, ..., z
n
∈C, для которых min
i6= j
|z
i
−z
j
|> max
i
|z
i
|. Найдите эти числа.
15. Если стороны треугольника удовлетворяют равенству
a
2
+ b
2
+ c
2
= ab + bc + ac,
то треугольник правильный.
16. Если вершинами треугольника на комплексной плоскости явля
-
ются числа u, v, w, удовлетворяющие равенству
u
2
+ v
2
+ w
2
= uv + vw + uw,
то треугольник правильный.
17. Если вершинами треугольника на комплексной плоскости явля
-
ются числа u, v, w, то его центр тяжести (точка пересечения медиан)
изображается числом (u + v + w)
/
3.
H
H
H
H
A
C
B
D
Рис. 31. Теорема
Птолемея
18. Докажите неравенство Птолемея: для лю
-
бого четырехугольника ABCD
|AD||BC|6 |BD||AC|+ |CD||AB|.
У к а з а н и е. Примените тождество для комплекс
-
ных чисел
(a −d) (c − b) + (b −d) (a −c) + (c − d)(b −a) = 0
и выведите из него с помощью неравенства тре
-
угольника, что
|a −d||b − c| 6 |b −d||a −c|+ |c − d||a −b|.
19. Докажите, что для четырехугольника ABCD равенство
|AD||BC|= |BD||AC|+ |CD||AB|
справедливо тогда и только тогда, когда вокруг него можно описать
окружность.
У к а з а н и е. Примените указание к задаче 18 и задачу 13.
20. Докажите тождества и предложите для них геометрическую ин
-
терпретацию:
а) |z + w|
2
+ |z −w|
2
= 2(|z|
2
+ |w|
2
),
б) |z|+ |w|= |(z + w)
/
2 −
√
zw|+ |(z + w)
/
2 +
√
zw|.
У к а з а н и е.
√
a = b, если b
2
= a.

220 Глава IV. Алгебраические уравнения
21. Докажите, что отображение w = (1 + iz)
/
(1 −iz) переводит полу
-
плоскость Im z > 0 в круг |w|6 1.
22. Пусть |z|= |u|= |w|. Докажите, что
zu + uw + zw
z + u + w
= |z|.
Докажите, что при условии |z|= |u|= |w| следующие утверждения экви
-
валентны:
а) точки z, u, w образуют правильный треугольник, т. е. |z − w| =
= |z −u|= |u −w|,
б) справедливо равенство z + u + w = 0,
в) числа z, u, w являются корнями уравнения вида x
3
= v, v ∈C.
23. Пусть |z
1
|= |z
2
|= |z
3
|= |z
4
|. Докажите, что следующие утвержде
-
ния эквивалентны:
а) точки z
i
образуют прямоугольник,
б) справедливо равенство z
1
+ z
2
+ z
3
+ z
4
= 0,
в) числа z
i
являются корнями уравнения вида
(z
2
−a
2
)(z
2
−b
2
) = 0, |a|= |b|6= 0.
24. Пусть |z|= 1. Докажите, что
z − 1
a
=
|z − a|
|a|
.
25*. Решите в действительных и комплексных числах системы
x −
x −3y
x
2
+ y
2
= 2;
y +
3x + y
x
2
+ y
2
= 3;
x
2
−y
2
−
x + 3y
x
2
+ y
2
= 2;
2xy +
3x + y
x
2
+ y
2
= 3.
26. Можно в качестве основания позиционной системы счисления
выбирать даже комплексные числа, например, при выборе основания
b = 2i получается
«
мнимочетверичная
»
система. В качестве цифр в ней
используются 0, 1, 2, 3, и запись (a
n
, ..., a
0
, a
−1
, ..., a
−k
)
2i
означает
n
P
S=−k
a
S
· (2i)
S
.
Проверьте, что
(a
2n
... a
0
, a
−1
... a
−2k
)
2i
=
= (a
2n
... a
2
, a
−2
... a
−2k
)
−4
+ 2i(a
2n−1
... a
1
, a
−1
... a
−2k+1
)
−4
.
В этой системе любое комплексное число с двоично
-
рациональными
компонентами можно записать без знака и без разделения на действи
-
тельную и мнимую часть.
