Гашков С.Б. Современная элементарная алгебра в задачах и решениях
Подождите немного. Документ загружается.


§ 4.5. Корни из комплексных чисел 231
21*. (Мультипликативный вариант формулы обращения Мёбиуса.)
Докажите, что если при любом n
g(n) =
Y
d|n
f(d),
то
f(n) =
Y
d|n
g(n
/
d)
µ(n)
.
22*. Докажите, что
f
n
(x) =
Y
d|n
(x
d
−1)
µ(n
/
d)
.
23*. Докажите, что сумма первообразных корней n
-
й степени из 1
в поле C равна µ(n), а произведение их равно (−1)
ϕ(n)
, и, значит,
f
n
(x) = x
n
−µ(n)x
n−1
+ ... + 1.
24*. Докажите, что при простом p
f
p
(x) = x
p−1
+ x
p−2
+ ... + 1,
и этот многочлен неприводим над полем рациональных чисел.
25*. Докажите, что при простом p и k > 1
f
p
k
(x) = f
p
(x
p
k−1
) = x
(p−1) p
k−1
+ x
(p−2) p
k−1
+ ... + 1,
и этот многочлен неприводим над полем рациональных чисел.
26*. Докажите, что f
2n
(x) = f
n
(−x), если n нечетно.
27*. Докажите, что f
pn
(x) = f
n
(x
p
)
/
f
n
(x), если p простое и n не крат
-
но p.
28*. Докажите, что f
mn
(x) = f
n
(x
m
), если каждый простой делитель n
делит также m.
29**. Докажите, что любой круговой многочлен неприводим над по
-
лем рациональных чисел.
30*. (Быстрый алгоритм вычисления кругового многочлена f
n
(x).)
Находим все простые делители p
1
, ..., p
m
у числа n и вычисляем после
-
довательно многочлены по формулам
g
0
(x) = x −1, g
i
(x) = g
i−1
(x
p
i
)
/
g
i−1
(x), i = 1, . . ., m,
f
n
(x) = g
m
(x
n
/
(p
1
. . .p
m
)
).
Обоснуйте этот алгоритм.
31. Постройте из отрезков длины 1, 2, ..., 6 выпуклый равноугольный
шестиугольник.

232 Глава IV. Алгебраические уравнения
32*. Докажите, что из отрезков длины 1, 2, . .., n нельзя составить
выпуклый равноугольный n
-
угольник при n, равном степени простого,
и можно его построить во всех остальных случаях.
У к а з а н и е. Задача равносильна следующей: существует ли много
-
член f(x) = a
0
+ a
1
x + ... + a
n−1
x
n−1
, у которого коэффициенты являют
-
ся перестановкой последовательности 1, . .., n, такой, что f(ε
n
) = 0, где
ε
n
= e
2πi
/
n
? Примените задачи 24, 25 и 29.
Если (m, n) = 1, то
(1 + 2x + . .. + nx
n−1
)(1 + x
n
+ x
2n
+ ... + x
(m−1)n
) +
+ (nx + ... + n(m −1)x
m−1
)(1 + x
m
+ x
2m
+ ... + x
(n−1)m
) =
= a
0
+ a
1
x + .. . + a
mn−1
x
mn−1
,
где числа последовательности a
k
дают при делении на n и m разные па
-
ры остатков, так как остатки по модулю n повторяются с периодом n,
а остатки по модулю m повторяются с периодом m, и оба периода со
-
стоят из разных чисел, поэтому, согласно китайской теореме, все числа
последовательности a
k
будут разными по модулю mn, а значит, образуют
перестановку последовательности 1, ..., mn.
§ 4.6. Кубические уравнения над полем
комплексных чисел
Тригонометрическая форма записи комплексного числа позволяет
установить связь между решениями уравнения третьей степени из пре
-
дыдущих параграфов. Для этого вернемся к нашему уравнению
(u
3
)
2
+ Bu
3
−
A
3
27
= 0.
Пусть
∆ =
A
3
27
+
B
2
4
< 0.
Тогда
u
3
= −
B
2
±
p
|∆|i, v
3
= −
B
2
∓
p
|∆|i
––
сопряженные друг другу комплексные числа.
Нам нужно извлечь из них корень третьей степени.
Определение 100. Назовем корнем n-й степени из комплексного
числа z и обозначим
n
√
z множество всех комплексных чисел, при возве
-
дении в n
-
ю степень дающих z.

§ 4.6. Кубические уравнения над полем комплексных чисел 233
Из теоремы 97 следует, что этих чисел n штук и что они имеют сле
-
дующий вид:
n
p
|z|
cos
ϕ + 2kπ
n
+ i sin
ϕ + 2kπ
n
при k = 0, 1, ..., n −1.
В силу того, что u
−3
= (
¯
v)
−3
, можно считать, что числа u и v сопряже
-
ны. Значит, их сумма вещественна. Это означает, что мы получили три
вещественных решения уравнения x
3
+ Ax + B = 0 в виде
u + v =
3
r
−
B
2
+
√
∆ +
3
r
−
B
2
−
√
∆.
Упражнение 101. Выведите из этой формулы тригонометрическое
решение кубического уравнения.
Полученное выражение может иметь, вообще говоря, 36 значений:
каждый из двух радикалов
3
p
принимает по 3 значения и каждый из двух
радикалов
p
принимает по 2 значения. А нам нужны только три из них.
С квадратными радикалами справиться легко, так как извлекается ко
-
рень из одного и того же выражения ∆. Для этого условимся, что если
в некоторой формуле несколько раз встречается радикал из одного и то
-
го же выражения, то этому радикалу придается одно и то же значение.
Наше выражение u + v не меняется при одновременной смене знака у
√
∆
в двух местах. Поэтому остается лишь 9 значений для корней, зависящих
от выбора значений двух радикалов 3
-
й степени.
Для устранения этой трудности заметим, что второе уравнение систе
-
мы из предыдущего параграфа имеет вид uv = −
A
3
, т. е. произведение uv
всегда действительно. Выберем произвольное значение u
1
. Тогда из фор
-
мулы для произведения комплексных чисел в тригонометрической форме
следует, что все другие значения u
1
суть u
1
ρ и u
1
ρ
2
, где
ρ = cos
2π
3
+ i sin
2π
3
= −
1
2
+
√
3
2
i
(напомним, что ρ
3
= 1). Каждому значению u = u
1
, u
1
ρ, u
1
ρ
2
сопоставим
v = −
A
3u
. Тогда v принимает значения v
1
, v
1
ρ
2
, v
1
ρ.
В результате доказана
Теорема 98. Все вещественные корни уравнения
x
3
+ Ax + B = 0
при вещественных A и B находятся среди трех чисел:
x
1
= u
1
+ v
1
; x
2
= u
1
ρ + v
1
ρ; x
3
= u
1
ρ
2
+ v
1
ρ
2
, (3)

234 Глава IV. Алгебраические уравнения
где u
1
––
произвольное из значений корня
3
r
−
B
2
+
√
∆,
а v
1
= −
A
3u
1
.
Причем если ∆ > 0, то ровно одно из них вещественно, если
∆ < 0, то все три числа вещественны.
Сделаем теперь следующий шаг в обобщении: будем считать коэф
-
фициенты исходного уравнения комплексными числами. При решении
ничего по сути не меняется: мы приходим к системе, решая которую,
получаем формулу для корней кубического уравнения в радикалах. Три
корня определяем, как и выше: выбираем произвольно u
1
, потом берем
v
1
= −
A
3u
1
и выписываем формулы (3).
Тогда получаем комплексный вариант формулы Кардано:
Теорема 99. Все корни уравнения
x
3
+ Ax + B = 0
при произвольных комплексных A и B задаются формулами
x
1
= u
1
+ v
1
, x
2
= u
1
ρ + v
1
ρ, x
3
= u
1
ρ
2
+ v
1
ρ
2
,
где u
1
––
произвольное из значений корня
3
r
−
B
2
+
√
∆,
а v
1
= −
A
3u
1
.
Легко видеть из формул для решения кубического уравнения, что
∆ = 0 тогда и только тогда, когда у исходного уравнения есть кратные
корни.
В дальнейшем, если не оговорено противное, мы будем считать коэф
-
фициенты алгебраических уравнений комплексными числами.
Задачи и упражнения к § 4.6
1. Докажите, что при решении уравнений с рациональными коэффи
-
циентами по формуле Кардано все корни в формуле извлекаются тогда
и только тогда, когда решения уравнения имеют вид 2a, −a ∓bi
√
3 при
рациональных a и b.

§ 4.7. Уравнения четвертой степени 235
2. Докажите, что
3
√
a + bi =
u(a + bi) + u
2
i
2a
3
p
a
2
+ b
2
,
где u
––
корень уравнения u
3
−3(a
2
+ b
2
)u −2b(a
2
+ b
2
) = 0.
3. Решите по формуле Кардано уравнения:
а) x
3
−6x + 9 = 0; д) x
3
+ 6x + 2 = 0;
б) x
3
+ 12x + 63 = 0; е) x
3
+ 3x
2
−6x + 4 = 0;
в) x
3
+ 9x
2
+ 18x + 28 = 0; ж) x
3
+ 3x −2i = 0;
г) x
3
+ 6x
2
+ 30x + 25 = 0; з) x
3
−3ax + a
3
+ 1 = 0.
4. Если все корни уравнения z
3
+ az
2
+ bz + c = 0 по модулю рав
-
ны 1, то модули a и b равны.
§ 4.7. Уравнения четвертой степени
Общее уравнение четвертой степени имеет вид:
x
4
+ ax
3
+ bx
2
+ cx + d = 0.
Как и раньше, уничтожим коэффициент a, выделяя полную четвертую
степень. Для этого сделаем замену переменной x
′
= x + a
/
4.
Упражнение 102. Проверьте, что после этой замены уравнение при
-
мет вид x
4
+ Ax
2
+ Bx + C = 0.
Попробуем разложить его в произведение двух квадратных уравнений:
x
4
+ Ax
2
+ Bx + C = (x
2
+ u
1
x + v
1
)(x
2
+ u
2
x + v
2
).
Раскрывая скобки и приравнивая коэффициенты, получаем систему
u
1
+ u
2
= 0;
v
1
+ v
2
+ u
1
u
2
= A;
u
1
v
2
+ u
2
v
1
= B;
v
1
v
2
= C.
Заменяя u
2
на −u
1
= −u, приходим к системе с тремя неизвестными:
v
1
+ v
2
= A + u
2
;
u(v
2
−v
1
) = B;
v
1
v
2
= C,
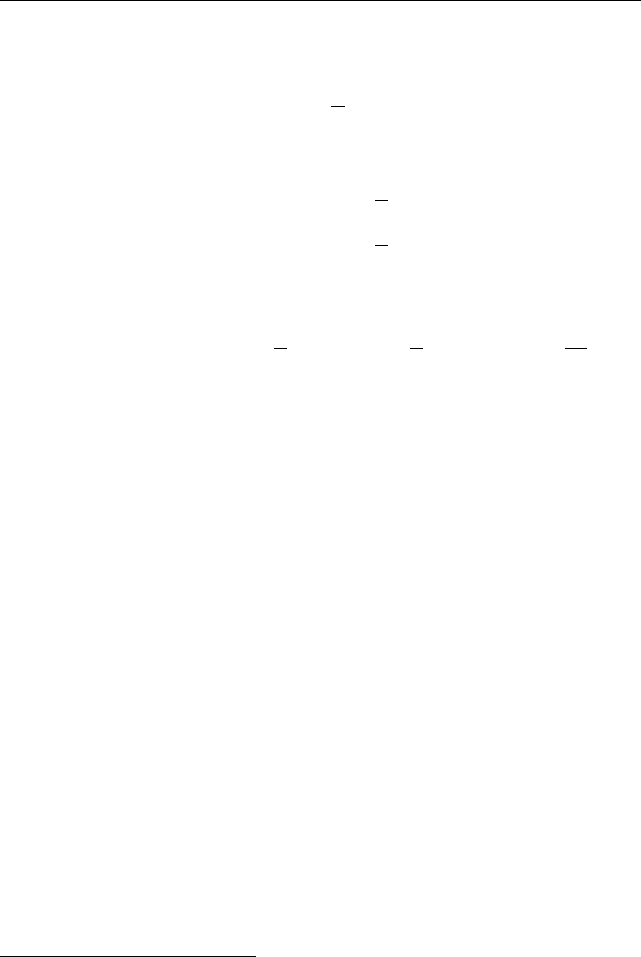
236 Глава IV. Алгебраические уравнения
которая равносильна системе
v
1
+ v
2
= A + u
2
;
v
2
−v
1
=
B
u
;
v
1
v
2
= C,
а последняя
––
системе
2v
2
= A + u
2
+
B
u
;
2v
1
= A + u
2
−
B
u
;
4v
1
v
2
= 4C.
Отсюда имеем
4C = 4v
1
v
2
=
(A + u
2
) +
B
u
(A + u
2
) −
B
u
= (A + u
2
)
2
−
B
2
u
2
,
или
u
6
+ 2Au
4
+ (A
2
−4C)u
2
−B
2
= 0.
Решив это кубическое относительно u
2
уравнение, называемое резоль-
вентой Феррари *, найдем решения системы. После этого, решив два
квадратных уравнения, получим решения уравнения 4
-
й степени.
Задачи и упражнения к § 4.7
1. Выразите через корни уравнения четвертой степени корни его ре
-
зольвенты Феррари.
2. Решите уравнения
а) x
4
−2x
3
+ 2x
2
+ 4x −8 = 0; д) x
4
−3x
3
+ x
2
+ 4x −6 = 0;
б) x
4
+ 2x
3
−2x
2
+ 6x −15 = 0; е) x
4
−2x
3
+ 4x
2
−2x + 3 = 0;
в) x
4
−x
3
−x
2
+ 2x −2 = 0; ж)* 4x
4
+ 12x
2
+ 16x −3 = 0;
г) x
4
−4x
3
+ 3x
2
+ 2x −1 = 0; з)* 4x
4
+ 4x + 3 = 0.
§ 4.8. Решение кубического уравнения
методом Лагранжа
Приведенные выше решения уравнений 2, 3 и 4
-
й степени оставляют
чувство неудовлетворенности. Создается впечатление, что они найдены
при помощи искусственных, не обобщаемых на высшие степени, прие
-
мов. В какой
-
то мере это действительно так. Однако можно предложить
* Л. Феррари (Lodovico Ferrari, 1522
–
1565)
––
итальянский математик, ученик Кардано,
первым решивший уравнение четвертой степени.

§ 4.8. Решение кубического уравнения методом Лагранжа 237
систематичный метод решения уравнений третьей и четвертой степеней.
Он основан на изучении свойств многочленов от корней исходного урав
-
нения в зависимости от перестановок корней.
Пусть x
1
, ..., x
n
––
все корни уравнения
x
n
+ a
1
x
n−1
+ ... + a
n
= 0.
Упражнение 103. Вспомните, как доказываются формулы Виета
(здесь мы уже можем считать, что корни уравнения
––
произвольные ком
-
плексные числа)
a
1
= −x
1
+ ... + x
n
;
a
2
= x
1
x
2
+ ... x
n−1
x
n
;
. . . . . . . . . . . . . . . . . . . . . .
a
n
= (−1)
n
x
1
... x
n
.
Упражнение 104. Вспомните, как решается система
(
u + v = a;
uv = b.
Лагранж предложил следующий метод нахождения корней x
1
, x
2
, x
3
уравнения x
3
+ ax + b = 0.
Прежде всего заметим, что сумма x
1
+ x
2
+ x
3
равна нулю (так как она
отличается от коэффициента при x
2
исходного уравнения лишь знаком).
Пусть ρ = −
1
2
+
√
−3
2
––
корень третьей степени из единицы.
Упражнение 105. Проверьте, что 1 + ρ + ρ
2
= 0.
Напишем еще две суммы:
(ρ, x) = x
1
+ ρx
2
+ ρ
2
x
3
и (ρ, x) = x
1
+ ρ
2
x
2
+ ρx
3
.
Заметим, что, циклически переставляя переменные в них, получим про
-
порциональные им выражения:
x
2
+ ρx
3
+ ρ
2
x
1
= ρ
2
(ρ, x), x
2
+ ρx
1
+ ρ
2
x
3
= ρ(ρ
2
, x) и т. д.
Кроме того, меняя местами пару переменных одной из сумм в (ρ, x)
и (ρ
2
, x), получим выражение, пропорциональное другой сумме:
x
2
+ ρx
1
+ ρ
2
x
3
= ρ(ρ
2
, x), x
2
+ ρ
2
x
1
+ ρx
3
= ρ
2
(ρ, x) и т. д.
При указанных заменах переменных коэффициенты пропорциональности
всегда суть корни третьей степени из единицы, так что при возведении
в куб они равны единице. Поэтому выражение (ρ, x)
3
+ (ρ
2
, x)
3
не меня
-
ется при перестановках переменных.

238 Глава IV. Алгебраические уравнения
Отметим, что коэффициенты пропорциональности у выражений (ρ, x)
и (ρ
2
, x) при одной и той же перестановке переменных взаимно обратны.
Поэтому выражение (ρ, x) · (ρ
2
, x) также не меняется при заменах пере
-
менных.
Выразим их через коэффициенты a и b. Прежде всего заметим, что
(ρ, x)
3
+ (ρ
2
, x)
3
= ((ρ, x) + (ρ
2
, x))(((ρ, x) + (ρ
2
, x))
2
−3(ρ, x) (ρ
2
, x)),
(ρ, x) + (ρ
2
, x) = (x
1
+ ρx
2
+ ρ
2
x
3
) + (x
1
+ ρ
2
x
2
+ ρx
3
) =
= 2x
1
+ (ρ + ρ
2
)(x
2
+ x
3
) = 2x
1
− (x
2
+ x
3
) =
= 3x
1
− (x
1
+ x
2
+ x
3
) = 3x
1
−0 = 3x
1
(так как ρ + ρ
2
= −1) и
(ρ, x) (ρ
2
, x) = (x
1
+ ρx
2
+ ρ
2
x
3
)(x
1
+ ρ
2
x
2
+ ρx
3
) = x
2
1
+ x
2
2
+ x
2
3
+
+ (ρ + ρ
2
)(x
1
x
2
+ x
2
x
3
+ x
3
x
1
) = x
1
+ x
2
+ x
3
− (x
1
x
2
+ x
2
x
3
+ x
3
x
1
) =
= (x
1
+ x
2
+ x
3
)
2
−3(x
1
x
2
+ x
2
x
3
+ x
3
x
1
) = 0 −3a = −3a
(так как x
1
+ x
2
+ x
3
= 0).
Поэтому
(ρ, x)
3
+ (ρ
2
, x)
3
= 3x
1
(9x
2
1
+ 9a) = 27(x
3
1
+ ax
1
).
Однако x
1
––
корень исходного уравнения, значит, x
3
1
+ ax
1
+ b = 0,
откуда x
3
1
+ ax
1
= −b.
Поэтому в результате получаем, что
(
(ρ, x)
3
+ (ρ
2
, x)
3
= −27b;
(ρ, x) · (ρ
2
, x) = −3a.
Полученная система легко решается относительно неизвестных (ρ, x)
и (ρ
2
, x). Действительно,
(ρ
2
, x) =
−3a
(ρ, x)
,
поэтому
(ρ, x)
6
+ 27b(ρ, x)
3
−27a
3
= 0,
значит,
(ρ, x)
3
= 27
−
b
2
+
√
∆
;
(ρ
2
, x)
3
= 27
−
b
2
−
√
∆
,
(4)
где
∆ =
a
3
27
+
b
2
4
,
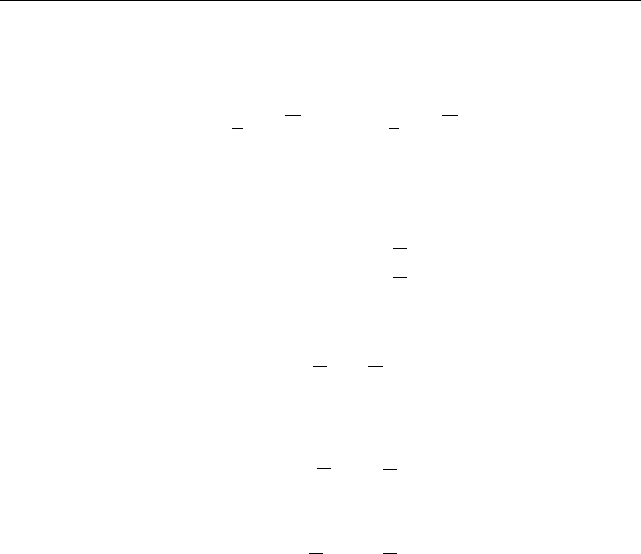
§ 4.8. Решение кубического уравнения методом Лагранжа 239
или
(
(ρ, x)
3
= 27A;
(ρ
2
, x)
3
= 27B,
где
A = −
b
2
+
√
∆, B = −
b
2
−
√
∆.
Выразим x
1
, x
2
, x
3
из (ρ, x) и (ρ
2
, x), последовательно исключая неиз
-
вестные из системы:
x
1
+ x
2
+ x
3
= 0;
x
1
+ ρx + ρ
2
x = 3
3
√
A;
x
1
+ ρ
2
x + ρx = 3
3
√
B.
Складывая все три уравнения с учетом равенства 1 + ρ + ρ
2
= 0 и сокра
-
щая тройку, находим
x
1
=
3
√
A +
3
√
B.
Аналогично, умножая второе уравнение на ρ
2
, третье на ρ и складывая
их с первым, после сокращения на три находим
x
2
= ρ
2
3
√
A + ρ
3
√
B.
А умножая второе уравнение на ρ, третье на ρ
2
и складывая их с пер
-
вым, имеем
x
3
= ρ
3
√
A + ρ
2
3
√
B.
В результате мы получили формулы Кардано (3) из теоремы 98 с точ
-
ностью до порядка следования x
1
, x
2
, x
3
.
Из этих формул вытекает выражение
((ρ, x)
3
− (ρ
2
, x)
3
)
2
= ((ρ, x)
3
+ (ρ
2
, x)
3
)
2
−4(ρ, x)
3
(ρ
2
, x)
3
=
= (−27b)
2
+ 4(27a
3
) = 27(4a
3
+ 27b
2
) = 27 ·108∆.
Упражнение 106. Выведите из предыдущего равенства, что
108∆ = (x
2
−x
1
)
2
(x
3
−x
2
)
2
(x
3
−x
1
)
2
,
используя равенства
u
3
−v
3
= (u −v) (u −ρv) (u −ρ
2
v), (1 − ρ)(1 −ρ
2
) = 3.
Определение 101. Выражение
D = (x
2
−x
1
)
2
(x
3
−x
2
)
2
(x
3
−x
1
)
2
называют дискриминантом кубического уравнения.

240 Глава IV. Алгебраические уравнения
Вообще, дискриминантом уравнения n-й степени
x
n
+ a
n−1
x
n−1
+ ... + a
1
x + a
0
= 0
называют симметрический многочлен от корней x
1
, x
2
, . .., x
n
этого урав
-
нения D =
Q
i> j
(x
i
−x
j
)
2
.
Задачи и упражнения к § 4.8
1. Выразить дискриминант D через коэффициенты для общего урав
-
нения третьей и четвертой степени.
2. Решите общее уравнение третьей степени в случае нулевого дис
-
криминанта.
3*. Решите уравнение
(x
3
−3qx + p
3
−3pq)
2
−4(px + q)
3
= 0.
У к а з а н и е. Рассмотрите уравнение относительно z
z
3
− (3px + q)z + x
3
−3qx + p
3
−3pq = 0
с нулевым дискриминантом и вынесите в нем за скобки множитель
z + x + p.
4. Решите уравнения:
а) (x
2
+ 3)
/
(x + 3)
3
= 26
/
343; б) x
6
+ 1 = 0; в) (x
2
+ x)
4
= 1.
5. Числа a, b, c
––
три из четырех корней многочлена x
4
−ax
3
−bx +c.
Найдите эти числа.
6. Найдите все p и q, при которых четыре корня многочлена
x
4
+ px
2
+ q действительны и образуют арифметическую прогрессию.
§ 4.9. Решение методом Лагранжа уравнений
четвертой степени
Попытаемся обобщить метод предыдущего параграфа на случай 4
-
й
степени. Рассмотрим выражение
t(x
1
, x
2
, x
3
, x
4
) = x
1
+ αx
2
+ α
2
x
3
+ α
3
x
4
,
где α = i
––
корень 4
-
й степени из 1, а x
1
, ..., x
4
––
корни уравнения
x
4
+ ax
2
+ bx + c = 0, то есть
t = x
1
−x
3
+ (x
2
−x
4
)i.
Сколько значений принимает выражение t при различных переста
-
новках корней? Очевидно, 24 значения
––
столько же, сколько всех воз
-
можных перестановок.
